[논문리뷰] Quadratic Gaussian Splatting: High Quality Surface Reconstruction with Second-order Geometric Primitives
ICCV 2025. [Paper] [Page] [Github]
Ziyu Zhang, Binbin Huang, Hanqing Jiang, Liyang Zhou, Xiaojun Xiang, Shunhan Shen
CASIA | UCAS | The University of Hong Kong | SenseTime Research
25 Nov 2024
Introduction
본 논문에서는 3DGS의 타원체 표현과 2DGS의 타원 원반 표현을 보다 일반적인 quadratic 프레임워크로 확장하였다. 구체적으로, implicit function $f(x, y, z) = 0$을 사용하여 primitive 경계를 정의한다. 여기서 $f(x, y, z) < 0$은 primitive 경계 내부의 점에 해당하고, $f(x, y, z) > 0$은 경계 외부의 점에 해당한다. Quadratic form
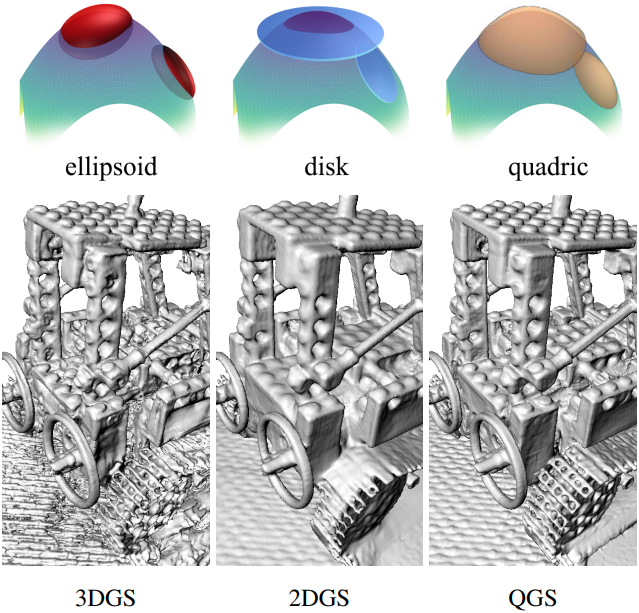
\[\begin{equation} f(x, y, z) = (x, y, z, 1)^\top \textbf{Q} (x, y, z, 1) = 0 \end{equation}\]을 채택하였으며, $\textbf{Q} \in \mathbb{R}^{4 \times 4}$는 conic matrix이고, 원기둥, 타원체, 포물면, 쌍곡면을 포함한 다양한 도형을 표현할 수 있다. 결과적으로, 3D Gaussian primitive를 일반화하고 2DGS를 특수한 경우로 포함하여 고차 표면 적응을 가능하게 한다. 특히, splatting 맥락에서 이 표현을 실용적이고 다재다능하게 만드는 효율적인 ray-quadratic 교차 알고리즘이 있다. Primitive가 본질적으로 second-order primitive이므로, 본 방법을 Quadratic Gaussian Splatting (QGS)이라고 한다.
그러나 변형 가능한 quadratic primitive의 경우, 연속적인 밀도 분포를 정의하는 것이 핵심 과제이다. 변형 가능한 quadratic 표면은 기하 구조를 고려한 density metric을 필요로 한다. 예를 들어, primitive가 원반에서 포물면으로 변형될 때, 유클리드 거리는 곡면을 무시하는 직선 거리를 측정한다. Geodesic distance는 표면을 따라가기 때문에 더 정확한 밀도 모델링을 제공하지만, 일반적으로 계산하기가 어렵다.
다행히 표면 모델링을 목표로 하기 때문에, 효율적인 closed-form geodesic solver가 존재하는 포물면으로 quadratic 표현을 제한한다. 이를 통해 포인트 기반 렌더링 효율성을 유지하는 동시에 적응형 곡률 모델링을 가능하게 한다. 하나의 포물면이 여러 평면 surfel을 필요로 하는 복잡한 기하 구조를 근사하여 유사한 primitive 수로 더 높은 충실도를 달성한다. 저자들은 2DGS에서 영감을 받아, splatting을 위한 ray-splat 교차점을 채택하여 멀티뷰 일관성과 원근 정확성을 유지하였다. Surfel의 특성 덕분에 QGS는 원근 왜곡 및 popping 효과를 해결하는 고급 splatting 기법이나, 추가적인 계산 비용이 발생하더라도 전반적인 기하 구조 정확도를 향상시키는 고급 표면 정규화를 활용할 수 있다.
QGS는 SOTA 표면 재구성 정확도를 달성하였으며, 2DGS보다 기하학적 정확도가 33% 향상되었다.
Method
1. Quadratic Gaussian Splatting
Quadratic Gaussian Model
Homogeneous coordinate $\textbf{x} = [x, y, z, 1]^\top \in \mathbb{R}^4$가 주어지면, 2차 곡면은 다음 방정식의 해 집합으로 정의될 수 있다.
저자들은 object space에서 parameter space로의 변환을 얻기 위해 congruent transformation을 적용하였다.
\[\begin{equation} \textbf{Q} = \textbf{T}^{-\top} \textbf{D} \textbf{T}^{-1}, \quad \textrm{with} \; \textbf{D} \; \textrm{symmetrical}, \; \textbf{T} = \begin{bmatrix} \textbf{R} & \textbf{c} \\ 0 & 1 \end{bmatrix} \end{equation}\]$\textbf{c}$는 2차 곡면의 위치이고, \(\textbf{R} = [\textbf{r}_1, \textbf{r}_2, \textbf{r}_3]\)는 object space에서의 orientation이며, \(\textbf{D}\)는 표면의 scale과 모양을 결정한다. 예를 들어, $\textbf{D} = \textrm{diag}(s_1^2, s_2^2, s_3^2, 1)$이면 타원체이고, $\textbf{D} = \textrm{diag}(s_1^2, s_2^2, 0, 0)$은 평면이다.

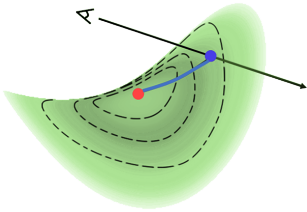
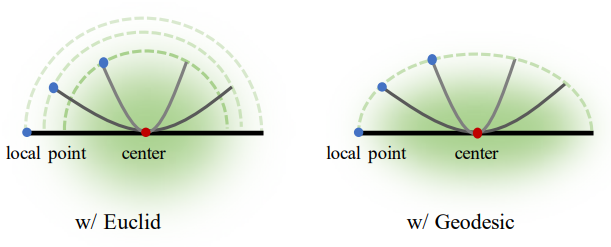
임의의 표면 지점에서 Gaussian 가중치를 계산하기 위해 먼저 표면에서 Gaussian 분포를 확립하기 위한 metric을 정의한다. 간단한 방법은 유클리드 거리를 사용하여 Gaussian 분포를 구성하는 것이다. 그러나 이 방법은 표면이 변형될 때 불일치를 초래하여 위 그림과 같이 불균일한 splatting 재구성 아티팩트가 발생한다. 이 문제를 해결하기 위해 geodesic distance를 사용하여 가중치가 표면 변형에 일관되게 적용되도록 한다. 아래 그림은 1차원 예시이다.
그러나 모든 geodesic이 closed-form solution을 가지지는 않는다. $\textbf{Q}$가 타원체 또는 쌍곡면일 때, geodesic distance를 계산하려면 일반적으로 수치적 방법이 필요한다. 본 논문에서는 표면 재구성을 목표로 하기 때문에 다음과 같은 형태의 포물면에 초점을 맞추었다.
$\hat{\cdot}$은 Gaussian 로컬 좌표를 뜻한다. \(d_{ii} \in \{0, \pm 1\}\)은 포물면이 타원, 쌍곡선 또는 평면 포물면인지를 결정한다. 그러나 $d_{ii}$는 discrete하므로, primitive는 타원 포물면과 쌍곡선 포물면 사이를 부드럽게 전환할 수 없다. 이 문제를 해결하기 위해, 포물면 유형 간의 미분 가능한 전환에 대한 부호 있는 scale을 도입한다.
\[\begin{equation} f(\hat{x}, \hat{y}, \hat{z}) = \frac{\textrm{sign}(s_1)}{s_1^2} \hat{x}^2 + \frac{\textrm{sign}(s_2)}{s_2^2} \hat{y}^2 - \frac{1}{s_3} \hat{z} = 0 \end{equation}\]3DGS에서는 exp activation function을 통해 scale을 구하였다. 부호를 추가하기 위해, 부호를 제어하는 또 다른 변수 $t$를 추가한다.
\[\begin{equation} s(x, t) = \textrm{tanh}(t) \exp(x) \end{equation}\]Gaussian Distribution on Quadric
포물면은 다음과 같이 명시적으로 표현할 수 있다.
\[\begin{equation} \hat{z} (\hat{x}, \hat{y}) = s_3 \left( \frac{\textrm{sign}(s_1)}{s_1^2} \hat{x}^2 + \frac{\textrm{sign}(s_2)}{s_2^2} \hat{y}^2 \right) \end{equation}\]이를 원통 좌표계로 만든다. 즉, $\hat{x} = \rho \textrm{cos}(\theta)$, $\hat{y} = \rho \textrm{sin}(\theta)$이다.
\[\begin{equation} \hat{z} (\theta, \rho) = s_3 \left( \frac{\textrm{sign}(s_1) \textrm{cos}^2 \theta}{s_1^2} + \frac{\textrm{sign}(s_2) \textrm{sin}^2 \theta}{s_2^2} \right) \rho^2 = a(\theta) \rho^2 \end{equation}\]포물면의 대칭성으로 인해, 임의의 점 \(\hat{\textbf{p}}_0 = (\rho_0, \theta_0, \hat{z}(\theta_0, \rho_0))\)에 대해, 평면 \(\theta = \theta_0\)와 포물면의 교선 \(\hat{z}(\theta_0, \rho), \rho \in (0, \rho_0)\)는 원점에 대한 geodesic이다. 따라서 geodesic distance는 이 곡선의 호 길이 $l$과 같다.
\[\begin{equation} l(a, \rho_0) = \int_0^{\rho_0} \sqrt{1 + (2at)^2} \textrm{d}t = \frac{\ln (\sqrt{u^2 + 1} + u) + u \sqrt{u^2 + 1}}{4a} \\ \textrm{where} \; u = 2a \rho_0 \end{equation}\]그런 다음, 2차 곡면의 원점에 있는 곡면에서 2D Gaussian 분포의 평균을 정의한다. 여기서 $(s_1, s_2)$는 Gaussian 분포의 주축 분산을 나타낸다. 2D Gaussian 분포의 등고선은 타원을 형성하므로 다음과 같이 쓸 수 있다.
\[\begin{equation} \frac{\rho^2 \textrm{cos}^2 \theta}{s_1^2} + \frac{\rho^2 \textrm{sin}^2 \theta}{s_2^2} = 1 \end{equation}\]타원 위의 점 \((\theta_0, \rho_0)\)가 주어졌을 때, \(\rho_0\)는 \(\theta_0\) 방향의 2D Gaussian 분포의 표준편차를 나타낸다.
\[\begin{equation} \sigma (\theta_0) = \rho_0 = \frac{s_1 s_2}{\sqrt{(s_2 \textrm{cos} \theta_0)^2 + (s_1 \textrm{sin} \theta_0)^2}} \end{equation}\]따라서 표면의 모든 점 \(\hat{\textbf{p}}_0\)에 대해 다음과 같이 해당 Gaussian 함수 값을 정의할 수 있다.
\[\begin{equation} G (\hat{\textbf{p}}_0 (\theta_0, \rho_0)) = \exp \left( - \frac{(l(a(\theta_0), \rho_0))^2}{2 (\sigma (\theta_0))^2} \right) \end{equation}\]특히, $\vert s_3 \vert \rightarrow 0$일 때 포물면은 원반이 된다. 또한, $x \rightarrow 0$일 때 $\sqrt{1+x} \rightarrow 1$이고 $\ln(1 + x) \sim x$가 되므로, $\vert s_3 \vert \rightarrow 0$일 때 $a \rightarrow 0$과 \(l \rightarrow \rho_0\)가 된다. 이는 geodesic distance가 유클리드 거리와 동치함을 의미한다. 이는 2DGS가 QGS의 특정 케이스로 간주될 수 있음을 시사하며, 더 일반화된 특성 덕분에 고곡률 영역에 효과적으로 fitting할 수 있다.
Splatting
Ray-splat Intersection
Gaussian 로컬 좌표계에서 카메라 중심을 \(\hat{\textbf{o}} \in \mathbb{R}^{3 \times 1}\), 광선 방향을 \(\hat{\textbf{d}} \in \mathbb{R}^{3 \times 1}\)라 하자. 광선 위의 점은
\[\begin{equation} \hat{\textbf{p}} = \hat{\textbf{o}} + t \hat{\textbf{d}} \end{equation}\]로 정의할 수 있다. $\hat{\textbf{p}}$를 $\hat{z} (\hat{x}, \hat{y})$ 식에 대입하여 2차 방정식을 풀어 두 개의 교차점을 얻을 수 있다. 가까운 점을 \(\hat{\textbf{p}}_n = (\hat{x}_n, \hat{y}_n, \hat{z}_n)\), 먼 점을 \(\hat{\textbf{p}}_f = (\hat{x}_f, \hat{y}_f, \hat{z}_f)\)라 하자 $(t_n \le t_f)$.
QGS에서 멀티뷰 일관성을 보장하기 위해 두 개의 유효한 점 중 하나만 선택한다. 먼저 pˆn의 geodesic distance가 \(3 \sigma (\theta_n)\) 이내에 있으면 \(\hat{\textbf{p}}_n\)을 선택한다. 그렇지 않으면 \(\hat{\textbf{p}}_f\)가 \(3 \sigma (\theta_f)\) 이내에 있는지 확인하고, 이내에 있으면 \(\hat{\textbf{p}}_f\)를 선택한다. 두 조건 모두 충족되지 않으면, 광선과 primitive 사이에 교점이 없다고 가정한다. 이 가정은 일반적으로 유효한데, 유의미한 가중치로 인해 첫 번째 점이 두 번째 점을 가리는 경우가 많기 때문이다.
Normal and Curvature
2DGS와 유사하게, QGS는 표면 기반 표현으로, 본질적으로 멀티뷰 일관성을 갖는 기하학적 속성을 가지므로 표면 normal을 계산하기 쉽다. 표면 상의 임의의 점 \(\hat{\textbf{p}}_0 = (\hat{x}_0, \hat{y}_0, \hat{z}(\hat{x}_0, \hat{y}_0))\)가 주어지면, $f(\hat{x}, \hat{y}, \hat{z})$의 편미분을 구하여 다음을 얻을 수 있다.
\[\begin{equation} \hat{\textbf{n}}_0 (\hat{\textbf{p}}_0) = \left( \frac{2 \textrm{sign}(s_1)}{s_1^2} \hat{x}_0, \frac{2 \textrm{sign}(s_2)}{s_2^2} \hat{y}_0, - \frac{1}{s_3} \right) \end{equation}\]QGS는 curvature와 같은 2차 기하 정보를 자연스럽게 출력한다. 각 QGS primitive에 대해 ray-splat 교차점의 Gaussian curvature를 계산할 수 있으며, 점 \(\hat{\textbf{p}}_0\)에서의 curvature는 다음과 같다.
\[\begin{equation} \hat{K}_0 (\hat{\textbf{p}}_0) = \frac{4 \lambda_1 \lambda_2}{(1 + 4 \lambda_1^2 \hat{x}_0^2 + 4 \lambda_2 \hat{y}_0^2)^2} \\ \textrm{where} \quad \lambda_1 = \frac{\textrm{sign}(s_1) \cdot s_3}{s_1^2}, \; \lambda_2 = \frac{\textrm{sign}(s_2) \cdot s_3}{s_2^2} \end{equation}\]알파 블렌딩을 사용하여 주어진 시점에 대한 normal map $\textbf{N}$과 curvature map $\textbf{K}$를 렌더링한다.
\[\begin{equation} \{ \textbf{N}, \textbf{K} \} = \sum_{i=0}^{N-1} G_i \alpha_i \prod_{j=0}^{i-1} (1 - G_j \alpha_j) \{\textbf{n}_i, K_i\} \end{equation}\]
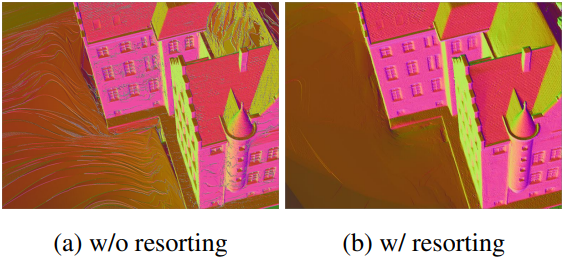
Per-pixel Resorting
저자들은 popping 아티팩트를 해결하기 위해 StopThePop의 픽셀별 재정렬 방법을 채택했다.
2. Optimization
Depth Distortion
저자들은 2DGS가 제안한 depth distortion loss와 normal consistency loss를 채택하였다.
\[\begin{equation} \mathcal{L}_d = \sum_{i=0}^{N-1} \sum_{j=0}^{i-1} \omega_i \omega_j (t_i - t_j)^2 \end{equation}\](\(\omega_i = \bar{\alpha}_i T_i\)는 $i$번째 Gaussian의 알파 블렌딩 가중치, $t_i$는 ray-splat 교차점의 깊이)
Curvature Guided Normal Consistency
2DGS는 normal consistency loss로 광선의 모든 primitive가 실제 표면과 로컬하게 정렬되도록 한다.
\[\begin{equation} \mathcal{L}_n = \sum_i \omega_i (1 - \textbf{n}_i^\top \textbf{N}) \end{equation}\]\(\textbf{n}_i\)는 카메라를 향한 splat normal, $\textbf{N}$은 depth point $\textbf{p}$를 인접 픽셀과 미분하여 계산한 normal)
그러나 인접 픽셀은 특히 edge 영역에서 로컬 평면 가정을 위반할 수 있다. Edge 영역에서 normal consistency loss를 사용하면 오차가 발생하여 2DGS에서 관찰되는 over-smoothing에 기여할 수 있다. 간단한 접근 방식은 이미지 edge를 사용하여 기하학적 edge를 근사하는 것이지만, 대부분의 장면에서 이미지 edge가 기하학적 edge와 완전히 일치하지 않는다. 특히 조명이 균일한 영역에서 그렇다.
따라서 curvature map을 사용하여 normal loss에 가중치를 부여한다.
\[\begin{equation} \lambda_K (K (u,v)) = 1 - \textrm{sigmoid} (\ln \vert K (u,v) \vert + \epsilon) \\ \mathcal{L}_\textrm{Kn} (u,v) = \lambda_K (K (u,v)) \mathcal{L}_n (u, v) \end{equation}\]Multi-view regularization Loss
평면 기반 PGSR과 더 공정한 비교를 보장하기 위해, PGSR의 멀티뷰 정규화를 통합하고 homography transformation을 통해 photometric consistency loss를 계산한다.
\[\begin{aligned} \textbf{H}_{rn} &= \textbf{K}_n (\textbf{R}_{rn} + \frac{\textbf{T}_{rn} \textbf{n}_r^\top}{\textbf{n}_r^\top \textbf{X}_r}) \textbf{K}_r^{-1} \\ \mathcal{L}_\textrm{Mv} &= \frac{1}{V} \sum_{\textbf{p}_r \in V} \| \textbf{p}_r - \textbf{H}_{nr} \textbf{H}_{rn} \textbf{p}_r \| \\ &+ (1 - \textrm{NCC}(\textbf{I}_r (\textbf{p}_r), \textbf{I}_n (\textbf{H}_{rn} \textbf{p}_r))) \end{aligned}\](\(\textbf{n}_r\)은 normal map, \(\textbf{X}_r\)은 depth map에서 얻은 3D 포인트들, \(\textbf{R}_{rn}\)은 relative rotation, $\textbf{K}$는 intrinsic, \(\textbf{p}_r\)은 픽셀 좌표, $\textbf{I}$는 이미지 intensity)
이 loss는 depth map과 normal map에서 reprojection error를 계산하고 normalized cross-correlation (NCC)을 적용하여 멀티뷰 제약 조건을 적용한다.
Final Loss
최종 loss는 다음과 같다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_c + \lambda_d \mathcal{L}_d + \lambda_n \mathcal{L}_\textrm{Kn} + \lambda_\textrm{Mv} \mathcal{L}_\textrm{Mv} \end{equation}\]Experiment
1. Comparison
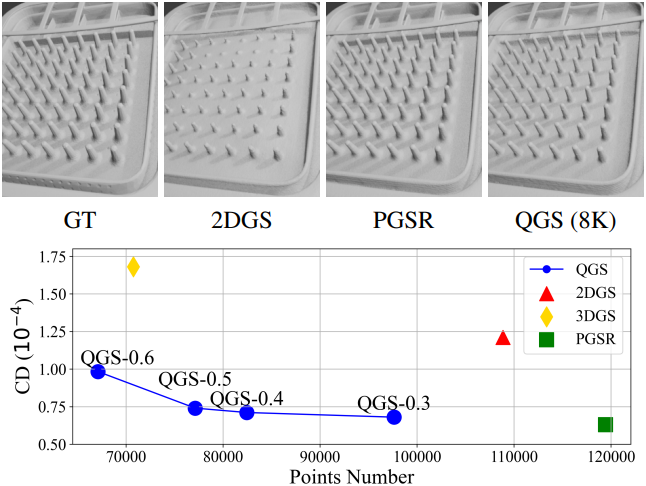
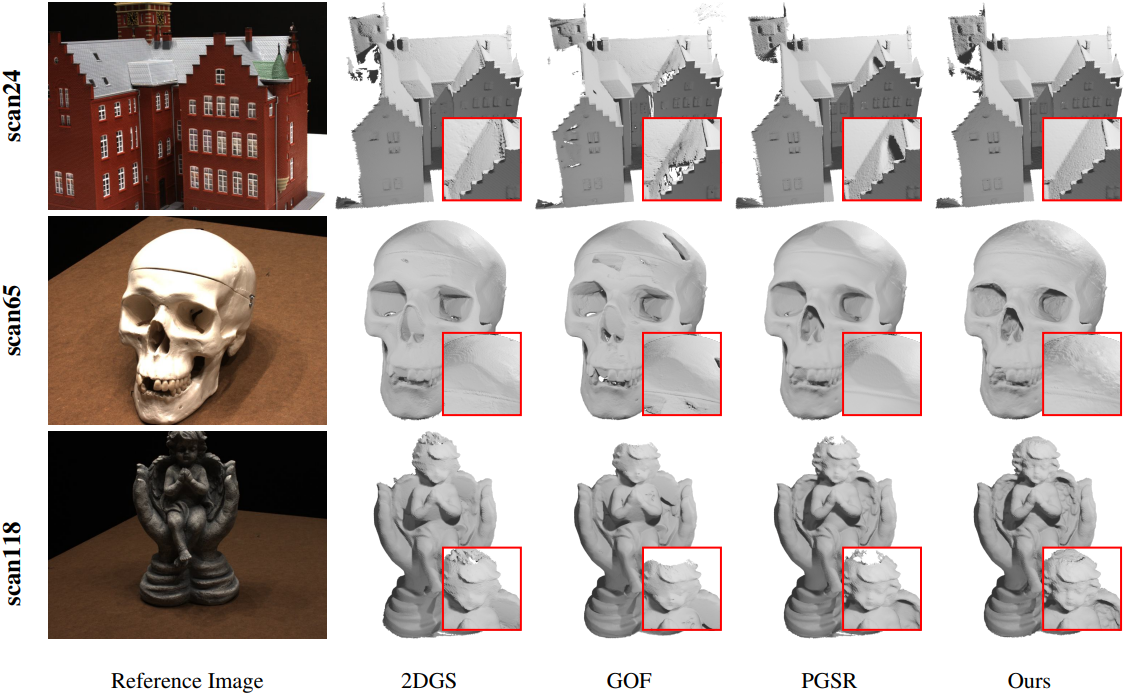
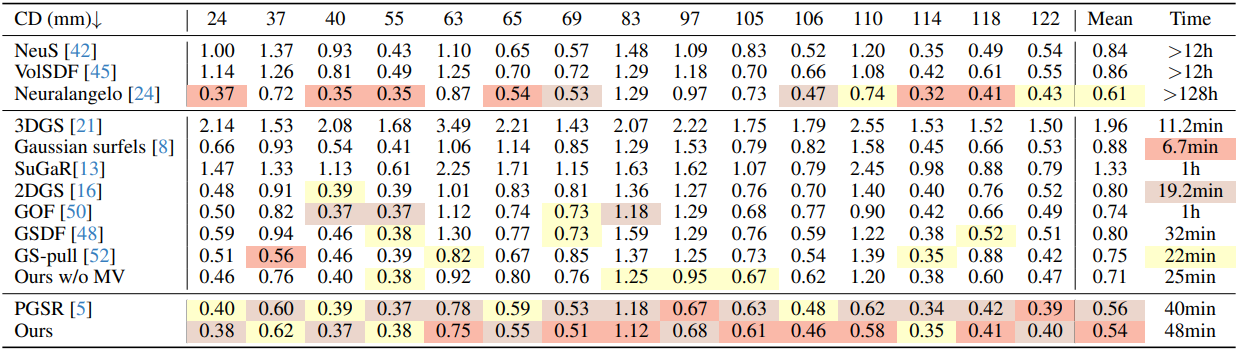
다음은 DTU 데이터셋에서의 비교 결과이다.
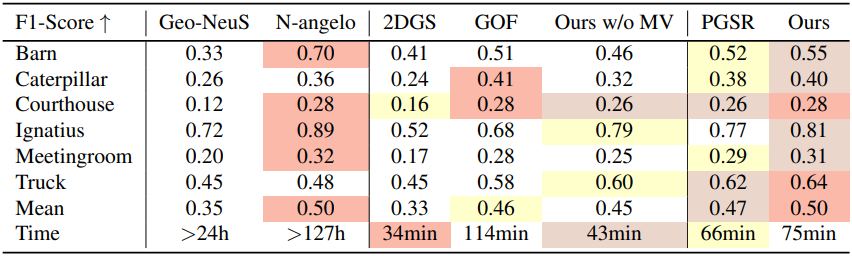
다음은 TNT 데이터셋에서의 비교 결과이다.

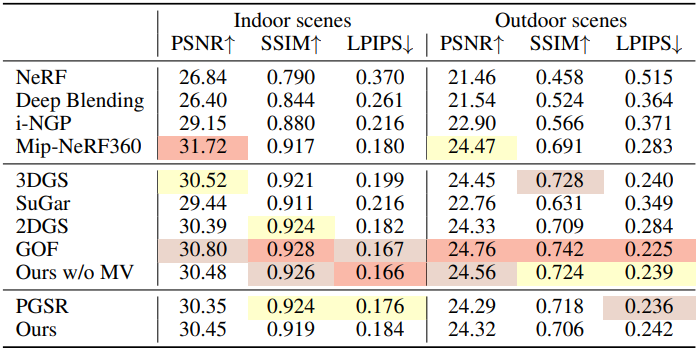
다음은 Mip-NeRF 360 데이터셋에서 렌더링 품질을 비교한 결과이다.
2. Ablation
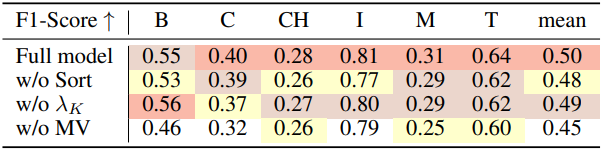
다음은 ablation study 결과이다. (TNT 데이터셋)

다음은 멀티뷰 정규화에 대한 ablation 결과이다. (TNT 데이터셋)
