[논문리뷰] Periodic Vibration Gaussian: Dynamic Urban Scene Reconstruction and Real-time Rendering
arXiv 2023. [Paper] [Page] [Github]
Yurui Chen, Chun Gu, Junzhe Jiang, Xiatian Zhu, Li Zhang
Fudan University | University of Surrey
30 Nov 2023

Introduction
거리, 도시 등 광범위한 도시 공간의 기하학적 재구성은 디지털 지도, 자동 내비게이션, 자율 주행과 같은 응용 분야에서 중추적인 역할을 해왔다. 현실 세계는 공간적, 시간적 차원 모두에서 본질적으로 동적이고 복잡하다. 주로 정적 장면에 초점을 맞춘 NeRF와 같은 장면 표현 기술의 발전에도 불구하고 더 까다로운 동적 요소를 간과한다.
동적 장면을 모델링하는 최근 접근 방식에는 NSG가 있으며 동적 장면을 장면 그래프로 분해하고 구조화된 표현을 학습한다. PNF는 panoptic segmentation을 통합하여 장면을 객체와 배경으로 더 분해한다. 그러나 정확한 객체 수준 감독을 얻는 것이 어려운 실제 시나리오에서는 확장성 문제가 발생하며 각 객체를 선형적으로 명시적으로 표현하면 객체 수에 따라 모델 복잡도가 증가한다.
SUDS는 나중에 정적 및 동적 요소와 장면의 환경 요인을 별도로 모델링하기 위해 3개 분기 아키텍처에서 객체 라벨링의 엄격한 요구 사항을 완화하기 위해 optical flow를 사용할 것을 제안하였다. NeRF 표현을 채택했음에도 불구하고 이러한 방법은 학습과 렌더링 모두에서 효율성이 낮아 대규모 장면 렌더링 및 재구성에 심각한 병목 현상을 초래한다. 또한 구성 부품을 수동으로 분리하면 설계가 복잡해지고 본질적인 상관 관계 및 상호 작용을 포착하는 능력이 제한된다.
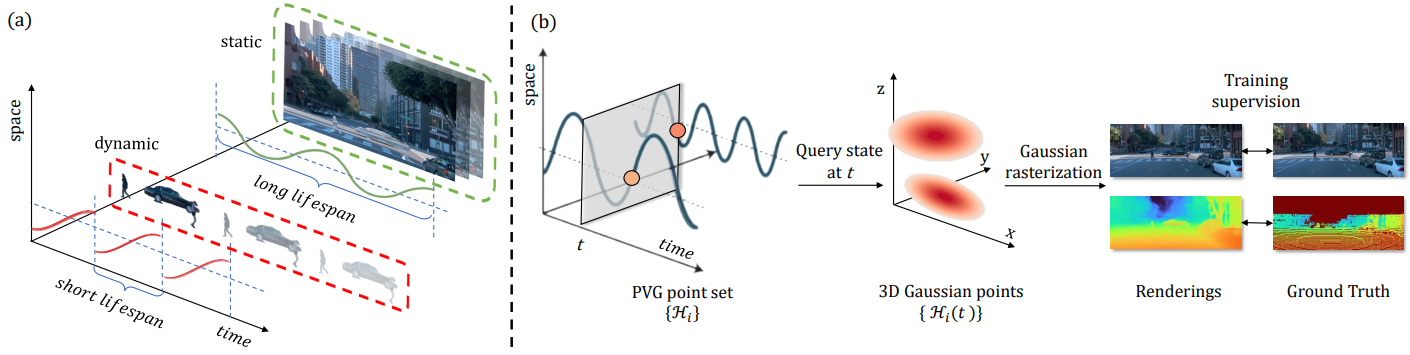
확인된 한계를 극복하기 위해 본 논문에서는 Periodic Vibration Gaussian (PVG)라는 새로운 동적 장면 표현 방법을 도입하였다. 이 접근 방식은 하나의 공식을 통해 장면 내 정적 요소와 동적 요소 모두의 통합 표현을 제공한다. 원래 정적 장면 표현을 위해 고안된 효율적인 3D Gaussian Splatting 기술을 기반으로 주기적 진동 기반 시간 역학을 통합한다. 이 수정을 통해 속도와 staticness와 같은 명시적인 모션 속성을 사용하여 정적 및 동적 장면 요소를 일관되게 표현할 수 있다. 또한 일반적으로 제한된 학습 데이터를 사용하여 표현 학습의 시간적 연속성을 향상시키기 위해 scene flow 기반 temporal smoothing 메커니즘과 position-aware point adaptive control 전략을 도입하였다.
Method
일련의 이미지 $\mathcal{I}$를 포괄하는 순차적으로 획득되고 보정된 멀티센서 데이터를 활용한다. 각각은 해당 intrinsic matrix $\mathbf{I}$와 extrinsic matrix $\mathbf{E}$가 장착된 카메라로 캡처되고 각각의 캡처 타임스탬프 $t$와 함께 \(\{\mathcal{I}_i, t_i, \mathbf{E}_i, \mathbf{I}_i \vert i = 1, 2, \ldots N_c\}\)로 저장된다. 또한 타임스탬프가 기록된 LiDAR 포인트 클라우드 \(\{(x_i, y_i, z_i, t_i) \vert i = 1, 2, \ldots N_l\}\)를 활용한다. 본 논문은 정확한 3D 재구성을 달성하고 원하는 타임스탬프 $t$와 카메라 포즈에서 새로운 뷰를 합성하는 것을 목표로 한다. 이를 위해 본 논문의 프레임워크는 렌더링 함수 \(\hat{\mathcal{I}} = \mathcal{F}_\theta (\mathbf{E}_o, \mathbf{I}_o, t)\)에 근접하도록 꼼꼼하게 설계되었다.
1. Preliminary
3D Gaussian Splatting 논문 리뷰 참조
2. Periodic Vibration Gaussian
Periodic Vibration Gaussian (PVG) 모델은 몇 가지 독특한 특징이 있다.
- Dynamics introduction: 시간이 지남에 따라 해당 포인트가 가장 두드러지는 순간을 나타내는 life peak($\tau$)의 개념을 도입한다. 이 개념의 동기는 각 Gaussian point에 고유한 수명을 할당하여 적극적으로 기여하는 시기와 어느 정도까지 정의하는 것이다. 이는 근본적으로 모델에 동적 특성을 주입하여 시간이 지남에 따라 장면 렌더링에 영향을 미치는 Gaussian point들의 변형을 가능하게 한다.
- Periodic vibration: 3D Gaussian의 평균 $\boldsymbol{\mu}$와 불투명도 $o$를 life peak $\tau$를 중심으로 하는 시간 종속 함수 \(\tilde{\boldsymbol{\mu}}(t)\)와 $\tilde{o}(t)$로 수정한다. 두 함수 모두 $\tau$에서 정점에 이른다. 이러한 적응을 통해 모델은 동적 동작을 효과적으로 캡처할 수 있으며 시간적 변화에 따라 각 Gaussian point를 조정할 수 있다.
모델 $\mathcal{H}$는 다음과 같이 표현된다.
\[\begin{aligned} \mathcal{H}(t) &= \{ \tilde{\boldsymbol{\mu}}(t), \mathbf{q}, \mathbf{s}, \tilde{o}(t), \mathbf{c} \} \\ \tilde{\boldsymbol{\mu}}(t) &= \boldsymbol{\mu} + \mathbf{A} \cdot \sin (\frac{2\pi (t - \tau)}{l}) \\ \tilde{o}(t) &= o \cdot e^{-\frac{1}{2} (t-\tau)^2 \beta^{-2}} \end{aligned}\]여기서 \(\tilde{\boldsymbol{\mu}}(t)\)는 life peak $\tau$에서 발생하는 $\boldsymbol{\mu}$를 중심으로 하는 진동하는 모션을 나타내고, $\tilde{o}(t)$는 진동하는 불투명도를 나타낸다. 특히, 파라미터 $\beta$는 $\tau$ 주변의 수명을 제어하며, 값이 클수록 수명이 더 크다는 것을 나타낸다. 파라미터 $l$은 장면 prior 역할을 하는 사이클 길이를 나타낸다. 파라미터 $\mathbf{A} \in \mathbb{R}^3$은 진동 방향을 나타낸다. 따라서 모델 $\mathcal{H}$의 학습 가능한 파라미터에는 \(\{\boldsymbol{\mu}, \mathbf{q}, \mathbf{s}, o, \mathbf{c}, \tau, \beta, \mathbf{A}\}\)가 포함된다.
특히 주기적인 진동을 통해 평균 벡터 \(\tilde{\boldsymbol{\mu}}(t)\)를 표현하여 정적 패턴과 동적 패턴 모두에 대한 응집력 있는 프레임워크를 제공한다. 명확성을 높이기 위해 PVG point가 나타내는 정적 정도를 정량화하고 포인트의 수명과도 연관되는 staticness coefficient $\rho = \frac{\beta}{l}$을 도입한다. 주기적인 진동은 $\rho$가 클 때 $\mu$ 부근의 수렴을 촉진한다. 이는 $\mathbf{A}$에 의한 \(\tilde{\boldsymbol{\mu}}(t)\)의 제한된 특성과 \(\mathbb{E}[\tilde{\boldsymbol{\mu}}(t)] = \boldsymbol{\mu}\)가 $\mathbf{A}$와 관계없이 $l$의 배수인 길이를 갖는 모든 시간 간격에 대해 유지된다는 사실에 기인한다.
3DGS는 $\mathbf{A} = 0$이고 $\rho = +\infty$인 PVG의 특정 케이스이다. $\rho$가 큰 PVG는 \(\| \mathbf{A} \|\)가 합리적인 범위 내에 유지되는 경우 장면의 정적 측면을 효과적으로 캡처한다.
장면의 동적 측면을 표현하는 PVG의 능력은 $\rho$가 작은 포인트에서 특히 두드러진다. $\rho \rightarrow 0$에 접근하는 포인트는 거의 순간적으로 나타나고 사라지며 시간 $\tau$ 주위에 선형 이동으로 나타난다. 시간이 지남에 따라 이러한 포인트들은 진동을 겪으며 일부는 사라지고 일부는 새로 나타난다. 특정 타임스탬프 $t$에서 동적 객체는 $\tau$가 $t$에 가까운 포인트로 주로 표현될 가능성이 더 높다. 본질적으로 여러 포인트가 고유한 타임스탬프에서 동적 개체를 나타내는 역할을 담당한다.
반대로, 장면의 정적 성분은 큰 $\rho$를 나타내는 포인트로 효과적으로 표현될 수 있다. $\rho$에 임계값을 도입하면 점이 동적 요소를 나타내는지 여부를 식별할 수 있다.
주어진 시간 $t$에서 모델은 $\mathcal{H}(t)$로 표시되는 특정 3D Gaussian 모델의 형태를 취한다. 동적인 장면을 효과적으로 표현하기 위해 $${\mathcal{H}(t)}$로 표시된 PVG point의 모음을 학습한다. 그런 다음 렌더링 프로세스가 다음과 같이 실행된다.
\[\begin{equation} \hat{\mathcal{I}} = \textrm{Render} (\{\mathcal{H}_i (t) \vert i = 1, \ldots, N_H\}; \mathbf{E}, \mathbf{I}) \end{equation}\]여기서 $N_H$는 장면의 PVG point 수를 나타낸다. 학습 파이프라인은 아래 그림과 같다.
3. Position-aware point adaptive control
3DGS에서 도입된 기존의 적응 제어(adaptive control) 방법은 각 Gaussian point를 균일하게 처리하므로 도시 장면에는 적합하지 않다. 이는 주로 제한되지 않은 장면의 중심에서 대부분의 포인트에 대한 평균 벡터 $\boldsymbol{\mu}$의 상당한 거리에 기인한다. 정확성을 유지하면서 더 적은 수의 포인트로 장면을 충실하게 표현하기 위해 먼 위치에는 더 큰 포인트를, 가까운 지역에는 더 작은 포인트를 활용하는 것이 좋다.
카메라 포즈가 중앙에 있다고 가정하면 각 PVG point에 대한 효과적인 제어를 위해서는 다음과 같이 정의된 scale factor $\gamma(\boldsymbol{\mu})$를 포함하는 것이 필수적이다.
\[\begin{equation} \gamma(\boldsymbol{\mu}) = \begin{cases} 1 & \; \textrm{if} \quad \| \boldsymbol{\mu} \|_2 < 2r \\ \| \boldsymbol{\mu} \|_2 / r - 1 & \; \textrm{if} \quad \| \boldsymbol{\mu} \|_2 \ge 2r \end{cases} \end{equation}\]여기서 $r$은 장면 반경(즉, 장면 범위)을 나타낸다. 특히, view space의 역방향 기울기가 지정된 threshold를 초과할 때 PVG $\mathcal{H}(t)$에 대한 densification 전략을 사용한다. $\max(\mathbf{s}) \le g \cdot \gamma(\boldsymbol{\mu})$인 경우 PVG를 복제(clone)하고, $g$는 scale에 대한 threshold 역할을 한다. 반대로, 이 조건이 충족되지 않으면 분할(split) 연산을 시작한다. 또한 주어진 PVG가 지나치게 큰지 여부를 식별하기 위해 $b$를 scale threshold로 사용하여 $\max(\mathbf{s}) > b \cdot \gamma (\boldsymbol{\mu})$인 점을 잘라내는 연산을 수행한다.
4. Model training
Temporal smoothing by scene flow
자율 주행에서 동적 장면을 재구성하는 것은 주로 뷰와 타임스탬프 측면에서 sparse한 데이터와 프레임 전반에 걸쳐 제한되지 않는 변형으로 인해 중요한 문제를 제기한다. 특히 PVG에서는 개별 포인트가 좁은 시간 window만 포함하므로 학습 데이터가 제한되고 overfitting에 대한 민감성이 높아진다. 이 문제를 해결하기 위해 연속되는 관측의 state 간의 연결을 설정하는 PVG의 고유한 동적 속성을 활용한다.
다음과 같이 scene velocity 메트릭을 도입한다.
\[\begin{equation} \mathbf{v} = \frac{d \tilde{\boldsymbol{\mu}}}{dt} \bigg\vert_{t = \tau} \cdot \exp (-\frac{\rho^2}{2}) = \frac{2 \pi \mathbf{A}}{l} \cdot \exp (-\frac{\rho^2}{2}) \end{equation}\]이 메트릭은 $\lim_{\rho \rightarrow \infty} \mathbf{v} = \mathbf{0}$과 $\lim_{\rho \rightarrow 0} \mathbf{v} = \frac{2 \pi \mathbf{A}}{l}$를 충족하므로 상한과 하한이 있다.
실제 시나리오에서 동적 개체는 짧은 시간 간격 내에 일정한 속도를 유지하는 경우가 많다. 이 관찰은 PVG의 연속되는 상태 사이에 선형 관계로 이어진다.
두 개의 인접한 타임스탬프 $t_1$과 $t_2$ $(t_1 < t_2)$를 고려하고 각각의 state는 \(\{\mathcal{H}_i (t_1)\}\)과 \(\{\mathcal{H}_i (t_2)\}\)로 표시된다. 이러한 state들은
\[\begin{equation} \Delta \boldsymbol{\mu} = \mathbf{v} \cdot (t_2 − t_1) = \mathbf{v} \cdot \Delta t \end{equation}\]로 표시되는 각 포인트에 대한 scene flow translation에 의해 선형적으로 연결된다. 구체적으로 $\mathcal{H}(t_2)$의 state를 다음과 같이 추정한다.
\[\begin{equation} \hat{\mathcal{H}} (t_2) = \{ \tilde{\boldsymbol{\mu}} (t_1) + \mathbf{v} \cdot \Delta t, \mathbf{q}, \mathbf{s}, \tilde{o} (t_1), \mathbf{c} \} \end{equation}\]이 추정 프로세스는 각 개별 PVG point에 적용된다. 이 추정의 시각적 표현은 아래 그림에 나와 있다.
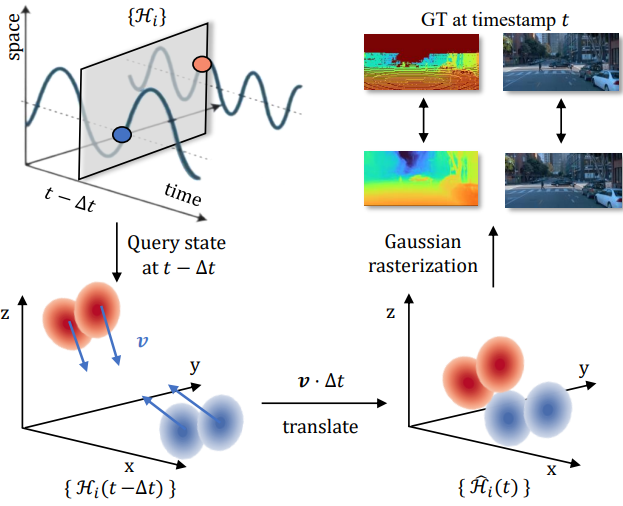
추정된 state를 활용하여 모델 학습을 개선한다. 구체적으로 $\Delta t$를 0으로 설정하기 위해 $\eta$의 확률을 할당하고 (추정값 없음을 나타냄) 나머지 확률에 대해 균일 분포 $\textrm{U}(−\delta, +\delta)$에서 $\Delta_t$를 무작위로 샘플링한다. 후자의 경우 학습 중에 $\mathcal{H}$를 $\hat{\mathcal{H}}$로 대체한다. 이러한 수정을 통해 모델은 기본 역학을 파악하여 계산 요구 사항을 크게 늘리지 않고도 보다 일관된 표현을 육성할 수 있다. 이 접근 방식을 채택함으로써 시간적 일치와 일관성을 향상시켜 sparse한 데이터로 인한 overfitting 문제와 위험을 완화한다.
Sky refinement
하늘의 고주파수 디테일을 처리하기 위해 고해상도 환경 큐브 맵 $f_\textrm{sky}(d) = c_\textrm{sky}$를 활용한다. 최종 색상은 $C_f = C + (1 − O) f_\textrm{sky}(d)$로 표현된다. 여기서 $O = \sum_{i=1}^{N_H} T_i \alpha_i$는 렌더링된 불투명도를 나타낸다. 학습 단계에서 안티 앨리어싱을 향상시키기 위해 단위 픽셀 길이 내에서 광선 방향 $d$에 무작위 섭동(perturbation)을 통합한다.
Objective
Loss function은 다음과 같다.
\[\begin{aligned} \mathcal{L} &= (1 - \lambda_r) \mathcal{L}_1 + \lambda_r \mathcal{L}_\textrm{ssim} + \lambda_d \mathcal{L}_d + \lambda_o \mathcal{L}_o + \lambda_v \mathcal{L}_v \\ \mathcal{L}_d &= \frac{1}{hw} \sum \| \mathcal{D}^s - \mathcal{D} \|_1 \\ \mathcal{L}_o &= − \frac{1}{hw} \sum O \cdot \log O − \frac{1}{hw} \sum M_\textrm{sky} \cdot \log (1 − O) \\ \mathcal{L}_v &= \frac{1}{hw} \sum \| \mathcal{V} \|_1 \end{aligned}\]여기서 \(\mathcal{L}_1\)과 \(\mathcal{L}_\textrm{ssim}\)은 RGB 렌더링 supervision을 위한 L1 loss와 SSIM loss이다.
\(\mathcal{L}_d\) 항은 기하학적 인식을 위한 depth loss이다. 여기서 $\mathcal{D}^s$는 LiDAR 포인트를 카메라 평면에 투영하여 생성된 sparse한 inverse depth map이고, $\mathcal{D}$는 렌더링된 깊이 맵의 inverse이다. $h$와 $w$는 렌더링 공간 크기이다.
\(\mathcal{L}_o\) 항은 opacity loss이며, $M_\textrm{sky}$는 사전 학습된 segmentation model에 의해 추정된 하늘 마스크이다. 이 loss는 불투명도 값을 0(투명한 하늘) 또는 1로 가이드하는 것을 목표로 한다. 특히 예측된 하늘 픽셀에 대해 불투명도를 0으로 정규화한다.
마지막 항 \(\mathcal{L}_v\)는 sparse velocity loss이며, $\mathcal{V}$는 렌더링된 속도 $v$의 맵이다. 이 loss는 sparse한 \(\| \mathbf{A} \|\)로 이어질 뿐만 아니라 장면의 대부분의 요소가 정적이기 때문에 더 큰 $\beta$를 장려한다.
Experiments
- 데이터셋: Waymo Open Dataset, KITTI
- 구현 디테일
- 포인트 초기화: LiDAR 포인트 $6 \times 10^5$개
- 가까운 점 $2 \times 10^5$개 (거리 $\sim \textrm{U}(0, r)$)
- 먼 점 $2 \times 10^5$개 (1/거리 $\sim \textrm{U}(0, 1/r)$)
- $r$: 전경 반경 (대략 30미터)
- $\beta$는 0.3으로, $\mathbf{A}$는 0으로 초기화
- optimizer: Adam
- 기존 3DGS의 설정을 따름
- $\mathbf{A}$, $\beta$, $o$의 learning rate는 각각 $3 \times 10^{-5}$, 0.02, 0.005으로 변경
- densification threshold: $1.7 \times 10^{-4}$
- 3,000 iteration마다 opcaity를 0.01로 리셋
- $\lambda_r = 0.2$, $\lambda_d = 0.1$, $\lambda_o = 0.05$, $\lambda_v = 0.01$
- $\Delta t = 1.5$, $\eta = 0.5$
- $l = 0.2$로 고정
- 큐브 맵 해상도: 1024
- GPU: NVIDIA RTX A6000 GPU
- iteration: 30,000
- 포인트 초기화: LiDAR 포인트 $6 \times 10^5$개
1. Comparison with state of the art
다음은 Waymo와 KITTI의 동적 장면에서의 이미지 재구성 및 novel view synthesis 결과를 정량적으로 비교한 표이다.

다음은 동적 재구성 결과를 비교한 것이다.

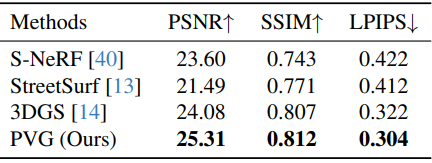
다음은 Waymo의 정적 장면에서의 novel view synthesis를 정량적으로 비교한 것이다.

다음은 Waymo의 정적 장면에서의 이미지 재구성 결과를 정량적으로 비교한 표이다.

다음은 렌더링된 RGB, 깊이, semantic label이다.

2. Ablation study
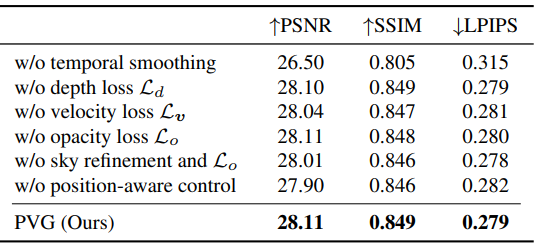
다음은 모델의 주요 구성 요소에 대한 ablation study 결과이다.
다음은 temporal smoothing 메커니즘에 대한 ablation study 결과이다.

다음은 사이클 길이 $l$에 대한 ablation study 결과이다.
