[논문리뷰] PUP 3D-GS: Principled Uncertainty Pruning for 3D Gaussian Splatting
CVPR 2025. [Paper] [Page] [Github]
Alex Hanson, Allen Tu, Vasu Singla, Mayuka Jayawardhana, Matthias Zwicker, Tom Goldstein
University of Maryland, College Park
14 Jun 2024

Introduction
최근 렌더링된 이미지에 미미한 영향을 미치는 Gaussian을 제거하기 위해, 3DGS 모델의 필요 저장 공간을 줄이는 여러 휴리스틱 기반 방법들이 제안되었다. 본 논문에서는 어떤 Gaussian을 제거할지 결정하기 위한 보다 수학적인 원칙에 기반한 접근 방식을 제안한다.
본 논문은 수렴된 장면에서 학습 이미지의 reconstruction error에 대한 Hessian으로부터 도출된 쉽게 계산할 수 있는 민감도 점수를 도입하였으며, 민감도 점수를 사용하여 Gaussian을 제거한 다음 나머지 Gaussian을 fine-tuning하였다. 이를 통해 이미지 품질을 유지하면서 Gaussian의 80%를 제거할 수 있다.
또한, 이 접근 방식은 두 번째 pruning 및 fine-tuning을 가능하게 한다. 이 multi-round pruning 방식은 Gaussian의 90%를 제거하는 동시에 기존의 휴리스틱 기반 방법보다 렌더링 속도와 이미지 품질 면에서 월등한 성능을 보인다. 또한 3DGS의 학습 프레임워크를 수정하거나 quantization 기반 기법을 적용하여 저장 공간을 줄이는 여러 다른 방법들과 동시에 사용하여 성능을 더욱 향상시키고 모델을 압축할 수 있다.
Method
1. Fisher Information Matrix
장면을 포즈를 아는 이미지의 집합 \((\mathcal{P}_\textrm{gt}, \mathcal{I}_\textrm{gt})\)로 재구성하려면 각 시점의 2D 이미지 평면에 projection해야 한다. 이는 장면을 재구성하는 Gaussian의 위치와 크기에 불확실성을 야기한다. 카메라에서 멀리 떨어진 큰 Gaussian은 카메라 가까이 있는 작은 Gaussian으로 픽셀 공간에서 동등하게 모델링될 수 있다. 즉, 충분한 수의 카메라에서 인식되지 않는 Gaussian이라도 다양한 위치와 스케일에서 입력 시점의 이미지를 재구성할 수 있다.
저자들은 3DGS의 불확실성을 Gaussian의 위치와 스케일과 같은 파라미터가 입력 뷰에 대한 reconstruction loss에 영향을 미치지 않고 얼마나 교란될 수 있는지로 정의하였다. 구체적으로, 이는 특정 Gaussian에 대한 입력 뷰에 대한 오차의 민감도이다. Gaussian 집합 $\mathcal{G}$를 입력으로 받고 학습 뷰 집합에 대한 오차 값을 출력하는 loss function \(L : \mathbb{R}^\mathcal{G} \rightarrow \mathbb{R}\)이 주어지면, 이 민감도는 Hessian \(\nabla_\mathcal{G}^2 L\)로 표현될 수 있다.
Gaussian별 민감도를 얻으려면 먼저 재구성 이미지 \(I_\mathcal{G}\)에 대한 $L_2$ error를 구해야 한다.
\[\begin{equation} L_2 = \frac{1}{2} \sum_{\phi \in \mathcal{P}_\textrm{gt}} \| I_\mathcal{G} (\phi) - I_\textrm{gt} \|_2^2 \end{equation}\]이것을 두 번 미분하면 Hessian이 된다.
\[\begin{equation} \nabla_\mathcal{G}^2 L_2 = \sum_{\phi \in \mathcal{P}_\textrm{gt}} \nabla_\mathcal{G} I_\mathcal{G} (\phi) \nabla_\mathcal{G} I_\mathcal{G} (\phi)^\top + (I_\mathcal{G} (\phi) - I_\textrm{gt}) \nabla_\mathcal{G}^2 I_\mathcal{G} (\phi) \end{equation}\]수렴된 3DGS 모델에서 \(\| I_\mathcal{G} (\phi) - I_\textrm{gt} \|_1\)은 0에 가까워져 2차 항이 사라진다.
\[\begin{equation} \nabla_\mathcal{G}^2 L_2 = \sum_{\phi \in \mathcal{P}_\textrm{gt}} \nabla_\mathcal{G} I_\mathcal{G} (\phi) \nabla_\mathcal{G} I_\mathcal{G} (\phi)^\top \end{equation}\]이는 Fisher Information matrix이다. \(\nabla_\mathcal{G} I_\mathcal{G}\)는 재구성된 이미지에 대한 gradient이므로, 이 근사값은 입력 포즈 \(\mathcal{P}_\textrm{gt}\)에만 의존하며 입력 이미지 \(I_\textrm{gt}\)에는 의존하지 않는다.
2. Sensitivity Pruning Score
모델 파라미터에 대한 전체 Hessian은 \(\nabla_\mathcal{G}^2 L \in \mathbb{R}^{\mathcal{G} \times \mathcal{G}}\)은 각 Gaussian의 파라미터 수의 제곱에 비례한다. 그러나 파라미터의 일부만 사용하여도 효과적인 민감도 점수를 얻는 데 충분하다.
각 Gaussian \(\mathcal{G}_i\)에 대한 민감도 점수를 얻기 위해, Gaussian 간 파라미터 관계만 포착하는 Hessian의 block diagonal으로 범위를 제한한다. 이를 통해 각 block을 Gaussian별 Hessian으로 사용하여 독립적인 민감도 점수를 얻을 수 있다.
\[\begin{equation} \textbf{H}_i = \nabla_{\mathcal{G}_i} I_{\mathcal{G}} \nabla_{\mathcal{G}_i} I_{\mathcal{G}}^\top \end{equation}\]직관적으로, 각 block Hessian \(\textbf{H}_i\)는 \(\mathcal{G}_i\)의 매개변수만 교란했을 때 reconstruction error에 미치는 영향을 개별적으로 측정한다. \(\textbf{H}_i\)를 민감도 점수 \(\tilde{U}_i \in \mathbb{R}\)로 변환하기 위해 log determinant를 사용한다.
\[\begin{equation} \tilde{U}_i = \log \vert \textbf{H}_i \vert = \log \vert \nabla_{\mathcal{G}_i} I_{\mathcal{G}} \nabla_{\mathcal{G}_i} I_{\mathcal{G}}^\top \vert \end{equation}\]이는 Gaussian \(\mathcal{G}_i\)의 모든 파라미터가 reconstruction error에 미치는 상대적인 영향을 포착한다.
저자들은 Gaussian 파라미터들 중 위치 $x_i$와 scaling $s_i$만 고려하여 효과적인 민감도 점수를 얻을 수 있음을 발견했다. 최종 민감도 가지치기 점수 $U_i \in \mathbb{R}$은 다음과 같다.
\[\begin{equation} U_i = \log \vert \textbf{H}_i \vert = \log \vert \nabla_{x_i, s_i} I_{\mathcal{G}} \nabla_{x_i, s_i} I_{\mathcal{G}}^\top \vert \end{equation}\]3. Patch-wise Uncertainty
전체 장면에 대한 Hessian을 계산하려면 재구성된 입력 뷰의 모든 픽셀별 Fisher 근사값에 대한 합이 필요하다. 그러나 이미지 패치에 대해 계산된 민감도 점수는 개별 픽셀에 대해 계산된 점수와 높은 상관관계를 갖는다.
구체적으로, 이미지를 저해상도로 렌더링한 후 각 픽셀에 대해 Fisher 근사값을 계산하여 이미지 패치에 대한 Fisher 근사값을 계산한다. 그런 다음, 모든 뷰에 대한 패치별 Fisher 근사값을 합하여 장면 수준의 Hessian을 얻는다. (4$\times$4 이미지 패치를 사용)
4. Multi-Round Pipeline
모델을 pruning한 후 추가적인 densification 없이 fine-tuning한다. 이 과정을 prune-refine라고 부른다. 많은 경우, 모델은 fine-tuning 후 \(\|I_\mathcal{G} - I_\textrm{gt}\|_1\)가 다시 작아진다. 이를 통해 여러 라운드에 걸쳐 prune-refine을 반복할 수 있다. 경험적으로 여러 라운드의 prune-refine이 동일한 단일 라운드의 prune-refine보다 성능이 우수했다고 한다.
Experiments
1. Results
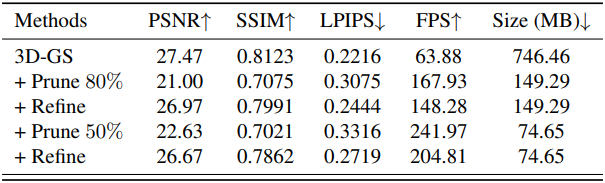
다음은 각 prune refine 단계에 따른 이미지 품질, FPS, 저장 공간을 비교한 표이다.
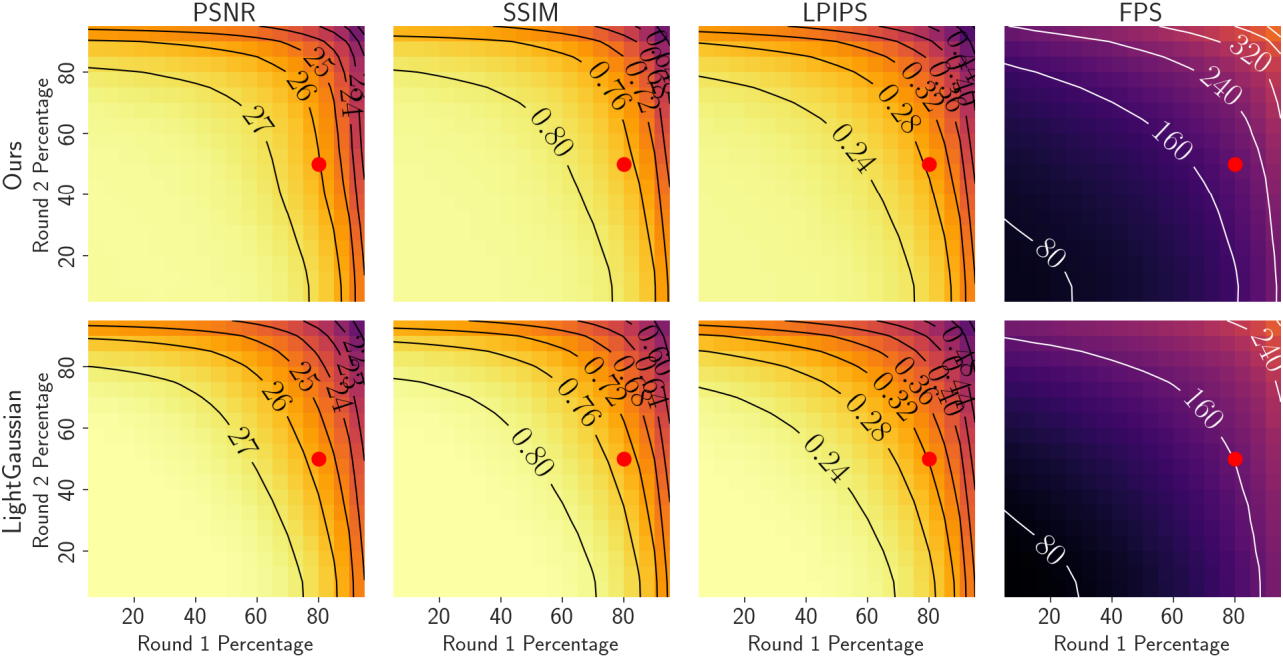
다음은 각 라운드의 pruning 비율에 따른 이미지 품질과 FPS를 LightGaussian과 비교한 결과이다. (빨간 점은 (80%, 50%)로 90% 압축)
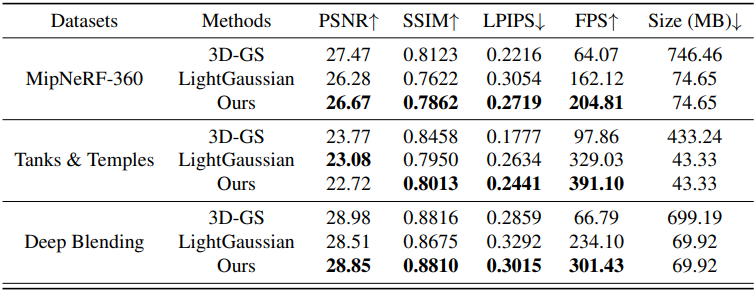
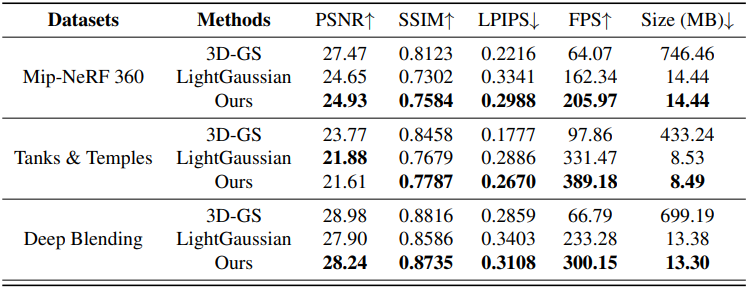
다음은 3DGS 및 LightGaussian과의 비교 결과이다.

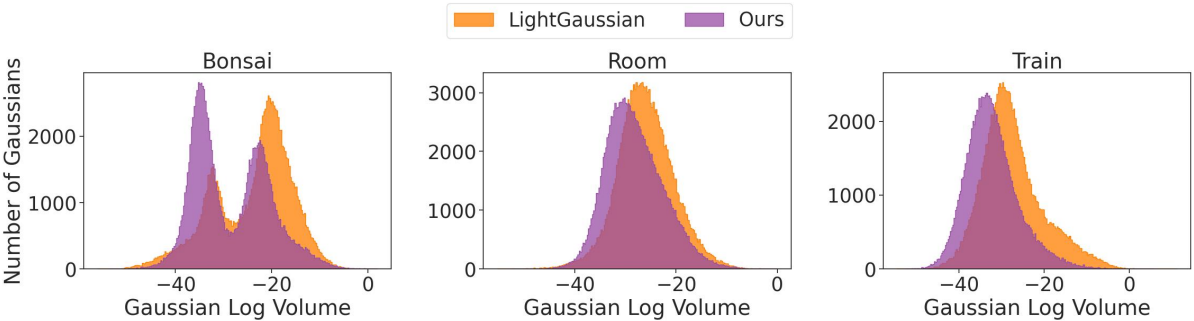
다음은 두 번의 prune-refine 후의 Gaussian들의 분포를 LightGaussian과 비교한 그래프이다. PUP 3D-GS는 작은 Gaussian들이 더 많이 살아 남기 때문에 LightGaussian보다 렌더링 속도와 이미지 품질이 더 좋다.
다음은 Vectree Quantization를 적용한 후의 결과를 비교한 표이다.
2. Ablations
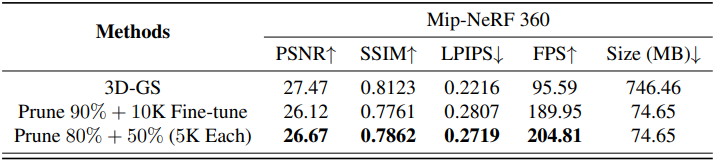
다음은 두 번의 prune-refine과 한 번의 prune-refine을 비교한 결과이다. (동일한 압축률과 iteration 수)
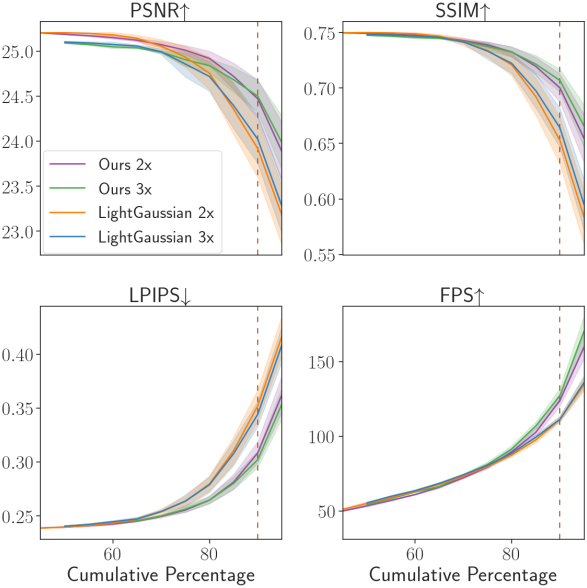
다음은 두 번의 prune-refine과 세 번의 prune-refine을 누적 압축률에 따라 비교한 결과이다.
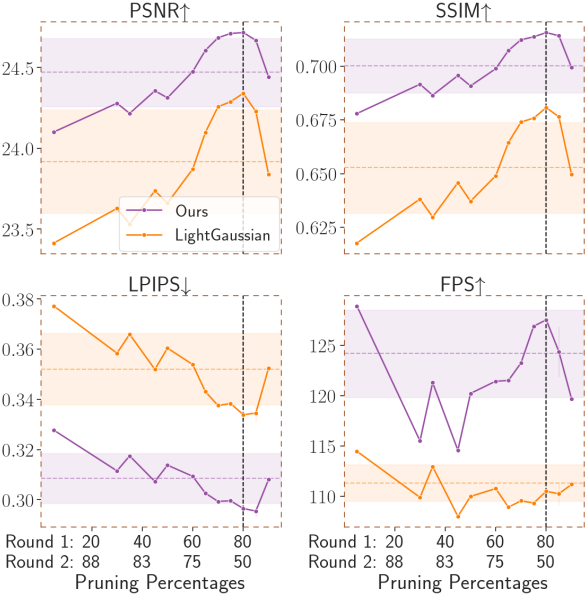
다음은 각 prune-refine 단계의 pruning 비율에 대한 비교 결과이다. (모두 압축률 90%)
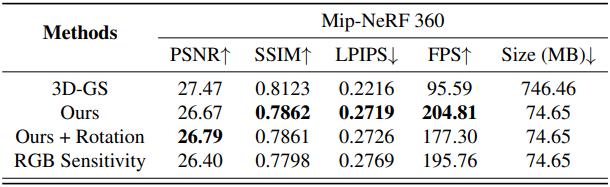
다음은 민감도 계산에 사용한 파라미터에 대한 ablation 결과이다.
Limitations
- L1 residual이 충분히 작아야 Fisher 근사가 정확해진다.
- Fisher matrix 계산에 많은 메모리가 필요하다.