[논문리뷰] ProlificDreamer: High-Fidelity and Diverse Text-to-3D Generation with Variational Score Distillation

NeurIPS 2023 (Spotlight). [Paper] [Page]
Zhengyi Wang, Cheng Lu, Yikai Wang, Fan Bao, Chongxuan Li, Hang Su, Jun Zhu
Tsinghua University | Renmin University of China | ShengShu
25 May 2023

Introduction

Diffusion model은 특히 대규모 데이터셋에 대해 학습할 때 text-to-image 합성을 크게 향상시켰다. 이러한 발전에 영감을 받아 DreamFusion은 텍스트에서 3D 콘텐츠를 생성하기 위해 사전 학습된 대규모 text-to-image diffusion model을 사용하여 3D 데이터의 필요성을 피하였다. DreamFusion은 Score Distillation Sampling (SDS) 알고리즘을 도입하여 하나의 3D 표현을 최적화하여 모든 뷰에서 렌더링된 이미지가 높은 likelihood를 유지하도록 한다. 경험적 관찰에 따르면 SDS는 아직 완전히 설명되거나 적절하게 해결되지 않은 over-saturation, over-smoothing, 낮은 다양성 문제를 겪는 경우가 많다. 또한 렌더링 해상도나 distillation time schedule과 같은 text-to-3D를 위한 디자인 공간의 직교 요소가 완전히 탐색되지 않았으며 이는 추가 개선의 상당한 잠재력을 시사한다. 본 논문에서는 정교한 3D 표현을 얻기 위해 이러한 모든 요소에 대한 체계적인 연구를 제시하였다.

본 논문은 Variational Score Distillation (VSD)를 제시하였다. 이는 SDS에서와 같이 하나의 포인트 대신 텍스트 프롬프트가 제공된 해당 3D 장면을 확률 변수로 처리한다. VSD는 모든 뷰에서 렌더링된 이미지에 유도된 분포가 사전 학습된 2D diffusion model에 의해 정의된 분포와 최대한 가깝게 정렬되도록 KL divergnece 측면에서 3D 장면의 분포를 최적화한다. VSD는 여러 3D 장면이 잠재적으로 하나의 프롬프트에 정렬될 수 있는 현상을 자연스럽게 특성화한다. 이를 효율적으로 해결하기 위해 VSD는 입자 기반 variational inference를 채택하고 3D 분포를 나타내는 입자로 3D 파라미터 집합을 유지한다. 저자들은 Wasserstein gradient flow를 통해 입자에 대한 새로운 기울기 기반 업데이트 규칙을 도출하고 최적화가 수렴될 때 입자가 원하는 분포의 샘플이 될 것임을 보장한다. 이 업데이트에서는 사전 학습된 diffusion model의 Low-Rank Adaptation (LoRA)를 통해 효율적이고 구현될 수 있는 렌더링 이미지에 대한 분포의 score function을 추정해야 한다. 최종 알고리즘은 입자와 score function을 교대로 업데이트한다.

저자들은 단일 포인트 Dirac 분포를 variational distribution으로 사용하여 SDS가 VSD의 특별 케이스임을 보였다. 이 통찰력은 SDS에서 생성된 3D 장면의 제한된 다양성과 충실도를 설명한다. 또한 단일 입자를 사용하더라도 VSD는 parametric score model을 학습할 수 있어 잠재적으로 SDS보다 뛰어난 일반화를 제공한다. 또한 저자들은 다른 3D 요소를 분리하는 identity rendering function을 사용하여 2D 공간에서 SDS와 VSD를 실증적으로 비교하였다. Diffusion model의 ancestral sampling과 유사하게 VSD는 일반 CFG 가중치(ex. 7.5)를 사용하여 현실적인 샘플을 생성할 수 있다. 대조적으로, SDS는 over-saturation과 over-smoothing과 같은 text-to-3D에서 이전에 관찰된 것과 동일한 문제를 공유하여 좋지 못한 결과를 나타낸다.

저자들은 text-to-3D를 위한 알고리즘과 직교하는 다른 요소들을 체계적으로 연구하고 명확한 디자인 공간을 제시하였다. 구체적으로, 학습 중 512$\times512의 높은 렌더링 해상도와 시각적 품질 개선을 위한 어닐링된 distilling time schedule을 제안하였다. 또한 복잡한 장면 생성에 중요한 장면 초기화를 제안하였다. 본 논문의 접근 방식은 충실도가 높고 다양한 3D 결과를 생성할 수 있다. 저자들은 이 모델을 ProlificDreamer라고 부른다.

Variational Score Distillation

1. Sampling from 3D Distribution as Variational Inference

원칙적으로 텍스트 프롬프트 $y$가 주어지면 가능한 모든 3D 표현의 확률적 분포가 존재한다. $\theta$로 parameterize된 3D 표현(ex. NeRF)에서 이러한 분포는 확률적 밀도 $\mu (\theta \vert y)$로 모델링될 수 있다. $q_0^\mu (x_0 \vert c, y)$를 주어진 카메라 $c$와 렌더링 함수 $g(\cdot, c)$에 의해 렌더링된 이미지 $x_0 := g(\theta, c)$의 분포라 하자. 또한

\[\begin{equation} q_0^\mu (x_0 \vert y) := \int q_0^\mu (x_0 \vert c, y)p(c)dc \end{equation}\]

를 카메라 분포 $p(c)$에 대한 주변 분포라 하고, $p_0 (x_0 \vert y)$를 사전 학습된 text-to-image diffusion model에 의해 정의된 $t = 0$의 주변 분포라 하자. 높은 시각적 품질의 3D 표현을 얻기 위해 다음 문제를 풀어 분포 $\mu$의 샘플이 사전 학습된 diffusion model과 정렬하도록 최적화한다.

\[\begin{equation} \min_\mu D_\textrm{KL} (q_0^\mu (x_0 \vert y) \;\|\; p_0 (x_0 \vert y)) \end{equation}\]

이는 타겟 분포 $p_0 (x_0 \vert y)$를 근사화하기 위해 variational distribution $q_0^\mu (x_0 \vert y)$를 사용하는 일반적인 variational inference 문제이다.

$p_0$는 다소 복잡하고 $p_0$의 고밀도 영역은 고차원에서 극도로 희박할 수 있기 때문에 위 문제를 직접 해결하는 것은 어렵다. Diffusion model의 성공에 영감을 받아 저자들은 $t$로 인덱싱된 다양한 diffusion 분포를 사용하여 일련의 최적화 문제를 구성하였다. $t$가 $T$로 증가하면 diffusion 분포가 표준 가우시안 분포에 가까워지기 때문에 최적화 문제가 더 쉬워진다. VSD라고 하는 이러한 문제의 앙상블을 다음과 같이 동시에 해결한다.

\[\begin{aligned} \mu^\ast &:= \underset{\mu}{\arg \min} \mathbb{E}_t [(\sigma_t / \alpha_t) \omega (t) D_\textrm{KL} (q_t^\mu (x_t \vert y) \;\|\; p_t (x_t \vert y))] \\ &= \underset{\mu}{\arg \min} \mathbb{E}_{t,c} [(\sigma_t / \alpha_t) \omega (t) D_\textrm{KL} (q_t^\mu (x_t \vert c, y) \;\|\; p_t (x_t \vert y))] \end{aligned}\]

여기서

\[\begin{aligned} q_t^\mu (x_t \vert c, y) &:= \int q_0^\mu (x_0 \vert c, y) p_{t0} (x_t \vert x_0) dx_0 \\ q_t^\mu (x_t \vert y) &:= \int q_0^\mu (x_0 \vert y) p_{t0} (x_t \vert x_0) dx_0 \\ p_t (x_t \vert y) &= \int p_0 (x_0 \vert y) p_{t0} (x_t \vert x_0) dx_0 \\ p_{t0} &= \mathcal{N} (x_t \vert \alpha_t x_0, \sigma_t^2 I) \end{aligned}\]

이고, $\omega (t)$는 시간에 의존하는 가중치 함수이다.

하나의 포인트 $\theta$를 최적화하는 SDS와 비교하여 VSD는 $\theta$를 샘플링하는 전체 분포 $\mu$를 최적화한다. 특히, VSD에서 $t > 0$에 대한 추가 KL-divergence를 도입하는 것이 원래 문제의 글로벌 최적에 영향을 미치지 않는다.

\[\begin{equation} D_\textrm{KL} (q_t^\mu (x_t \vert y) \;\|\; p_t (x_t \vert y)) = 0 \Leftrightarrow q_0^\mu (x_0 \vert y) = p_0 (x_0 \vert y) \end{equation}\]

2. Update Rule for Variational Score Distillation

VSD를 해결하기 위한 직접적인 방법은 $\mu$에 대해 또 다른 parameterize된 생성 모델을 학습시키는 것일 수 있지만 이는 많은 계산 비용과 최적화 복잡도를 가져올 수 있다. 이전 입자 기반 variational inference 방법에서 영감을 받아 $n$개의 3D 파라미터 \(\{\theta\}_{i=1}^n\)을 입자로 유지하고 이에 대한 새로운 업데이트 규칙을 도출한다. 직관적으로, 현재 분포 $\mu$를 나타내기 위해 \(\{\theta\}_{i=1}^n\)을 사용하고, 최적화가 수렴한다면 $\theta^{(i)}$는 최적 분포 $\mu^\ast$의 샘플이 될 것이다. 이러한 최적화는 다음 정리와 같이 $\theta$에 대한 ODE를 시뮬레이션하여 실현할 수 있다.

---

Theorem: Wasserstein gradient flow of VSD

초기 분포 $\mu_0$부터 시작하여 각 시간 $\tau \ge 0$에서 분포 공간의 VSD 문제를 최소화하는 Wasserstein gradient flow $\mu$를 $\mu_\infty = \mu^\ast$인 \(\{\mu_t\}_{\tau \ge 0}\)이라 하자. 그러면 먼저 $\theta_0 \sim \mu_0(\theta_0 \vert y)$를 샘플링하고 다음과 같은 ODE를 시뮬레이션하여 $\mu_\tau$에서 $\theta_\tau$를 샘플링할 수 있다.

\[\begin{equation} \frac{d \theta_\tau}{d \tau} = - \mathbb{E}_{t, \epsilon, c} \bigg[ \omega (t) \bigg( \underbrace{-\sigma_t \nabla_{x_t} \log p_t (x_t \vert y)}_{\textrm{score of noisy real images}} - \underbrace{(-\sigma_t \nabla_{x_t} \log q_t^{\mu_t} (x_t \vert c, y))}_{\textrm{score of noisy rendered images}} \bigg) \frac{\partial g (\theta_\tau, c)}{\partial \theta_\tau} \bigg] \end{equation}\]

여기서 $q_t^{\mu_\tau}$는 ODE 시간 $\tau$에서의 $\mu_\tau$에 대한 시간 $t$에서의 noisy한 분포이다.

---

위 정리에 따르면 ODE를 시뮬레이션할 수 있다. 원하는 분포 $\mu^\ast$로부터 대략적으로 샘플링할 수 있을 만큼 충분히 큰 $\tau$에 대해. ODE는 각 시간 $\tau$에서 잡음이 있는 실제 이미지와 잡음이 있는 렌더링된 이미지의 score function을 포함한다. 잡음이 있는 실제 이미지의 score function $-\sigma_t \nabla_{x_t} \log p_t (x_t \vert y)$는 사전 학습된 diffusion model \(\epsilon_{\textrm{pretrain}} (x_t, t, y)\)로 근사될 수 있다. 잡음이 있는 렌더링된 이미지의 score function $-\sigma_t \nabla_{x_t} \log q_t^{\mu_t} (x_t \vert c, y)$는 또다른 noise 예측 네트워크 $\epsilon_\phi (x_t, t, c, y)$에 의해 추정된다. 여기서 $\epsilon_\phi$는 다음과 같이 표준 diffusion 목적 함수로 \(\{\theta^{(i)}\}_{i=1}^n\)에 의해 렌더링된 이미지에 대해 학습된다.

\[\begin{equation} \min_\phi \sum_{i=1}^n \mathbb{E}_{t \sim \mathcal{U} (0, 1), \epsilon \sim \mathcal{N} (0,I), c \sim p(c)} [\| \epsilon_\phi (\alpha_t g (\theta^{(i)}, c) + \sigma_t \epsilon, t, c, y) - \epsilon \|_2^2] \end{equation}\]

실제로 사전 학습된 모델 $\epsilon_\textrm{pretrain} (x_t, t, y)$의 작은 U-Net 또는 LoRA로 $\epsilon_\phi$를 parameterize하고 추가 카메라 파라미터 $c$를 네트워크의 조건 임베딩에 더한다. 대부분의 경우 LoRA를 사용하면 얻은 샘플의 충실도가 크게 향상될 수 있으며, 이는 LoRA가 효율적인 few-shot fine-Tuning을 위해 설계되었으며 $\epsilon_\textrm{pretrain}$의 사전 정보를 활용할 수 있기 때문이다.

각 ODE 시간 $\tau$에서 $\epsilon_\phi$가 현재 분포 $q_t^{\mu_\tau}$와 일치하는지 확인해야 한다. 따라서 $\epsilon_\phi$와 $\theta^{(i)}$를 교대로 최적화하고 각 입자 $\theta^{(i)}$는

\[\begin{equation} \theta^{(i)} \leftarrow \theta^{(i)} - \eta \nabla_\theta \mathcal{L}_\textrm{VSD} (\theta^{(i)}) \end{equation}\]

로 업데이트된다. 여기서 $\eta > 0$는 step size (learning rate)이다. 위의 Theorem에 따르면 해당 기울기는 다음과 같다.

\[\begin{equation} \nabla_\theta \mathcal{L}_\textrm{VSD} (\theta) = \mathbb{E}_{t, \epsilon, c} \bigg[ \omega(t) (\epsilon_\textrm{pretrain} (x_t, t, y) - \epsilon_\phi (x_t, t, c, y)) \frac{\partial g(\theta, c)}{\partial \theta} \bigg] \\ \textrm{where} \quad x_t = \alpha_t g(\theta, c) + \sigma_t \epsilon \end{equation}\]

3. Comparison with SDS

SDS는 VSD의 특수한 경우이다.

이론적으로 SDS와 VDS의 업데이트 규칙을 비교하면 SDS는 단일 포인트 Dirac 분포 $\mu (\theta \vert y) \approx \delta (\theta - \theta^{(1)})$을 variational distribution으로 사용하는 VSD의 특수한 경우이다. 특히, VSD는 잠재적으로 여러 입자를 사용할 뿐만 아니라 단일 입자($n = 1$)에 대해서도 parametric score function $\epsilon_\phi$를 학습하여 잠재적으로 SDS보다 우수한 일반화를 제공한다. 또한 VSD는 LoRA를 사용하여 $\epsilon_\phi (x_t, t, c, y)$에서 텍스트 프롬프트 $y$를 추가로 활용할 수 있는 반면 SDS에 사용되는 Gaussian noise $\epsilon$은 $y$의 정보를 활용할 수 없다.

VSD는 CFG에 친화적이다.

VSD는 사전 학습된 모델 $\epsilon_\textrm{pretrain}$에 의해 정의된 최적의 $\mu^\ast$에서 $\theta$를 샘플링하는 것을 목표로 하기 때문에 3D 샘플 $\theta$에 대해 $\epsilon_\textrm{pretrain}$에서 CFG를 조정함으로써 얻는 효과는 2D 샘플에 대한 효과와 매우 유사하다. 따라서 VSD는 기존의 text-to-image 방법만큼 유연하게 CFG를 튜닝할 수 있으며 최상의 성능을 위해 일반적인 text-to-image 생성 task와 동일한 CFG(ex. 7.5)를 사용한다. 이를 통해 VSD는 일반적으로 큰 CFG(ex. 100)가 필요했던 이전 SDS의 문제를 처음으로 해결하였다.

3D 표현을 분리하는 2D 실험의 VSD와 SDS

SDS와 VSD를 직접 비교하기 위해 최적화 알고리즘을 3D 표현에서 분리하는 렌더링 함수 $g(\theta)$의 특수한 경우를 고려하자. 특히, 임의의 $c$에 대해 $g(\theta, c) = \theta$로 설정한다. 그러면 렌더링된 이미지 $x = g(\theta, c) = \theta$는 $\theta$와 동일한 2D 이미지이다. 이러한 경우 파라미터 $\theta$를 최적화하는 것은 2D 공간에서 이미지를 생성하는 것과 동일하므로 3D 표현과 무관하다.

위 그림에는 다양한 샘플링 방법의 결과가 나와 있다. SDS는 작은 CFG 가중치와 큰 CFG 가중치 모두에서 실패한다. 특히 SDS에 사용되는 기본 CFG 가중치인 100을 사용하면 2D 샘플은 이전에 text-to-3D에서 관찰된 over-saturation 및 over-smoothing과 같은 동일한 문제를 공유한다. 이와 대조적으로 VSD는 다양한 CFG 가중치를 수용하는 유연성을 보여주고 일반 CFG 가중치(ex. 7.5)를 사용하여 현실적인 샘플을 생성하며 diffusion model과 유사하게 동작한다.

이 비교에서는 다른 3D 요소가 격리되므로 이러한 결과는 SDS의 문제가 지나치게 단순화된 variational distillation과 SDS에서 사용하는 대규모 CFG에서 비롯된다는 것을 시사한다. 이러한 결과는 text-to-3D 생성에 VSD를 사용하도록 강력하게 동기를 부여하며 여전히 SDS보다 실질적이고 지속적으로 성능이 뛰어나다.

ProlificDreamer

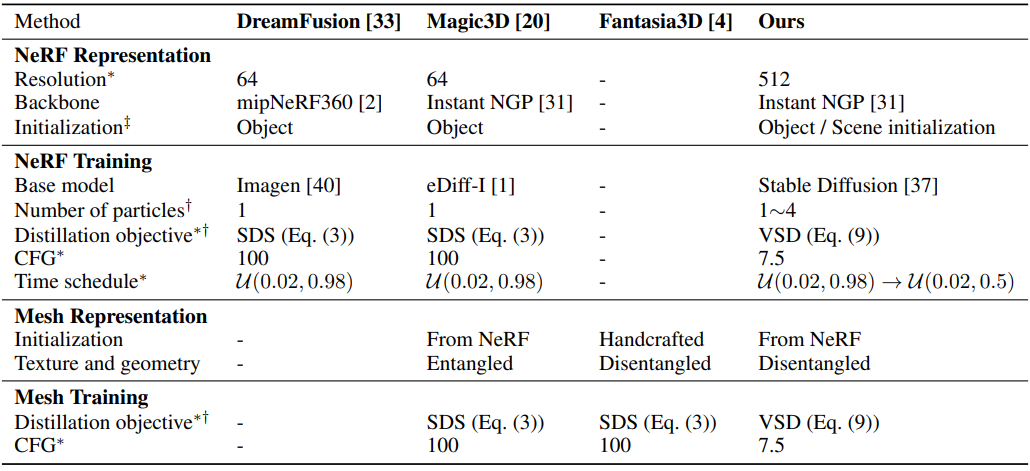
저자들은 text-to-3D를 위한 명확한 디자인 공간을 제시하고 distillation 알고리즘에 직교하는 다른 요소들을 체계적으로 연구하였다. 위 표에 강조된 모든 개선 사항을 결합하여 고급 text-to-3D 접근 방식인 ProlificDreamer에 도달했다.

1. Design Space of Text-to-3D Generation

본 논문은 text-to-3D 생성의 디자인 공간에서 몇 가지 개선 사항을 포함하는 2단계 접근 방식을 채택하였다. 특히 첫 번째 단계에서는 VSD를 통해 고해상도(ex. 512) NeRF를 최적화하여 복잡한 형상이 있는 장면을 생성하기 위해 높은 유연성을 활용한다. 두 번째 단계에서는 DMTet을 사용하여 첫 번째 단계에서 얻은 NeRF에서 텍스처 mesh를 추출하고 고해상도 디테일을 위해 텍스처 mesh를 추가로 fine-tuning한다. 두 번째 단계는 선택 사항이며, 이는 NeRF와 mesh는 모두 3D 콘텐츠를 표현하는 데 고유한 장점이 있고 특정 경우에 선호되기 때문이다. 그럼에도 불구하고 ProlificDreamer는 충실도가 높은 NeRF와 mesh를 모두 생성할 수 있다.

2. 3D Representation and Training

저자들은 알고리즘 공식과 직교하는 다른 요소를 체계적으로 연구하였다. 구체적으로 학습 시 512$\times$512의 높은 렌더링 해상도와 시각적 품질 향상을 위한 annealed distilling time schedule을 제안하였다. 또한 복잡한 장면 생성에 중요한 장면 초기화를 신중하게 디자인하였다.

NeRF 학습을 위한 고해상도 렌더링

효율적인 고해상도 렌더링을 위해 Instant NGP를 선택하고 VSD를 사용하여 최대 512 해상도로 NeRF를 최적화한다. SDS는 NeRF 최적화에서 주요 병목 현상 중 하나이다. 대신, VSD를 적용하면 64에서 512까지 다양한 해상도를 갖는 충실도가 높은 NeRF를 얻을 수 있다.

NeRF 학습을 위한 장면 초기화

NeRF의 밀도를

\[\begin{equation} \sigma_\textrm{init} (\mu) = \lambda_\sigma (1 − \frac{\| \mu \|_2}{r}) \end{equation}\]

로 초기화한다. 여기서 $\lambda_\sigma$는 밀도 강도, $r$은 밀도 반경, $\mu$는 좌표이다. 객체 중심 장면의 경우 Magic3D에서 사용되는 객체 중심 초기화를 따라 $\lambda_\sigma = 10$과 $r = 0.5$를 사용한다. 복잡한 장면의 경우 밀도를 비어 있게 만들기 위해 $\lambda_\sigma = -10$이고 카메라를 둘러싸는 $r = 2.5$로 장면 초기화을 제안하였다. 또한 \(\| \mu \|_2 < 5/6\)에 대해서는 객체 중심 초기화를 사용하고 다른 경우에는 장면 초기화를 사용하여 복잡한 장면에 중심 객체를 추가할 수 있다. 여기서 hyperparameter $5/6$은 초기 밀도 함수의 연속을 보장한다.

Score distillation을 위한 annealed time schedule

Score distillation 목적 함수에서 SDS와 VSD 모두에 적합한 간단한 2단계 어닐링을 활용한다. 처음 몇 step에서는 timestep $t \sim \mathcal{U}(0.02, 0.98)$를 샘플링한 다음 $t \sim \mathcal{U}(0.02, 0.50)$로 어닐링한다. 더 큰 $t$에 대한 KL-divergence는 학습 초기 단계에서 합리적인 최적화 방향을 제공할 수 있다. 학습 중에 $x$가 $p_0 (x)$에 접근하는 동안 $t$가 작을수록 $p_t (x \vert y)$와 $p_0 (x \vert y)$ 사이의 간격이 좁아지고 $p_0 (x \vert y)$에 맞춰 정교한 디테일을 제공할 수 있다.

Mesh 표현과 fine-tuning

Mesh 텍스처를 표현하기 위해 NeRF 단계에서 상속된 좌표 기반 해시 그리드 인코더를 채택한다. Fantasia3D를 따라 먼저 normal map을 사용하여 형상을 최적화한 다음 텍스처를 최적화함으로써 형상과 텍스처의 최적화를 푼다. VSD를 사용하여 형상을 최적화하면 SDS를 사용하는 것보다 더 많은 디테일이 제공되지 않는다. 이는 mesh 해상도가 고주파수 디테일을 표현할 만큼 크지 않기 때문일 수 있다. 따라서 효율성을 위해 SDS를 사용하여 형상을 최적화한다. 그러나 Fantasia3D와 달리 본 논문의 텍스처 최적화는 CFG = 7.5의 VSD에서 annealed time schedule로 supervise되므로 SDS보다 더 많은 디테일을 제공할 수 있다.

Experiments

1. Results of ProlificDreamer

다음은 ProlificDreamer의 생성 결과이다.

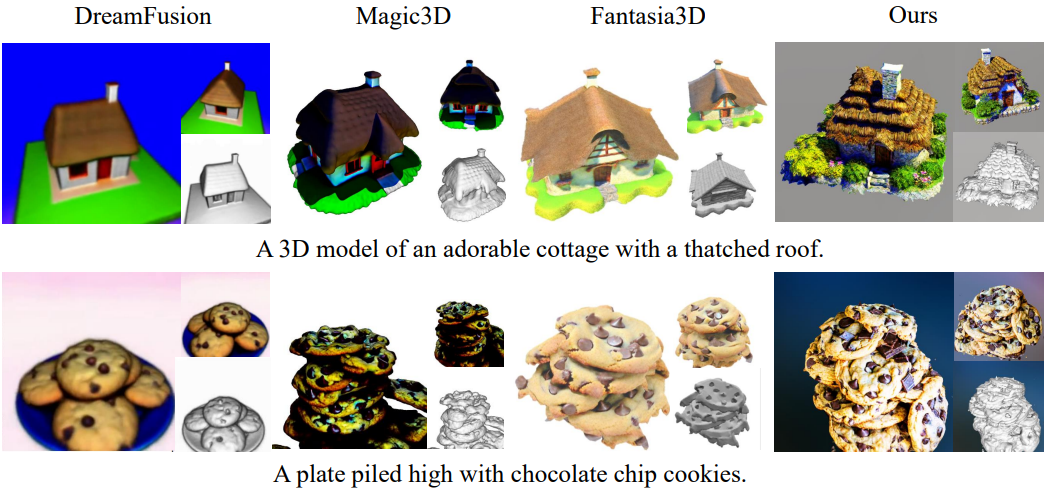
다음은 baseline들과의 비교 결과이다.

2. Ablation Study

다음은 높은 충실도의 NeRF 생성을 위한 개선점에 대한 ablation study 결과이다. 프롬프트는 “an elephant shull”이다.

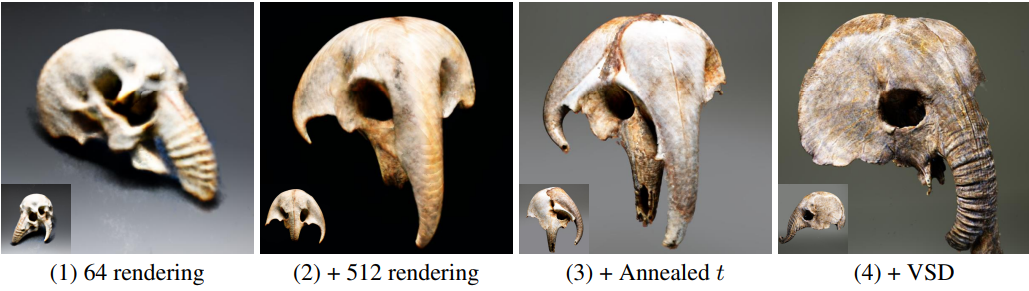
• (1): 64 렌더링 해상도와 SDS loss를 사용한 공통 설정
• (2): 렌더링 해상도를 512로 증가
• (3): Annealed time schedule 사용
• (4): VSD 적용

Limitations

생성에 몇 시간이 걸리며 이는 diffusion model에 의한 이미지 생성보다 훨씬 느리다. 장면 초기화를 통해 대규모 장면 생성이 가능하지만 학습 중 카메라 포즈는 장면 구조와 무관하므로 더 나은 디테일 사항 생성을 위해 장면 구조에 따라 적응형 카메라 포즈 범위를 고안하여 개선할 수 있다. 또한 다른 생성 모델과 마찬가지로 가짜 및 악성 콘텐츠를 생성하는 데 활용될 수 있으므로 더 많은 관심과 주의가 필요하다.