[논문리뷰] Polynomial Implicit Neural Representations For Large Diverse Datasets (Poly-INR)

CVPR 2023. [Paper] [Github]
Rajhans Singh, Ankita Shukla, Pavan Turaga
Arizona State University
20 Mar 2023

Introduction

가장 널리 알려진 생성 모델은 convolution 아키텍처를 기반으로 한다. 그러나 implicit neural representation (INR)과 같은 최근의 발전은 각 픽셀이 독립적으로 합성되는 좌표 위치의 연속 함수로 이미지를 나타낸다. 이러한 함수는 심층 신경망을 사용하여 근사화된다. INR은 좌표 격자를 사용하여 손쉬운 이미지 변환과 고해상도 업샘플링을 위한 유연성을 제공한다. 따라서 INR은 매우 적은 학습 이미지에서 3D 장면 재구성과 렌더링에 매우 효과적이다. 그러나 일반적으로 주어진 단일 장면, 신호 또는 이미지를 나타내도록 학습된다. 최근 INR은 전체 이미지 데이터셋을 생성하는 생성 모델로 구현되었다. 사람의 얼굴과 같이 완벽하게 선별된 데이터셋에서 CNN 기반 생성 모델과 비슷한 성능을 발휘한다. 그러나 아직 ImageNet과 같은 크고 다양한 데이터셋으로 확장되지 않았다.

INR은 일반적으로 위치 인코딩 모듈과 MLP로 구성된다. INR의 위치 인코딩은 Fourier feature라고 하는 sinusoidal function을 기반으로 한다. 몇몇 방법들은 sinusoidal positional encoding 없이 MLP를 사용하면 흐릿한 출력을 생성한며 저주파 정보만 보존한다는 것을 보여주었다. 그러나 MLP에서 ReLU activation을 주기적 또는 비주기적 activation function으로 대체하여 위치 인코딩을 제거할 수 있다. 그러나 INR 기반 GAN에서 MLP의 주기적 activation function을 사용하면 ReLU 기반 MLP를 사용한 위치 인코딩에 비해 성능이 떨어진다.

ReLU 기반 MLP는 더 높은 도함수에 포함된 정보를 캡처하지 못한다. 더 높은 미분 정보를 통합하지 못하는 것은 ReLU의 조각별 선형 특성 때문이며 ReLU의 2차 이상의 미분은 일반적으로 0이다. 이는 주어진 함수의 테일러 급수 전개로 더 해석될 수 있다. 함수의 고차 도함수 정보는 테일러 급수로부터 유도된 고차 다항식의 계수에 포함된다. 따라서 고주파 정보를 생성할 수 없는 것은 ReLU 기반 MLP 모델이 고차 다항식을 근사화하는 데 비효율적이기 때문이다.

MLP를 사용한 sinusoidal positional encoding이 널리 사용되었지만 이러한 INR의 용량은 두 가지 이유로 제한될 수 있다.

1. 임베딩 space의 크기가 제한된다. 따라서 주기적 함수의 유한하고 고정된 조합만 사용할 수 있으므로 더 작은 데이터셋으로 적용이 제한된다.
2. 이러한 INR 디자인은 수학적으로 일관성이 있어야 한다. 이러한 INR 모델은 주기 함수가 네트워크의 초기 부분을 정의하고 나중 부분이 ReLU 기반 비선형 함수인 주기 함수의 비선형 조합으로 해석될 수 있다. 이와 반대로 고전적인 변환 (푸리에 변환, 사인, 코사인)은 주기 함수의 선형 합산으로 이미지를 나타낸다. 그러나 신경망에서 위치 임베딩의 선형 조합만 사용하는 것도 제한적이어서 크고 다양한 데이터셋을 표현하기 어렵다.

따라서 본 논문은 주기 함수를 사용하는 대신 좌표 위치의 다항 함수로 이미지를 모델링한다.

다항식 표현의 주요 이점은 ImageNet과 같은 대규모 데이터셋을 나타내기 위해 MLP로 다항식 계수를 쉽게 parameterize할 수 있다는 것이다. 그러나 일반적으로 MLP는 저차 다항식만 근사화할 수 있다. 첫 번째 레이어에서 $x^p y^q$ 형식의 다항식 위치 임베딩을 사용하여 MLP가 고차에 근접하도록 할 수 있다. 그러나 이러한 디자인은 고정 임베딩 크기가 고정된 다항식 차수만 통합하기 때문에 제한적이다. 또한 주어진 이미지에 대한 각 다항식의 중요성을 미리 알지 못한다.

따라서 위치 인코딩을 사용하지 않고 MLP의 깊이에 따라 다항식의 차수를 점진적으로 증가시킨다. 모든 ReLU 레이어 후에 얻은 feature와 affine 변환된 좌표 위치 사이의 element-wise multiplication을 통해 이를 달성한다. Affine 파라미터는 알려진 분포에서 샘플링된 latent code에 의해 parameterize된다. 이러한 방식으로 네트워크는 필요한 다항식 순서를 학습하고 학습 가능한 파라미터가 상당히 적은 복잡한 데이터셋을 나타낸다.

Method

다음 형식으로 이미지를 나타내는 함수 클래스에 관심이 있다.

\[\begin{equation} G(x, y) = g_{00} + g_{10} x + g_{01} y + \ldots + g_{pq} x^p y^q \end{equation}\]

여기서 $(x, y)$는 크기 $H \times W$의 좌표 격자에서 샘플링된 정규화된 픽셀 위치이며 다항식의 계수 $g_{pq}$는 알려진 분포에서 샘플링된 latent 벡터 $z$에 의해 parameterize되며 픽셀 위치에 독립적이다. 따라서 이미지를 형성하기 위해 주어진 고정 $z$에 대해 모든 픽셀 위치 $(x, y)$에 대해 generator $G$를 평가한다.

\[\begin{equation} I = \{ G(x, y; z) \; \vert \; (x, y) \in \textrm{CoordinateGrid} (H, W) \} \\ \textrm{CoordinateGrid} (H, W) = \{ (\frac{x}{W-1}, \frac{y}{H-1} ) \; \vert \; 0 \le x < W, 0 \le y < H \} \end{equation}\]

서로 다른 latent 벡터 $z$를 샘플링하여 서로 다른 다항식을 생성하고 실제 이미지 분포에 대해 이미지를 나타낸다.

Linear layer와 ReLU layer만 사용하여 다항식을 학습하는 것이 목표이다. 그러나 MLP의 기존 정의는 일반적으로 소수의 Linear layer와 ReLU layer에서 처리되는 좌표 위치를 입력으로 사용한다. INR의 이 정의는 저차 다항식을 근사화할 수만 있으므로 저주파 정보만 생성한다. 그러나 $x^p y^q$ 형식의 다항식으로 구성된 위치 임베딩을 사용하여 고차 다항식을 근사화할 수 있다. 그러나 INR의 이 정의는 고정 크기의 임베딩 space가 다항식 차수의 작은 조합만 포함할 수 있기 때문에 제한적이다. 또한 이미지를 미리 생성하는 데 어떤 다항식 순서가 필수적인지 알 수 없다. 따라서 네트워크에서 다항식 차수를 점진적으로 증가시키고 필요한 차수를 학습하도록 한다.

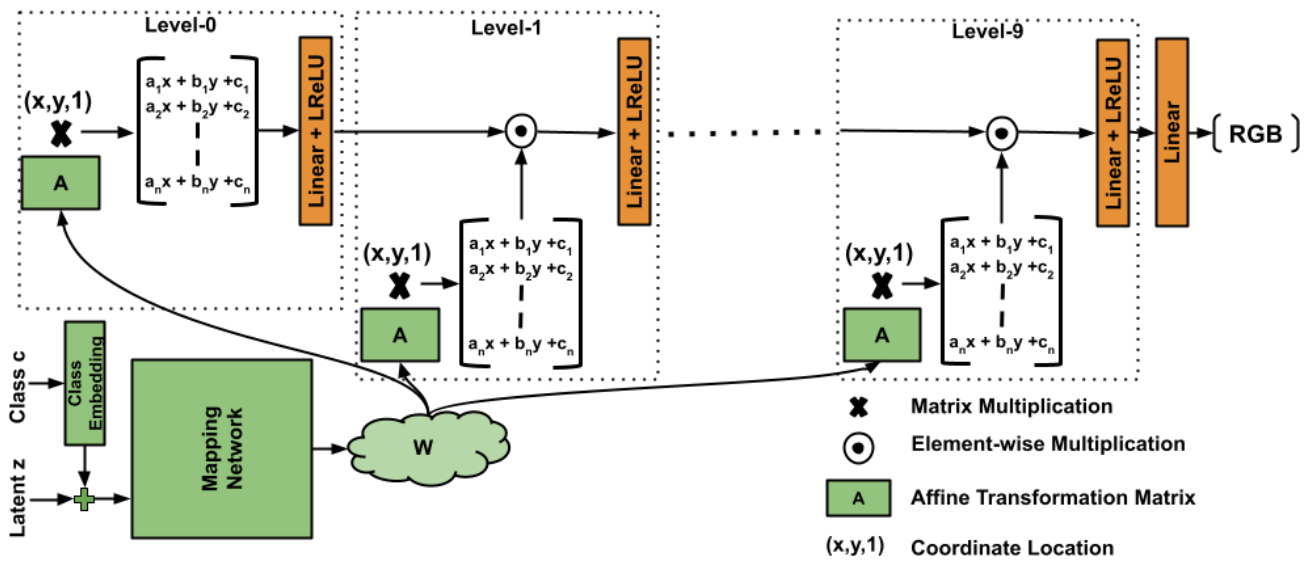
위 그림과 같이 서로 다른 레벨에서 affine 변환된 좌표 위치와 element-wise multiplication을 사용하여 이를 구현한다. 모델은 두 부분으로 구성된다.

1. Latent code $z$를 가져와 affine 파라미터 공간에 매핑하는 매핑 네트워크 $W$
2. 픽셀 위치를 가져와 해당 RGB 값을 생성하는 합성 네트워크

매핑 네트워크

매핑 네트워크는 latent code $z \in \mathbb{R}^{64}$를 가져와 $W \in \mathbb{R}^{512}$에 매핑한다. 모델은 StyleGAN-XL에서 사용된 매핑 네트워크를 채택한다. 그것은 one-hot 클래스 레이블을 512차원 벡터에 임베딩하고 이를 latent code $z$와 연결하는 사전 학습된 클래스 임베딩으로 구성된다. 그런 다음 매핑 네트워크는 $W$에 매핑하는 두 개의 레이어가 있는 MLP로 구성된다. 이 $W$를 사용하여 추가 linear layer를 사용하여 affine 파라미터를 생성한다. 따라서 $W$를 affine parameters space라고 부른다.

합성 네트워크

합성 네트워크는 주어진 픽셀 위치 $(x, y)$에 대한 RGB ($\mathbb{R}^3$) 값을 생성한다. 합성 네트워크는 여러 레벨로 구성된다. 각 레벨에서 매핑 네트워크와 픽셀 좌표 위치로부터 affine 변환 파라미터를 받는다. 레벨 0에서 좌표 격자를 affine 변환하고 Leaky-ReLU로 이어지는 Linear layer에 공급한다. 나중 레벨에서는 이전 레벨의 feature와 affine 변환된 좌표 격자 간에 element-wise multiplication을 수행한 다음 Leaky-ReLU로 이어지는 Linear layer에 공급한다. 각 레벨에서 element-wise multiplication을 통해 네트워크는 $x$ 또는 $y$ 좌표 위치의 차수를 늘리거나 affine 변환 계수 $a_j = b_j = 0$을 유지하여 차수를 늘리지 않는 유연성을 갖는다. 본 논문의 모델에서는 ImageNet과 같은 대규모 데이터셋을 생성하기에 충분한 10개의 레벨을 사용한다. 수학적으로 합성 네트워크는 다음과 같이 표현할 수 있다.

\[\begin{equation} G_\textrm{syn} = \ldots \sigma (W_2 ((A_2 X) \odot \sigma (W_1 ((A_1 X) \odot \sigma (W_0 (A_0 X)))))) \end{equation}\]

여기서 $X \in \mathbb{R}^{3 \times H \times W}$는 바이어스에 대한 추가 차원이 있는 크기 $H \times W$의 좌표 격자이고, $A_i \in \mathbb{R}^{n \times 3}$은 레벨 $i$에 대한 매핑 네트워크의 affine 변환 행렬, $W_i \in \mathbb{R}^{n \times n}$은 레벨 $i$에서 Linear layer의 가중치, $\sigma$는 Leaky-ReLU layer, $\odot$은 element-wise multiplication이다. 여기서 $n$은 합성 네트워크에서 feature 채널의 차원이며 모든 레벨에서 동일하다. ImageNet과 같은 큰 데이터셋의 경우 채널 차원 $n = 1024$를 선택하고 FFHQ와 같은 작은 데이터셋의 경우 $n = 512$를 선택한다. 이 정의에서 모델은 Linear layer와 ReLU layer를 end-to-end로만 사용하고 각 픽셀을 독립적으로 합성한다.

Relation to StyleGAN

StyleGAN은 본 논문의 공식화의 특별한 경우로 볼 수 있다. $x$와 $y$ 좌표 위치의 affine 변환 행렬에서 계수 ($a_j$, $b_j$)를 0으로 유지하면 바이어스 항 $c_j$가 스타일 코드로 작동한다. 그러나 affine 변환은 StyleGAN 모델의 모든 위치에 대해 동일한 스타일 코드를 사용하는 대신 스타일 코드에 위치 바이어스를 추가한다. 이 위치 바이어스는 특정 이미지 영역에만 스타일 코드를 적용할 때 모델을 매우 유연하게 만들어 표현력을 향상시킨다.

또한 본 논문의 모델은 많은 측면에서 StyleGAN과 다르다.

1. 본 논문의 방법은 가중치 변조/복조 또는 정규화 트릭을 사용하지 않는다.
2. 본 논문의 모델은 low-pass filter나 convolution layer를 사용하지 않는다.
3. 합성 네트워크에 공간 노이즈를 주입하지 않는다. 또한 이러한 트릭을 사용하여 모델의 성능을 더욱 향상시킬 수 있다.

Experiments

• 데이터셋: ImageNet, FFHQ
• 구현 디테일
  • StyleGAN-XL의 학습 방법을 따름
  • 사전 학습된 classifier (DeiT, EfficientNet)를 기반으로 하는 projected discriminator 사용
  • 추가 classifier guidance loss를 사용

1. Quantitative results

다음은 ImageNet에서 Poly-INR을 CNN 기반 방법들과 비교한 표이다.

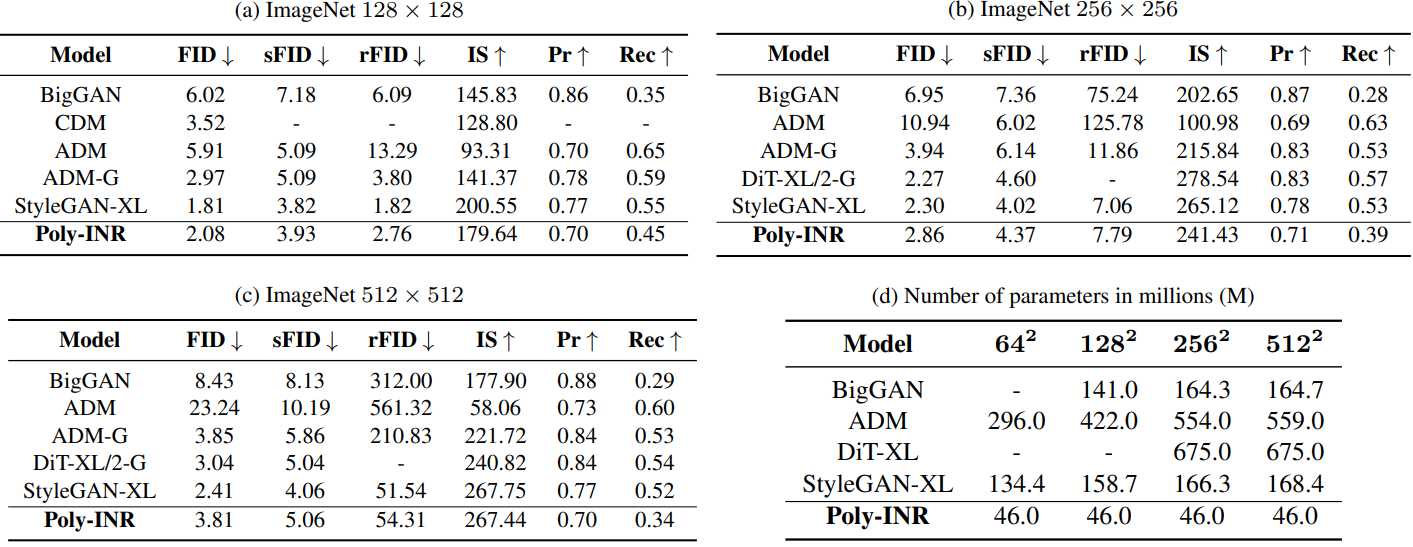
다음은 FFHQ 256$\times$256에서 Poly-INR을 CNN 기반 방법들과 비교한 표이다.

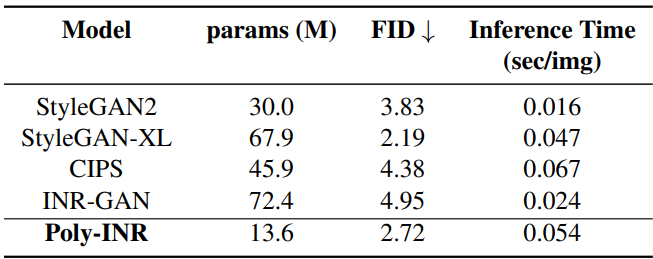
2. Qualitative results

다음은 다양한 해상도의 ImageNet에서 학습된 Poly-INR이 생성한 샘플들이다.

Heat-map visualization

다음은 합성 네트워크의 여러 레벨의 히트맵을 시각화한 것이다.

Extrapolation

다음은 이미지 경계 외부의 extrapolation을 보여주는 예시 이미지들이다.

Sampling at higher-resolution

다음은 낮은 해상도에서 학습된 모델을 512$\times$512에서 평가한 표이다.

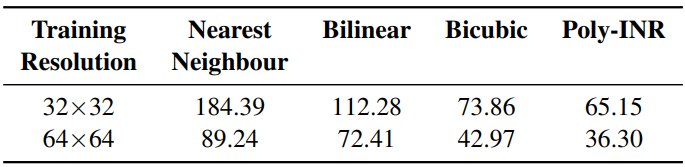
Interpolation

다음은 랜덤으로 샘플링된 두 이미지 사이에서의 부드러운 보간 결과이다.

Style-mixing

다음은 소스 이미지 A에서 소스 이미지 B로의 style mixing 예시이다.

Inversion

다음은 affine parameters space에 임베딩된 이미지들을 보간한 결과이다.

다음은 affine parameters space에 임베딩된 이미지들의 style mixing 결과이다.