[논문리뷰] 3D Shape Generation and Completion through Point-Voxel Diffusion (PVD)
ICCV 2021. [Paper] [Github] [Page]
Linqi Zhou, Yilun Du, Jiajun Wu
Stanford University | MIT
8 Apr 2021
Introduction

3D 형상의 생성 모델링은 비전, 그래픽, 로봇 공학 전반에 걸쳐 광범위한 응용이 가능하다. 이러한 하위 애플리케이션에서 좋은 성능을 발휘하려면 우수한 3D 생성 모델이 충실하고 확률적이어야 한다. 충실한 모델은 인간에게 사실적인 형상을 생성하고 깊이 맵과 같은 조건부 입력을 사용할 수 있는 경우 이러한 부분 관찰을 존중한다. 확률적 모델은 생성 문제와 completion 문제에 대한 미정의 multi-modal 특성을 캡처한다. 처음부터 또는 부분 관찰에서 다양한 형상을 샘플링하고 생성할 수 있다. 위에서 볼 수 있듯이 의자 등받이만 보이는 경우 좋은 생성 모델은 팔걸이가 있는 의자와 없는 의자를 포함하여 여러 개의 완성된 의자를 생성할 수 있어야 한다.
기존의 형상 생성 모델은 크게 두 가지 카테고리로 나눌 수 있다. 첫 번째는 2D 픽셀의 자연스러운 확장인 3D voxel에서 작동한다. Voxel은 사용하기 간단하지만 고차원으로 확장할 때 엄청나게 큰 메모리를 요구하므로 충실도가 높은 결과를 생성할 가능성이 낮다. 모델의 두 번째 클래스는 point cloud 생성을 연구하고 유망한 결과를 생성했다. 보다 충실하면서도 이러한 접근 방식은 일반적으로 point cloud 생성을 결정론적 인코더로 얻은 형상 인코딩을 조건으로 하는 point 생성 프로세스로 간주한다. 따라서 shape completion을 수행할 때 이러한 접근 방식은 completion 문제의 multi-modal 특성을 캡처할 수 없다.
최근 probabilistic diffusion models이라는 새로운 종류의 생성 모델이 2D 이미지 생성에서 인상적인 성능을 달성했다. 이러한 접근 방식은 denoising process에 대한 확률 모델을 학습한다. Diffusion model은 이미지와 같은 대상 출력에 대한 Gaussian noise를 점진적으로 제거하도록 supervise된다. DDPM과 같은 diffusion model은 확률적이며 매우 사실적인 2D 이미지를 생성한다.
그러나 diffusion model을 3D로 확장하는 것은 기술적으로 매우 중요하다. Voxel과 point 표현에 diffusion model을 직접 적용하면 생성 품질이 저하된다. 이는 첫째, 순수한 voxel이 binary이므로 diffusion model의 확률론적 특성에 적합하지 않기 때문이다. 둘째, point cloud는 모델에 실행 불가능한 제약을 부과하는 순열 불변성을 요구하다.
본 논문은 denoising diffusion model을 3D 형상의 하이브리드 point-voxel 표현과 결합하여 위의 문제를 해결하는 확률적이고 유연한 형상 생성 모델인 Point-Voxel Diffusion (PVD)를 제안한다. Point-voxel 표현은 구조화된 지역성을 point cloud 처리로 구축한다. Denoising diffusion model과 통합된 PVD는 Gaussian noise를 denoising하여 고품질 형상을 생성하고 부분 관찰로부터 여러 completion 결과를 생성하는 새롭고 확률적인 방법을 제안한다.
PVD의 고유한 강점은 unconditional한 형상 생성과 조건부 multi-modal shape completion을 위한 통합된 확률론적 공식이라는 것이다. Multi-modal shape completion은 디지털 디자인 또는 로봇 공학과 같은 어플리케이션에서 매우 바람직한 기능이지만 형상 생성에 대한 과거 연구에서는 주로 결정론적 형상 인코더와 디코더를 사용하여 voxel 또는 point cloud에서 가능한 단일 completion을 출력한다. 반대로 PVD는 통합 프레임워크에서 조건부 형상 생성과 조건부 shape completion을 모두 수행할 수 있으므로 목적 함수에 대한 최소한의 수정만 필요하다. 따라서 diffusion initialization에 따라 여러 completion 결과를 샘플링할 수 있다.
Point-Voxel Diffusion
1. Formulation
DDPM은 생성이 denoising process로 모델링되는 생성 모델이다. Gaussian noise에서 시작하여 날렵한 형상이 형성될 때까지 denoising을 수행한다. 특히, denoising process는 $x_T, x_{T-1}, \cdots, x_0$으로 표시되는 noise 레벨이 감소하는 일련의 형상 변수를 생성한다. 여기서 $x_T$는 Gaussian prior에서 샘플링되고 $x_0$는 최종 출력이다.
생성 모델을 학습시키기 위해 ground-truth diffusion 분포 $q(x_{0:T})$ (ground-truth 형상에 Gaussian noise를 점진적으로 추가하여 정의됨)를 정의하고 noise 손상 프로세스를 반전시키는 것이 목표인 diffusion model $p_\theta (x_{0:T})$를 학습시킨다. 두 확률 분포를 Markov transition 확률의 곱으로 분해한다.
\[\begin{equation} q(x_{0:T}) = q(x_0) \prod_{t=1}^T q(x_t \vert x_{t-1}) \\ p_\theta (x_{0:T}) = p(x_T) \prod_{t=1}^T p_\theta (x_{t-1} \vert x_t) \end{equation}\]$q(x_0)$는 데이터 분포이고 $p(x_T)$는 표준 Gaussian prior이다. $q(x_t \vert x_{t-1})$는 forward process이고 $q(x_{t-1} \vert x_t)$는 reverse process, $p_\theta (x_{t-1} \vert x_t)$는 생성 프로세스이다. 이 프로세스는 아래 그림과 같다.
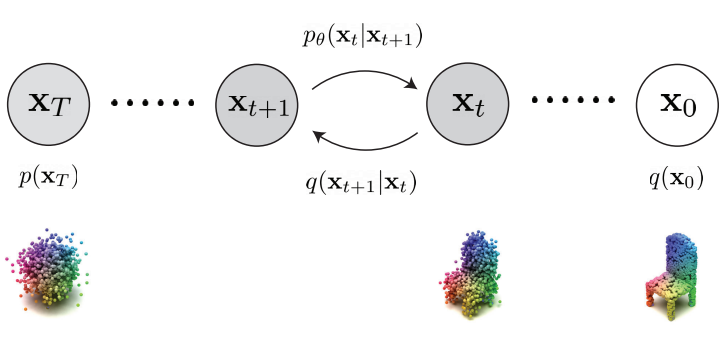
사전 정의된 Gaussian noise 값의 증가 수열 $\beta_1, \cdots, \beta_T$이 주어지면 각 transition 확률은 다음과 같이 정의된다.
$\mu_\theta (x_t, t)$는 timestep $t-1$에서 생성 모델의 예측된 형상을 나타낸다. 경험적으로 $\sigma_t^2 = \beta_t$로 설정하는 것이 잘 작동하였다고 한다. 직관적으로 forward process는 데이터에 점진적으로 더 많은 random noise를 주입하는 것으로 볼 수 있으며, 생성 프로세스는 reverse process를 모방하여 현실적인 샘플을 얻기 위해 점진적으로 노이즈를 제거한다고 볼 수 있다.
Training objective
Likelihood $p_\theta (x)$를 학습시키기 위해 모든 $x_0, \cdots, x_T$를 포함하는 log data likelihood의 variational lower bound를 최대화한다.
\[\begin{equation} \mathbb{E}_{q(x_0)} [\log p_\theta (x_0)] \ge \mathbb{E}_{q(x_{0:T})} \bigg[ \log \frac{p_\theta (x_{0:T})}{q(x_{1:T} \vert x_0)} \bigg] \end{equation}\]위의 목적 함수에서는 forward process $q(x_t \vert x_{t-1})$은 고정되고 $p(x_T)$는 Gaussian prior로 정의되므로 $\theta$의 학습에 영향을 미치지 않는다. 따라서 최종 목적 함수는 joint posterior $q(x_{1:T} \vert x_0)$을 사용하여 전체 데이터 likelihood가 주어지면 maximum likelihood로 줄일 수 있다.
\[\begin{equation} \max_\theta \mathbb{E}_{x_0 \sim q(x_0), x_{1:T} \sim q(x_{1:T} \vert x_0)} \bigg[ \sum_{t=1}^T \log p_\theta (x_{t-1} \vert x_t) \bigg] \end{equation}\]$q(x_{1:T} \vert x_0)$는 $q(x_{t-1} \vert x_t, x_0)$의 곱으로 인수분해할 수 있다. 각 ground-truth posterior $q(x_{t-1} \vert x_t, x_0)$는 수치적으로 tractable하며, 다음과 같이 가우시안 분포로 parameterize할 수 있다.
\[\begin{equation} q(x_{t-1} \vert x_t, x_0) = \mathcal{N} \bigg( \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_0 + \frac{\sqrt{\alpha_t} (1 - \bar{\alpha_{t-1}})}{1 - \bar{\alpha}_t} x_t, \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t I \bigg) \\ \alpha_t = 1 - \beta_t, \quad \bar{\alpha}_t = \prod_{s=1}^t \alpha_s \end{equation}\]이 속성은 각 timestep이 독립적으로 학습할 수 있게 한다.
$p_\theta (x_{t-1} \vert x_t)$와 $q(x_{t-1} \vert x_t, x_0)$이 모두 가우시안이므로 모델을 출력 noise로 reparameterize할 수 있고 최종 loss는 모델 출력 $\epsilon_\theta (x_t, t)$와 noise $\epsilon$ 사이의 $\mathcal{L}_2$ loss로 줄일 수 있다.
\[\begin{equation} \| \epsilon - \epsilon_\theta (x_t, t) \|^2, \quad \epsilon \sim \mathcal{N} (0, I) \end{equation}\]직관적으로, 모델은 3D 형상을 손상시키는 데 필요한 noise 벡터를 예측하려고 한다.
Point cloud는 $p_\theta (x_{t-1} \vert x_t)$에서 점진적으로 샘플링하여 생성할 수 있다.
\[\begin{equation} x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \bigg( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (x_t, t) \bigg) + \sqrt{\beta_t} z, \quad z \sim \mathcal{N} (0,I) \end{equation}\]2. Shape Completion
목적 함수는 주어진 부분 형상이 주어진 조건부 생성 모델을 학습하도록 간단하게 수정할 수 있다. Point cloud 샘플을 $x_0 = (z_0, \tilde{x}_0)$로 나타내며, $z_0 \in \mathbb{R}^{M \times 3}$은 고정된 부분 형상이다. 그런 다음 조건부 forward process를 정의할 수 있다.
\[\begin{equation} q(\tilde{x}_t \vert \tilde{x}_{t-1}, z_0) := \mathcal{N} (\sqrt{1 - \beta_t} \tilde{x}_{t-1}, \beta_t I) \\ p_\theta (\tilde{x}_{t-1} \vert \tilde{x}_t, z_0) := \mathcal{N} (\mu_\theta (x_t, z_0, t), \sigma_t^2 I) \\ \end{equation}\]위 식은 free point $\tilde{x}_t$의 forward 및 생성 transition 확률을 나타내며, $z_0$는 모든 timestep에서 바뀌지 않는다. 직관적으로, 이 프로세스는 unconditional한 생성과 동일하며 부분 형상 $z_0$는 고정되고 빠진 부분만 diffuse한다.
수정된 목적 함수는 부분 형상 $z_0$로 컨디셔닝된 likelihood도 최대화한다.
\[\begin{equation} \mathbb{E}_{(\tilde{x}_0, z_0) \sim q(x_0), x_{1:T} \sim q(x_{1:T} \vert \tilde{x}_0, z_0)} \bigg[ \sum_{t=1}^T \log p_\theta (\tilde{x}_{t-1} \vert \tilde{x}_t, z_0) \bigg] \end{equation}\]각 posterior $q(\tilde{x}_{t-1} \vert \tilde{x}_t, \tilde{x}_0, z_0)$는 unconditional 생성 모델과 비슷하게 유도할 수 있다. 같은 이유로 비슷한 $\mathcal{L}_2$ loss를 구성할 수 있다.
\[\begin{equation} \mathcal{L}_t = \| \epsilon - \epsilon_\theta (\tilde{x}_t, z_0, t) \|^2 \end{equation}\]또한, 부분 형상이 항상 고정되어 있으므로 $z_0$에 영향을 미치는 모델 출력의 부분 집합을 마스킹하고 \(\tilde{\epsilon}(\tilde{x}_t, z_0, t)\)와 \(\tilde{x}_t\)에만 영향을 미치는 random noise 사이의 L2 거리를 최소화할 수 있다. 실제로 모델에 $z_0$와 $x_t$를 입력하고 \(x_{t-1}\)을 얻는다. 여기서 부분 집합 \(\tilde{x}_{t-1}\)만이 L2 loss에 사용된다. Shape completion에서 \(\tilde{x}_{t-1}\)은 $z_0$과 연결되어 다시 모델에 대한 입력이 된다. 이를 통해 정확히 동일한 학습 아키텍처가 단순히 목적 함수를 변경하여 생성과 shape completion를 모두 수행할 수 있다.
Experiments
1. Shape Generation
다음은 1-NN을 metric으로 사용하여 baseline과 생성 결과를 비교한 표이다.
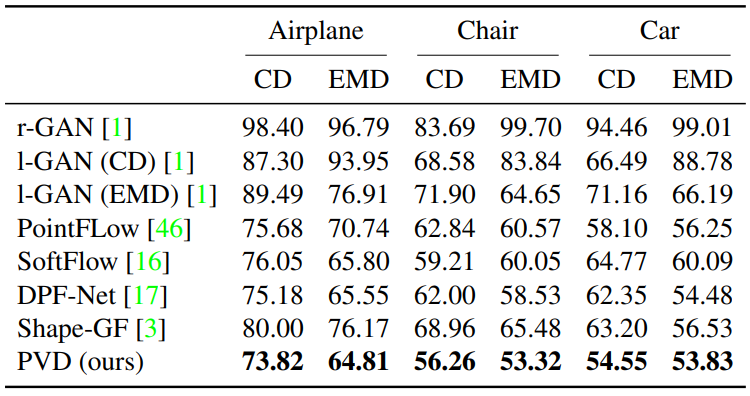
다음은 2048개의 point로 unconditional하게 생성한 형상을 나타낸 것이다.

2. Shape Completion
다음은 baseline과의 정량적 평가를 나타낸 표이다.
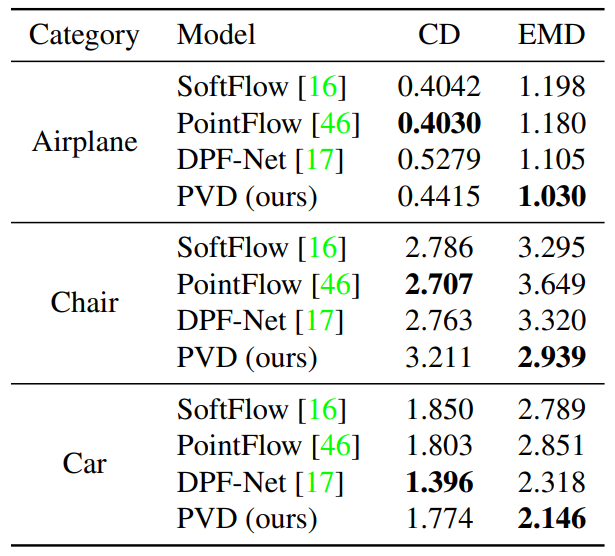
다음은 shape completion을 시각화한 것이다.

다음은 CD가 baseline보다 높은 전형적인 케이스로, 입력 view가 ground-truth 형상을 대부분 모르는 경우다. CD는 1000이 곱해진 값이고 EMD는 100이 곱해진 값이다.

Baseline model은 이러한 비정상적인 각도를 만났을 때 평균 모양을 출력하는 경향이 있다. 당연히 평균 모양은 그림에 예시된 것처럼 다른 모양보다 더 자주 ground-truth에 더 가깝다. 그러나 PVD는 평균 모양보다 ground-truth에서 더 멀리 떨어져 있을 수 있지만 부분 형상과 잘 일치하는 가능한 completion을 찾는다. 보여지는 예시에서 PVD의 completion은 세단이 아닌 밴이지만 똑같이 현실적이다.
3. Multi-Modal Completion
다음은 PartNet에 대한 multi-modal completion의 정량적 비교 표이다.
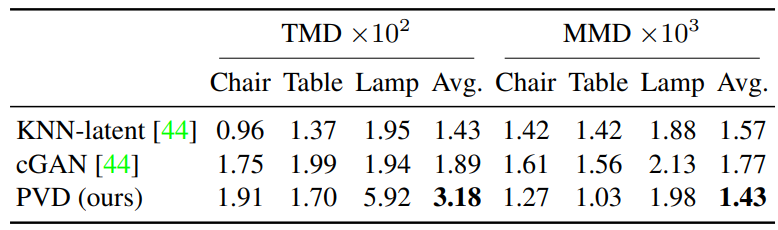
다음은 PartNet에 대한 multi-modal completion의 시각적 비교를 나타낸 것이다.

다음은 ShapeNet에 대한 multi-modal completion 결과이다.

다음은 Redwood 3DScans 데이터셋의 스캔에 PVD를 적용한 결과이다.
