[논문리뷰] Point-NeRF: Point-based Neural Radiance Fields

CVPR 2022 Oral. [Paper] [Page] [Github]
Qiangeng Xu, Zexiang Xu, Julien Philip, Sai Bi, Zhixin Shu, Kalyan Sunkavalli, Ulrich Neumann
University of Southern California | Adobe Research
21 Jan 2022

Introduction

NeRF는 neural radiance field를 모델링하여 novel view synthesis (NVS)에서 큰 성공을 거두었다. NeRF는 ray marching을 통해 전체 공간에 대한 글로벌 MLP를 사용하여 radiance field를 재구성한다. 이는 느린 장면당 MLP 학습과 광대한 빈 공간에 대한 불필요한 샘플링으로 인해 재구성 시간이 길어진다.

본 논문은 이 문제를 3D neural point을 사용하여 연속적인 radiance field를 모델링하는 새로운 포인트 기반 radiance field 표현인 Point-NeRF를 사용하여 해결하였다. 순전히 장면별 fitting에 의존하는 NeRF와 달리 Point-NeRF는 장면 전체에 걸쳐 사전 학습된 MLP를 통해 효과적으로 초기화할 수 있다. 게다가 PointNeRF는 실제 장면 형상을 근사하는 고전적인 point cloud를 활용하여 빈 공간에서의 ray sampling을 피한다. Point-NeRF의 이러한 장점은 더 효율적인 재구성과 더 정확한 렌더링으로 이어진다.

Point-NeRF 표현은 포인트별 feature가 있는 point cloud로 구성된다. 각 neural point는 주변의 로컬 3D 장면 형상과 외형을 인코딩한다. 이전의 포인트 기반 렌더링 기술은 유사한 neural point cloud를 사용하지만 이미지 공간에서 작동하는 rasterization과 2D CNN으로 렌더링을 수행하였다. Point-NeRF는 대신 이러한 neural point를 MLP로 처리하여 미분 가능한 ray marching을 통해 고품질 렌더링을 가능하게 하는 연속적인 radiance field를 모델링한다. 특히, 모든 3D 위치에 대해 MLP 네트워크를 사용하여 해당 위치에서 volume density와 뷰에 따른 radiance를 얻기 위해 주변 지역의 neural point들을 집계한다. 이를 통해 연속적인 radiance field를 표현할 수 있다.

저자들은 포인트 기반 radiance field를 효율적으로 초기화하고 최적화하기 위한 학습 기반 프레임워크를 제시하였다. 초기 필드를 위해 multi-view stereo (MVS) 기술을 활용한다. 즉, cost volume 기반 네트워크를 적용하여 깊이를 예측한 다음 3D 공간에 unprojection한다. 또한 CNN을 학습하여 입력 이미지에서 2D feature map을 추출하고 자연스럽게 포인트별 feature를 제공한다. 여러 뷰의 neural point들은 neural point cloud로 결합되어 포인트 기반 radiance field를 형성한다. 이 포인트 생성 모듈을 포인트 기반 볼륨 렌더링 네트워크로 end-to-end로 학습하여 새로운 뷰에서의 이미지를 렌더링하고 실제 값으로 supervise한다. 이를 통해 inference 시에 포인트 기반 radiance를 직접 예측할 수 있는 일반화 가능한 모델이 생성된다. 예측이 완료되면 초기 포인트 기반 필드가 짧은 시간 내에 장면별로 추가로 최적화되어 사실적인 렌더링을 달성한다.

내장된 point cloud 재구성을 사용하는 것 외에도 다른 재구성 기술의 point cloud를 기반으로 radiance field를 생성할 수도 있다. 그러나 COLMAP과 같은 기술로 재구성된 point cloud는 실제로 최종 렌더링에 부정적인 영향을 미치는 구멍과 outlier들을 포함한다. 이 문제를 해결하기 위해 최적화 프로세스의 일부로 point growing과 point pruning을 도입하였다. 볼륨 렌더링 중 기하학적 추론을 활용하고 volume density가 높은 영역의 point cloud 경계 근처의 포인트를 성장시키고 volume density가 낮은 영역에서 포인트를 pruning한다. 이 메커니즘은 최종 재구성 및 렌더링 품질을 효과적으로 개선한다.

Point-NeRF Representation

볼륨 렌더링과 radiance field

물리 기반 볼륨 렌더링은 미분 가능한 ray marching을 통해 수치적으로 평가할 수 있다. 구체적으로, 픽셀의 radiance는 픽셀을 통해 ray marching하고, 광선상의 $M$개의 shading 포인트 \(\{x_j\}_{j=1}^M\)를 샘플링하고, volume density를 사용하여 radiance를 누적하여 계산할 수 있다.

\[\begin{equation} c = \sum_M \tau_j (1 - \exp (- \sigma_j \Delta_j)) r_j, \quad \tau_j = \exp (- \sum_{t=1}^{j-1} \sigma_t \Delta_t) \end{equation}\]

($\tau$는 투과율, $\sigma_j$는 포인트 $j$의 volume density, $r_j$는 $j$의 radiance, $\Delta_t$는 인접한 샘플 간의 거리)

Radiance field는 모든 3D 위치에서 $\sigma$와 $r$을 나타낸다. NeRF는 이러한 radiance field를 학습하기 위해 MLP를 사용한다. 본 논문은 대신 볼륨 속성을 계산하기 위해 neural point cloud를 활용하여 더 빠르고 고품질의 렌더링을 달성하였다.

포인트 기반 radiance field

Neural point cloud는 $P = {(p_i, f_i, \gamma_i)}_{i=1}^N$로 나타낼 수 있다. $p_i$는 각 포인트 $i$의 위치, $f_i$는 로컬 장면 콘텐츠를 인코딩하는 feature 벡터, $\gamma_i$는 실제 장면 표면 근처에 해당 포인트가 위치할 가능성을 나타내는 신뢰도 값이다. 이 point cloud에서 radiance를 예측한다.

3D 위치 $x$가 주어지면, 특정 반경 내에서 그 주변의 $K$개의 이웃 neural point를 쿼리한다. 포인트 기반 radiance field는 volume density $\sigma$와 뷰 방향 $d$에 대한 radiance $r$을 모든 shading 위치 $x$의 이웃 neural point에서 예측하는 신경망으로 추상화될 수 있다.

\[\begin{equation} (\sigma, r) = \textrm{Point-NeRF} (x, d, p_1, f_1, \gamma_1, \ldots, p_K, f_K, \gamma_K) \end{equation}\]

이를 위해 여러 개의 하위 MLP가 있는 신경망을 사용한다. 전반적으로, 먼저 각 neural point에 대한 MLP 처리를 수행한 다음 여러 neural point의 정보를 집계하여 최종 추정치를 얻는다.

포인트별 처리

다음과 같이 shading 위치 $x$에 대한 feature 벡터를 예측하기 위해 각 이웃 neural point를 처리하기 위해 MLP $F$를 사용한다.

\[\begin{equation} f_{i,x} = F (f_i, x - p_i) \end{equation}\]

Feature $f_i$는 $p_i$ 주변의 로컬 3D 장면 콘텐츠를 인코딩한다. 상대적 위치 $x - p_i$를 사용하면 네트워크가 translation에 대해 invariant하게 되어 더 나은 일반화가 가능하다.

뷰에 따른 radiance regression

이러한 $K$개의 이웃 포인트에 대한 feature $f_{i,x}$를 집계하여 $x$에서의 장면 외형을 설명하는 하나의 feature $f_x$를 얻기 위해 inverse-distance 가중치를 사용한다.

\[\begin{equation} f_x = \sum_i \gamma_i \frac{w_i}{\sum w_i} f_{i,x}, \quad \textrm{where} \; w_i = \frac{1}{\| p_i - x \|} \end{equation}\]

그러면 MLP $R$은 뷰 방향 $d$가 주어진 $f_x$에서 뷰에 따른 radiance를 예측한다.

\[\begin{equation} r = R (f_x, d) \end{equation}\]

Inverse-distance 가중치 $w_i$를 사용하여 더 가까운 포인트가 shading 계산에 더 많이 기여하도록 한다. 또한, 이 프로세스에서 포인트별 신뢰도 $\gamma$를 사용한다. 이는 최종 재구성에서 sparsity loss로 최적화되어 네트워크에 불필요한 포인트를 거부하는 유연성을 제공한다.

Density regression

$x$에서 volume density $\sigma$를 계산하기 위해 비슷하게 여러 포인트를 집계한다. 그러나 먼저 MLP $T$를 사용하여 포인트별 density $\sigma_i$를 예측한 다음 다음과 같은 inverse-distance 기반으로 가중치를 부여한다.

\[\begin{equation} \sigma_i = T (f_{i,x}), \quad \sigma = \sum_i \sigma_i \gamma_i \frac{w_i}{\sum w_i} \end{equation}\]

따라서 각 neural point는 volume density에 직접적으로 기여하고, 신뢰도 $\gamma_i$는 이 기여와 명시적으로 연관된다. $\gamma_i$를 포인트 제거 프로세스에 활용한다.

Point-NeRF Reconstruction

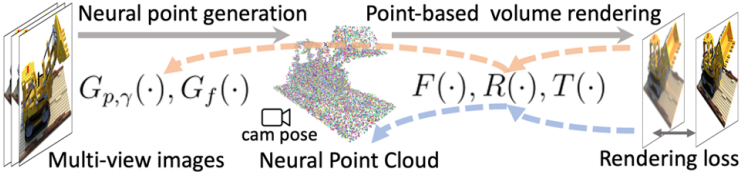
1. Generating initial point-based radiance fields

이미지 $I_1, \ldots, I_Q$와 포인트 클라우드가 주어지면, 랜덤하게 초기화된 포인트별 feature와 MLP를 렌더링 loss로 최적화하여 Point-NeRF 표현을 재구성할 수 있다. 그러나 이 단순한 장면별 최적화는 기존 포인트 클라우드에 따라 달라지며 엄청나게 느릴 수 있다. 따라서 효율적인 재구성을 위해 신경망을 통해 포인트 위치 $p_i$, feature $f_i$, 신뢰도 $\gamma_i$를 포함한 모든 neural point 속성을 예측하는 생성 모듈을 제안하였다. 네트워크의 직접 추론은 좋은 초기 포인트 기반 radiance field를 출력한다. 그런 다음 초기 radiance field를 fine-tuning하여 고품질 렌더링을 달성할 수 있다. 매우 짧은 기간 내에 렌더링 품질이 NeRF보다 더 좋거나 동일하며 최적화하는 데 훨씬 더 오랜 시간이 걸린다.

포인트 위치와 신뢰도

Cost volume 기반 3D CNN을 사용하여 3D 포인트 위치를 생성하기 위해 MVS를 활용한다. 이러한 3D CNN들은 고품질의 dense한 형상을 생성하고 도메인 간에 잘 일반화된다. 시점 $q$에서 카메라 파라미터가 $\Phi_q$인 각 입력 이미지 $I_q$에 대해 MVSNet을 따라 먼저 이웃 시점의 2D 이미지 feature를 워핑하여 plane-swept cost volume을 구축한 다음 3D CNN을 사용하여 깊이 확률 볼륨을 추정한다. Depth map은 확률로 가중된 평면당 깊이 값을 선형 결합하여 계산된다. Depth map을 3D 공간으로 unprojection하여 시점 $q$별 포인트 클라우드 \(\{p_1, \ldots, p_{N_q}\}\)를 얻었다.

깊이 확률은 포인트가 표면에 있을 가능성을 설명하므로 깊이 확률 볼륨을 tri-linear로 샘플링하여 각 $p_i$에서 신뢰도 $\gamma_i$를 얻는다.

\[\begin{equation} \{p_i, \gamma_i\} = G_{p, \gamma} (I_q, \Phi_q, I_{q_1}, \Phi_{q_1}, I_{q_2}, \Phi_{q_2}, \ldots) \end{equation}\]

(\(G_{p, \gamma}\): MVSNet 기반 네트워크, \(I_{q_1}, \Phi_{q_1}, \ldots\): 추가 이웃 시점)

Point features

2D CNN $G_f$를 사용하여 각 이미지 $I_q$에서 2D feature map을 추출한다. Feature map은 \(G_{p, \gamma}\)의 깊이 예측과 정렬되며 포인트별 feature $f_i$를 직접 예측하는 데 사용된다.

\[\begin{equation} \{f_i\} = G_f (I_q) \end{equation}\]

구체적으로, 3개의 다운샘플링 레이어가 있는 VGG 네트워크 아키텍처를 $G_f$로 사용한다. $f_i$로 다른 해상도의 중간 feature를 결합하여 멀티스케일 장면 외형을 모델링하는 의미 있는 포인트 설명을 제공한다.

End-to-end 재구성

최종 뉴럴 포인트 클라우드를 얻기 위해 여러 시점에서 포인트 클라우드를 결합한다. 렌더링 loss를 사용하여 end-to-end로 표현 네트워크들과 함께 포인트 생성 네트워크를 학습시킨다. 이를 통해 생성 모듈은 합리적인 초기 radiance field를 생성할 수 있다. 또한 Point-NeRF 표현에서 MLP를 합리적인 가중치로 초기화하여 장면별 fitting 시간을 크게 절약한다.

또한 전체 생성 모듈을 사용하는 것 외에도 파이프라인은 COLMAP과 같은 다른 접근 방식에서 재구성된 포인트 클라우드를 사용하는 것을 지원하며, 이 경우 MVS 네트워크를 제외한 모델은 여전히 ​​각 포인트에 대해 의미 있는 초기 feature를 제공할 수 있다.

2. Optimizing point-based radiance fields

위의 파이프라인은 새로운 장면에 대한 합리적인 초기 포인트 기반 radiance field를 출력할 수 있다. 미분 가능한 ray marching을 통해 특정 장면에 뉴럴 포인트 클라우드와 MLP를 최적화하여 radiance field를 더욱 개선할 수 있다.

초기 포인트 클라우드, 특히 외부 재구성 방법 (ex. Metashape, COLMAP)의 포인트 클라우드는 종종 렌더링 품질을 저하시키는 구멍과 outlier들을 포함할 수 있다. 이 문제를 해결하기 위해 기존 포인트의 위치를 ​​직접 최적화하면 학습이 불안정해지고 큰 구멍을 채울 수 없다. 대신, 형상 모델링과 렌더링 품질을 점진적으로 개선하는 새로운 point pruning과 point growing 기술을 적용한다.

Point pruning

신뢰도 값을 사용하여 불필요한 outlier들을 제거한다. 포인트의 신뢰도는 포인트별 기여도와 직접 관련이 있다. 결과적으로 낮은 신뢰도는 점의 로컬 영역에서 낮은 volume density를 반영하여 비어 있음을 나타낸다. 따라서 1만 iteration마다 $\gamma_i < 0.1$인 포인트들을 제거한다.

또한 신뢰도에 sparsity loss를 부과하여 신뢰도 값을 0 또는 1에 가깝게 강제한다.

\[\begin{equation} \mathcal{L}_\textrm{sparse} = \frac{1}{\vert \gamma \vert} \sum_{\gamma_i} [\log (\gamma_i) + \log (1 - \gamma_i)] \end{equation}\]

장면별 최적화 단계에서는 L2 렌더링 loss와 sparsity loss를 결합하는 loss function을 채택하였다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{render} + \alpha \mathcal{L}_\textrm{sparse} \end{equation}\]

Point growing

본 논문은 추가로 원래 포인트 클라우드에서 누락된 장면 형상을 커버하기 위해 새로운 포인트를 키우는 새로운 기술을 제안하였다. 기존 포인트의 정보를 직접 활용하는 pruning과 달리, 포인트를 키우려면 포인트가 없는 빈 영역에서 정보를 복구해야 한다. 따라서 Point-NeRF 표현으로 모델링된 로컬 형상을 기반으로 포인트 클라우드 경계 근처에서 점진적으로 포인트를 키운다.

Ray marching에서 샘플링된 광선별 셰이딩 위치를 활용하여 새로운 포인트 후보를 식별한다. 구체적으로, 광선을 따라 가장 높은 불투명도를 가진 셰이딩 위치 $x_{j_g}$를 찾는다.

\[\begin{equation} \alpha_j = 1 - \exp (-\sigma_j \Delta_j), \quad j_g = \underset{j}{\arg \max} \alpha_j \end{equation}\]

$\epsilon_{j_g}$를 $x_{j_g}$의 가장 가까운 neural point까지의 거리라고 했을 때, \(\alpha_{j_g} > T_\textrm{opacity}\)이고 \(\epsilon_{j_g} > T_\textrm{dist}\)이면 $x_{j_g}$에서 neural point를 키운다. 이는 위치가 표면 근처에 있지만 다른 neural point와 거리가 멀다는 것을 의미한다. 이 point growing 전략을 반복함으로써 초기 포인트 클라우드에서 누락된 영역을 포함하도록 확장할 수 있다.

Point growing은 특히 sparse한 COLMAP과 같은 방법으로 재구성된 포인트 클라우드에 유리하다. 포인트 클라우드가 초기에 1,000개에 불과한 극단적인 경우에도 point growing을 통해 점진적으로 새로운 포인트를 성장시키고 표면을 합리적으로 커버할 수 있다.

Experiments

• 구현 디테일
  • 네트워크
    • 주파수 위치 인코딩을 상대적 위치와 각 포인트의 feature에 적용하여 네트워크 $G_f$에 사용하고, 시점 방향에 적용하여 네트워크 $R$에 사용
    • $G_f$에서 서로 다른 해상도의 세 레이어에서 멀티스케일 이미지 feature를 추출하여 8+16+32=56개의 채널을 가진 벡터를 구성
    • 뷰에 따라 달라지는 효과를 처리하기 위해 뷰 방향 (3차원)을 추가하여 최종 포인트별 neural feature는 59채널 벡터
  • 학습
    • 먼저 MVSNet 기반 깊이 생성 네트워크를 GT depth로 학습 후 전체 파이프라인을 end-to-end로 학습
    • $\alpha$ = 0.002

1. Evaluation

다음은 DTU 데이터셋에서 기존 방법들과 비교한 결과이다.

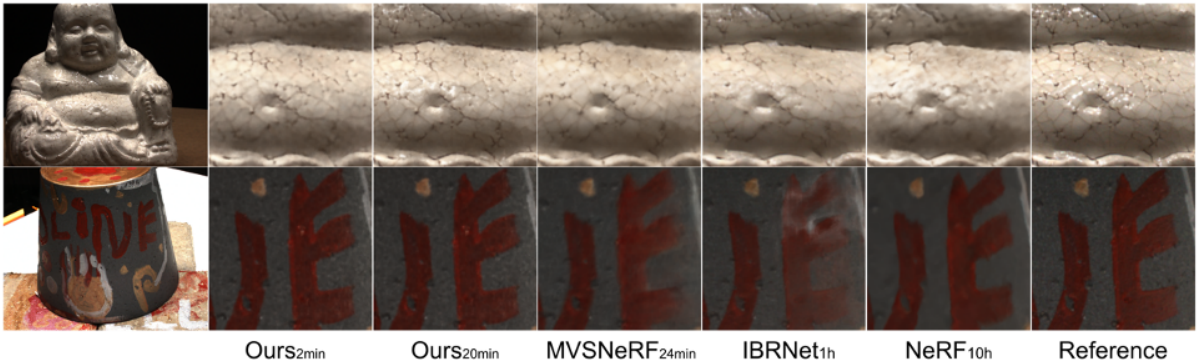
다음은 Synthetic-NeRF 데이터셋에서 기존 방법들과 비교한 결과이다.

다음은 Tanks & Temples과 ScanNet에서 NSVF와 비교한 표이다.

2. Additional experiments

다음은 point pruning과 point growing 유무에 대한 최적화 결과를 비교한 것이다.

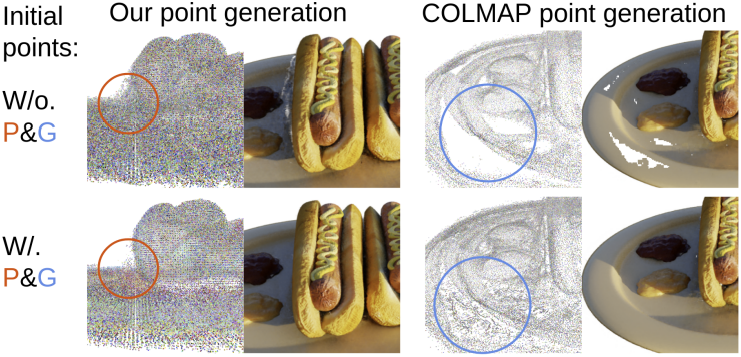
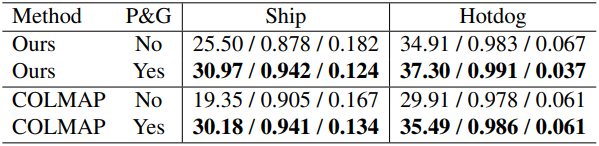
다음은 랜덤하게 샘플링한 1,000개의 COLMAP 포인트에서 시작하여 최적화한 예시이다.