Diffusion은 신이고 GPT는 무적이다

CVPR 2025 (Highlight). [Paper] [Page]
Bin Tan, Rui Yu, Yujun Shen, Nan Xue
Ant Group | University of Louisville
4 Dec 2024

Introduction

이미지 기반 평면 3D 재구성은 대부분 키포인트 기반 3D 재구성 파이프라인을 따르며, 평면을 특수한 유형의 visual feature로 처리한다. 그러나 이미지 공간에서 로컬 point feature와 평면 마스크 간의 본질적인 차이로 인해 기존 접근법은 평면 표현의 장점을 충분히 활용하지 못하며, 일반적으로 매우 대략적이고 장면의 많은 디테일을 잃는다.

본 논문의 주요 아이디어는 멀티뷰 입력 이미지로부터 얻은 3D planar primitive들을 이용하여 실내 장면을 근사하고, 이를 통해 일관된 3D 평면을 갖도록 직접 최적화하는 것이다. 본 논문에서는 3D 공간에서 직사각형 planar primitive를 2.5D depth map과 normal map으로 미분 가능하게 splatting하여 명시적으로 최적화하는 PlanarSplatting을 도입하였다. 잘 설계된 평면 splatting 함수 덕분에, PlanarSplatting은 monocular depth와 monocular normal 효과적으로 활용하여 정확한 평면 최적화를 구현하였다. 평면 주석 없이 유사한 3D planar primitive들을 병합하여 최종 고품질 평면 표면을 재구성할 수 있다.

PlanarSplatting은 3D planar primitive를 기반으로 직접 설계되고 CUDA를 통해 효율적으로 구현되므로, 최신 Gaussian Splatting (GS) 기법과 완벽하게 통합되어 고품질의 실내 novel view synthesis (NVS)를 구현할 수 있다. 빠르고 정확한 장면 재구성을 통해 GS 기반 기법은 densification 없이도 효과적으로 초기화 및 최적화될 수 있으며, 이를 통해 더 나은 렌더링 결과와 현저히 단축된 학습 시간을 얻을 수 있다.

Method

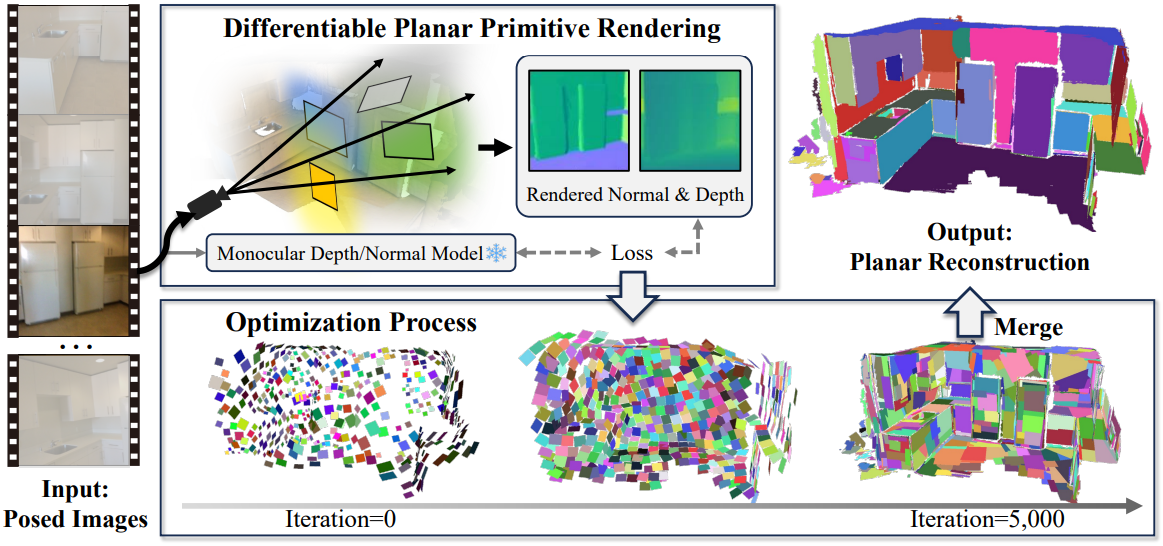
1. Learnable Planar Scene Representation

학습 가능한 planar primitive


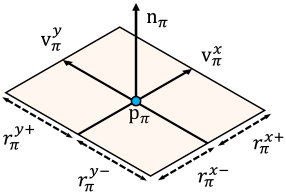
Planar primitive $\pi$를 평면 중심 \(\textbf{p}_\pi \in \mathbb{R}^3\), 평면 회전 \(\textbf{q}_\pi \in \mathbb{R}^4\) (quaternion 표현), 평면 반지름 \(\textbf{r}_\pi\)를 포함한 여러 학습 가능한 파라미터를 갖는 3차원 직사각형으로 정의한다. 특히, 평면 형상의 최적화 유연성을 향상시키기 위해 \(\textbf{r}_\pi\)를 다음과 같이 정의한다.

\[\begin{equation} \textbf{r}_\pi = \{ r_\pi^{x+}, r_\pi^{x-}, r_\pi^{y+}, r_\pi^{y-} \} \in \mathbb{R}_{+}^4 \end{equation}\]

(\(r_\pi^{x+}, r_\pi^{x-}, r_\pi^{y+}, r_\pi^{y-}\)는 직사각형의 X축/Y축의 +/- 방향으로 정의된 반지름)

3D planar primitive의 X축과 Y축의 양의 방향을 직교하는 두 개의 단위 벡터 \(\textbf{v}_\pi^x, \textbf{v}_\pi^y \in \mathbb{R}^3\)로 정의한다.

\[\begin{equation} \textbf{v}_\pi^x = \textbf{R}(\textbf{q}_\pi) [1,0,0]^\top, \quad \textbf{v}_\pi^y = \textbf{R}(\textbf{q}_\pi) [0,1,0]^\top \end{equation}\]

(\(\textbf{R}(\textbf{q}_\pi) \in \mathbb{R}^{3 \times 3}\)은 quaternion \(\textbf{q}_\pi\)의 회전 행렬)

마찬가지로, planar primitive의 normal \(\textbf{n}_\pi \in \mathbb{R}^3\)은 다음과 같이 계산할 수 있다.

\[\begin{equation} \textbf{n}_\pi = \textbf{R}(\textbf{q})[0,0,1]^\top \end{equation}\]

이러한 학습 가능한 파라미터들을 사용하면 3D planar primitive를 잠재적인 장면 표면에 맞춰 이동시킬 수 있으며, 최적화 중에 표면 모양에 맞게 변형시킬 수 있다.

장면 초기화

최적화 초기에 3D planar primitive를 빠르게 초기화하기 위해 monocular depth를 사용한다. 구체적으로, Metric3Dv2의 깊이를 사용하여 매우 대략적인 장면 형상을 얻는다. 그런 다음, 대략적인 메쉬에서 2,000개의 점을 무작위로 샘플링하여 3D planar primitive의 평면 중심을 얻는다. 각 primitive의 초기 반지름은 이웃하는 primitive 중 $\pi$에 가장 가까운 거리의 절반으로 설정한다. 대략적인 메쉬의 normal 방향을 사용하여 평면 회전을 초기화한다.

2. Differentiable Planar Primitive Rendering

광선-평면 교점

3D planar primitive를 2D 이미지 공간에 투영하기 위해, 먼저 planar primitive와 이미지 픽셀에서 나오는 광선 사이의 교점을 계산한다. 구체적으로, 카메라 중심 $\textbf{o} \in \mathbb{R}^3$에서 출발하여 방향이 $\textbf{d} \in \mathbb{R}^3$인 광선 \(\textbf{r} = \{\textbf{o}, \textbf{d}\}\)가 주어졌을 때, 이 광선과 planar primitive $\pi$의 교점 \(\textbf{x}_\pi^\textbf{r} \in \mathbb{R}^3\)은 다음과 같이 계산된다.

\[\begin{equation} \textbf{x}_\pi^\textbf{r} = \textbf{o} + \frac{(\textbf{p}_\pi - \textbf{o}) \cdot \textbf{n}_\pi}{\textbf{d} \cdot \textbf{n}_\pi} \textbf{d} \end{equation}\]
평면 Splatting 함수

광선-평면 교점 \(\textbf{x}_\pi^\textbf{r}\)를 구한 후, 렌더링에 사용될 평면 splatting 함수를 사용하여 splatting 가중치를 계산한다.

Gaussian 기반 splatting 함수는 planar primitive의 경계를 모호하게 만들어 재구성 품질을 저하시킨다.

따라서, 새로운 직사각형 기반 평면 splatting 함수를 사용하여 splatting 가중치를 계산한다. \(\textbf{x}_\pi^\textbf{r}\)에 대해, 먼저 $\pi$의 X축과 Y축에 대한 projection 거리 \(\mathcal{P}_X, \mathcal{P}_Y \in \mathbb{R}\)을 다음과 같이 계산한다.

\[\begin{equation} \mathcal{P}_X = (\textbf{x}_\pi^\textbf{r} - \textbf{p}_\pi) \cdot \textbf{v}_\pi^x, \quad \mathcal{P}_X = (\textbf{x}_\pi^\textbf{r} - \textbf{p}_\pi) \cdot \textbf{v}_\pi^y \end{equation}\]

그런 다음, 평면 $\pi$의 X축과 Y축을 따라 splatting 가중치 $w_X$와 $w_Y$를 다음과 같이 계산한다.

\[\begin{aligned} w_X (\textbf{x}_\pi^\textbf{r}) &= \begin{cases} 2 \sigma (5 \lambda (r_\pi^{x+} - \vert \mathcal{P}_X \vert)), & \textrm{if} \; \mathcal{P}_X > 0 \\ 2 \sigma (5 \lambda (r_\pi^{x-} - \vert \mathcal{P}_X \vert)), & \textrm{otherwise} \end{cases} \\ w_Y (\textbf{x}_\pi^\textbf{r}) &= \begin{cases} 2 \sigma (5 \lambda (r_\pi^{y+} - \vert \mathcal{P}_Y \vert)), & \textrm{if} \; \mathcal{P}_Y > 0 \\ 2 \sigma (5 \lambda (r_\pi^{y-} - \vert \mathcal{P}_Y \vert)), & \textrm{otherwise} \end{cases} \end{aligned}\]

최종 splatting 가중치는 다음과 같이 계산된다.

\[\begin{equation} w (\textbf{x}_\pi^\textbf{r}) = \begin{cases} w_X, & \textrm{if} \; w_X < w_Y \\ w_Y, & \textrm{otherwise} \end{cases} \end{equation}\]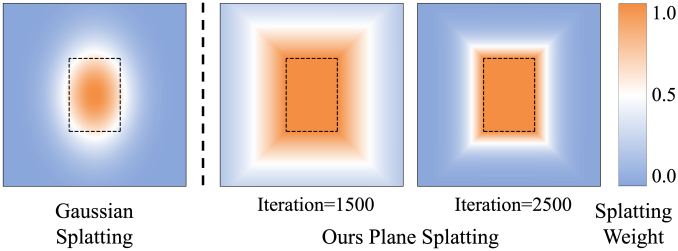


위 그림에서 볼 수 있듯이, hyperparameter $\lambda$가 증가함에 따라 평면 splatting 함수가 직사각형 planar primitive의 모양에 점차 근접한다. 실제로 최적화 과정에서 지수 함수를 사용하여 $\lambda$ 값을 최대값인 300까지 증가시킨다.

\[\begin{equation} \lambda = \textrm{min}(20 e^{-(1 - 0.001 \cdot \textrm{ite})}, 300) \end{equation}\]

($\textrm{ite}$는 최적화 과정의 iteration 번호)

블렌딩

모든 광선-평면 교점에 대해 splatting 가중치가 0.0001보다 낮은 평면을 필터링한 후, 나머지 교점을 깊이에 따라 가까운 교점에서 먼 교점 순으로 정렬한다. 그런 다음, 각 광선의 가장 가까운 교점 $M$를 선택하여 렌더링한다 (본 논문에서는 $M = 30$). 특정 이미지 $\textbf{I}$의 depth map과 normal map을 다음과 같이 렌더링한다.

\[\begin{equation} \textbf{D}_\textrm{render}^\Pi (\textbf{r}) = \sum_{j=1}^M T_j w (\textbf{x}_{\pi_{\tau(j)}}^\textrm{r}) t_j, \quad \textbf{N}_\textrm{render}^\Pi (\textbf{r}) = \sum_{j=1}^M T_j w (\textbf{x}_{\pi_{\tau(j)}}^\textrm{r}) \textbf{n}_{\pi_{\tau(j)}} \\ \textrm{where} \quad T_j = \prod_{i=1}^{j-1} (1 - w (\textbf{x}_{\pi_{\tau(i)}}^\textrm{r}) ) \end{equation}\]

($\tau (j)$는 평면의 인덱스, $t_j$는 교점의 depth)

Metric3Dv2로 예측한 depth map $\textbf{D}\textrm{pre}$과 Omnidata로 예측한 normal map $\textbf{N}\textrm{pre}$로 각각 렌더링된 depth map과 normal map을 학습시킨다. 렌더링 loss는 다음과 같다.

\[\begin{aligned} \mathcal{L}_\textrm{render}^\Pi &= \alpha_1 \sum_{\textbf{r} \in \textbf{I}} \| 1 - \textbf{N}_\textrm{render}^\Pi (\textbf{r})^\top \textbf{N}_\textrm{pre} (\textbf{r}) \|_1 \\ &+ \alpha_1 \sum_{\textbf{r} \in \textbf{I}} \| \textbf{N}_\textrm{render}^\Pi (\textbf{r}) - \textbf{N}_\textrm{pre} (\textbf{r}) \|_1 \\ &+ \alpha_2 \sum_{\textbf{r} \in \textbf{I}} \| \textbf{D}_\textrm{render}^\Pi (\textbf{r}) - \textbf{D}_\textrm{pre} (\textbf{r}) \|_1 \end{aligned}\]

3. Optimization

평면 분할

저자들은 최적화 과정에서 장면 형상에 더 잘 맞도록 평면의 반지름 기울기에 따라 분할 연산을 도입하였다. 평면의 X축에 대한 평균 반지름 기울기($r^{x+}$, $r^{x-}$)가 0.2보다 크면 Y축을 따라 평면을 분할한다. 마찬가지로, Y축에 대한 평균 반지름 기울기($r^{y+}$, $r^{y-}$)가 0.2보다 크면 X축을 따라 평면을 분할한다. 분할 연산은 1,000 iteration마다 수행된다.

평면 병합

최적화 후, normal 각도 오차가 25° 미만이고 offset 거리 차이가 0.1cm 미만인 학습된 3D planar primitive들을 병합한다. 여기서 offset은 장면 중심에서 평면 표면까지의 projection 거리를 의미한다.

Experiments

  • 데이터셋: ScanNetV2, ScanNet++
  • 학습 디테일
    • optimizer: Adam
    • iteration: 5,000
    • loss 가중치: \(\alpha_1 = 5.0\), \(\alpha_2 = 1.0\)

1. Comparisons with Baselines

다음은 (위) ScanNetV2와 (아래) ScanNet++에서의 평면 재구성 결과를 정량적으로 비교한 것이다. (“P. Ann.”은 학습에 평면 주석을 사용한 경우)


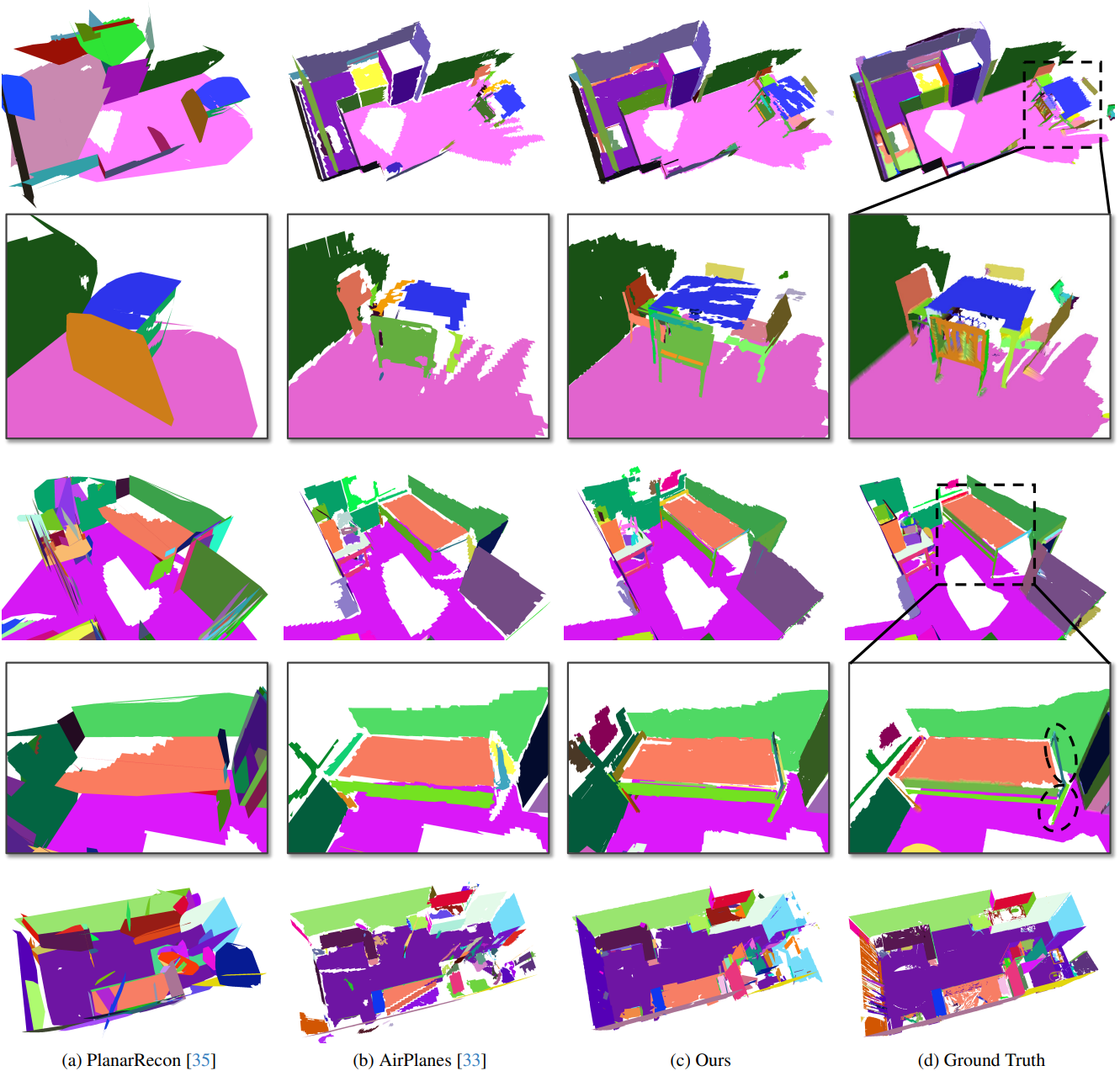
다음은 정성적 비교 결과이다.

2. Ablation Studies

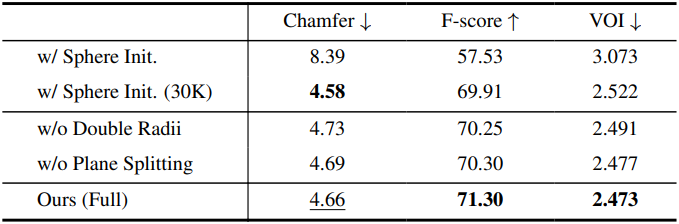
다음은 ablation study 결과이다.

3. PlanarSplatting for Novel View Synthesis

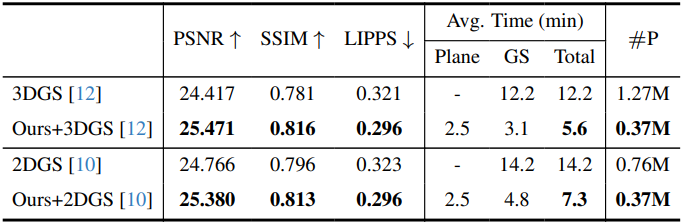
다음은 PlanarSplatting으로 3DGS와 2DGS를 초기화하여 novel view synthesis를 수행한 결과이다.

Limitations

곡면 등 복잡한 형상에는 적합하지 않다.

You may also enjoy