[논문리뷰] PhysDiff: Physics-Guided Human Motion Diffusion Model
ICCV 2023 (Oral). [Paper] [Page]
Ye Yuan, Jiaming Song, Umar Iqbal, Arash Vahdat, Jan Kautz
NVIDIA
5 Dec 2022
Introduction
딥 러닝 기반의 인간 모션 생성은 애니메이션, 게임, 가상 현실 등 수많은 응용 분야에서 중요한 task이다. 텍스트-모션 합성과 같은 일반적인 설정에서는 인간 동작의 multi-modal 분포를 캡처할 수 있는 조건부 생성 모델을 학습해야 한다. 분포는 매우 다양한 인간 동작과 인체 부위 간의 복잡한 상호 작용으로 인해 매우 복잡할 수 있다.
Denoising diffusion model은 이미지 생성 도메인에서 광범위하게 입증된 복잡한 분포를 모델링하는 강력한 능력으로 인해 이 task에 특히 적합한 생성 모델 클래스이다. 이러한 모델은 높은 test likelihood로 표시되는 강력한 mode coverage를 나타낸다. 또한 GAN에 비해 학습 안정성이 우수하고 VAE나 normalizing flow에 비해 샘플 품질이 우수하다. 최근에는 모션 생성 성능에서 표준 생성 모델을 훨씬 능가하는 모션 diffusion model을 제안했다.
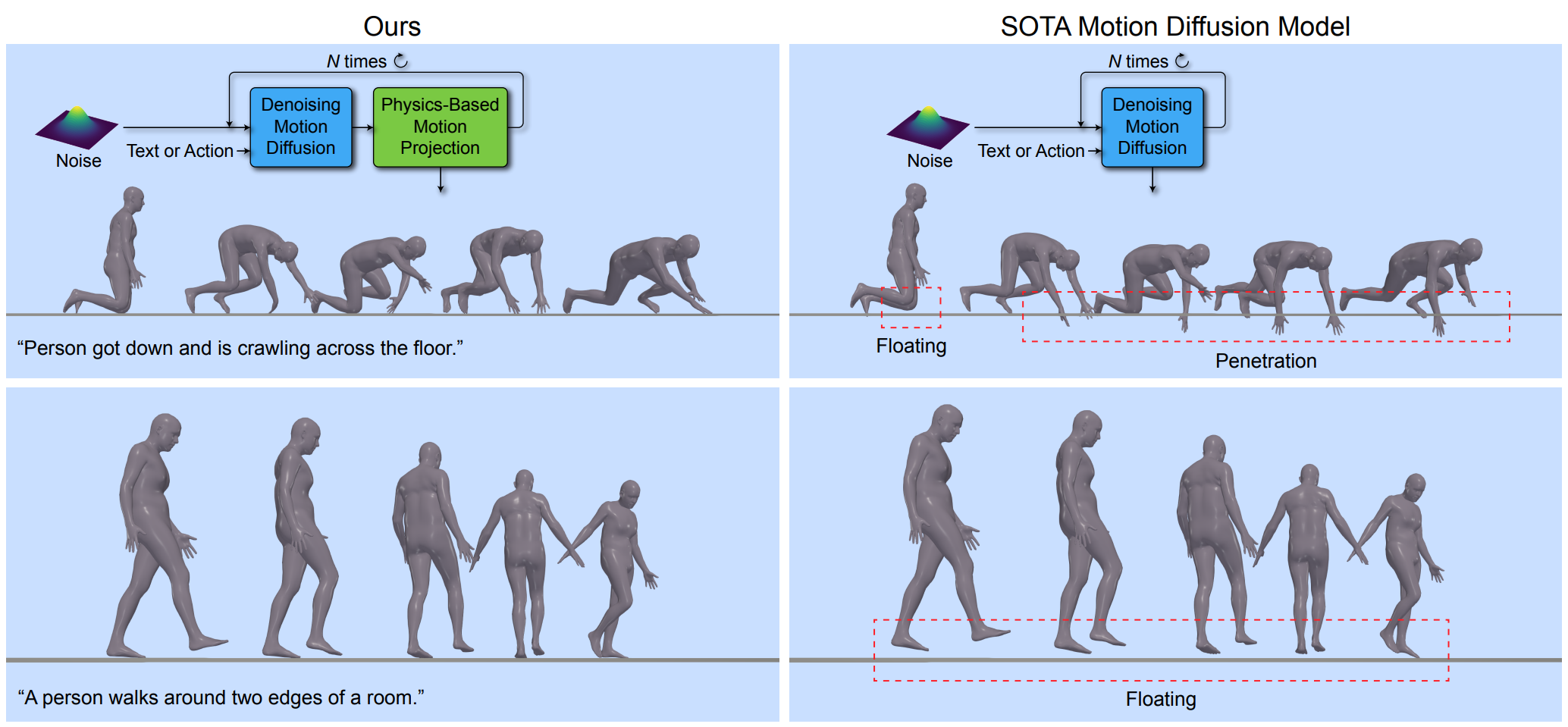
그러나 기존 모션 diffusion model은 인간 모션의 한 가지 필수 측면인 기본 물리 법칙을 간과한다. Diffusion model은 인간 동작의 분포를 모델링할 수 있는 뛰어난 능력을 가지고 있지만 여전히 물리적 제약을 적용하거나 힘과 접촉에 의해 유도된 복잡한 역학을 모델링하는 명확한 메커니즘이 없다. 결과적으로 생성된 모션은 공중에 떠 있거나 (floating) 발이 미끄러지거나 (foot sliding) 신체가 지면을 뚫고 들어가는 등 (ground penetration) 현저한 아티팩트가 포함되는 경우가 많다. 이는 물리적 부정확성에 매우 민감한 애니메이션이나 가상 현실과 같은 많은 실제 어플리케이션을 심각하게 방해한다. 이에 비추어 볼 때 해결해야 할 중요한 문제는 인간 모션 diffusion model이 물리 법칙을 반영하도록 만드는 것이다.
이 문제를 해결하기 위해 저자들은 denoising process에 물리 법칙을 주입하는 새로운 physics-guided motion diffusion model (PhysDiff)을 제안한다. 특히, PhysDiff는 물리적으로 가능한 space에 입력 모션을 project하는 물리 기반 모션 프로젝션 모듈을 활용한다. Diffusion process에서 모션 프로젝션 모듈을 사용하여 denoise된 diffusion step의 모션을 물리적으로 그럴듯한 모션으로 project한다. 이 새로운 모션은 denoising diffusion process를 guide하기 위해 다음 diffusion step에서 추가로 사용된다.
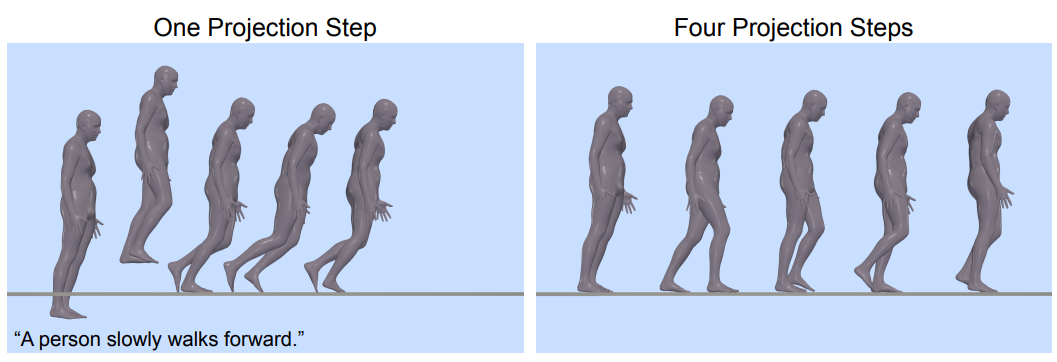
Diffusion process의 마지막에 물리 기반 프로젝션만 추가하고 싶을 수도 있다. 그러나 이것은 denoise된 모션이 너무 물리적으로 타당하지 않아 하나의 물리 기반 projection step으로 수정할 수 없기 때문에 부자연스러운 움직임을 생성할 수 있다 (위 그림 참고). 대신 diffusion process에 projection을 포함하고 물리와 diffusion을 반복적으로 적용하여 모션을 데이터 분포에 가깝게 유지하면서 물리적으로 타당한 space로 이동해야 한다.
물리 기반 모션 프로젝션 모듈은 PhysDiff에서 물리적 제약을 강제하는 중요한 역할을 하며, 이는 물리 시뮬레이터에서 모션 모방을 통해 달성된다. 특히, 대규모 모션 캡처 데이터를 사용하여 시뮬레이터에서 캐릭터 에이전트를 제어할 수 있는 모션 모방 정책을 학습하여 광범위한 입력 모션을 모방한다. 그 결과 시뮬레이션된 동작은 물리적 제약을 적용하고 아티팩트를 제거한다. 일단 학습되면 모션 모방 정책을 사용하여 diffusion step의 denoise된 모션을 모방하여 물리적으로 그럴듯한 모션을 출력할 수 있다.
Method
텍스트나 액션 레이블같은 조건 정보 $c$가 주어지면, 길이가 $H$인 물리적으로 그럴듯한 모션 \(x^{1:H} = \{x^h\}_{h=1}^H\)를 생성하는 것이 목표이다. 생성된 모션의 각 포즈 $x^h \in \mathbb{R}^{J \times D}$은 $J$개의 joint의 $D$ 차원 feature로 표현된다. $x_T^{1:H}$에서 시작하여 PhysDiff는 denoising 분포
\[\begin{equation} q (x_s^{1:H} \vert x_t^{1:H}, \mathcal{P}_\pi, c) \end{equation}\]를 모델링하며, 이 분포는 timestep $t$에서 $s$로 모션을 denoise한다. 모델을 반복적으로 적용하면 모션의 noise가 제거되어 최종 출력 $x^{1:H}$가 되는 깨끗한 모션 $x_0^{1:H}$이 된다. 모델의 중요한 구성 요소는 물리적 제약을 적용하는 물리 기반 모션 프로젝션 모듈 $\mathcal{P}_\pi$이다. 이 모듈은 모션 모방 정책 $\pi$를 활용하여 물리 시뮬레이터에서 diffusion step의 denoise된 모션을 모방하고 시뮬레이션된 모션을 사용하여 diffusion process를 추가로 guide한다.
1. Physics-Guided Motion Diffusion
Motion Diffusion
표기를 단순화하기 위해 때때로 조건 $c$에 대한 명시적 종속성을 생략한다. 항상 특정 조건 $c$로 diffusion model을 학습시킬 수 있다. Unconditional인 경우에도 범용 null 토큰 $\emptyset$로 모델을 컨디셔닝할 수 있다.
$p_0 (x)$를 데이터 분포라고 하면 시간 종속 분포의 $p_t (x_t)$의 시퀀스를 정의한다. 여기서 $\sigma_t$는 $\sigma_0 = 0$이고 $\sigma_T$는 데이터의 표준 편차보다 훨씬 크도록 정의한 시간에 따라 증가하는 noise 레벨의 시퀀스이다. 일반적으로 diffusion model은 $t = T$에서 $t = 0$까지 다음과 같은 SDE를 풀어 샘플을 추출한다.
\[\begin{equation} dx = - (\beta_t + \dot{\sigma_t}) \sigma_t \nabla_x \log p_t (x) dt + \sqrt{2 \beta_t} \sigma_t d \omega_t \end{equation}\]여기서 $\nabla_x \log p_t (x)$는 score function이고 $\omega_t$는 standard Wiener process이다. $\beta_t$는 주입되는 stochastic noise의 양을 조절하며, $\beta_t = 0$이면 SDE가 ODE가 된다. Score function의 중요한 속성은 주어진 $x_t$에 대하여 $x$의 minimum mean squared error (MMSE) estimator를 복구한다는 것이다.
\[\begin{equation} \tilde{x} := \mathbb{E} [x \vert x_t] = x_t + \sigma_t^2 \nabla_{x_t} \log p_t (x_t) \end{equation}\]여기서 $\tilde{x}$는 $x_t$의 “denoised” 버전으로 생각할 수 있다. $x_t$와 $\sigma_t$를 샘플링 중에 알기 때문에 역으로 $\tilde{x}$에서 $\nabla_{x_t} \log p_t (x_t)$를 얻을 수 있다.
Diffusion model은 score function을 다음과 같은 denoising autoencoder 목적 함수로 근사한다.
\[\begin{equation} \mathbb{E}_{x \sim p_0 (x), t \sim p(t), \epsilon \sim p(\epsilon)} [\lambda (t) \| x - D (x + \sigma_t \epsilon, t, c) \|_2^2] \end{equation}\]여기서 $D$는 denoiser이고, $p(t)$는 시간을 샘플링하는 분포이며 $\lambda (t)$는 loss weighting factor이다. $D$의 최적해는 MMSE estimator를 복구한 것이다.
Denoising diffusion model이 학습된 후, SDE나 ODE를 푸는 데 적용할 수 있다. 특정 접근 방식인 DDIM은 Algorithm 1과 같이 주어진 시간 $t$에서 시간 $s (s < t)$로 샘플 $x_t$를 한 step 업데이트를 수행한다.

직관적으로 샘플 $x_s$는 가우시안 분포에서 생성되며, $x_s$의 평균은 $x_t$와 $\tilde{x}$ 사이의 선형 보간이고 분산은 hyperparameter $\eta \in [0, 1]$에 의존한다. 특히 $\eta = 0$이면 DDPM을 따르고 $\eta = 1$이면 DDIM을 따른다. 저자들은 PhysDiff에서 $\eta = 0$이 더 성능이 좋다는 것을 발견했다. 위의 샘플링 과정이 일반적이므로 $x^{1:H}$에도 적용할 수 있다. 샘플링 중에 조건 $c$를 통합하기 위해서 classifier 기반 guidance나 classifier-free guidance를 사용할 수 있다.
Applying Physical Constraints.
인간 모션을 위한 기존의 diffusion model은 물리적 제약을 따르는 데이터에서 학습될 필요가 없었으며, 필요하다고 해도 denoiser network의 근사 오차와 샘플링 프로세스의 stochastic한 점 때문에 모션 샘플이 여전히 물리적으로 가능한 지 보장할 수 없었다. 마지막 모션 샘플이 물리적으로 그럴듯하도록 직접 수정할 수 있지만 수정 이후에도 모션의 물리적 오차가 너무 컸으며 여전히 이상적이지 않았다.
이 문제를 해결하기 위해 diffusion model이 목표 출력의 중간 추정 $\tilde{x}^{1:H}$를 생성한다는 사실을 이용하며, 마지막 step뿐만 아니라 중간 step에도 물리적 제약을 적용한다. 구체적으로, 물리 기반 모션 프로젝션 $\mathcal{P}_\pi : \mathbb{R}^{H \times J \times D} \rightarrow \mathbb{R}^{H \times J \times D}$를 원본 모션 $\tilde{x}^{1:H}$를 물리적으로 그럴듯한 모션 $\hat{x}^{1:H}$으로 매핑하는 모듈로 사용한다.
$\mathcal{P}_\pi$이 프로젝션이므로 반복적으로 적용하는 것이 모션을 개선하지 않는다.
\[\begin{equation} \mathcal{P}_\pi (\mathcal{P}_\pi (\tilde{x}^{1:H})) = \mathcal{P}_\pi (\tilde{x}^{1:H}) \end{equation}\]제안된 $\mathcal{P}_\pi$를 denoising diffusion 샘플링 프로세스에 통합하며, Algorithm 2와 같다.

DDIM sampler와 다른 부분은 추가적인 물리 기반 프로젝션을 수행하는 부분이다. PhysDiff는 다양한 신경망을 사용하는 denoiser $D$에 따라 다를 수 있다. PhysDiff의 물리 기반 프로젝션은 inference 시에도 적용되며, 이것이 PhysDiff가 일반적으로 다른 사전 학습된 모션 diffusion model과 호환할 수 있게 해준다. 즉, PhysDiff는 학습 없이 기존 diffusion model의 물리적 개연성을 개선하는 데 사용할 수 있다.
물리 시뮬레이션을 사용하기 때문에 프로젝션 $\mathcal{P}_\pi$는 다소 비용이 많이 들고 모든 diffusion timestep에서 프로젝션을 수행하는 것은 불가능하다. 따라서 수행할 물리 기반 프로젝션 step의 수가 제한되어 있는 경우 특정 timestep을 다른 timestep보다 우선시해야 한다.
여기서 저자들은 diffusion noise가 높을 때 물리 프로젝션을 수행하지 말아야 한다고 주장한다. 이는 denoiser $D$가 디자인상 $\tilde{x}^{1:H} = \mathbb{E}[x^{1:H} \vert x_t^{1:H}]$를 제공하며, 조건 $x_t^{1:H}$가 거의 정보를 포함하지 않을 때 $\tilde{x}^{1:H}$가 높은 noise 레벨에 대한 학습 데이터의 평균에 가깝기 때문이다. 경험적으로 평균 모션은 모드에 평균이 취해지기 때문에 몸의 움직임이 적어지며, 이는 분명히 물리적으로 그럴듯하지 못하다. 이러한 물리적으로 잘못된 모션을 물리 기반 프로젝션으로 수정하면 모션이 데이터 분포에서 더 멀어지고 diffusion process가 방해된다.
2. Physics-Based Motion Projection
Physics-guided diffusion process의 필수 요소 중 하나는 물리 기반 모션 프로젝션 \(\mathcal{P}_\pi\)이다. \(\mathcal{P}_\pi\)는 물리 법칙을 무시하는 denoise된 모션 $\tilde{x}^{1:H}$을 물리적으로 그럴듯한 모션
\[\begin{equation} \hat{x}^{1:H} = \mathcal{P}_\pi (\tilde{x}^{1:H}) \end{equation}\]으로 project한다. 프로젝션은 물리 시뮬레이터 안에서 캐릭터가 $\tilde{x}^{1:H}$를 모방하도록 제어하는 모션 모방 정책 $\pi$를 학습하여 얻을 수 있다. 시뮬레이터의 결과 모션 $\hat{x}^{1:H}$는 물리 법칙을 따르므로 물리적으로 그럴듯하다고 생각할 수 있다.
Motion Imitation Formulation
인간 모션 모방 task는 Markov decision process (MDP)로 공식화할 수 있다. 이 MDP는 states, actions, transition dynamics, reward function, discount factor의 튜플
\[\begin{equation} \mathcal{M} = (\mathcal{S}, \mathcal{A}, \mathcal{T}, R, \gamma) \end{equation}\]로 정의된다. 물리 시뮬레이터의 캐릭터 에이전트는 모션 모방 정책 $\pi (a^h \vert s^h)$에 따라 행동한다. State $s^h$는 캐릭터의 물리적 state (ex. joint의 각도, 속도, 위치)와 입력 모션의 다음 포즈 $\tilde{x}^{h+1}$로 구성된다. State에 $\tilde{x}^{h+1}$를 포함하여 $\pi$가 시뮬레이터에서 $\tilde{x}^{h+1}$를 모방할 수 있는 action $a^h$를 선택하도록 한다. 초기 state $s^1$에서 시작하여 에이전트는 반복적으로 $\pi$로 $a^h$를 샘플링하며, transition dynamics $\mathcal{T} (s^{h+1} \vert s^h, a^h)$가 다음 state $s^{h+1}$를 생성하고 여기서 $\hat{x}^{h+1}$를 추출할 수 있다. 정책을 $H$ step 실행하면 물리적으로 시뮬레이션된 모션 $\tilde{x}^{1:H}$를 얻을 수 있다.
Training
학습 중에는 $\hat{x}^{1:H}$가 얼마나 $\tilde{x}^{1:H}$에 잘 align되는지에 기반하여 reward $r^h$가 캐릭터에 할당된다. $\pi$는 고품질 ground-truth 모션으로 이루어진 대규모 모션 캡처 데이터셋에서 학습된다. 강화학습 (RL)을 사용하여 $\pi$를 학습시키며, 목적 함수는 discount return의 기대값
\[\begin{equation} J(\pi) = \mathbb{E}_\pi \bigg[ \sum_h \gamma^h r^h \bigg] \end{equation}\]를 최대화하여 ground-truth 모션을 가능한 가깝게 모방한다. 본 논문에서는 PPO를 사용하여 최적 정책을 찾는다.
Rewards
Reward function은 $\hat{x}^{1:H}$가 $\tilde{x}^{1:H}$에 일치하도록 만들기 위해 디자인된다. 각 timestep의 reward $r^h$는 다음과 같이 4개의 sub-reward로 구성된다.
\[\begin{aligned} r^h &= w_\textrm{p} r_\textrm{p}^h + w_\textrm{v} r_\textrm{v}^h + w_\textrm{j} r_\textrm{j}^h + w_\textrm{q} r_\textrm{q}^h \\ r_\textrm{p}^h &= \exp \bigg[ -\alpha_\textrm{p} \bigg( \sum_{j=1}^J \| o_j^h \ominus \bar{o}_j^h \|^2 \bigg) \bigg] \\ r_\textrm{v}^h &= \exp [ -\alpha_\textrm{v} \| v^h - \bar{v}^h \|^2 ] \\ r_\textrm{j}^h &= \exp \bigg[ -\alpha_\textrm{j} \bigg( \sum_{j=1}^J \| p_j^h - \bar{p}_j^h \|^2 \bigg) \bigg] \\ r_\textrm{q}^h &= \exp \bigg[ -\alpha_\textrm{q} \bigg( \sum_{j=1}^J \| q_j^h - \bar{q}_j^h \|^2 \bigg) \bigg] \end{aligned}\]여기서 $\bar{\cdot}$은 ground-truth를 나타내며, $w_\textrm{p}$, $w_\textrm{v}$, $w_\textrm{j}$, $w_\textrm{q}$, $\alpha_\textrm{p}$, $\alpha_\textrm{v}$, $\alpha_\textrm{j}$, $\alpha_\textrm{q}$는 weighting factor이다.
Pose reward $r_\textrm{p}^h$는 로컬한 joint rotation 사이의 차이를 측정한다. Velocity reward $r_\textrm{v}^h$는 joint velocity 사이의 차일를 측정한다. Joint position reward $r_\textrm{j}^h$는 3D world joint position 사이의 차이를 측정한다. Joint rotation $r_\textrm{q}^h$는 글로벌한 joint rotation 사이의 차이를 측정한다.
States
State $s^h$는 캐릭터의 현재 물리적 state와 입력 모션의 다음 포즈 $\tilde{x}^{h+1}$, 캐릭터 속성 벡터 $\psi$로 구성된다. 캐릭터의 물리적 state는 joint 각도, joint 속도, 강체(rigid body)의 위치, 회전, 선속도, 각속도를 포함한다. 입력 포즈 $\tilde{x}^{h+1}$의 경우, 강체 위치 및 회전, joint 각도에 대한 $\tilde{x}^{h+1}$의 차이를 포함한다. 차이를 사용하여 보상해야 하는 pose residual을 정책에 알려준다. 모든 feature는 캐릭터의 방향 좌표에서 계산되어 rotation과 translation의 불변성을 보장한다. 본 논문의 캐릭터가 SMPL body model을 기반으로 하므로 $\psi$는 성별과 SMPL 모양 파리미터를 포함하여 정책이 다양한 캐릭터를 제어하도록 한다.
Actions
본 논문에서는 proportional derivative (PD) controller의 joint 각도를 action 표현으로 사용하며, 이를 통해 robust한 모션 모방을 가능하게 한다. 또한 추가로 action space에 residual force를 추가하여 캐릭터를 안정화하고 어떠한 역학 불일치도 보상하도록 한다.
Policy
본 논문에서는 parameterize된 Gaussian policy $\pi (a^h \vert s^h) = \mathcal{N} (\mu_\theta (s^h), \Sigma)$를 사용하며, $\mu_\theta$는 간단한 MLP의 출력이고 $\Sigma$는 고정된 대각 분산 행렬이다. Inference 중에는 $\mu_\theta$를 직접 사용하여 noise를 제거하고 더 나은 모방 성능을 달성한다.
Experiments
본 논문의 실험은 다음 3가지 질문에 답하기 위해 디자인되었다.
- PhysDiff model이 SOTA motion diffusion model보다 더 물리적으로 그럴듯한 모션을 생성하는가?
- PhysDiff가 물리적 개연성을 개선하면서 SOTA 모션 품질을 달성할 수 있는가?
- 물리 기반 프로젝션의 다양한 schedule이 모션 생성 성능에 어떤 영향을 주는가?
실험에 대한 디테일은 다음과 같다.
- Data
- Text-to-Motion 생성: HumanML3D
- Action-to-Motion 생성: HumanAct12, UESTC
- Evaluation Metrics
- FID: 생성된 모션 분포와 ground-truth 모션 분포 사이의 거리
- R-Precision: 생성된 모션과 입력 텍스트 사이의 연관성
- Accuracy: 학습된 action classifier의 accuracy
- Penetrate: ground penetration 측정
- Float: floating 측정
- Skate: foot sliding 측정
- Phys-Err: 전체적인 물리적 오차 (Penetrate, Float, Skate의 합)
- Implementation Details
- classifier-free guidance를 사용한 50 diffusion step
- denoiser $D$로 MDM의 denoising network 사용 (공정한 비교를 위해 사전 학습된 가중치 사용)
- 물리 시뮬레이터로 IsaacGym 사용
다음은 PhysDiff model을 SOTA인 MDM과 시각적으로 비교한 것이다.
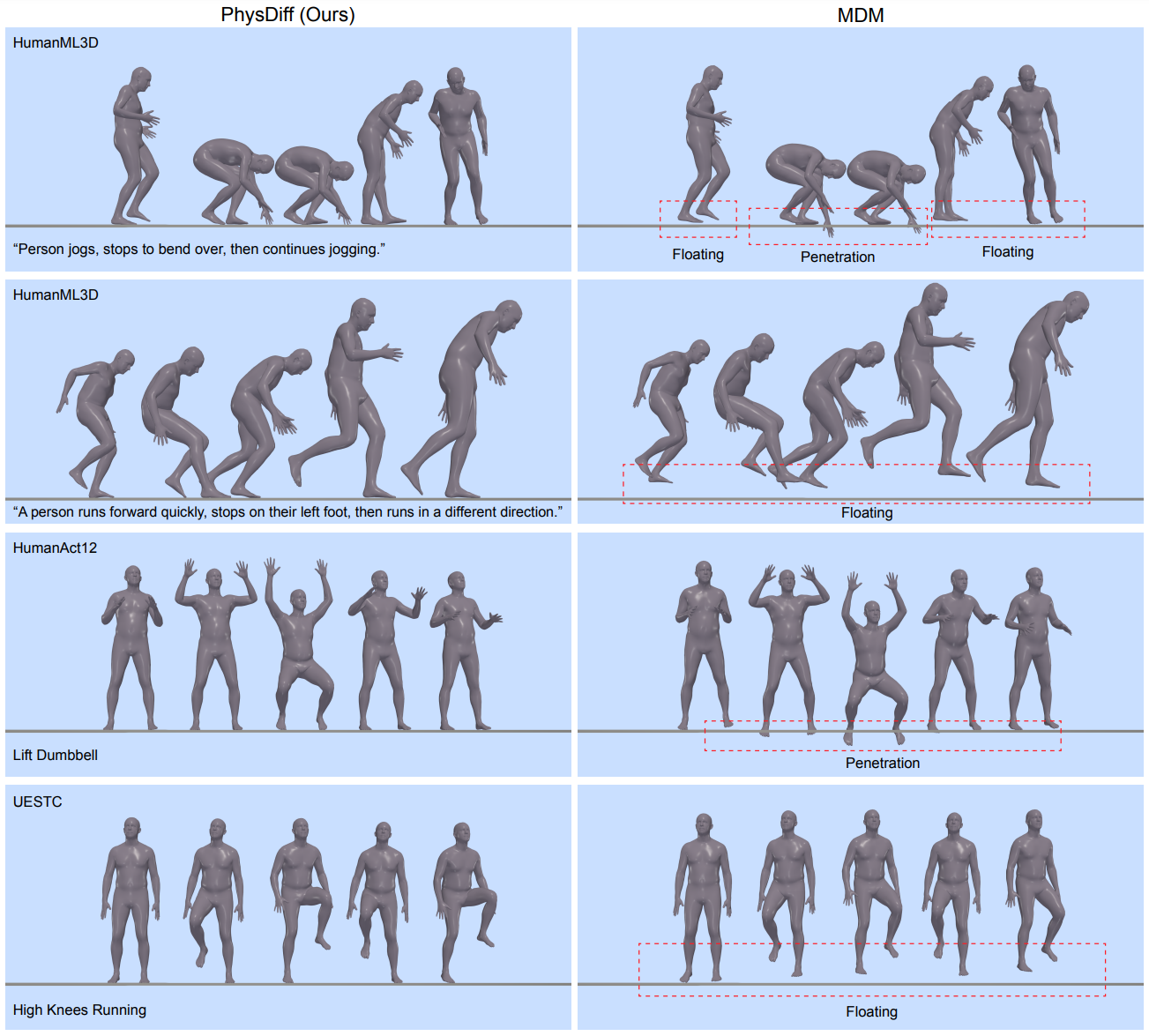
1. Text-to-Motion Generation
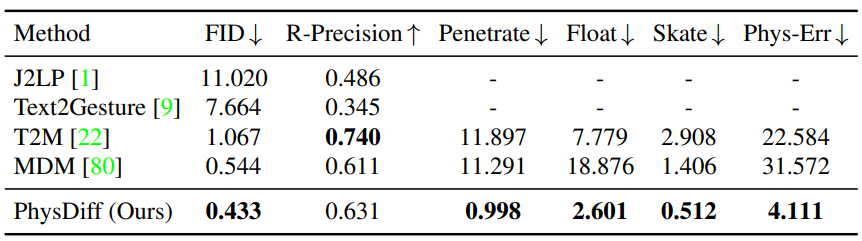
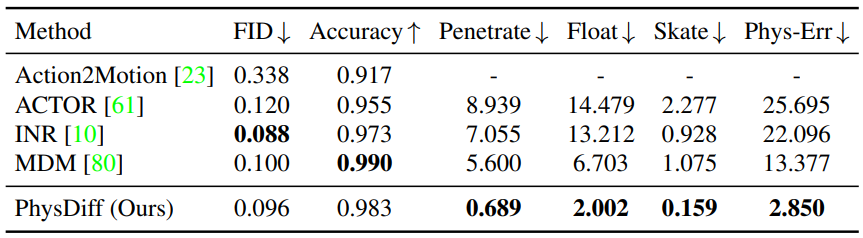
다음은 HumanML3D 데이터셋에서 PhysDiff model을 SOTA 방법들과 text-to-motion 생성에 대해 비교한 표이다.
2. Action-to-Motion Generation
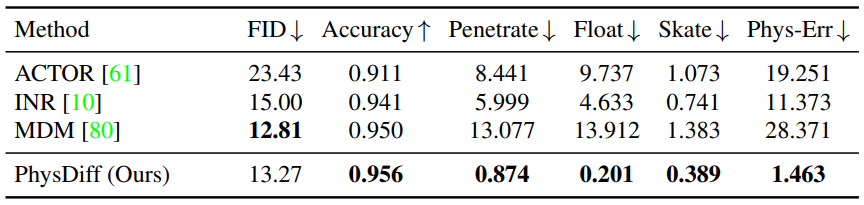
다음은 HumanAct12(위)와 UESTC(아래) 데이터셋에서 PhysDiff model을 SOTA 방법들과 action-to-motion 생성에 대해 비교한 표이다.
3. Schedule of Physics-Based Projection
저자들은 PhysDiff의 중요한 디자인 선택을 분석하기 위한 광범위한 실험을 수행하였다.
다음은 HumanML3D에서 물리 기반 프로젝션의 step 수에 따른 text-to-motion 생성의 효과를 비교한 그래프이다.
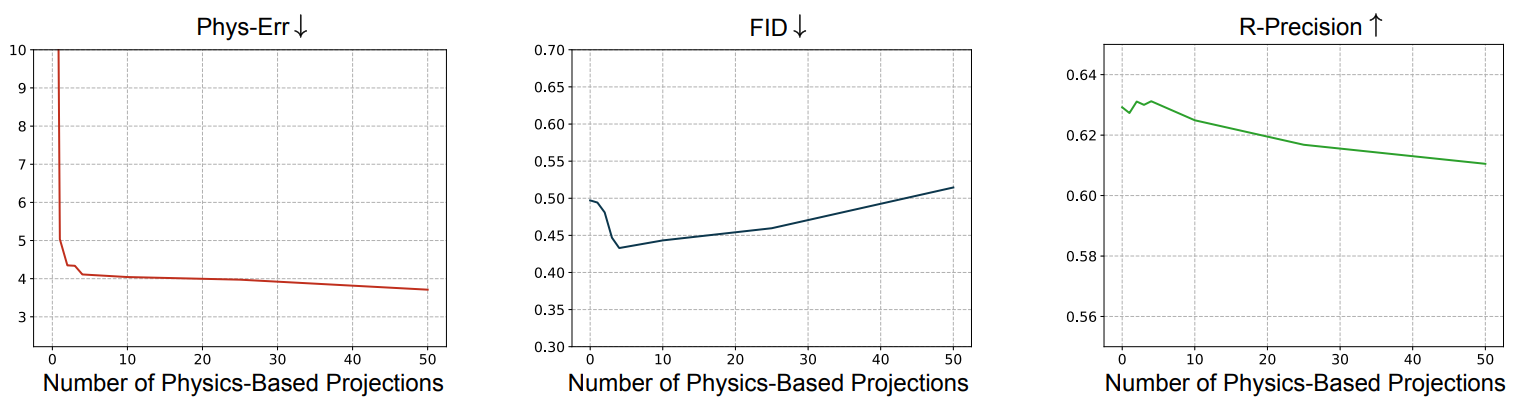
Step 수가 증가하면 Phys-Err이 감소하며, 더 많은 projection step을 사용하면 물리적 개연성이 개선돠는 데 도움이 된다. 놀라운 점은 FID와 R-Precision은 처음에 개선되다가 step 수가 증가하면 저하된다. 이는 물리적 개연성과 모션 품질 사이에 trade-off가 있음을 의미한다. 저자들은 이러한 현상이 diffusion step 초반에 생성된 모션이 물리적 개연성이 떨어지는 데이터셋의 평균 모션으로 denoise되기 때문이라는 가설을 세웠다. 결과적으로 물리 기반 프로젝션을 이른 step에 사용하면 생성된 모션이 데이터 분포 밖으로 밀어내며 diffusion process를 방해한다.
저자들은 projection step의 가장 좋은 배치를 찾기 위해 3가지 그룹의 schedule을 비교한다.
- Uniform N: $N$ projection step이 균등하게 퍼져있음
- Start M, End N: 시작 부분에 연속적인 $M$개의 projection step, 끝 부분에 $N$개의 projection step
- End N, Space S: 끝 부분에 간격 $S$로 $N$개의 projection step
다음은 HumanML3D에서 projection schedule들을 비교한 표이다.
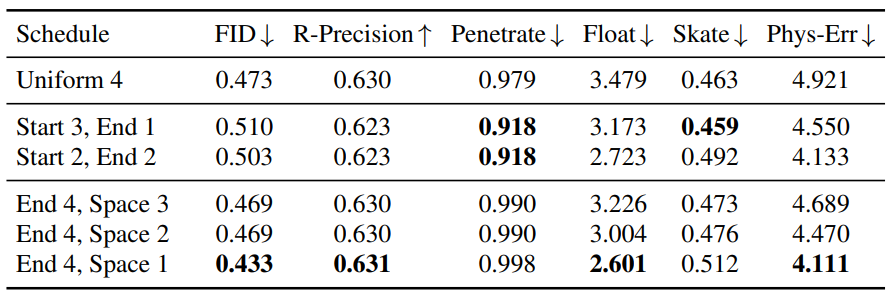
Start M, End N은 프로젝션이 이른 diffusion step에 수행되므로 샘플 품질이 좋지 못한 것으로 나타났다. Uniform N은 샘플 품질은 좋지만 Phys-Err가 나쁘다. 이는 물리 기반 프로젝션 사이의 너무 많은 비물리 기반 diffusion step이 프로젝션의 효과를 무효화하고 물리적 아티팩트를 다시 도입하기 때문일 수 있다. 이는 End 4, Space 3이 End 4, Space 1보다 성능이 좋지 못한 이유기도 하다.
Limitations
- 물리 시뮬레이션으로 인해 inference 속도가 SOTA 모델보다 2~3배 느릴 수 있다. 더 빠른 물리 시뮬레이터로 모델 속도를 높이거나 물리 기반 프로젝션을 개선하여 필요한 projection step 수를 줄일 수 있다.
- 현재 inference 중 diffusion process에만 물리가 적용된다. Diffusion model에 의해 학습된 분포를 개선하기 위해 학습 프로세스에 물리학을 추가하는 것도 흥미로울 수 있다.