[논문리뷰] Re-imagine the Negative Prompt Algorithm: Transform 2D Diffusion into 3D, alleviate Janus problem and Beyond (Perp-Neg)

arXiv 2023. [Paper] [Page] [Github]
Mohammadreza Armandpour, Ali Sadeghian, Huangjie Zheng, Amir Sadeghian, Mingyuan Zhou
Texas A&M University | Astroblox AI | The University of Texas at Austin
11 Apr 2023

Introduction

텍스트에서 diffusion model을 사용하여 이미지를 생성하는 발전은 구조화되지 않은 텍스트 입력에서 광범위한 창의적 이미지를 생성하는 놀라운 능력을 보여주었다. 그러나 연구 결과 생성된 이미지가 원래 텍스트 프롬프트의 의도된 의미를 항상 정확하게 나타내지 않을 수 있음이 밝혀졌다.

텍스트 쿼리와 semantic하게 일치하는 만족스러운 이미지를 생성하는 것은 기준 수준에서 이미지를 일치시키는 텍스트 개념이 필요하기 때문에 어렵다. 그러나 이러한 세분화된 주석을 얻기 어렵기 때문에 현재의 text-to-image 모델은 텍스트와 이미지 간의 관계를 완전히 이해하는 데 어려움이 있다. 따라서 그들은 데이터셋에서 빈도가 높은 텍스트-이미지 쌍과 같은 이미지를 생성하는 경향이 있으며 생성된 이미지가 요청되지 않았거나 원하지 않는 속성을 포함하고 있음을 관찰할 수 있다. 최근 연구들의 대부분은 잘 설계된 본문 프롬프트를 기반으로 이미지를 편집하기 위해 기존 콘텐츠에 누락된 개체 또는 속성을 다시 추가하는 데 중점을 둔다. 그러나 그들 중 일부는 중복 속성을 제거하는 방법을 연구하거나 부정 프롬프트를 사용하여 모델이 원하지 않는 개체를 가지지 않도록 하는 방법을 연구하였다.

저자들은 현재 부정 프롬프트 알고리즘의 단점을 보여줌으로써 이 논문을 시작한다. 기본 프롬프트와 부정 프롬프트가 겹치는 경우 부정 프롬프트를 사용하는 현재 구현이 만족스럽지 못한 결과를 생성할 수 있다. 위의 문제를 해결하기 위해 본 논문은 학습이 필요하지 않고 사전 학습된 diffusion model에 쉽게 적용할 수 있는 Perp-Neg 알고리즘을 제안한다. 부정 프롬프트에 대해 denoiser에 의해 추정된 수직 점수 (perpendicular score)를 사용하기 때문에 본 논문의 방법을 Perp-Neg라고 한다. 보다 구체적으로, Perp-Neg는 denoising 방향을 제한하며, 부정 프롬프트가 항상 기본 프롬프트 방향과 수직이 되도록 가이드한다. 이러한 방식으로 모델은 기본 semantic을 변경하지 않고 부정 프롬프트에서 원하지 않는 관점을 제거할 수 있다.

또한 Perp-Neg를 SOTA text-to-3D 모델인 DreamFusion으로 확장하고 Perp-Neg가 3D 생성 개체가 부정확하게 표시되는 경우를 가리키는 Janus problem을 완화할 수 있는 방법을 보여준다. 최근 연구에서는 Janus problem의 주요 원인이 사전 학습된 2D diffusion model이 프롬프트에서 제공되는 view 명령을 따르지 못하는 것으로 간주했다. 따라서 먼저 2D에서 알고리즘이 사전 학습된 diffusion model의 view 충실도를 크게 향상시킬 수 있는 방법을 정량적 및 정성적으로 보여준다. 또한 아래 그림과 같이 Perp-Neg가 3D 예시에 필요하므로 2D에서 개체의 두 view 사이에 효과적인 보간을 위해 Perp-Neg를 사용할 수 있는 방법을 살펴본다. 그런 다음 Perp-Neg를 안정적인 DreamFusion에 통합하고 이를 완화할 수 있는 방법을 보여준다.

Perp-Neg: Novel negative prompt algorithm

1. The problem of semantic overlap

모델이 복잡한 텍스트 입력을 처리하는 데 도움이 되도록 텍스트 조건을 일련의 긍정 프롬프트와 부정 프롬프트로 분해할 것을 제안하지만 제안된 방법은 이러한 조건부 프롬프트가 서로 독립적이라고 가정하므로 프롬프트를 주의 깊게 설계해야 하거나 실제로 깨닫기 너무 이상적일 수 있다. 간단하게 표현하기 위해 두 개의 프롬프트, 즉 기본 프롬프트 $c_1$과 추가 프롬프트 $c_2$를 융합한 경우의 중복 문제를 아래에 제시한다. 일반성을 잃지 않고 이 문제는 기본 프롬프트가 \(\{c_1, \ldots, c_n\}\)과 같은 일련의 프롬프트와 결합되는 경우에도 일반화될 수 있다.

\[\begin{equation} p_\theta (x, c_1, c_2) = p_\theta (x) p_\theta (c_1 \vert x) p_\theta (c_2 \vert x) \frac{p_\theta (c_1, c_2 \vert x)}{p_\theta (c_1 \vert x) p_\theta (c_2 \vert x)} \end{equation}\]

$c_1$과 $c_2$가 주어진 $x$에서 조건부 독립이면 비율

\[\begin{equation} \mathcal{R}(c_1, c_2) = \frac{p_\theta(c_1, c_2 \vert x)}{p_\theta (c_1 \vert x) p_\theta (c_2 \vert x)} = 1 \end{equation}\]

이고 이 항은 무시할 수 있다. 그러나 실제로는 스타일, 콘텐츠 및 해당 관계와 같은 이미지의 원하는 속성을 지정해야 할 때 입력 텍스트 프롬프트가 거의 독립적일 수 없다. $c_1$과 $c_2$의 의미가 겹치는 경우 개념을 단순히 융합하는 것은 해로울 수 있으며 특히 개념 부정의 경우 아래 그림과 같이 원하지 않는 결과가 발생할 수 있다.

위 이미지의 두 번째 행에서 명확하게 관찰할 수 있다. 본문 프롬프트에서 요청된 핵심 개념 (각각 “armchair”, “sunglasses”, “crown”, “horse”)은 이러한 개념이 부정 프롬프트에 나타날 때 제거된다. 이 중요한 관찰은 개념 구성 프로세스를 다시 생각하고 샘플링에서 수직 기울기의 사용을 제안하도록 동기를 부여한다.

2. Perpendicular gradient

$c_1$과 $c_2$가 독립적인 경우, 둘의 denoising score 성분은 다음과 같다.

\[\begin{equation} \epsilon_\theta^i = \epsilon_\theta (x_t, t, c_i) - \epsilon_\theta (x_t, t); \quad i = 1, 2 \end{equation}\]

이러한 denoising score를 직접 융합할 수 있다. 그러나 $c_1$과 $c_2$가 겹치는 경우 denoising 성분을 직접 융합할 수 없으므로 융합을 보장하기 위해 $c_2$의 독립 성분을 찾도록 동기를 부여한다. Denoising score는 $c_1$의 의미를 손상시키지 않는다.

$\epsilon_\theta^i$의 기하학적 해석이 생성 모델이 최종 이미지를 생성하기 위해 denoise해야 하는 기울기를 나타내는 것을 고려하면 자연스러운 해결책은 $\epsilon_\theta^1$의 수직 기울기를 $\epsilon_\theta^2$의 독립 성분으로 찾는 것이다. 따라서 $c_1$과 $c_2$에 대한 Perp-Neg 샘플러를 다음과 같이 정의한다.

\[\begin{equation} \hat{\epsilon}_\theta^\textrm{Perp} (x_t, t, c) = \epsilon_\theta (x_t, t) + w_1 \epsilon_\theta^1 + w_2 \underbrace{\bigg( \epsilon_\theta^2 - \frac{\langle \epsilon_\theta^1, \epsilon_\theta^2 \rangle}{\| \epsilon_\theta^1 \|^2} \epsilon_\theta^1 \bigg)}_{\textrm{perpendicular gradident}} \end{equation}\]

여기서 $\langle, \rangle$은 벡터 내적을 나타내고, $w_1$과 $w_2$는 각 성분에 대한 가중치이며, \(\frac{\langle \epsilon_\theta^1, \epsilon_\theta^2 \rangle}{\| \epsilon_\theta^1 \|^2}\)는 $c_2$에서 $c_1$까지의 가장 상관관계가 높은 성분을 찾기 위한 projection 함수이다.

제안된 수직 기울기 샘플러는 긍정 프롬프트와 부정 프롬프트 모두에 적용할 수 있지만 개념 결합의 경우 긍정 프롬프트는 기본 개념을 보완하는 새로운 디테일을 생성하므로 더 쉽게 기본 프롬프트와 독립적으로 설계할 수 있다. 그러나 개념 부정의 경우 부정 프롬프트가 본문 프롬프트와 겹치는 것을 관찰하는 경우가 더 많다.

수직 기울기의 가장 중요한 속성은 $\epsilon_\theta^1$의 구성 요소가 추가 프롬프트에 의해 영향을 받지 않는다는 것이다.

\[\begin{equation} \hat{\epsilon}_\theta (x_t, t, c) = \epsilon_\theta (x_t, t) + \sum_i w_i (\epsilon_\theta (x_t, t, c_i) - \epsilon_\theta (x_t, t)) \end{equation}\]

에서 $\epsilon_\theta^1 = \epsilon_\theta^2$인 경우를 상상해 보자. $w_1 = −w_2$로 설정하면 denoising 기울기가 0이 되어 생성에 실패할 수 있다. 그러나 수직 기울기를 사용하면 여전히 주성분 $\epsilon_\theta^1$를 보존할 수 있다.

3. Perp-Neg algorithm

본 논문은 부정 텍스트 프롬프트의 집합을 \(\{\tilde{c}_1, \ldots, \tilde{c}_m\}\)으로 일반화하고 Perp-Neg 알고리즘을 제시한다. $c_1$과 $\epsilon_\theta^1$을 $c_\textrm{pos}$와 \(\epsilon_\theta^\textrm{pos}\)로 표시하자. 이는 각각 주요 긍정 프롬프트 조건과 해당 denoising 성분을 나타낸다. 집합의 임의의 부정 텍스트 프롬프트 \(\tilde{c}_i\)에 대해 Perp-Neg 샘플러는 다음과 같이 정의된다.

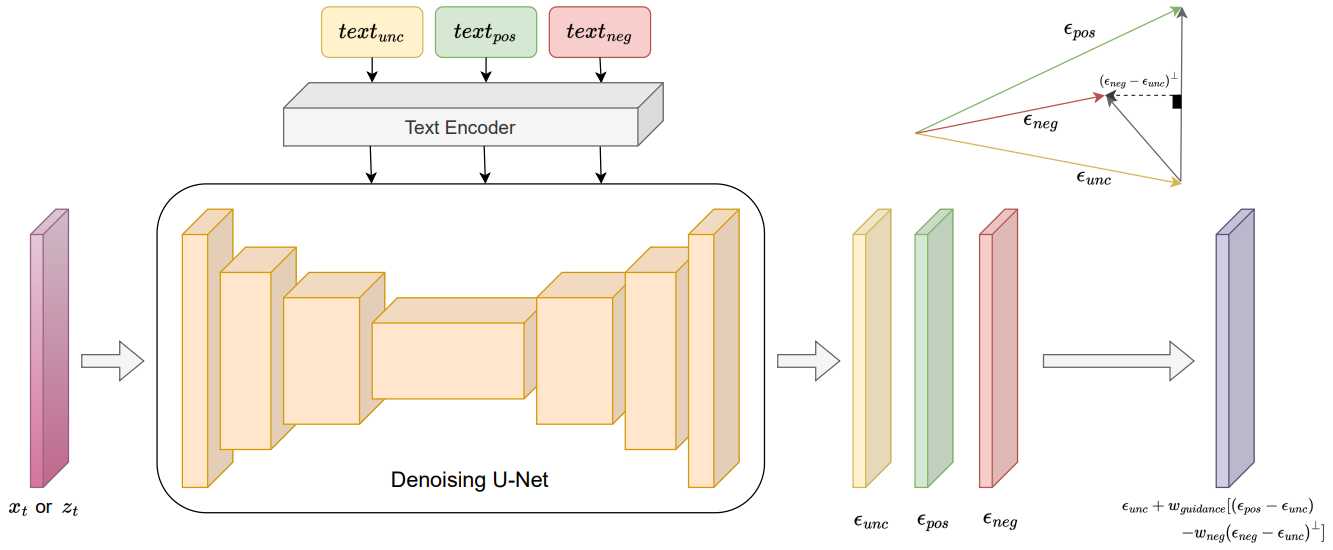
\[\begin{aligned} \epsilon_\theta^\textrm{Perp-Neg} (x_t, t, c_\textrm{pos}, \tilde{c}_i) = \;& \epsilon_\theta (x_t, t) + w_\textrm{pos} \epsilon_\theta^\textrm{pos} \\ &- \sum_i w_i \underbrace{\bigg( \epsilon_\theta^i - \frac{\langle \epsilon_\theta^\textrm{pos}, \epsilon_\theta^i \rangle}{\| \epsilon_\theta^\textrm{pos} \|^2} \epsilon_\theta^\textrm{pos} \bigg)}_{\textrm{perpendicular gradient of } \epsilon^\textrm{pos} \textrm{ on } \epsilon^i} \\ \epsilon_\theta^i = \;& \epsilon_\theta (x_t, t, \tilde{c}_i) - \epsilon_\theta (x_t, t) \end{aligned}\]

여기서 $w_\textrm{pos} > 0$와 $w_i > 0$는 긍정 프롬프트와 각 부정 프롬프트의 가중치이다. Perp-Neg 알고리즘의 개요는 아래 그림과 같다.

2D diffusion model for 3D generation

Background

2D diffusion model은 밀도 샘플을 제공할 뿐만 아니라 데이터 밀도 likelihood의 도함수를 계산할 수도 있습. 후자의 장점을 사용하여 사전 학습된 2D diffusion을 향상시키고 3D 생성 모델로 만드는 몇 가지 중요한 연구들이 있다. 이러한 모든 방법의 기본 아이디어는 diffusion model이 2D projection을 정의한 likelihood를 기반으로 객체의 3D 장면 표현 (ex. NeRF, mesh 등)을 최적화하는 것이다. 더 구체적으로 말하자면, 이러한 알고리즘은 3가지 주요 구성 요소로 구성된다.

1. 장면 $\phi$의 3D parameterization
2. $x = g(\phi, v)$가 되도록 원하는 카메라 시점 $v$에서 이미지 $x$ (또는 인코딩된 feature)를 생성하는 differentiable renderer $g$
3. $\log p(x \vert c, v)$의 프록시를 얻기 위한 사전 학습된 2D diffusion model $\theta$ ($p$는 2D 데이터 밀도, $c$는 텍스트 프롬프트)

다음과 같이 최적화 문제를 해결하여 3D 생성을 하였다.

\[\begin{equation} \phi^\ast = \underset{\phi}{\arg \min} \mathbb{E}_v [\mathcal{L} (x = g (\phi, v) \vert c, v; \theta)] \end{equation}\]

여기서 $\mathcal{L}$은 사전 학습된 diffusion model을 기반으로 하는 2D 이미지의 negative log-likelihood에 대한 프록시이다.

Noise 예측 loss는 데이터 밀도의 ELBO이기 때문에 diffusion model의 목적 함수로 $\mathcal{L}$에 대한 자연스러운 선택이다.

\[\begin{equation} \mathcal{L}_\textrm{Diff} = \mathbb{E}_{t, \epsilon} [w(t) \| \epsilon_\theta (x_t; t) - \epsilon \|_2^2] \end{equation}\]

그러나 \(\mathcal{L}_\textrm{Diff}\)의 직접 최적화는 실제 샘플을 제공하지 않는다. 따라서 Score Distillation Sampling (SDS)이 diffusion loss 기울기의 수정된 버전으로 제안되었으며, 이는 다음과 같이 보다 강력하고 계산적으로 효율적이다.

\[\begin{equation} \nabla_\phi \mathcal{L}_\textrm{SDS} (x = g(\phi)) = \mathbb{E}_{t, \epsilon} \bigg[ w(t) (\hat{\epsilon}_\theta (x_t; c, v, t) - \epsilon) \frac{\partial x}{\partial \phi} \bigg] \end{equation}\]

여기서 $\epsilon_\theta$는 \(\hat{\epsilon}_\theta\)로 대체되어 classifier-free guidance를 사용하여 텍스트 컨디셔닝을 허용한다.

직관적으로 이 loss는 timestep $t$에 해당하는 임의의 noise 양으로 $x$를 교란시키고 diffusion model의 score function을 따르는 업데이트 방향을 추정하여 고밀도 영역으로 이동한다.

1. The Janus problem

2D diffusion 기반의 3D 생성 모델이 도입된 이후 Janus (multi-faced) problem이 발생하는 것으로 알려져 있다. 이것은 학습된 3D 장면이 원하는 3D 출력을 제시하는 대신 객체의 여러 view를 서로 다른 방향으로 표시하는 현상을 나타낸다. 예를 들어, 모델이 사람/동물의 3D 샘플을 생성하도록 요청받은 경우 생성된 개체 모델에는 사람/동물의 뒷모습 대신 여러 얼굴을 가지는 현상이다.

View-dependent prompting이 해결책으로 제안되었지만 문제를 완전히 해결하지는 않는다. 그 이유 중 일부는 2D diffusion model이 프롬프트에서 제공하는 view로 완전히 컨디셔닝되지 못하기 때문이다. 예를 들어, 모델이 공작새의 뒷모습을 생성하도록 요청받았을 때 모델이 학습된 데이터에서 앞모습이 더 두드러졌기 때문에 대신 정면 모습으로 잘못 생성한다.

Janus problem의 이유 중 하나는 모델이 view $v$에서 적절하게 컨디셔닝되지 않기 때문이다. 보다 구체적으로, $\log p(x \vert c, v)$의 프록시는 $x$가 장면 설명 $y$에 대한 관점 $v$를 나타내지 않는 영역에서 밀도가 0이 되도록 완전히 제한하지 않는다. 이것이 사실이라고 생각되는 주된 이유는 밀도 샘플이 관심 방향을 반영하지 못하기 때문이다.

2. Perp-Neg to alleviate Janus problem and 2D view conditioning

\(\textrm{txt}_\textrm{back}\), \(\textrm{txt}_\textrm{side}\), \(\textrm{txt}_\textrm{front}\)를 각각 후면, 측면, 전면 view에 추가된 기본 텍스트 프롬프트로 정의하자. View를 포함하는 간단한 프롬프트를 다음과 같은 긍정 및 부정 프롬프트 집합으로 대체하여 각 view를 생성한다.

\[\begin{aligned} \textrm{txt}_\textrm{back} & \rightarrow [+ \textrm{txt}_\textrm{back}, -w_\textrm{side}^b \textrm{txt}_\textrm{side}, -w_\textrm{front}^b \textrm{txt}_\textrm{front}] \\ \textrm{txt}_\textrm{side} & \rightarrow [+ \textrm{txt}_\textrm{side}, -w_\textrm{front}^s \textrm{txt}_\textrm{front}] \\ \textrm{txt}_\textrm{front} & \rightarrow [+ \textrm{txt}_\textrm{front}, -w_\textrm{side}^f \textrm{txt}_\textrm{side}] \end{aligned}\]

여기서 $w(\cdot) \ge 0$은 부정 프롬프트의 가중치를 나타낸다. Diffusion model의 각 iteration 동안 긍정 프롬프트와 부정 프롬프트가 Perp-Neg 알고리즘에 입력된다. 대부분의 개체의 표준 view가 후면이 아니기 때문에 측면/전면 view 생성에 대한 부정적인 프롬프트로 \(\textrm{txt}_\textrm{back}\)을 포함하지 않는다. 그러나 일부 개체에 대해 후면 view가 더 두드러지는 경우 부정적인 프롬프트로 포함되어야 한다. 또한 부정적인 프롬프트의 가중치를 높이면 알고리즘이 pose factor로 작용하여 해당 view를 피하는 데 더 집중하게 된다.

측면 view와 후면 view 사이를 보간하기 위해 긍정 프롬프트로 다음 임베딩을 사용한다.

\[\begin{equation} r_\textrm{inter} \cdot \textrm{emb}_\textrm{side} + (1 - r_\textrm{inter}) \textrm{emb}_\textrm{back} \\ \textrm{where} \quad 0 \le r_\textrm{inter} \le 1 \end{equation}\]

여기서 \(\textrm{emb}_v\)는 view $v$에 대한 인코딩된 텍스트이고 $r_\textrm{inter}$는 보간 정도이다. 부정 프롬프트의 경우 다음을 사용한다.

\[\begin{equation} [-f_\textrm{sb} (r_\textrm{inter}) \textrm{txt}_\textrm{side}, -f_\textrm{fsb} (r_\textrm{inter}) \textrm{txt}_\textrm{front}] \end{equation}\]

$f_\textrm{sb}$, $f_\textrm{fsb}$는 양의 감소 함수이다. 두 번째 부정 프롬프트는 diffusion model이 전면 view에서 샘플을 생성하는 쪽으로 더 편향되어 있다는 가정을 기반으로 선택된다.

전면 view기와 측면 view 사이의 보간을 위해 긍정 프롬프트에 대한 임베딩은 다음과 같다.

\[\begin{equation} r_\textrm{inter} \cdot \textrm{emb}_\textrm{front} + (1 - r_\textrm{inter}) \textrm{emb}_\textrm{side} \end{equation}\]

부정 프롬프트의 경우 다음을 사용한다.

\[\begin{equation} [-f_\textrm{fs} (r_\textrm{inter}) \textrm{txt}_\textrm{front}, -f_\textrm{sf} (1 - r_\textrm{inter}) \textrm{txt}_\textrm{side}] \end{equation}\]

여기서 $f_\textrm{fs} (1)$, $f_\textrm{sf} (1) ≈ 0$이고 두 함수 모두 감소한다.

Perp-Neg SDS

본 논문은 Stable DreamFusion의 보간 기법을 사용했고 3D에서 2D 렌더링으로의 관련 방향에 따라 다양한 $r_\textrm{inter}$를 사용했다. 보다 구체적으로 SDS loss는 다음과 같이 수정된다.

\[\begin{aligned} \nabla_\phi \mathcal{L}_\textrm{SDS}^\textrm{PN} &= \mathbb{E}_{t, \epsilon} \bigg[ w(t) (\hat{\epsilon}_\theta^\textrm{PN} (x_t; c, v, t) - \epsilon) \frac{\partial x}{\partial \phi} \bigg] \\ \hat{\epsilon}_\theta^\textrm{PN} (x_t; c, v, t) &= e_\theta^\textrm{unc} + w_\textrm{guidance} [\epsilon_\theta^{\textrm{pos}_v} - \sum_i w_v^{(i)} \epsilon_\theta^{\textrm{neg}_v^{(i) \bot}}] \\ \epsilon_\theta^{\textrm{pos}_v} &= \epsilon_\theta (x_t, t, c_\textrm{pos}^{(v)}) - \epsilon_\theta (x_t, t) \\ \epsilon_\theta^{\textrm{neg}_v^{(i)}} &= \epsilon_\theta (x_t, t, c_{\textrm{neg}_{(i)}}^{(v)}) - \epsilon_\theta (x_t, t) \end{aligned}\]

여기서 \(c^{(v)}\)는 방향 $v$에서의 긍정 프롬프트와 부정 프롬프트의 텍스트 임베딩이다. \(\epsilon_\theta^{\textrm{neg}_v^{(i) \bot}}\)는 \(\epsilon_\theta^{\textrm{pos}_v}\)에서 \(\epsilon_\theta^{\textrm{neg}_v^{(i)}}\)의 수직 성분이다. $w_v$는 방향 $v$에서 부정 프롬프트의 가중치를 나타낸다.

Experiments

1. Statistics on semantic-aligned 2D generations

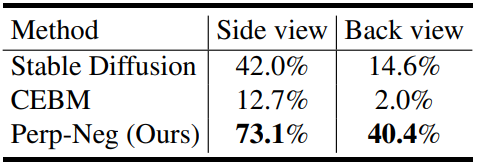
다음은 성공적인 생성 비율을 비교한 표이다.

다음은 Stable Diffusion과 함께 일반 샘플러 (왼쪽), CEBM (중간), Perp-Neg (오른쪽)을 사용하여 판다, 사자, 공작의 후면 view를 생성한 결과이다.

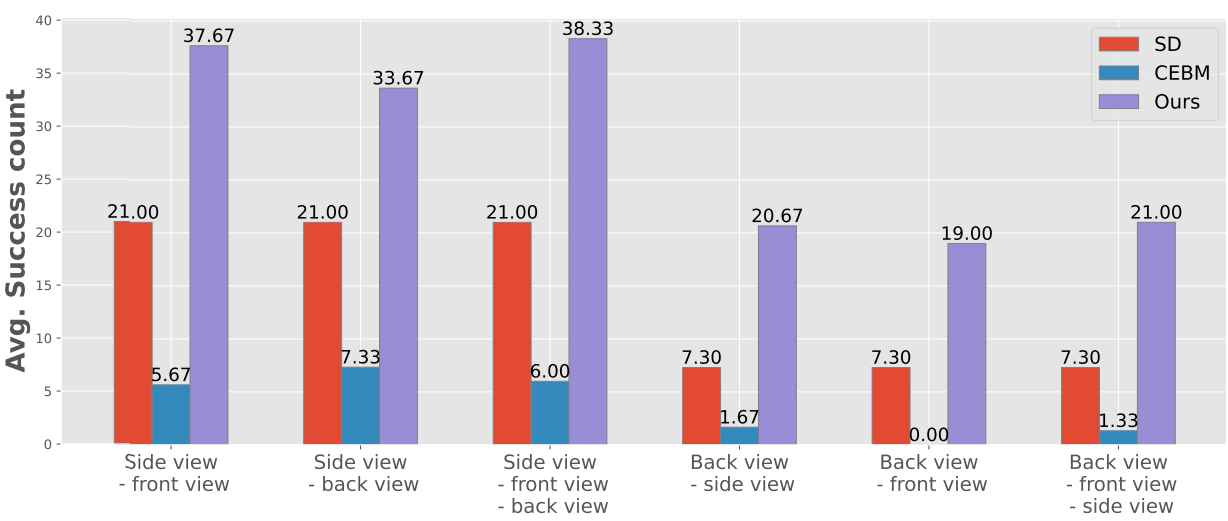
다음은 다양한 긍정 및 부정 프롬프트 조합 측면에서 성공적인 생성 수의 평균을 비교한 그래프이다.

2. Perp-Neg DreamFusion

다음은 Perp-Neg를 사용한 Stable Dreamfusion의 정성적 예시이다.