[논문리뷰] PBR-NeRF: Inverse Rendering with Physics-Based Neural Fields
CVPR 2025. [Paper] [Github]
Sean Wu, Shamik Basu, Tim Broedermann, Luc Van Gool, Christos Sakaridis
ETH Zurich | University Of Bologna | INSAIT
12 Dec 2024

Introduction
본 논문에서는 geometry, material, 조명을 공동으로 추정하여 view-dependent한 외형을 정확하게 모델링함으로써 완전한 inverse rendering 문제를 해결한다. NeILF/NeILF++ 프레임워크를 확장하여 신경망의 표현력과 PBR 이론의 이론적 보장성을 결합하였다. 특히, PBR-NeRF 방식은 NeILF/NeILF++의 기본 Disney BRDF 모델을 활용하여 반사 모델을 개선하였다. 본 방법은 에너지 보존을 강화하고 BRDF의 diffuse lobe와 specular lobe의 분리를 촉진하여 3D 재구성에서 흔히 관찰되는 diffuse albedo에 baking된 highlight와 같은 문제를 완화한다.
특히, Disney BRDF에 직접 적용된 두 가지 새로운 물리 기반 loss를 통해 이러한 목표를 달성하였다. 첫 번째 loss는 수신된 에너지보다 더 많은 에너지를 반사하는 물리적으로 유효하지 않은 BRDF에 페널티를 적용하여 에너지 보존을 강화한다. 두 번째 loss는 반사율이 높은 표면을 정확하게 모델링하는 데 필수적인 specular love와 diffuse lobe의 분리를 촉진한다. 제약 조건이 없으면, albedo를 정의하는 diffuse lobe는 거의 대칭적인 반사 각도에서 과보상하는 경향이 있으며, 두 lobe 모두 전체 BRDF에 기여한다. 목표 반사 각도에 대해 정규 분포 함수로 가중치를 적용한 diffuse lobe의 크기에 페널티를 적용함으로써, 이 loss는 specular lobe가 확장되어 specular highlight를 효과적으로 완벽하게 설명하도록 간접적으로 유도한다.
Method
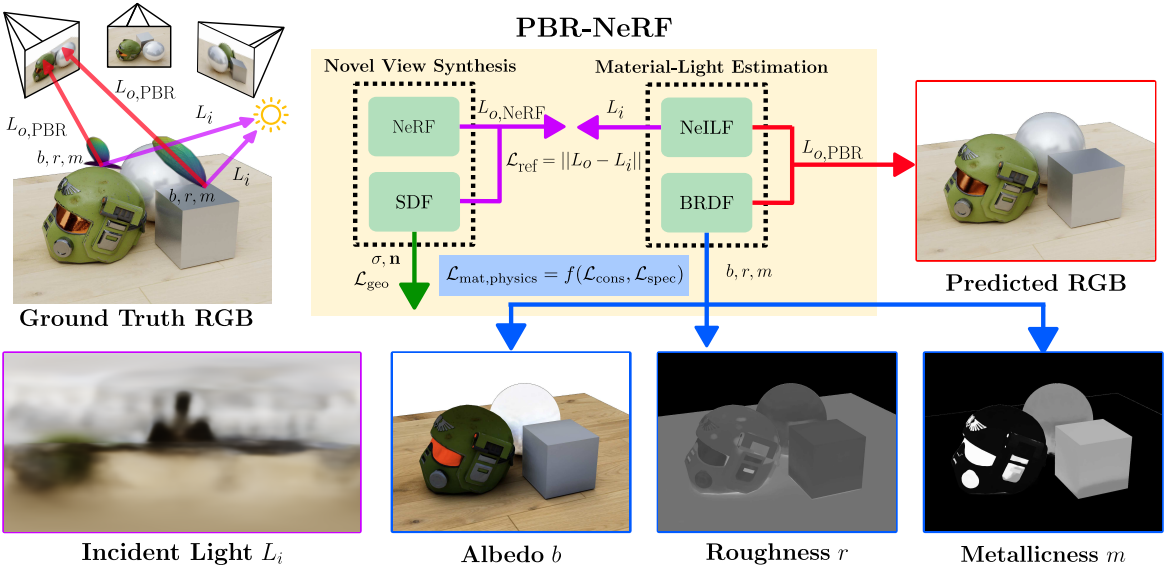
1. Background
본 논문은 NeILF++ implicit differential renderer (IDR)를 기반으로 구축되었다. IDR은 렌더링 방정식을 풀어서 출력 radiance \(L_o (\textbf{x}, \boldsymbol{\omega}_o)\)를 추정한다.
\[\begin{equation} L_o (\textbf{x}, \boldsymbol{\omega}_o) = \int_\Omega f_r (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) L_i (\textbf{x}, \boldsymbol{\omega}_i) (\boldsymbol{\omega}_i \cdot \textbf{n}) d \boldsymbol{\omega}_i \end{equation}\](\(L_o (\textbf{x}, \boldsymbol{\omega}_o)\)는 표면의 $\textbf{x}$에서 \(\boldsymbol{\omega}_o\) 방향으로 나가는 radiance, $f_r$은 BRDF, 적분은 반구 $\Omega$에서 수행)
위의 BRDF를 근사하기 위해, 공간적으로 변하는 세 가지 파라미터, 즉 albedo (base color) $b \in [0, 1]^3$, metallicness $m \in [0, 1]$, roughness $r \in [0, 1]$를 갖는 단순화된 Disney BRDF 모델을 사용한다. Disney BRDF는 diffuse lobe $f_d (\textbf{x})$와 specular lobe \(f_s (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\)로 분해된다.
\[\begin{equation} f_r (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) = f_d (\textbf{x}) + f_s (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) \end{equation}\]Diffuse lobe $f_d$는 albedo $b$와 metallicness $m$을 기반으로 view-independent한 외형을 모델링한다.
\[\begin{equation} f_d (\textbf{x}) = \frac{1 - m(\textbf{x})}{\pi} b(\textbf{x}) \end{equation}\]Specular lobe $f_s$는 ωi 방향에서 입사된 radiance $L_i$가 중간 벡터 \(\boldsymbol{\omega}_h = \frac{\boldsymbol{\omega}_o + \boldsymbol{\omega}_i}{\| \boldsymbol{\omega}_o + \boldsymbol{\omega}_i \|}\)를 가로질러 반사되어 \(\boldsymbol{\omega}_o\) 방향으로 반사되는 빛 $L_o$를 모델링한다. Disney BRDF는 microfacet BRDF 모델을 사용하여 specular lobe의 거친 표면 효과를 근사한다. Specular lobe는 다음과 같이 표현된다.
\[\begin{equation} f_s (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) = \frac{D(\boldsymbol{\omega}_h) F(\boldsymbol{\omega}_o, \boldsymbol{\omega}_h) G(\boldsymbol{\omega}_i, \boldsymbol{\omega}_o, \textbf{n})}{4 (\textbf{n} \cdot \boldsymbol{\omega}_i) (\textbf{n} \cdot \boldsymbol{\omega}_o)} \end{equation}\]여기서 normal distribution function (NDF) $D$는 microfacet 방향의 분포를 모델링하고, Fresnel 항 $F$는 Fresnel reflection을 모델링하며, $G$는 occlusion을 모델링한다. Spherical Gaussian 근사를 채택하여 roughness $r$로 NDF의 선명도를 제어한다.
\[\begin{equation} D(\boldsymbol{\omega}_h) = \frac{1}{\pi r^4} \exp \left( \frac{2}{r^4} (\boldsymbol{\omega}_h \cdot \textbf{n} - 1) \right) \end{equation}\]NeILF++를 따라 IDR 프레임워크는 세 가지 implicit network를 사용한다.
- BRDF MLP: BRDF \(f_r (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\)을 계산하기 위해 Disney BRDF 파라미터 $b$, $m$, $r$을 예측
- NeILF MLP: 들어오는 radiance \(L_i (\textbf{x}, \boldsymbol{\omega}_i)\)를 예측
- NeRF SDF: density $\sigma$와 나가는 radiance \(L_o (\textbf{x}, \boldsymbol{\omega}_o)\)를 예측
렌더링 적분을 근사하기 위해 피보나치 샘플링에 의해 생성된 고정된 \(\boldsymbol{\omega}_i\) 집합 $S_L$을 사용한다.
\[\begin{equation} L_o (\textbf{x}, \boldsymbol{\omega}_o) = \frac{2\pi}{\vert S_L \vert} \sum_{\boldsymbol{\omega}_i \in S_L} f_r (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) L_i (\textbf{x}, \boldsymbol{\omega}_i) (\boldsymbol{\omega}_i \cdot \textbf{n}) \end{equation}\]2. Physics-Based Losses
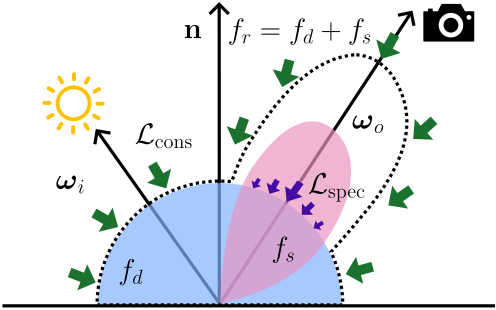
저자들은 물리적 사전 지식에서 영감을 받아 material과 조명 추정을 모두 제한하는 두 가지 새로운 loss를 제안하였다.
Conservation of Energy Loss
Disney BRDF와 기타 microfacet 모델은 에너지가 보존되지 않는 특성이 내재되어있다. 이는 inverse rendering에 심각한 문제를 야기하는데, material이 받은 빛보다 더 많은 빛을 반사하거나 (에너지 생성) 너무 적은 빛을 반사할 수 있기 때문이다 (에너지 파괴). 이러한 부정확성은 material 추정치를 왜곡하고 조명 추정을 방해하여 추정된 조명이 과도하게 보정되어 너무 밝거나 어둡게 보이게 한다.
에너지 생성 문제를 완화하기 위해, \(\int_\Omega f_r (\boldsymbol{\omega}_i \cdot \textbf{n}) d \boldsymbol{\omega}_i \ge 1\)로 설정하여 BRDF를 위한 에너지 보존 특성을 적용한다. 이 제약 조건은 반구 $\Omega$의 모든 입사 방향에 대한 반사 radiance 가중치의 합이 1을 초과해서는 안 된다는 것을 요구한다. 이러한 고유한 물리적 특성을 입사광과 무관하게 적용함으로써, 물리적으로 정확한 material을 확보할 수 있다.
이 제약 조건을 discretize된 설정에서 재구성한 Conservation of Energy Loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{cons} = \max \left\{ \left( \frac{2\pi}{\vert S_L \vert} \sum_{\boldsymbol{\omega}_i \in S_L} f_r (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) (\boldsymbol{\omega}_i \cdot \textbf{n}) \right) - 1.0 \right\} \end{equation}\]이 ReLU 스타일 공식은 반사된 irradiance가 입사된 irradiance를 초과하지 않고 변하도록 한다. \(f_r (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) (\boldsymbol{\omega}_i \cdot \textbf{n})\)의 가중 합이 1을 초과할 때만 모델에 페널티를 부여하지만, 그보다 작은 값은 자유롭게 변할 수 있다. \(\mathcal{L}_\textrm{cons}\)는 specular lobe와 diffuse lobe 모두에 영향을 미쳐 전체 BRDF $f_r$이 에너지를 보존하도록 한다.
NDF-weighted Specular Loss
두 번째 물리 기반 loss는 NeILF++와 같이 Lambertian reflection을 가정하는 inverse rendering 방식에서 자주 관찰되는 diffuse lobe와 specular lobe 사이의 불균형을 해결하는 데 중점을 둔다. 그러나 실제 material은 이상적인 램버시안 거동을 위반하는 경우가 많아, 예측된 diffuse lobe $f_d$가 불충분한 정반사를 과도하게 보상하는 baking된 specular highlight가 발생한다. 이러한 baking된 specular highlight의 경우, 총 BRDF 값 $f_r$은 specular 방향에 대해서는 정확할 수 있지만, $f_d$와 $f_s$ 사이의 불균형으로 인해 정반사가 아닌 각도에서는 diffuse 성분이 부정확해져 material 추정 품질이 저하된다.
이 불균형을 수정하기 위해 specular 영역에서 과도한 난반사(diffuse reflection)에 페널티를 주기 위해 NDF-weighted Specular Loss를 다음과 같이 정의한다.
\[\begin{equation} \mathcal{L}_\textrm{spec} = \frac{1}{\vert S_L \vert} \sum_{\boldsymbol{\omega}_i \in S_L} \textrm{softmax} \left( \frac{\textrm{detach} (D (\boldsymbol{\omega}_h))}{T_\textrm{spec}} \right) f_d \end{equation}\](\(T_\textrm{spec}\)은 temperature)
Softmax를 적용한 NDF를 사용하여, 정반사 효과가 지배적인 영역에서 난반사에 선택적으로 페널티를 부여한다. Backpropagation 과정에서 \(D(\boldsymbol{\omega}_h)\)를 통한 gradient flow를 방지하기 위해 계산 그래프에서 NDF 항을 분리하여 \(\mathcal{L}_\textrm{spec}\)에 대한 diffuse 기여도만 가중치 업데이트를 수행하도록 한다.
NDF-weighted Specular Loss는 페널티를 받은 diffuse lobe $f_d$에 specular lobe $f_s$를 증가시켜 난반사와 정반사 사이의 분리를 더욱 강화한다. RGB 렌더링 loss와 기타 정규화 항의 적절한 가중치를 적용하면 diffuse lobe가 \(\mathcal{L}_\textrm{spec}\)에 의해 임의로 억제되지 않는다. \(\mathcal{L}_\textrm{cons}\)와 마찬가지로, \(\mathcal{L}_\textrm{spec}\)은 조명 추정에도 도움이 된다. Diffuse lobe가 너무 크면 빛의 세기가 과소평가될 수 있으며, 과도한 난반사는 추정된 입사광이 시점에 따라 달라지는 정반사 효과를 잘못 재현하게 만들 수도 있다. 두 loss를 함께 적용하면 material과 조명 추정의 정확도가 크게 향상되어 장면 재구성이 더욱 현실적으로 이루어진다.
3. Joint Optimization
NeILF++를 따라 장면 재구성을 세 단계로 최적화한다.
- Geometry: Geometry를 초기화하기 위해 geometry 기반 loss \(\mathcal{L}_\textrm{geo}\)를 사용하여 NeRF SDF만 학습시킨다.
- Material: Material과 조명을 초기화하기 위해 NeRF SDF를 고정시키고 material 기반 loss \(\mathcal{L}_\textrm{mat}\)으로 NeILF MLP와 BRDF MLP를 학습시킨다.
- 공동 최적화: 모든 MLP를 \(\mathcal{L} = \mathcal{L}_\textrm{geo} + \mathcal{L}_\textrm{mat}\)으로 공동으로 학습시킨다.
각 단계는 해당 단계와 관련된 서로 다른 loss를 사용한다. 완전한 물리 기반 loss \(\mathcal{L}_\textrm{mat,physics}\)를 포함한 전체 material 기반 loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{mat} = \lambda_\textrm{pbr} \mathcal{L}_\textrm{pbr} + \lambda_\textrm{ref} \mathcal{L}_\textrm{ref} + \lambda_\textrm{smth} \mathcal{L}_\textrm{smth} + \mathcal{L}_\textrm{mat,physics} \\ \textrm{where} \quad \mathcal{L}_\textrm{mat,physics} = \lambda_\textrm{cons} \mathcal{L}_\textrm{cons} + \lambda_\textrm{spec} \mathcal{L}_\textrm{spec} \end{equation}\](\(\mathcal{L}_\textrm{pbr}\)은 표준 RGB 렌더링 loss, \(\mathcal{L}_\textrm{ref}\)는 NeILF++ reflection loss, \(\mathcal{L}_\textrm{smth}\)는 NeILF/NeILF++ BRDF smoothness loss)
Experiments
- 데이터셋: NeILF++, DTU
- 구현 디테일
- $\vert S_L \vert = 256$
- batch size: 8,192
- 각 학습 단계는 5K, 1K, 30K iteration
- learning rate: 0.002
- 공동 최적화 단계에서는 10K 마다 1/5
- GPU: NVIDIA A6000 1개로 3~7.5시간 소요
- 가중치
- NeILF++ 데이터셋: \(\lambda_\textrm{cons} = 0.01\), \(\lambda_\textrm{spec} = 0.5\)
- DTU 데이터셋: \(\lambda_\textrm{cons} = 0.01\), \(\lambda_\textrm{spec} = 0.01\)
- 나머지 hyperparameter는 NeILF++와 동일
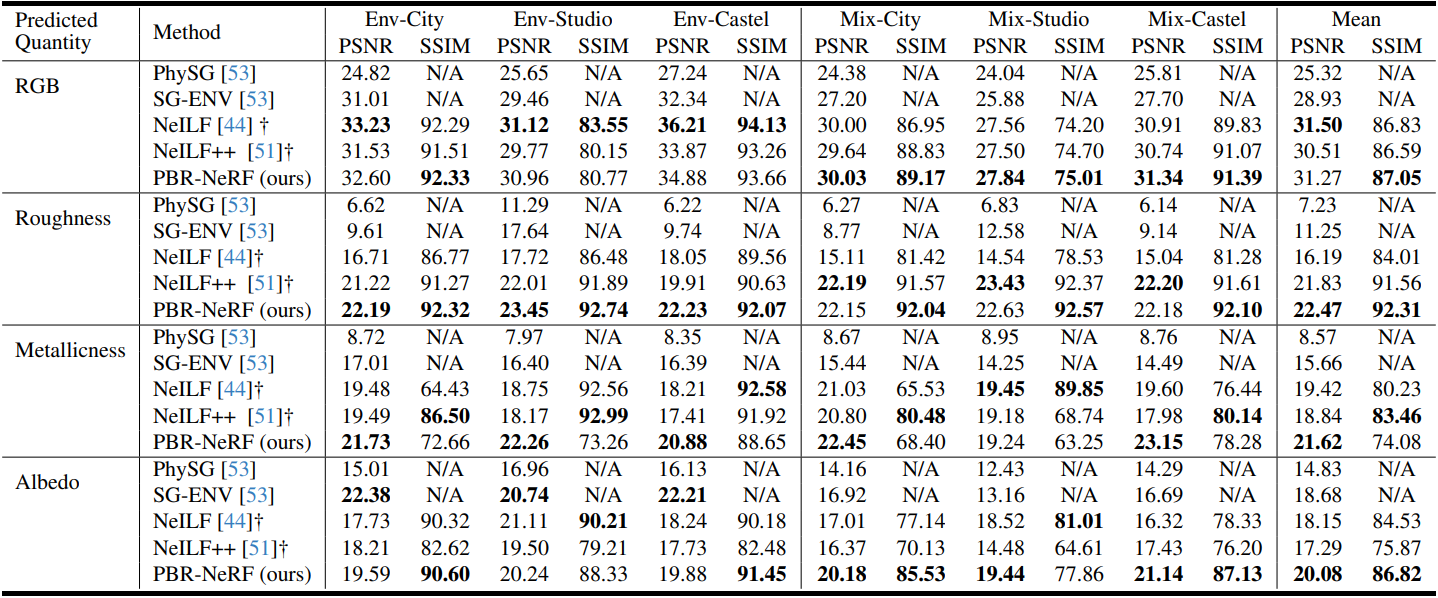
1. Comparison with The State of The Art
다음은 NeILF++ 데이터셋에서의 비교 결과이다.

다음은 DTU 데이터셋에서의 비교 결과이다.


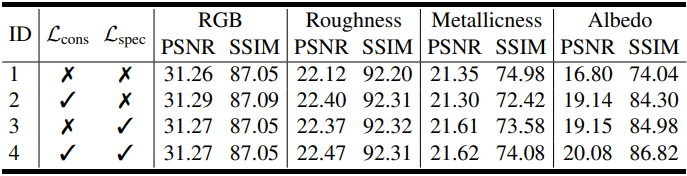
2. Ablation Study
다음은 ablation study 결과이다.