[논문리뷰] Patch Diffusion: Faster and More Data-Efficient Training of Diffusion Models

arXiv 2023. [Paper] [Github]
Zhendong Wang, Yifan Jiang, Huangjie Zheng, Peihao Wang, Pengcheng He, Zhangyang Wang, Weizhu Chen, Mingyuan Zhou
The University of Texas at Austin | Microsoft Azure AI
26 Apr 2023

Introduction

Diffusion model은 비용이 많이 들고 학습에 많은 데이터가 필요하다. 고차원의 복잡한 데이터 분포를 캡처하려면 대규모 데이터셋과 많은 iteration이 필요하다. 예를 들어, DDPM은 각각 64$\times$64 및 256$\times$256 해상도 데이터셋에 대해 8개의 V100 GPU에서 학습하는 데 약 4일과 2주 이상이 걸린다. 최신 diffusion model은 고품질 샘플을 생성하는 데 150~1000 V100 GPU day가 필요하다. 데이터의 해상도와 다양성이 증가함에 따라 학습 비용은 기하급수적으로 증가한다. 또한 가장 성능이 좋은 모델인 Imagen과 Stable Diffusion은 OpenImages와 LAION과 같은 수십억 개의 이미지를 포함한 이미지 데이터셋에 의존하며, 쉽게 액세스하거나 확장할 수 없다.

엄청난 계산 능력과 데이터를 사용하여 diffusion model을 학습하면 거의 틀림없이 놀라운 결과를 얻을 수 있지만 diffusion model을 학습하는 데 필요한 막대한 시간과 데이터 규모는 생성 AI를 민주화하는 데 중요한 한계점이다. Diffusion model 학습을 민주화하기 위해 본 논문은 UNet 아키텍처, 샘플러, noise schedule의 모든 선택에 구애받지 않는 plug-and-play 학습 테크닉인 patch-wise diffusion training (Patch Diffusion)을 제안하였다. 각 픽셀에 대한 전체 크기 이미지에서 score function을 학습하는 대신 원본 이미지의 패치 위치와 패치 크기가 모두 조건인 이미지 패치에 대한 조건부 score function을 학습할 것을 제안하였다. 전체 이미지 대신 패치로 학습하면 iteration당 계산 부담이 크게 줄어든다. 패치 위치의 조건을 통합하기 위해 픽셀 수준의 좌표계를 구성하고 diffusion model의 입력으로 원본 이미지 채널과 concat되는 추가 좌표 채널로 패치 위치 정보를 인코딩한다. 또한 여러 스케일에서 cross-region dependency를 캡처하기 위해 학습 전반에 걸쳐 점진적 또는 확률적 schedule로 패치 크기를 다양화할 것을 제안하였다.

Patch Diffusion은 diffusion model의 데이터 효율성을 개선하면서 학습 시간 비용을 크게 줄이는 것을 목표로 한다. 본 논문의 방법을 사용한 샘플링은 원래 diffusion model에서처럼 쉽다. 원본 이미지에 대한 전체 좌표를 계산하고 parameterize하고, 이를 샘플링된 noise와 concat한 다음 diffusion chain을 반전시켜 샘플을 수집한다. Patch Diffusion을 통해 유사하거나 더 나은 생성 품질을 유지하면서 2배보다 더 빠른 학습을 달성할 수 있다. 또한 Patch Diffusion은 상대적으로 작은 데이터셋에서 학습된 diffusion model의 성능을 향상시킨다.

Patch Diffusion Training

각 데이터 포인트가 데이터 분포 $p(x)$에서 독립적으로 뽑힌 데이터셋 \(\{x_n\}_{n=1}^N\)이 있다고 가정한다. 데이터에 표준 편차 $\sigma$를 갖는 독립적이고 동일하게 분포된 Gaussian noise를 추가하여 얻은 $p_\sigma (\tilde{x} \vert x) = \mathcal{N}(\tilde{x}; x, \sigma I)$를 고려한다. 양의 noise scale 시퀀스

\[\begin{equation} \sigma_\textrm{min} = \sigma_0 < \cdots < \sigma_t < \cdots < \sigma_T = \sigma_\textrm{max} \end{equation}\]

에 대하여 forward diffusion process $p_{\sigma_t} (x)$는 \(p_{\sigma_\textrm{min}} (x) \approx p(x)\)가 되도록 \(\sigma_\textrm{min}\)이 충분히 작고 \(p_{\sigma_\textrm{max}} \approx \mathcal{N}(0, \sigma_\textrm{max}^2 I)\)이 되도록 \(\sigma_\textrm{max}\)가 충분히 크다고 정의된다. Diffusion model의 목표는 chain을 reverse시키고 데이터 분포 $p(x)$를 복원하는 방법을 배우는 것이다.

무한한 수의 noise schedule $T \rightarrow \infty$로 일반화하면 forward diffusion process는 확률적 미분 방정식(SDE)으로 나타낼 수 있으며 추가로 상미분 방정식(ODE)으로 변환될 수 있다. Reverse SDE의 closed form은 다음과 같다.

\[\begin{equation} dx = [f(x, t) - g^2 (t) \nabla_x \log p_{\sigma_t} (x)] dw \end{equation}\]

여기서 $f(\cdot, t) : \mathbb{R}^d \rightarrow \mathbb{R}^d$는 drift coefficient라고 하는 벡터 값 함수, $g(t) \in \mathbb{R}$은 diffusion coefficient라고 하는 실수 값 함수, $dt$는 음의 무한소 시간 간격, $w$는 standard Brownian motion을 나타내며 $dw$는 infinitesimal white noise로 볼 수 있다. Reverse SDE의 해당 ODE는 다음과 같이 probability flow ODE라 하며, 다음과 같다.

\[\begin{equation} dx = [f(x, t) - 0.5 g^2 (t) \nabla_x \log p_{\sigma_t} (x)] dt \end{equation}\]

Reverse SDE 또는 ODE를 풀려면 $p_{\sigma_T}(x)$와 score function $\nabla_x \log p_{\sigma_t} (x)$를 모두 알아야 한다. $\nabla_x \log p_{\sigma_t} (x)$는 일반적으로 다루기 어렵기 때문에 신경망에 의해 모델링되는 함수 $s_\theta (x, \sigma_t)$를 학습하여 그 값을 추정한다. Denoising score matching은 현재 diffusion model에 적용되는 score function을 추정하는 가장 인기 있는 방법이다. 추정된 score function $s_\theta (x_, \sigma_t)$를 학습한 후 추정된 데이터 분포에서 데이터 샘플을 수집하기 위해 추정된 reverse SDE 또는 ODE를 얻을 수 있다.

1. Patch-wise Score Matching

Elucidating the design space of diffusion-based generative models 논문의 denoising score matching을 따라, 다음과 같이 표현되는 임의의 $\sigma_t$에 대해 독립적으로 데이터 분포 $p(x)$에서 추출한 샘플에 대해 예상되는 $L_2$ denoising 오차를 최소화하는 denoising function $D_\theta (x; \sigma_t)$를 구축한다.

\[\begin{equation} \mathbb{E}_{x \sim p(x)} \mathbb{E}_{\epsilon \sim \mathcal{N}(0,\sigma_t^2 I)} \| D_\theta (x+\epsilon; \sigma_t) - x \|_2^2 \end{equation}\]

따라서 다음과 같은 score function을 얻을 수 있다.

\[\begin{equation} s_\theta (x, \sigma_t) = (D_\theta (x; \sigma_t) - x) / \sigma_t^2 \end{equation}\]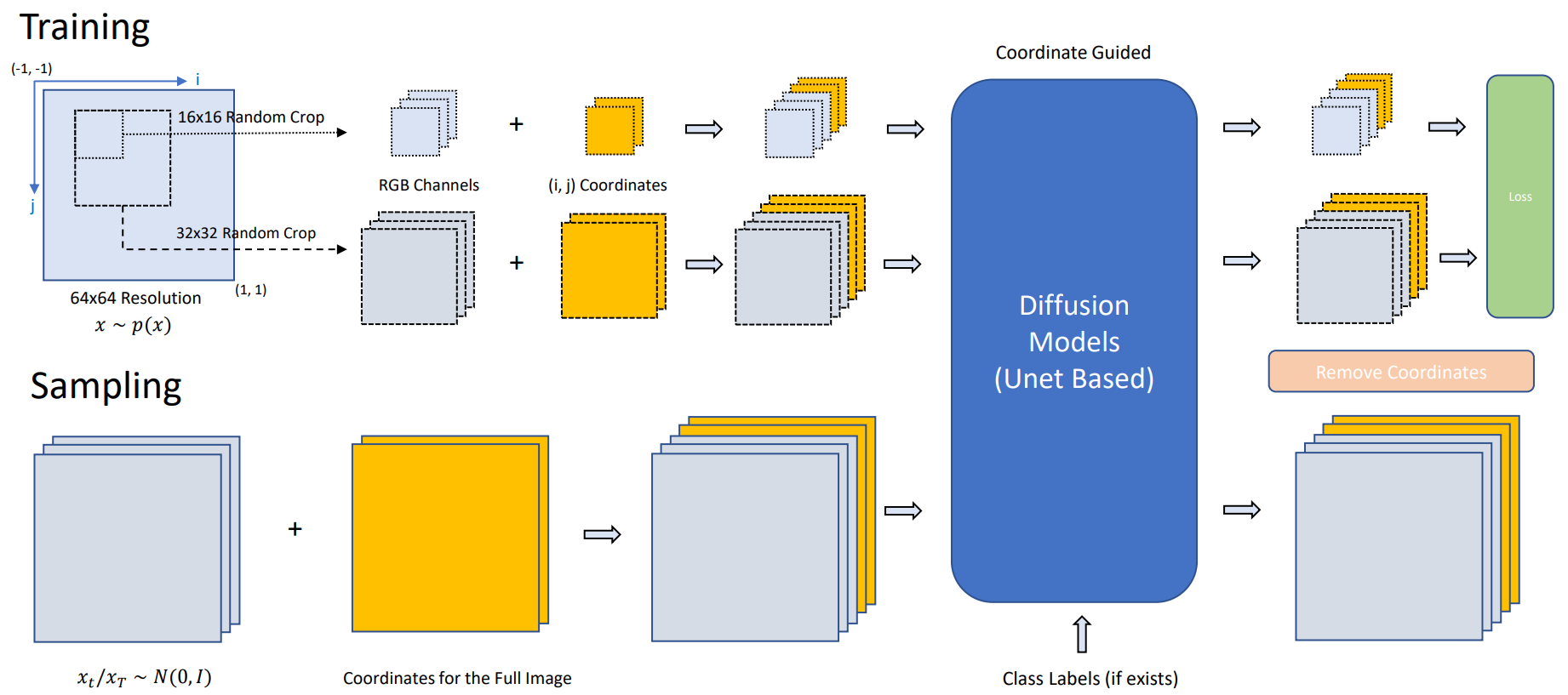

본 논문은 전체 이미지에 대해 score matching을 수행하는 대신 임의의 크기의 패치에서 score function을 학습할 것을 제안한다. 위 그림에서 볼 수 있듯이 임의의 $x \sim p(x)$에 대해 먼저 작은 패치 $x_{i,j,s}$를 랜덤하게 잘라낸다. 여기서 왼쪽 위 모서리 픽셀 좌표인 $(i,j)$를 사용하여 각 이미지 패치를 찾는다. $s$는 패치 크기를 나타낸다. 해당 패치 위치 및 크기를 조건으로 하여 이미지 패치에서 denoising score matching을 수행하며 다음과 같이 표현된다.

\[\begin{equation} \mathbb{E}_{x \sim p(x), \epsilon \sim \mathcal{N}(0, \sigma_t^2 I), (i, j, s) \sim \mathcal{U}} \| D_\theta (\tilde{x}_{i, j, s}; \sigma_t, i, j, s) - x_{i,j,s} \|_2^2 \end{equation}\]

여기서 \(\tilde{x}_{i,j,s} = x_{i,j,s} + \epsilon\)이고 $i$, $j$, $s$는 $\mathcal{U}([-1, 1])$에서 뽑는다. 그런 다음 방정식 조건부 score function $s_\theta (x, \sigma_t, i, j, s)$가 각 로컬 패치에 정의된다. 위치 및 패치 크기에 따라 각 이미지 패치 조건 내의 픽셀에 대한 score를 학습한다.

위 식을 적용하면 $D_\theta$에 작은 로컬 패치만 공급되는 경우 학습 속도가 크게 향상되고 GPU 메모리 요구 사항도 크게 감소한다.

그러나 이제 문제는 score function $s_θ(x, \sigma_t, i, j, s)$가 로컬 패치만 보았고 로컬 패치 간의 글로벌한 cross-region dependency, 즉 학습된 score를 캡처하지 않았을 수 있다는 점에 있다. 주변 패치에서 일관된 이미지 샘플링을 유도하기 위해 일관된 score map을 형성해야 한다. 저자들은 이 문제를 해결하기 위해 두 가지 전략을 제안한다.

1. 랜덤 패치 크기
2. 전체 크기 이미지의 작은 비율을 포함

학습 패치 크기는 작은 패치 크기와 큰 패치 크기의 혼합에서 샘플링되며 crop된 큰 패치는 일련의 작은 패치로 볼 수 있다. 이러한 방식으로 score function $s_\theta$는 작은 패치의 score를 통합하여 큰 패치에서 학습할 때 일관된 score map을 형성하는 방법을 학습한다. 원래 데이터 분포에 대한 reverse diffusion의 수렴을 보장하기 위해 학습 중 작은 비율의 iteration에서 전체 크기 이미지를 볼 수 있어야 한다.

2. Progressive and Stochastic Patch Size Scheduling

Cross-region dependency에서 score function에 대한 인식을 강화하기 위해 patch-size scheduling을 사용한다. 전체 크기 이미지를 $p$로, 원본 이미지 해상도를 $R$로 입력으로 취하는 iteration 비율을 나타낸다.

\[\begin{equation} s \sim p_s := \begin{cases} p & \quad \textrm{when} s = R, \\ \frac{3}{5} (1-p) & \quad \textrm{when} s = R//2 \\ \frac{2}{5} (1-p) & \quad \textrm{when} s = R//4 \end{cases} \end{equation}\]

두 가지 patch-size scheduling을 고려할 수 있다.

1. Stochastic: 학습하는 동안 위에 정의된 확률 질량 함수를 사용하여 각 mini-batch에 대해 랜덤하게 $s \sim p_s$를 샘플링한다.
2. Progressive: 작은 패치에서 큰 패치로 조건부 score function을 학습한다. 처음 $\frac{2}{5} (1 - p)$ iteration에서는 패치 크기를 $s = R//$4로 고정하고 두 번째 $\frac{3}{5} (1 - p)$ iteration에서는 $s = R//2$를 적용한다. 마지막으로 전체 반복의 $p$ 비율에 대해 전체 크기 이미지에서 모델을 학습한다.

경험적으로 $p = 0.5$ stochastic scheduling이 학습 효율성과 생성 품질 사이의 trade-off에서 좋은 결과에 도달한다고 한다.

UNet 아키텍처는 convolutional layer로 완전히 설계되었으며 convolutional filter가 입력 주위를 이동하여 모든 해상도 이미지를 처리할 수 있다. 따라서 patch diffusion 학습은 모든 UNet 기반 diffusion model에 대한 plug-and-play 학습 테크닉으로 간주될 수 있다. 또한 이미지 해상도에 대한 UNet의 유연성은 샘플링을 쉽고 빠르게 만든다.

3. Conditional Coordinates for Patch Location

Score function에서 패치 위치의 조건을 추가로 통합하고 단순화하기 위해 픽셀 수준 좌표계를 구축한다. 이미지의 왼쪽 위 모서리를 $(-1, -1)$로 설정하고 오른쪽 아래 모서리를 $(1, 1)$로 설정하여 원본 이미지 해상도에 대해 픽셀 좌표 값을 정규화한다.

이미지 패치 $x_{i,j,s}$에 대해 $i$ 및 $j$ 픽셀 좌표를 두 개의 추가 채널로 추출한다. 각 학습 batch에 대한 샘플링된 패치 크기로 각 데이터 샘플을 독립적으로 랜덤하게 crop하고 해당 좌표 채널을 추출한다. 두 개의 좌표 채널을 원본 이미지 채널과 concat하여 $D_\theta$의 입력을 구성한다. Loss를 계산할 때 재구성된 좌표 채널을 버리고 이미지 채널의 loss만 최소화한다.

임의의 패치 크기와 함께 픽셀 수준의 좌표계는 일종의 data augmentation 방법으로 볼 수 있다. 예를 들어 해상도가 64$\times$64이고 패치 크기가 $s = 16$인 이미지의 경우 $(64 − 16 + 1)^2 = 2401$개의 다른 위치가 지정된 패치를 가질 수 있다. 따라서 저자들은 diffusion model을 패치 방식으로 학습하면 diffusion model의 데이터 효율성에 도움이 될 것이라고 생각하였다. 즉, patch diffusion을 사용하면 diffusion model이 작은 데이터셋에서 더 잘 수행될 수 있다.

4. Sampling

좌표계와 UNet의 도움으로 reverse sampling을 쉽게 할 수 있다. 전체 이미지의 좌표를 계산 및 parameterize하고 각 reverse iteration에서 좌표 조건으로 마지막 step의 이미지 샘플과 함께 concat한다. 각 reverse iteration에서 좌표 채널의 재구성 출력을 버린다.

5. Theoretical Interpretations

두 가지 관점에서 patch diffusion에 대한 수학적 직관을 설명할 수 있다.

Markov Random Field

Markov Random Field(MRF)는 모델링 종속성의 압축성과 표현력으로 인해 이미지 분포를 나타내는 데 널리 사용되었다. 일반적으로 이미지는 MRF에서 방향이 없는 일반 그래프(픽셀 그리드) $\mathcal{G} = (\mathcal{V}, \mathcal{E})$로 모델링되며 각 픽셀은 그래프 정점으로 간주되며 각 정점은 이미지의 인접 픽셀에 연결된다. 따라서 이미지에 대해 정의된 PDF를 나타내기 위해 clique factorization 형식을 채택할 수 있다.

\[\begin{equation} p(x) = \frac{1}{Z} \prod_{v \in \mathcal{V}} \phi_v (x_v) \prod_{e \in \mathcal{E}} \phi_e (x_e) \end{equation}\]

여기서 $\phi_v$와 $\phi_e$는 각각 node potential function와 edge potential function이다. $Z$는 정규화 항이고 $x_v$와 $x_e$는 첨자 $v$와 $e$로 확률 변수를 인덱싱한다.

MRF parameterization의 score function은 다음과 같이 나타낼 수 있다.

\[\begin{equation} \nabla \log p (x) = \sum_{v \in \mathcal{V}} \nabla \log \phi_v (x_v) + \sum_{e \in \mathcal{E}} \nabla \log \phi_e (x_e) \end{equation}\]

여기서 $Z$는 $x$와 관련이 없으므로 제거된다. Score function은 결국 독립적인 조각으로 분해될 수 있다. 즉, 먼저 각 score function $\nabla \log \phi_v$와 $\nabla \log \phi_e$를 개별적으로 학습한 다음 inference 중에 전체 score function을 근사화하기 위해 평균을 낼 수 있다.

학습 절차는 다음과 같이 볼 수 있다. $\mathcal{V}$와 $\mathcal{E}$의 하위 집합을 포함하는 패치를 샘플링할 때마다 해당 $\nabla \log \phi_v$와 $\nabla \log \phi_e$에 대해 score matching을 수행한다. $\nabla \log \phi_v$와 $\nabla \log \phi_e$에 대한 위치 종속성을 모델링하기 위해 좌표로 네트워크를 컨디셔닝한다.

Linear Regression

최소 제곱의 관점으로 patch-wise score matching을 해설할 수도 있다. 데모 예제로 다변량 가우시안 분포를 생각해보자. 목표 분포를 $p_\mu (x) = \mathcal{N}(x \vert \mu, \Sigma)$로 parameterize한다고 가정하자. 여기서 $\mu$는 optimizer이다. 그런 다음 score function은 다음과 같이 쓸 수 있다.

\[\begin{equation} \nabla \log p_{\mu, \Sigma} (x) = −\Sigma(x − \mu). \end{equation}\]

전체 크기 이미지와 일치하는 원래 score는 다음의 최소 제곱 문제와 동일하다.

\[\begin{equation} \mathbb{E}_{x \sim p(x)} \mathbb{E}_{\epsilon \sim \mathcal{N}(0, \sigma_t^2 I)} \| \Sigma \mu - (\Sigma x - \epsilon / \sigma_t^2) \|_2^2 \end{equation}\]

한편, 패치 분포는 확률 변수의 하위 집합에 대한 marginal distribution으로 간주할 수 있다. 패치 분포와 전체 크기 이미지 분포 간의 변환은 marginalization integral이며 간단하다. 가우시안 예제에서 패치 분포는 closed form을 가진다.

\[\begin{equation} p_\mu (x_S) = \mathcal{N}(x \vert P_S \mu, P_S \Sigma P_S^\top) \end{equation}\]

여기서 $S$는 위치와 크기로 식별되는 이미지 패치 내의 픽셀 집합을 나타내고 $P_S$는 $S$와 관련된 selection matrix이다. 그러면 패치 별 score matching은 다음과 같이 쓸 수 있다.

\[\begin{equation} \mathbb{E}_S \mathbb{E}_{x \sim p(x)} \mathbb{E}_{\epsilon \sim \mathcal{N}(0, \sigma_t^2 I)} \| P_S \Sigma \mu - (P_S \Sigma x - \epsilon / \sigma_t^2) \|_2^2 \end{equation}\]

선형 회귀 관점에서 패치 기반 및 전체 크기 score matching 사이의 유일한 차이점은 measurement matrix이다. 언뜻 보기에 patch diffusion은 계산 비용과 균형을 맞바꾸는 것이다. 그러나 저자들은 잘 알려진 이미지 분포의 중복성과 대칭으로 인해 제한된 관찰 하에서 전체 이미지 분포를 복구하는 것이 실제로 가능할 수 있다고 주장한다. 이렇게 하면 patch diffusion이 실제 분포로 수렴될 수 있다.

Experiments

• 데이터셋: CelebA, FFHQ, AFHQv2-Cat/Dog/Wild (모든 데이터셋을 64$\times$64로 resize)
• Implementations: EDM-DDPM++에 Patch Diffusion을 구현

1. Ablation study

다음은 다양한 $p$에 대한 CelebA-64$\times$64의 FID를 나타낸 표와 그래프이다.

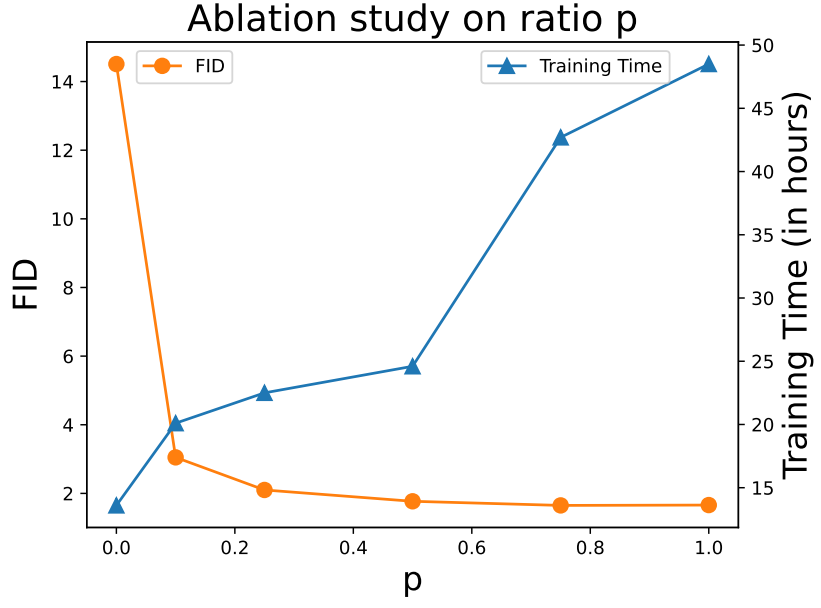
다음은 다양한 $p$로 학습된 모델의 CelebA-64$\times$64에 대한 샘플들이다. (아래로 갈수록 $p$가 증가)

2. Experiments on Large-scale Dataset

다음은 CelebA-64$\times$64과 FFHQ-64$\times$64에 대한 FID, NFE(함수 평가 횟수), 학습시간을 나타낸 표이다.

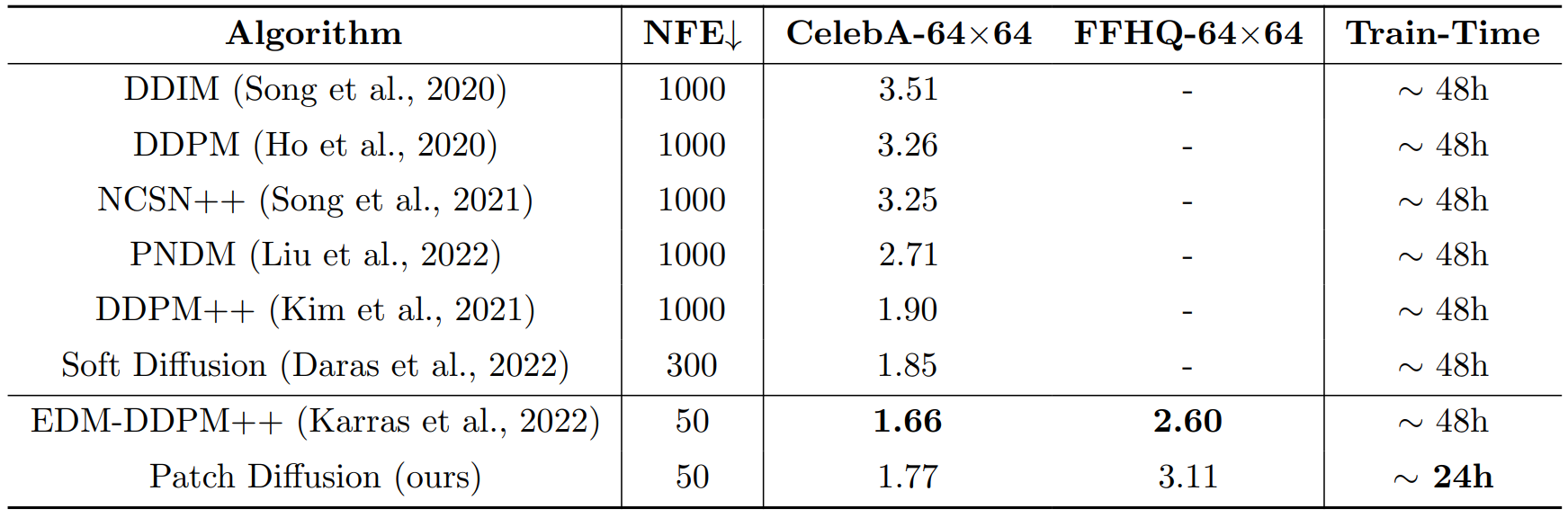
다음은 CelebA-64$\times$64과 FFHQ-64$\times$64에 대한 샘플들이다.

다음은 Patch Diffusion을 Latent Diffusion과 결합한 Latent Patch Diffusion을 LSUN-Bedroom-256$\times$256과 LSUN-Church-256$\times$256에서 평가한 표이다.

3. Experiments on Limited-size Dataset

다음은 제한된 크기의 데이터셋(AFHQv2)에서 Patch Diffusion을 평가한 표이다.

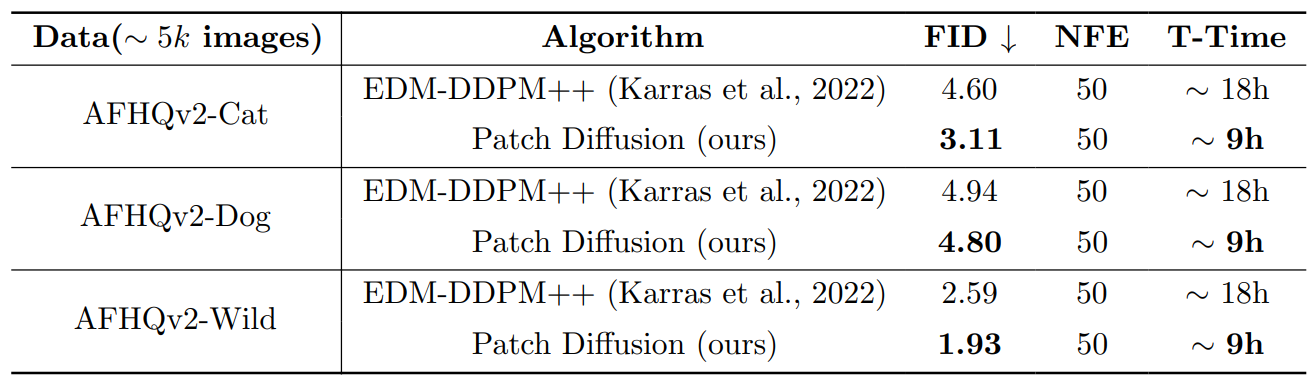
다음은 AFHQv2-64$\times$64에 대한 샘플들이다.