[논문리뷰] Perception Prioritized Training of Diffusion Models (P2 weighting)

CVPR 2022. [Paper] [Github]
Jooyoung Choi, Jungbeom Lee, Chaehun Shin, Sungwon Kim, Hyunwoo Kim, Sungroh Yoon
Data Science and AI Laboratory, Seoul National University | LG AI Research
1 Apr 2022

Introduction

Diffusion model은 denoising score matching loss의 합을 최적화하여 학습된다. Loss의 간단한 합을 사용하는 대신 DDPM 논문은 경험적으로 loss의 가중치 합을 사용하는 것이 샘플 품질에 이점이 있다는 것을 발견하였다. 현재 DDPM의 가중치 목적 함수는 diffusion model을 학습할 때 사실상의 표준 목적 함수로 사용된다.

하지만 놀랍게도 왜 가중치 목적 함수를 사용하는 것이 더 성능이 좋은 지, 샘플 품질에 대하여 최적의 목적 함수인지 등을 알지 못한다. 아직까지 어떤 논문에서도 성능이 더 좋아지는 가중치를 찾는 연구가 진행되지 않았다.

저자들은 더 적합한 가중치를 찾아 가중치 목적 함수의 장점을 더 키우는 것을 목표로 한다. 하지만 적합한 가중치 방법을 디자인하는 것은 다음 2가지 이유 때문에 어렵다.

1. 수천 개의 noise level이 존재하기 때문에 grid search가 불가능하다.
2. 모델이 각 noise level에서 무슨 정보를 학습하는 지가 불분명하여 각 level의 우선순위를 정하기 어렵다.

본 논문에서는 먼저 각 noise level에서 diffusion model이 무엇을 학습하는 지를 확인한다. 저자들의 핵심 아이디어는 손상된 이미지에서 이미지를 복구하는 각 level에 대한 pretext task를 해결하여 풍부한 시각적 개념을 학습한다는 것이다.

이미지가 약간 손상된 noise level에서 이미지는 이미 지각적으로 풍부한 내용을 사용할 수 있으므로 이미지를 복구하는 데 이미지 컨텍스트에 대한 사전 지식이 필요하지 않다. 예를 들어, 모델은 손상된 픽셀을 복구할 때 주변의 손상되지 않은 픽셀을 활용할 수 있다. 따라서 모델은 높은 수준의 컨텍스트가 아닌 인지할 수 없는 세부 정보를 학습한다.

반대로 이미지가 많이 손상되어 내용을 인식할 수 없는 경우, 모델은 주어진 pretext task를 해결하기 위해 지각적으로 인식할 수 있는 내용을 학습한다.

저자들은 이러한 관찰로부터 P2 (perception prioritized) weighting을 제안한다. P2 weighting은 더 중요한 noise level의 pretext task를 우선적으로 해결하는 것을 목표로 한다. 모델이 지각적으로 풍부한 콘텐츠를 학습하는 noise level에서 loss에 더 높은 가중치를 부여하고, 모델이 지각할 수 없는 세부 사항을 학습하는 noise level에서는 최소한의 가중치를 부여한다.

(*pretest task: 연구자들이 일부러 어떤 구실을 만들어서 푸는 문제)

Background

1. Definitions

Diffusion model은 복잡한 데이터 분포 \(p_{data}(x)\)를 간단한 noise 분포 $\mathcal{N}(0, I)$로 변환하며 noise로부터 데이터를 복구하도록 학습된다. Diffusion process는 미리 정의한 noise schedule $0 < \beta_1, \cdots, \beta_T < 1$에 따라 데이터 $x_0$을 점진적으로 손상시킨다. 손상된 데이터 $x_1, \cdots, x_T$는 \(x_0 \sim p_{data}(x)\)로부터 샘플링되며 diffusion process는 다음과 같은 가우시안 transition이다.

\[\begin{equation} q(x_t \vert x_{t-1}) = \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta I) \end{equation}\]

$x_t$는 $x_0$에서 바로 샘플링할 수 있다.

\[\begin{equation} x_t = \sqrt{\alpha_t} x_0 + \sqrt{1- \alpha_t} \epsilon \\ \alpha_t := \prod_{s=1}^t (1-\beta_s), \quad \epsilon \sim \mathcal{N} (0, I) \end{equation}\]

$p(x_T) \sim \mathcal{N}(0,I)$와 diffusion process의 가역성을 보장하기 위해서 $\beta_t$는 작게 설정하여야 하고 $\alpha_T$는 0에 가까워야 한다. DDPM의 경우 $\beta_1$에서 $\beta_T$까지 선형적으로 증가하는 linear noise schedule을 사용하였고, Improved DDPM의 경우 $\alpha_t$가 코사인 함수와 유사한 cosine schedule을 사용하였다.

Diffusion model은 학습된 denoising process $p_\theta (x_{t-1} \vert x_t)$로 $x_0$를 생성하며, denoising process는 diffusion process를 뒤집은 것이다. $x_T \sim \mathcal{N}(0, I)$에서 시작하여 noise predictor $\epsilon_\theta$로 예측된 noise를 순차적으로 뺀다.

\[\begin{equation} x_{t-1} = \frac{1}{\sqrt{1-\beta_t}} (x_t - \frac{\beta_t}{\sqrt{1 - \alpha_t}} \epsilon_\theta (x_t, t)) + \sigma_t z, \quad \quad z \sim \mathcal{N} (0, I) \end{equation}\]

여기서 $\sigma_t^2$은 denoising process의 분산이며 DDPM에서는 $\sigma_t^2$으로 $\beta_t$를 사용한다.

최근 논문에서는 noise schedule을 signal-to-noise ratio (SNR)로 간소화하였다. $x_t$의 SNR은 다음과 같다.

\[\begin{equation} \textrm{SNR}(t) = \frac{\alpha_t}{1 - \alpha_t} \end{equation}\]

이는 $x_0$에서 $x_t$를 샘플링할 때의 평균과 분산의 비를 제곱한 것이다. $\textrm{SNR}(t)$는 단조 감소 함수이다.

2. Training Objectives

Diffusion model은 인코더가 고정된 diffusion process이고 디코더가 학습 가능한 denoising process인 VAE (variational auto-encoder)라고 볼 수 있다. VAE와 비슷하게 VLB (variational lower bound)를 최적화하여 diffusion model을 학습시킬 수 있으며, VLB는 denoising score matching loss의 합이다.

각 step $t$에서 denoising score matching loss $L_t$는 두 가우시안 분포 사이의 거리이다.

\[\begin{aligned} L_t &= D_{KL} (q(x_{t-1} \vert x_t, x_0) \; \| \; p_\theta (x_{t-1} \vert x_t)) \\ &= \mathbb{E}_{x_0, \epsilon} \bigg[ \frac{\beta_t}{(1-\beta_t)(1-\alpha_t)} \| \epsilon - \epsilon_\theta (x_t, t) \|^2 \bigg] \end{aligned}\]

직관적으로 보면 $x_t$에 추가된 noise를 예측하는 신경망 $\epsilon_\theta$를 학습한다.

DDPM은 경험적으로 다음의 단순화된 목적함수가 샘플 품질에 더 이점이 있다는 것을 발견하였다.

\[\begin{equation} L_{simple} = \sum_t \mathbb{E}_{x_0, \epsilon} [\| \epsilon - \epsilon_\theta (x_t, t) \|^2] \end{equation}\]

VLB로 보면 $L_{simple} = \sum_t \lambda_t L_t$은 가중치

\[\begin{equation} \lambda_t = \frac{(1-\beta_t)(1-\alpha_t)}{\beta_t} \end{equation}\]

가 부여된 것으로 생각할 수 있다. 가중치를 SNR로 나타내면 다음과 같다.

\[\begin{equation} \lambda_t = - \frac{1}{\textrm{log-SNR}' (t)} = - \frac{\textrm{SNR}(t)}{\textrm{SNR}'(t)} \\ \textrm{SNR}'(t) = \frac{d \textrm{SNR}(t)}{dt} \end{equation}\]

DDPM이 고정된 $\sigma_t$를 사용한 것과 달리 Improved DDPM은 $\sigma_t$를 하이브리드 목적함수 $L_{hybrid} = L_{simple} + c L_{vlb} (c = 0.001)$로 학습하며, $\sigma_t$를 학습하는 것이 생성 성능을 유지하면서 샘플링 step을 줄일 수 있다고 한다. 따라서 저자들은 이 하이브리드 목적함수를 효율적인 샘플링과 성능 개선을 위해 채택하였다.

Method

1. Learning to Recover Signals from Noisy Data

Diffusion model은 손상된 신호에서 신호를 복구하기 위하여 각 noise level에서 pretest task를 풀어 시각적 개념을 학습한다. 다른 생성 모델이 이미지를 바로 출력하는 것과 달리 diffusion model은 $x_t$에서 noise $\epsilon$를 예측한다. Noise가 컨텐츠나 신호를 포함하지 않기 때문에 어떻게 noise 예측이 풍부한 시각적 개념을 학습하는 데 기여하는 지 이해하기 어렵다. 학습 시 각 step에서 모델이 무슨 정보를 학습하는 지 의문이 생긴다.

Investigating diffusion process

저자들은 먼저 사전 정의된 diffusion process를 분석하여 모델이 각 noise level에서 무엇을 학습하는 지 연구하였다. 두 가지 서로 다른 깨끗한 이미지 $x_0$와 $x_0’$와 noisy한 이미지 $x_{tA}, x_{tB} \sim q(x_t \vert x_0)$와 $x_t’ \sim q (x_t \vert x_0’)$가 있다고 해보자.

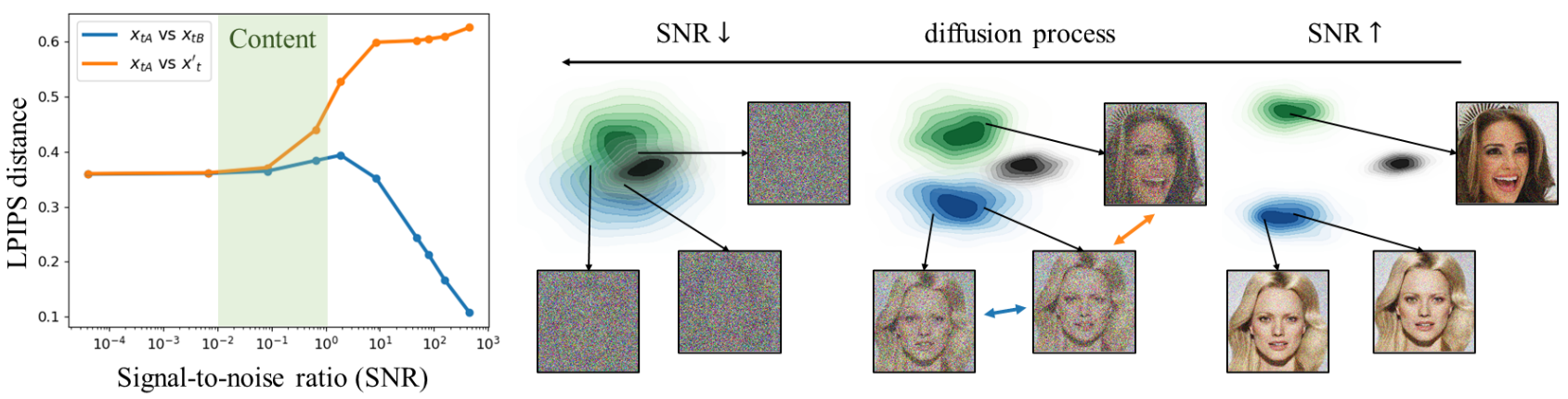
위 그림은 같은 이미지로 합성한 $x_{tA}$와 $x_{tB}$ (파란색)와 다른 이미지에서 합성한 $x_{tA}$와 $x_t’$ (주황색) 사이의 LPIPS 거리를 측정한 것이다.

Diffusion process가 진행됨에 따라 SNR가 감소하고 denoising process가 진행됨에 따라 SNR이 증가한다.

Diffusion process($x_0 \rightarrow x_T$)의 초기 단계에서는 SNR이 크며, 이는 noise가 적고 $x_t$가 $x_0$의 많은 양의 컨텐츠를 유지한다는 것을 의미한다. 따라서 초기 단계에서는 $x_{tA}$와 $x_{tB}$ 사이의 LPIPS가 $x_{tA}$와 $x_t’$ 사이의 LPIPS보다 작다.

모델은 지각적으로 풍부한 신호가 이미 이미지에 준비되어 있으므로 전체적인 맥락을 이해하지 않고도 신호를 복구할 수 있다. 따라서 모델은 SNR이 클 때는 인지할 수 없는 세부 사항만 학습한다.

반대로 나중 단계에서는 SNR이 작으며, 이는 $x_0$의 컨텐츠가 제거될만큼 충분히 큰 noise가 있다는 것을 의미한다. 따라서 두 경우의 LPIPS 거리가 상수로 수렴하며 noisy한 이미지가 복구되기 어렵다.

Noisy한 이미지에 인식 가능한 컨텐츠가 부족하기 때문에 모델은 신호를 복구하기 위하여 사전 지식이 필요하다. 따라서 모델은 SNR이 작을 때는 지갖거으로 풍부한 컨텐츠를 학습한다.

Investigating a trained model

저자들은 학습된 모델을 통해 앞서 언급한 논의를 검증하고자 하였다.

왼쪽 그림과 같이 입력 이미지 $x_0$가 주어지면 먼저 diffusion process $q(x_t \vert x_0)$를 사용하여 $x_t$로 손상시키고 학습된 denoising $p_\theta (x_0 \vert x_t)$로 재구성한다. $t$가 작을 때 재구성 $\hat{x}_0$는 diffusion process가 적은 양의 신호를 제거하기 때문에 입력 $x_0$와 매우 유사하지만 $t$가 클 때 $\hat{x}_0$는 $x_0$와 더 적은 콘텐츠를 공유한다.

오른쪽 그림은 다양한 $t$ 중에서 $x_0$와 $\hat{x}_0$를 비교하여 각 단계가 샘플에 어떻게 기여하는지 보여준다. 처음 두 열의 샘플은 맨 오른쪽 열의 입력과 대략적인 기능 (ex. 전체 색 구성)만 공유하는 반면 3번째와 4번째 열의 샘플은 지각적으로 구별되는 콘텐츠를 공유한다.

이는 모델이 단계 $t$의 SNR이 $10^{-2}$보다 작을 때 거친 특징을 학습하고 모델이 SNR이 $10^{-2}$와 $10^0$ 사이일 때 컨텐츠를 학습함을 시사한다. SNR이 $10^0$(5번째 열)보다 크면 재구성은 입력과 지각적으로 동일하며, 이는 모델이 지각할 수 없는 세부 사항을 학습함을 시사한다.

위의 실험 내용을 기반으로 저자들은 diffusion model이 작은 SNR ($0$ ~ $10^{-2}$)에서 coarse한 특성을 학습하고, 중간 SNR($10^{-2}$ ~ $10^0$)에서 지각적으로 풍부한 컨텐츠를 학습하고, 큰 SNR ($10^0$ ~ $10^4$)에서 남은 noise를 제거한다고 가설을 세웠다. 가설에 따라 coarse stage, content stage, clean-up stage로 noise level을 3단계로 나누었다.

2. Perception Prioritized Weighting

본 논문에서는 Perception Prioritized (P2) weighting을 제안하며 이는 더 중요한 noise level을 학습의 우선순위로 두는 것이 목적이다. 불필요한 clean-up stage에는 최소한의 가중치를 할당하여 나머지에 상대적으로 더 높은 가중치를 할당한다. 특히 모델이 지각적으로 풍부한 컨텍스트를 학습하도록 장려하기 위해 content stage에서 학습을 강조하는 것을 목표로 한다. 이를 위해 다음과 같은 가중치를 구성한다.

\[\begin{equation} \lambda_t' = \frac{\lambda_t}{(k + \textrm{SNR}(t))^\gamma} \end{equation}\]

$\lambda_t$는 기존에 많이 사용하는 DDPM의 가중치이다. $\gamma$는 눈에 띄지 않는 디테일들에 대한 down-weighting의 강도를 조절하기 위한 hyperparameter이다. $k$는 가중치가 굉장히 작은 SNR에 대하여 폭발적으로 커지는 것을 방지하기 위한 hyperparameter이며 가중치의 뾰족한 정도를 결정한다. 여러 디자인이 가능하지만 간단한 P2 weighting이 $\lambda_t$를 가중치로 사용한 것보다 성능이 우수하다고 한다.

사실 $\lambda_t’$은 DDPM의 가중치 $\lambda_t$를 일반화한 것으로, $\gamma = 0$에 가까워질 때 $\lambda_t’$는 $\lambda_t$에 가까워진다.

3. Effectiveness of P2 Weighting

DDPM과 Improved DDPM의 목적 함수 $\sum_t \lambda_t L_t$는 VLB의 목적 함수 $\sum_t L_t$와 다르게 샘플 품질에 대한 더 좋은 inductive bias를 제공한다.

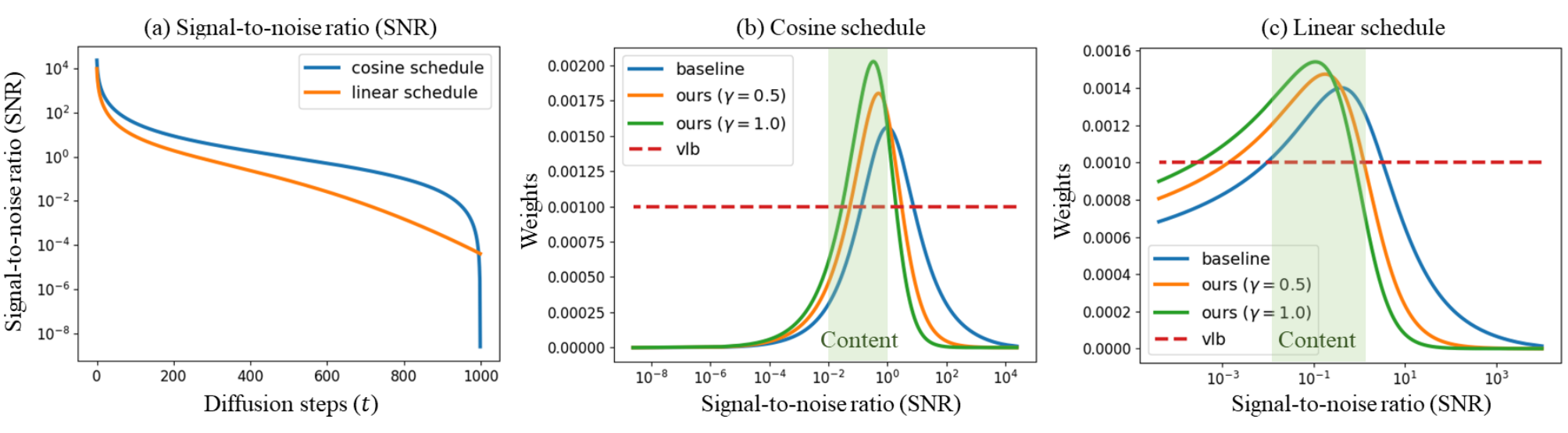
위 그림은 linear noise schedule과 cosine noise schedule 모두에 대한 $\lambda_t’$와 $\lambda_t$를 보여준다. 두 가중치 모두 content stage에서 학습이 가장 많이 집중되며 cleaning stage에서 학습이 가장 적게 집중된다.

$\lambda_t$가 좋은 성능을 내지만 여전히 눈에 띄지 않는 디테일들을 학습하는 데 집중하고 풍부한 컨텐츠를 학습하는 것을 막고 있다.

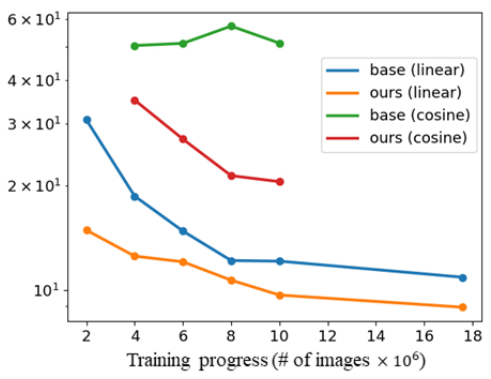
위 그래프는 P2 weighting ($\gamma = 1$)을 사용하였을 때 학습하는 동안의 FID를 나타낸 것이다. Linear noise schedule과 cosine noise schedule 모두 P2 weighting을 사용하였을 때 FID가 감소하였다.

위 그래프에서 또 다른 주목할만한 결과는 비록 P2 weighting이 FID를 큰 차이로 개선하지만 cosine schedule이 큰 차이로 linear schedule보다 성능이 좋지 않다는 것이다. $L_t$ 식은 가중치가 noise schedule과 밀접한 관련이 있음을 나타낸다. Cosine schedule은 linear schedule에 비해 content stage에 더 작은 가중치를 할당한다. 가중치와 noise schedule은 상관관계가 있지만 동등하지 않다. 왜냐하면 noise schedule이 가중치와 MSE 항 모두에 영향을 미치기 때문이다.

정리하면, P2 weighting은 coarse stage와 content stage의 가중치는 키우고 clean-up stage의 가중치는 줄여 풍부한 시각적 컨셉을 학습하는 데 좋은 inductive bias를 제공한다.

4. Implementation

본 논문에서는 쉽게 P2 weighting을 적용하기 위하여 $k = 1$으로 설정한다. 왜냐하면

\[\begin{equation} \frac{1}{1 + \textrm{SNR}(t)} = 1 - \alpha_t \end{equation}\]

이기 때문이다. 경험적으로 2보다 큰 $\gamma$의 경우 clean-up stage의 가중치가 0에 가까워져 샘플에 noise가 많아진다.

모든 실험에서 $T = 1000$으로 설정하였으며 잘 디자인된 아키텍처와 효율적인 샘플링을 제공하는 ADM (논문리뷰) 모델을 사용하였다.

Experiment

P2 weighting을 사용하여 FFHQ, CelebA-HQ, MetFaces, AFHQ-Dogs, Oxford Flowers, CUB Bird 데이터셋에서 생성한 샘플들은 다음과 같다.

1. Comparison to the Baseline

Quantitative comparison

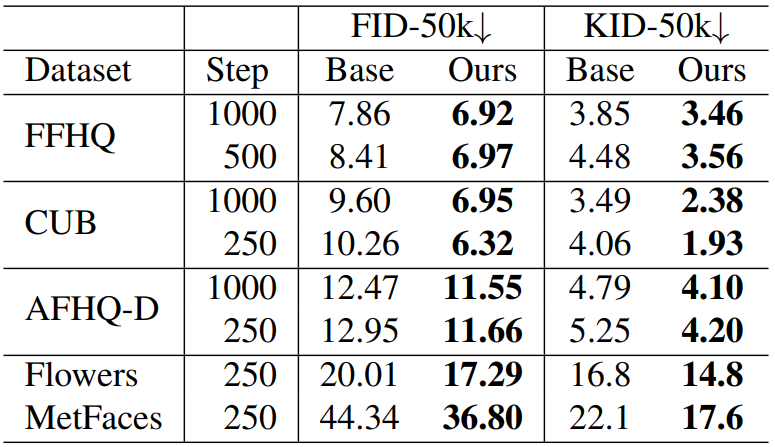
P2 weighting이 FID와 KID 모두에서 더 우수한 성능을 보인다. 이는 P2 weighting이 학습을 위한 좋은 inductive bias를 제공했다고 생각할 수 있다. 특히 1000개의 이미지만을 포함하는 MetFaces 데이터셋에서 크게 성능이 개선되었다. 따라서 제한된 데이터로 학습하는 경우, 눈에 띄지 않는 디테일들을 학습하는 데에 모델의 capacity가 낭비되는 것이 굉장히 해롭다고 할 수 있다.

Qualitative comparison

Baseline 목적 함수로 학습시킨 경우 color shift가 발생한다. 저자들은 baseline 목적 함수가 불필요하게 눈에 띄지 않는 디테일들에 집중했다고 가정하며, 그렇기 때문에 전체 색 구성을 학습하는 데 실패했다고 말한다. 반대로 P2 weighting의 목적 함수는 모델이 데이터셋의 전체적인 컨셉을 학습하도록 한다.

2. Comparison to the Prior Literature

다음은 256$\times$256에 대하여 기존 논문들의 모델과 비교한 결과이다. $T = 1000$으로 샘플링하였다.

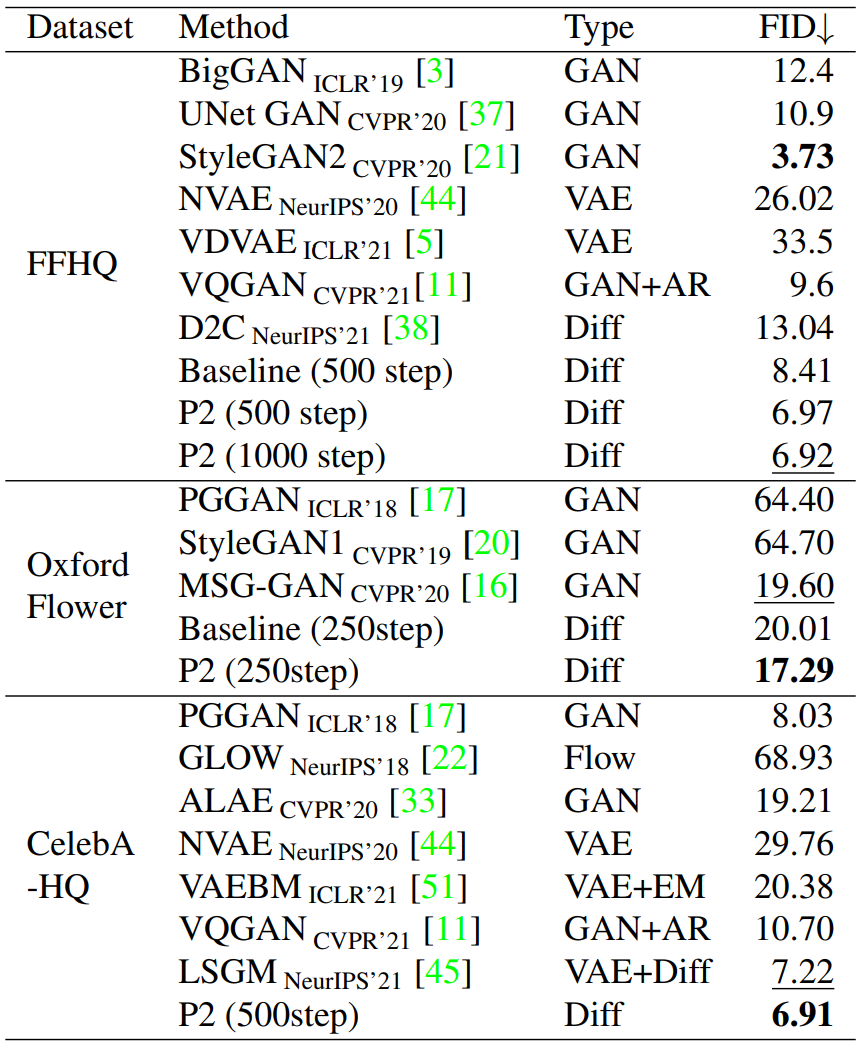
3. Analysis

Model configuration matters?

다음은 여러 설정에 대한 비교이다.

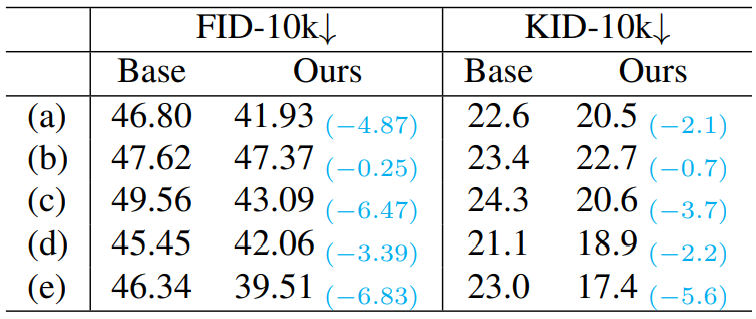
(a)는 기본 설정, (b)는 BigGAN block이 없는 경우, (c)는 Self-attention을 8$\times$8에서만 사용하는 경우, (d)는 residual block이 2개인 경우, (e)는 learning rate가 $2.5 \times 10^{-5}$인 경우이다. 샘플은 250 step으로 생성되었다.

Self-attention을 제거한 경우에 P2 weighting가 가장 효과적이었다. 이는 P2가 global dependency를 학습함을 의미한다.

Sampling step matters?

다음은 샘플링 step 수에 대한 FID 변화를 나타낸 그래프이다.

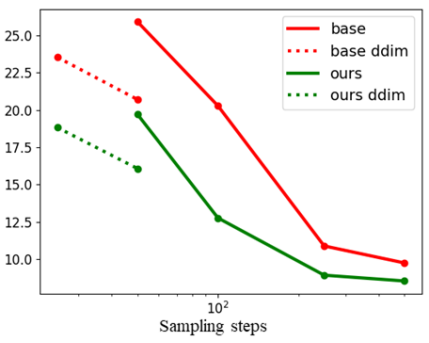
샘플링 step 수를 줄여도 P2 weighting을 사용하였을 때 FID가 더 낮은 것을 볼 수 있다.

Why not schedule sampling steps?

다음은 샘플링 step을 sweep한 것이다.

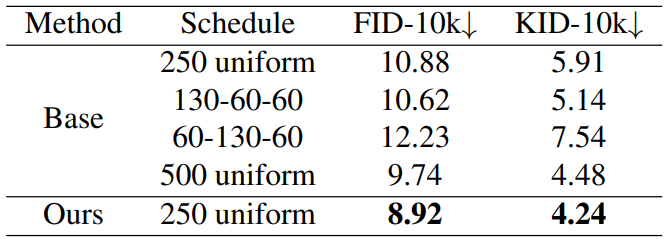
샘플링 step을 sweep하면 FID가 개선되지만 P2 weighting이 더 많이 개선된다.