[논문리뷰] Over-Tokenized Transformer: Vocabulary is Generally Worth Scaling

ICML 2025. [Paper] [Github]
Sean Wu, Shamik Basu, Tim Broedermann, Luc Van Gool, Christos Sakaridis
ETH Zurich | University Of Bologna | INSAIT
28 Jan 2025

Introduction

최근 LLM의 tokenization은 scaling law와 관련이 있는 것으로 밝혀졌다. 즉, 더 큰 모델일수록 더 많은 vocabulary를 필요로 하며 동일한 학습 비용에서 더 나은 성능을 달성할 수 있다. 실제로 입력 vocabulary를 확장해도 추가적인 계산 비용은 거의 발생하지 않지만, 출력 vocabulary를 확장하면 작은 모델의 학습 오버헤드가 크게 증가한다. 따라서 입력 vocabulary와 출력 vocabulary를 분리하여 별도의 연구를 수행하는 것이 자연스러우며, 본 논문은 근본적으로 이러한 아이디어에 기반한다.

저자들은 Context-Free Grammar(CFG)에 대한 실험을 통해 다양한 규모의 모델에 대한 토큰 세분성과 vocabulary 크기의 영향을 체계적으로 분석했다.

1. Tokenizer의 크기가 클수록 더 큰 모델의 성능이 향상되는 반면, 작은 모델에서는 어려움을 겪는다.
2. 입력 vocabulary와 출력 vocabulary가 분리된 후에는 입력 vocabulary만 확장하는 것이 모델 개선에 도움이 되는 반면, 출력 vocabulary가 커지면 작은 모델에 해로울 수 있다.

이러한 통찰력은 인코딩 vocabulary와 디코딩 vocabulary를 분리하여 유연성과 성능 향상을 달성하는 Over-Tokenized Transformers 개발의 동기가 되었다.

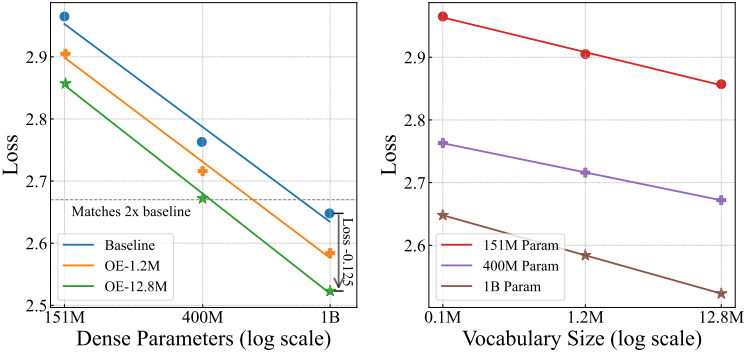
구체적으로, 대규모 계층적 $n$-gram 입력 vocabulary를 활용하는 Over-Encoding(OE)을 도입한다. 본 방법은 모델 scalability를 크게 향상시킨다. 입력 vocabulary 크기를 128배 증가시키면, 400M 모델이 추가 학습 비용 없이 1B 기준선의 학습 loss와 일치한다. 더욱 흥미로운 점은 입력 vocabulary 크기를 지수적으로 증가시키면 loss가 선형적으로 감소한다는 것이다. 이러한 결과는 scaling law의 새로운 차원을 제시하며, 임베딩 파라미터가 새로운 scaling 가능한 차원임을 시사한다.

또한, 저자들은 더 큰 출력 vocabulary를 활용하여 더욱 세밀한 감독을 제공하는 Over-Decoding (OD) 개념을 제안하였다. 본 논문에서는 일반적으로 multi-token prediction 방법을 OD의 근사로 취급한다. 저자들은 over-encoding과 over-decoding을 결합하여 Over-Tokenized Transformer를 구축했는데, 이는 둘 중 하나만 적용하는 것보다 더 큰 잠재력을 보여주었다.

Over-encoding에 많은 양의 임베딩 파라미터를 도입했지만, 임베딩 파라미터가 매우 sparse하게 사용되기 때문에 학습 및 inference 비용은 거의 증가하지 않는다. 저자들은 대규모 vocabulary로 인해 발생하는 계산 및 메모리 문제를 완화하는 효율적인 엔지니어링 솔루션을 제안하였며, 그 결과 추가 학습 오버헤드가 5% 미만으로 감소하였다.

Method

1. Insights from Synthetic Experiments

저자들은 Context-Free Grammar (CFG)을 대상 언어로 사용하여 최대 729자 길이의 3개의 서로 다른 문자로 구성된 시퀀스를 생성했다. 이 설정을 통해 실제 언어 분포를 완전히 파악할 수 있으므로 언어 ​​모델을 정확하게 평가할 수 있다. 저자들은 CFG에서 생성된 샘플에 대해 next-token prediction loss를 사용하여 다양한 크기의 GPT-2 모델을 학습시키고, 유효 생성 비율을 측정하는 모델 생성 시퀀스의 정확도를 기반으로 모델을 평가했다.

첫 번째 실험은 다양한 세분성 수준의 tokenizer를 사용하는 언어 모델의 성능을 비교하는 것을 목표로 하였다. Baseline tokenizer는 CFG에서 정의한 3개의 문자를 사용하여 vocabulary를 구성하고, 문장을 문자 단위로 tokenize하는데, 이를 1-gram tokenizer라고 한다. 또한, n개의 연속된 문자의 가능한 조합 $3^n$개로 구성된 vocabulary를 갖는 $n$-gram tokenizer를 정의한다. 두 tokenizer를 각각 사용하여 크고 작은 GPT-2 모델을 모두 학습시켰다.

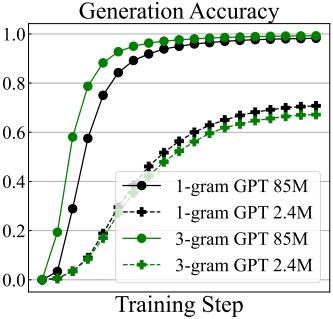
위 그림에서 볼 수 있듯이, tokenizer의 크기가 클수록 더 큰 모델의 성능은 향상되지만, 작은 모델에는 부정적인 영향을 미치는 것을 확인할 수 있다. 특히, tokenizer의 크기가 클수록 학습 시퀀스가 ​​짧아져 학습 비용이 크게 절감된다. 따라서 3-gram tokenizer를 사용하여 더 큰 모델을 학습시키면 학습 비용이 절감될 뿐만 아니라 모델 성능도 향상된다. 직관적인 통찰력은 더 큰 모델이 더 많은 vocabulary를 사용할수록 학습 효율성과 성능이 향상된다는 것이다.

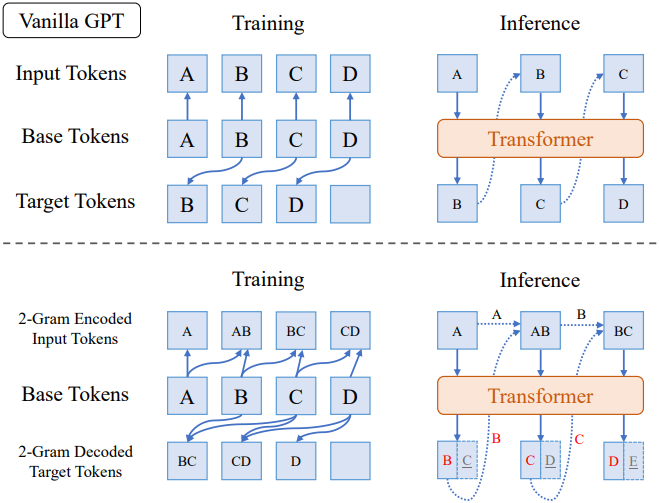
입력 vocabulary와 출력 vocabulary의 확장에 따른 영향을 분리하기 위해, 위 그림과 같이 $n$-gram 인코딩 모델과 $n$-gram 디코딩 모델을 별도로 도입한다. 먼저, 텍스트는 1-gram tokenizer를 통해 문자별로 tokenize된다. $n$-gram 인코딩 모델에서 입력 토큰은 입력 layer에서 $n$-gram 토큰으로 변환되어 크기가 $3^n$인 큰 입력 vocabulary를 생성하고, unembedding layer는 1-gram으로 유지되어 다음 문자 하나를 예측한다. $n$-gram 디코딩 모델에서 입력은 1-gram 토큰으로 유지되고 타겟 레이블, 즉 다음 토큰은 $n$-gram 레이블로 변환되어 다음 $n$개 토큰의 조건부 결합 분포를 예측하는 세분화된 classification head를 생성한다. 두 모델 모두 학습 시퀀스 길이는 변경되지 않고 1-gram tokenizer에서 생성된 길이와 일치한다.

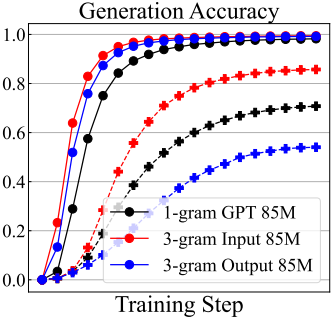
비슷한 inference 비용을 유지하기 위해, inference 중에 $n$-gram 디코딩 모델은 $n$개의 토큰을 동시에 생성하지 않는다. 대신, $n$-gram 예측을 샘플링하지만 다음 1개의 토큰만 보존하고 나머지 토큰 예측은 무시한다. 위 그림은 $n = 3$에 대한 결과이며, 두 모델은 서로 다른 동작을 보인다. 3-gram 인코딩 모델은 모든 모델 크기에서 지속적으로 성능을 향상시킨다. 그러나 3-gram 디코딩 모델은 큰 모델의 성능을 향상시키지만, 작은 모델의 성능을 저하시킨다.

저자들은 대규모 입력 vocabulary는 항상 좋은 반면, 대규모 출력 vocabulary는 작은 모델에서는 나쁠 수 있다는 결론을 내렸다. 이러한 차이는 각각의 역할에 있다. 입력 임베딩은 컨텍스트를 feature 임베딩으로 인코딩하는 역할을 하며, vocabulary가 클수록 feature 매핑의 표현 능력이 향상되어 모델에 긍정적인 영향을 미친다. 반면, 출력 vocabulary는 예측의 세분성을 결정한다. 출력 vocabulary가 클수록 더욱 세분화된 학습 신호가 필요하게 되는데, overfitting되기 쉬운 큰 모델에서는 유익할 수도 있고, 심각한 underfitting이 발생하는 작은 모델에서는 부담스러울 수도 있다.

이러한 관찰 결과를 바탕으로, 본 논문에서는 실제 자연어 모델링에서 over-tokenized transformer에 대한 연구를 확장하였다.

2. Over-Tokenized Transformer

기본 tokenizer의 vocabulary 크기가 $V$라면 (보통 $10^5$), 크기가 $V^n$ 인 $n$-gram vocabulary는 지나치게 커지고 비실용적이 된다는 문제가 발생한다. 이 문제를 해결하기 위해, 저자들은 일련의 행렬 분해를 통해 큰 임베딩 테이블을 근사화하는 방법을 제안하였다.

기본 tokenizer에서 입력 ID 시퀀스 $x_1, \ldots, x_t$가 ​​주어지면 다음과 같이 $n$-gram 입력 토큰 $x_i^{(-n)}$를 정의한다.

\[\begin{equation} x_i^{(-n)} = f (x_i, x_{i-1}, \ldots, x_{i-n+1}) \end{equation}\]

여기서 $f(z_1, \ldots, z_n)$은 인덱스 매핑 함수이고, 범위를 벗어난 인덱스는 0 토큰으로 패딩된다. 한 가지 직관적인 설계는 $(z_1, \ldots, z_n)$을 $p$진수 숫자로 취급하고 $f$를 다음과 같이 정의하는 것이다.

\[\begin{equation} f(z_1, \ldots, z_n) = \sum_{i=1}^n z_i p^{i-1} \end{equation}\]

여기서 $p \ge V$이면 $f$는 전단사 함수이다. 일반적으로 $f$의 범위를 최대한 작게 유지하기 위해 $p$를 $V$로 설정한다. $x_i^{(−1)} = x_i$는 표준 transformer 입력에 해당한다.

일반적인 $n$-gram embedder

유연한 $n$-gram embedder 모듈을 설계하는 핵심은 vocabulary 크기 $m$을 설정 가능하도록 만드는 것이다. 저자들은 간단한 tiled matrix parameterization 방식을 사용하여 이를 효율적으로 달성하였다. 구체적으로, tiled matrix parameterization은 $m \times d$ 크기의 임베딩 테이블을 타일링을 통해 $V^n \times d$ 크기의 임베딩 테이블로 확장한다. 실제로 lookup 과정은 간단하다. 입력 토큰 $x^{(n)}$은 m에 대한 나머지 연산으로 매핑된다.

\[\begin{equation} \textbf{h} = \textbf{E} (x^{(n)} \; \% \; m) \end{equation}\]

($\textbf{h}$는 출력 임베딩, $\textbf{E} \in \mathbb{R}^{m \times d}$는 임베딩 행렬)

이 $n$-gram $m \times d$ embedder를 \(\mathbb{E}^{m \times d} (x^{(n)})\)로 나타낸다.

Over-Encoding (OE)

저자들은 계층적 인코딩 패러다임이 매우 효과적임을 확인했다. 구체적으로, GPT 모델에 대한 입력 임베딩을 1-gram, 2-gram, …, $n$-gram 임베딩의 합으로 계산했다. 또한, 더 작은 임베딩 차원을 사용함으로써 얻을 수 있는 추가적인 이점을 관찰했다. Embedder $\mathbb{E}_n^{m \times d}$은 다음과 같이 표현되는 $k$개의 low-rank decomposition된 embedder로 분할될 수 있다.

\[\begin{equation} \mathbb{E}^{m \times d \vert k} (x^{(-n)}) = \sum_{i=1}^k \mathbb{E}_i^{m \times \frac{d}{k}} (x^{(-n)}) \textbf{W}_i \end{equation}\]

\(\textbf{W}_i \in \mathbb{R}^{\frac{d}{k} \times d_\textrm{model}}\)는 임베딩 벡터를 모델 차원에 맞게 projection한다. 동일한 수의 임베딩 파라미터를 사용하고 $k$개의 행렬 \(\textbf{W}_i\)를 통해 최소한의 추가 비용만 발생하므로 이 접근 방식은 성능을 크게 향상시킨다.

전반적으로, over-encoding 프로세스는 입력 토큰을 다음과 같이 임베딩에 매핑한다.

\[\begin{equation} \textrm{OE}(x) = \mathbb{E}^{V \times d} (x^{(-1)}) + \sum_{i=1}^n \mathbb{E}^{m \times \frac{d}{n} \vert k} (x^{(-i)}) \end{equation}\]

여기서 1-gram 임베딩 \(\mathbb{E}^{V \times d} (x^{(-1)})\)은 원래 Transformer와 일관되게 구현된다. 일반적으로 $m$은 $V$보다 훨씬 큰 값으로 설정되며, $m$이 증가함에 따라 모델 성능이 지속적으로 향상된다.

특히, $m$개의 행을 가진 여러 embedder의 경우, 각 embedder가 고유한 매핑을 갖도록 작은 조정을 수행한다 (ex. $m$을 $m + 2$로 대체). 이렇게 하면 임베딩의 조합 용량이 증가한다. 그렇지 않으면 슬라이스 기법이 아무런 효과를 발휘하지 못할 것이다.

Over-Decoding (OD)

CFG 실험 결과를 보면, 추가 토큰 디코딩은 충분히 큰 모델에서만 효과적이다. 실제로 multi-token prediction (MTP)에 대한 기존 논문들은 일반적으로 over-decoding의 근사이며, 대규모 모델만이 미래 토큰 예측의 이점을 얻는다는 동일한 결론을 공유한다. 일반적으로 본 논문에서는 MTP 유사 방법을 over-decoding으로 간주한다.

Over-Tokenized Transformer (OT)

Over-encoding과 over-decoding을 통합하여 over-tokenized transformer를 얻는다. 특히, 저자들은 DeepSeek V3에서 제안된 MTP의 조건부 재귀적 형태인 MTP-DS에 초점을 맞추었다. MTP는 더 이상 다음 몇 개의 토큰을 병렬로 예측하지 않고 순차적으로 예측한다. $n$번째 head의 경우, 다음 $(n-1)$번째 토큰의 임베딩은 다음 $n$번째 토큰 예측의 조건으로 레이어 입력에 concat된다.

MTP-DS 아키텍처에서 over-encoding은 토큰 임베딩의 표현 용량을 향상시키고 미래 토큰 예측에 직접적으로 관여한다. 한편으로는 미래 토큰 예측에 대한 학습이 더 쉬워지고, 다른 한편으로는 over-encoding을 더욱 충분히 학습시킬 수 있다. 이러한 장점들을 바탕으로, 두 방법을 통합하면 비교적 작은 모델에서도 더 큰 이점을 얻을 수 있다.

3. Engineering Challenges and Solutions

Over-encoding은 매우 큰 입력 vocabulary를 생성한다. 이론적으로 임베딩은 토큰 ID를 기반으로 sparse하게 접근되므로 vocabulary를 확장하더라도 학습 또는 inference 비용에는 거의 영향을 미치지 않는다. 그러나 큰 임베딩 파라미터는 GPU에 상당한 메모리 부담을 줄 수 있다. 또한, FSDP와 같은 파라미터 샤딩 전략을 학습 중에 적용할 경우, 이러한 sparse 파라미터의 통신으로 인해 학습 효율성이 심각하게 저하되어 vocabulary 크기 $m$의 선택이 더 작은 값으로 제한될 수 있다.

이 문제를 완화하기 위해, 통신 오버헤드를 줄이기 위해 over-encoding 임베딩 layer에 텐서 병렬 처리를 사용한다. 임베딩 테이블은 모든 data-parallel (DP) rank에 걸쳐 행 단위로 샤딩된다. 주어진 입력에 대해 토큰은 임베딩을 보유한 해당 DP rank로 전송되고, 임베딩 벡터를 쿼리한 후, 결과 임베딩을 원래 DP rank로 다시 전송한다. 이 프로세스는 forward pass 동안 두 번의 all-to-all 통신과 backward pass 동안 한 번의 all-to-all 통신을 포함하며, 결과적으로 FSDP보다 총 통신량이 훨씬 적다.

Experiments

• 구현 디테일
  • baseline: OLMo2-1B
  • $n = 3$
  • vocabulary size: $m = 1.28 \times 10^7$
  • $\frac{d_\textrm{model}}{nk} \approx 256$이 되도록 $k$를 설정

1. Over-Encoding Scaling Trend

다음은 baseline인 OLMo2-1B와 학습 곡선을 비교한 것이다.

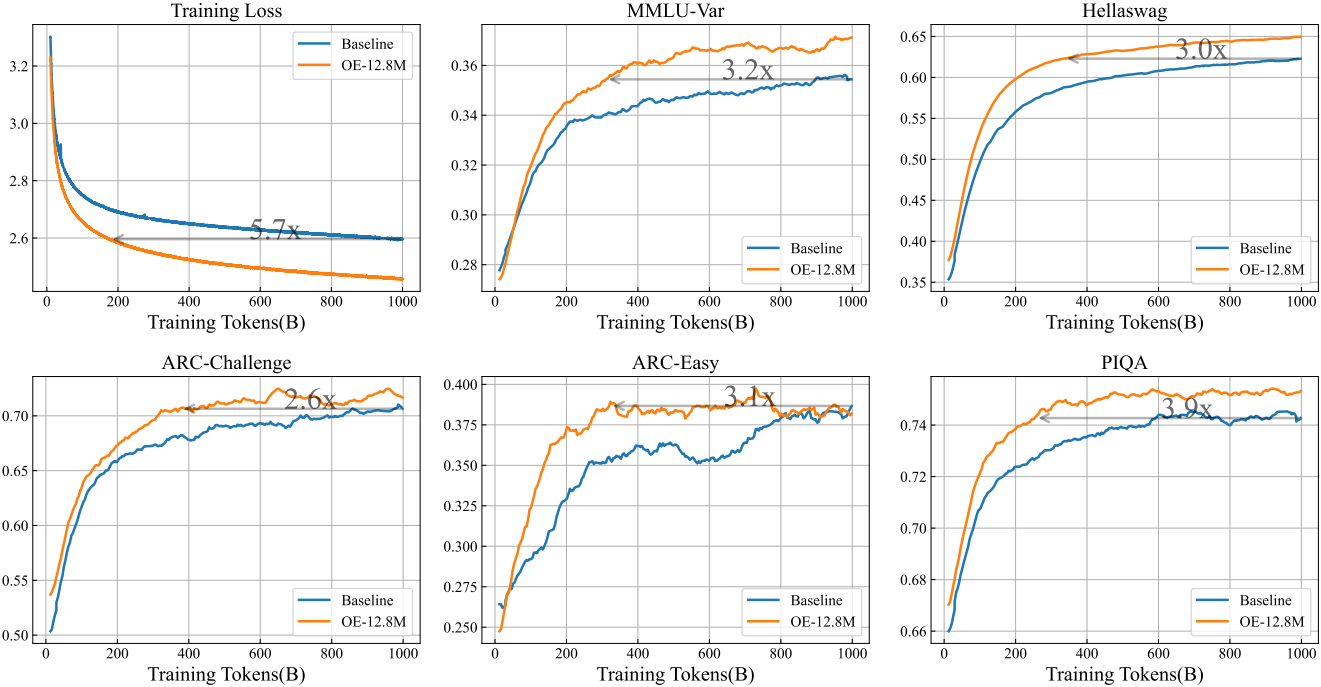
다음은 MoE 아키텍처에 대한 over-encoding의 성능을 비교한 것이다.

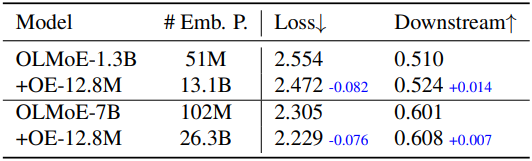
2. Ablation Study

다음은 vocabulary 크기 $m$과 학습 loss 사이의 관계를 나타낸 그래프이다.

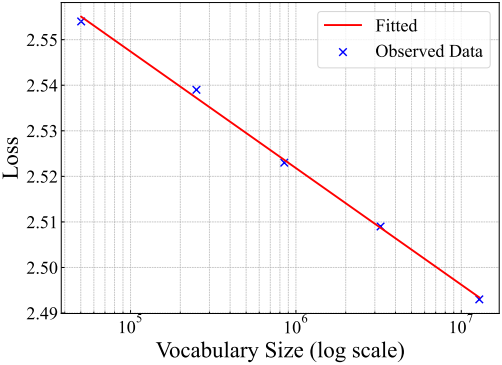
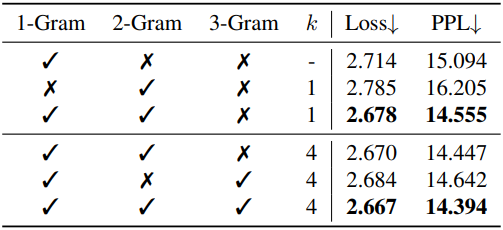
다음은 vocabulary 디자인에 대한 ablation study 결과이다.

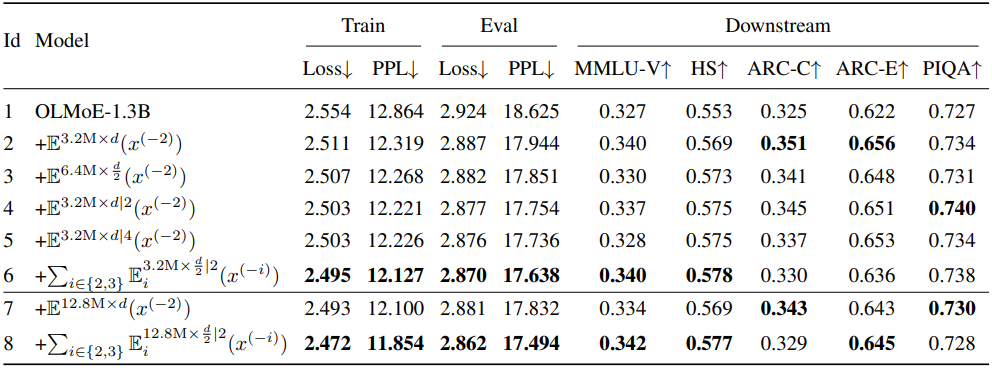
다음은 over-encoding의 계층적 디자인에 대한 ablation study 결과이다.

3. Over-Tokenized Transformer

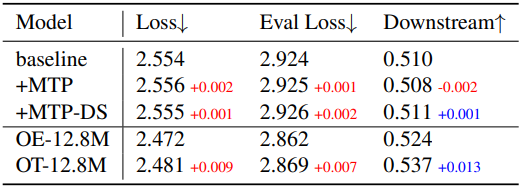
다음은 OLMoE-1.3B에 대한 MTP 실험 결과이다.

4. Speed Analysis

다음은 (왼쪽) 처리량과 (오른쪽) forward pass에서의 토큰당 GFLOPs를 비교한 표이다.

다음은 inference 속도를 비교한 표이다.