[논문리뷰] Optimal Projection for 3D Gaussian Splatting
ECCV 2024. [Paper]
Letian Huang, Jiayang Bai, Jie Guo, Yanwen Guo
Nanjing University
1 Feb 2024

Introduction
Novel view synthesis는 알려진 카메라 파라미터를 사용하여 일련의 이미지를 보간하여 3D 장면 또는 물체의 새로운 뷰를 생성하는 것을 목표로 한다. 이 분야에서는 MLP를 기반으로 한 NeRF의 출현으로 상당한 발전이 이루어졌다. 그러나 NeRF는 MLP에 의존하므로 학습 및 렌더링 시간이 길어지고 여전히 실시간 렌더링이 상당히 어렵다. 결과적으로 많은 방법이 가속을 위해 보조 데이터 구조에 의존한다. 그러나 장면의 implicit한 표현과 광선을 따른 dense한 포인트 샘플링으로 인해 여전히 실시간 성능을 달성하는 데 어려움을 겪고 있다.
최근 3D Gaussian Splatting(3D-GS)은 MLP를 사용한 implicit한 장면 표현에서 벗어나 대신 Gaussian을 사용한 explicit한 표현을 선택했다. 이 접근 방식은 렌더링 통합을 위해 ray marching을 하는 동안 샘플링 포인트가 필요하지 않으며 이를 이미지 공간에 대한 유한한 Gaussian splatting으로 대체하고 실시간 렌더링을 달성하였다. 최근에는 3D-GS의 sparse-view 시나리오에서의 robustness, 성능, 저장 효율성을 향상시키려는 노력이 진행되고 있다. 그러나 이러한 개선 노력은 Gaussian projection 자체와 관련된 오차를 구체적으로 해결하지 못했다. Gaussian 개선과 관련된 잠재적인 방법은 Mip-Splatting이다. 그러나 projection 함수와 projection 오차를 조사하지 않고 Gaussian 필터를 도입하였으며, 여전히 $z = 1$ 평면에 projection하는 데 의존한다.
NeRF와 유사하게 3D-GS에 대한 입력은 SfM으로 보정된 카메라와 이미지 세트로 구성된다. 그러나 NeRF와 달리 3D-GS는 SfM 프로세스 중에 생성된 sparse한 포인트 클라우드를 입력으로 사용한다. 이러한 포인트들에서 장면을 명시적으로 나타내는 기본 요소로 3D Gaussian 집합을 구성한다. 각 3D Gaussian은 위치(평균) $\boldsymbol{\mu}$, 공분산 행렬 $\boldsymbol{\Sigma}$, 불투명도 $\alpha$를 속성으로 가지며, 방향에 따른 색상을 나타내는 spherical harmonics(SH)를 가진다. 이후, 이러한 3D Gaussian들은 미분 가능한 rasterization을 위해 projection 함수 $\phi$를 통해 이미지 평면($z = 1$ 평면)에 projection된다. 이 프로세스는 NeRF 기반 방법에 비해 상당한 성능 향상을 가져오며 실시간 렌더링을 달성하였다.
안타깝게도 Gaussian은 convolution이나 affine transformation을 통해 Gaussian 속성을 유지함에도 불구하고 projection transformation을 거친 후에 반드시 그러한 특성을 유지하지 못할 수도 있다. 따라서 3D-GS는 local affine approximation을 채택하며, 특히 테일러 전개의 처음 두 항으로 projection 함수를 근사화한다. 그럼에도 불구하고 이러한 근사는 오차를 발생시키며, 렌더링된 이미지에서 아티팩트를 유발할 수 있다. 본 논문에서는 테일러 전개의 나머지 항을 분석하여 3D-GS의 오차와 Gaussian 평균 사이의 관계를 활용한다. 또한 오차 함수의 극한값을 결정하여 오차가 최소화되는 상황을 식별하였다.
저자들은 오차 함수에 대한 극한분석을 바탕으로 Optimal Projection을 제안하였다. 구체적으로, Gaussian 평균에서 카메라 중심 방향을 따라 projection한다. 여기서 projection 평면은 Gaussian 평균과 카메라 중심을 연결하는 선에 접한다. 저자들은 다양한 데이터셋에서 제안된 projection을 $z = 1$ 평면에 3D Gaussian을 projection하는 간단한 접근 방식과 비교하였으며, 결과적으로 오차가 감소하여 실시간으로 사실적인 렌더링이 가능함을 보여주었다.
Preliminaries
월드 좌표계에는 평균이 $\boldsymbol{\mu}$이고 공분산 행렬이 $\boldsymbol{\Sigma}$인 3D Gaussian $G$가 있으면 다음과 같이 표현된다.
\[\begin{equation} G(\textbf{x}) = \exp (-1/2 (\textbf{x} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\textbf{x} - \boldsymbol{\mu})) \end{equation}\]이 Gaussian에는 블렌딩 과정에서 $\alpha$가 곱해진다.
Gaussian을 이미지 평면에 projection하기 위해 3D-GS의 초기 단계에는 viewing transformation matrix $\textbf{W}$를 통해 이 Gaussian을 월드 좌표계에서 카메라 좌표계로의 affine transformation이 포함된다. 변환된 Gaussian은 다음과 같다.
\[\begin{aligned} G(\textbf{x}) &= \exp (-1/2 (\textbf{x} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\textbf{x} - \boldsymbol{\mu})) \\ &= \exp (-1/2 (\textbf{Wx} - \textbf{W} \boldsymbol{\mu})^\top (\textbf{W} \boldsymbol{\Sigma} \textbf{W}^\top)^{-1} (\textbf{Wx} - \textbf{W} \boldsymbol{\mu})) \end{aligned}\]이는 다음과 같이 표현될 수도 있다.
\[\begin{equation} G^\prime (\textbf{x}^\prime) = \exp (-1/2 (\textbf{x}^\prime - \boldsymbol{\mu}^\prime)^\top \boldsymbol{\Sigma}^{\prime -1} (\textbf{x}^\prime - \boldsymbol{\mu}^\prime)) \end{equation}\]여기서 $G^\prime$, $\textbf{x}^\prime = \textbf{Wx}$, $\boldsymbol{\mu}^\prime = \textbf{W} \boldsymbol{\mu}$, $\boldsymbol{\Sigma}^\prime = \textbf{W} \boldsymbol{\Sigma} \textbf{W}^\top$는 각각 카메라 좌표계의 3D Gaussian, 점, 평균, 공분산 행렬이다.
이어서, 카메라 좌표계의 Gaussian을 $z = 1$ 평면에 projection해야 한다. Projection 평면은 다음과 같다.
\[\begin{equation} \textbf{x}_0^\top \cdot (\textbf{x}^\prime - \textbf{x}_0) = 0 \end{equation}\]여기서 \(\textbf{x}_0 = [0, 0, 1]^\top\)은 이 평면에 대한 카메라 좌표계 원점의 projection을 나타낸다. Projection 평면 방정식에 따르면 projection 함수 $\phi$는 다음과 같이 구해진다.
\[\begin{equation} \phi (\textbf{x}^\prime) = \textbf{x}^\prime (\textbf{x}_0^\top \textbf{x}^\prime)^{-1} (\textbf{x}_0^\top \textbf{x}_0) = \textbf{x}^\prime (\textbf{x}_0^\top \textbf{x}^\prime)^{-1} \end{equation}\]테일러 전개를 사용하여 이 projection 함수를 1차로 확장한다.
\[\begin{aligned} \phi (\textbf{x}^\prime) &= \phi (\boldsymbol{\mu}^\prime) + \frac{\partial \phi}{\partial \textbf{x}^\prime} (\boldsymbol{\mu}^\prime) (\textbf{x}^\prime - \boldsymbol{\mu}^\prime) + R_1 (\textbf{x}^\prime) \\ &\approx \phi (\boldsymbol{\mu}^\prime) + \frac{\partial \phi}{\partial \textbf{x}^\prime} (\boldsymbol{\mu}^\prime) (\textbf{x}^\prime - \boldsymbol{\mu}^\prime) \end{aligned}\]여기서 \(\frac{\partial \phi}{\partial \textbf{x}^\prime} (\boldsymbol{\mu}^\prime) = \textbf{J}\)는 projective transformation의 affine approximation의 Jacobian이다. 테일러 전개의 나머지 항을 무시하여 이 local affine approximation을 적용하면 $z = 1$ 평면에 projection된 2D Gaussian $G_\textrm{2D}$를 얻을 수 있다.
\[\begin{aligned} G_\textrm{2D} (\textbf{x}^\prime) &= \exp (-1/2 (\textbf{J} \textbf{x}^\prime - \textbf{J} \boldsymbol{\mu}^\prime)^\top (\textbf{J} \boldsymbol{\Sigma}^\prime \textbf{J}^\top)^{-1} (\textbf{J} \textbf{x}^\prime - \textbf{J} \boldsymbol{\mu}^\prime)) \\ &\approx \exp (-1/2 (\phi (\textbf{x}^\prime) - \phi (\boldsymbol{\mu}^\prime))^\top (\textbf{J} \boldsymbol{\Sigma}^\prime \textbf{J}^\top)^{-1} (\phi (\textbf{x}^\prime) - \phi (\boldsymbol{\mu}^\prime))) \end{aligned}\]행렬 $\textbf{J}$의 rank가 2이므로 $\textbf{J} \boldsymbol{\Sigma}^\prime \textbf{J}^\top$의 역행렬은 실제로 2D Gaussian의 공분산 행렬의 역행렬이며 이는 $\textbf{J}$의 세 번째 행과 열을 건너뛰는 것을 의미한다. 마찬가지로 이 함수는 다른 형식으로 표현될 수 있다.
\[\begin{equation} G_\textrm{2D} (\textbf{x}_\textrm{2D}) = \exp (-1/2 (\textbf{x}_\textrm{2D} - \boldsymbol{\mu}_\textrm{2D})^\top \boldsymbol{\Sigma}_\textrm{2D}^{-1} (\textbf{x}_\textrm{2D} - \boldsymbol{\mu}_\textrm{2D})) \end{equation}\]여기서 $G_\textrm{2D}$, \(\textbf{x}_\textrm{2D} = \phi (\textbf{x}^\prime)\), \(\boldsymbol{\mu}_\textrm{2D} = \phi (\boldsymbol{\mu}^\prime)\), \(\boldsymbol{\Sigma}_\textrm{2D} = \textbf{J} \boldsymbol{\Sigma}^\prime \textbf{J}^\top\)은 이미지 좌표계의 2D Gaussian, 점, 평균, 2$\times$2 공분산이다.
이후 월드 좌표계의 3D Gaussian을 이미지 평면에 projection한다. 그 후, 이미지 평면에 대해 rasterization이 수행되어 렌더링된 이미지를 얻는다.
Local Affine Approximation Error
3D-GS는 projection transformation 중에 근사, 즉 local affine approximation을 도입한다. Rasterization은 3D Gaussian의 실제 projection 함수가 아닌 2D Gaussian을 사용한다. 이 근사에 의해 발생하는 오차는 테일러 전개의 나머지 항으로 나타낼 수 있다.
\[\begin{aligned} R_1 (\textbf{x}^\prime) &= \phi (\textbf{x}^\prime) - \phi (\boldsymbol{\mu}^\prime) - \frac{\partial \phi}{\partial \textbf{x}^\prime} (\boldsymbol{\mu}^\prime) (\textbf{x}^\prime - \boldsymbol{\mu}^\prime) \\ \frac{\partial \phi}{\partial \textbf{x}^\prime} (\boldsymbol{\mu}^\prime) &= \mathbb{I} \otimes (\textbf{x}_0^\top \boldsymbol{\mu}^\prime)^{-1} - \textbf{x}_0 (\textbf{x}_0^\top \boldsymbol{\mu}^\prime)^{-1} (\boldsymbol{\mu}^{\prime \top} \textbf{x}_0)^{-1} \boldsymbol{\mu}^{\prime \top} \end{aligned}\]여기서 $\mathbb{I}$는 단위 행렬, $\otimes$는 행렬과 스칼라의 곱셈이다. 이 테일러 전개의 나머지 항은 확률 변수 $\textbf{x}^\prime$와 Gaussian의 평균 $\boldsymbol{\mu}^\prime$와 관련된 3D 벡터이다. 따라서 이 벡터의 Frobenius norm의 제곱 $\vert \vert R_1 (\textbf{x}^\prime) \vert \vert_F^2$을 계산하고 $\textbf{x}^\prime$에 대한 기대값을 취함으로써 궁극적으로 $\boldsymbol{\mu}^\prime$에만 의존하는 오차 함수를 얻는다.
\[\begin{equation} \epsilon (\boldsymbol{\mu}^\prime) = \int_{\textbf{x}^\prime \in \mathcal{X}^\prime} \| R_1 (\textbf{x}^\prime) \|_F^2 d \textbf{x}^\prime \end{equation}\]오차 함수의 극값을 찾기 전에 적분 표현식을 단순화해 보자. 먼저, $\textbf{x}^\prime$ 및 $\boldsymbol{\mu}^\prime$를 카메라 중심을 중심으로 한 단위 구에 투영된 단위 벡터로 단순화한다. 이는 3차원 공간의 점을 단위 구 $\pi$에 projection한 다음 projection 평면 $\phi$에 투영하는 합성 변환 $(\phi \circ \pi)$가 3차원 공간의 점을 projection 평면에 직접 투영하는 것과 동일하다는 것을 증명하여 단순화된다. 이러한 단순화를 통해 전체 오차 함수에는 세 개의 단위 공간 벡터 사이의 연산만 포함된다. 증명은 다음과 같다.
\[\begin{aligned} (\phi \circ \pi) (\textbf{x}^\prime) &= \phi (\textbf{x}^\prime (\textbf{x}^{\prime \top} \textbf{x}^\prime)^{-1/2}) \\ &= \textbf{x}^\prime (\textbf{x}^{\prime \top} \textbf{x}^\prime)^{-1/2} (\textbf{x}_0^\top (\textbf{x}^\prime (\textbf{x}^{\prime \top} \textbf{x}^\prime)^{-1/2}))^{-1} \\ &= \textbf{x}^\prime (\textbf{x}_0^\top \textbf{x}^\prime)^{-1} \\ &= \phi (\textbf{x}^\prime) \end{aligned}\]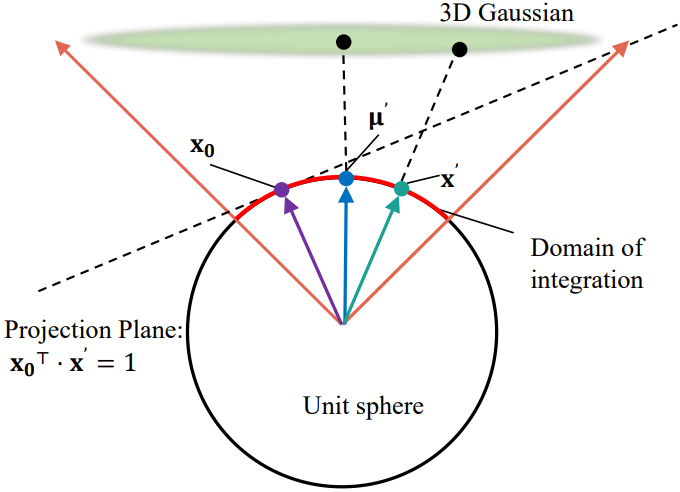
단순화된 오차 함수 $\epsilon$는 위 그림에 표시된 대로 3개의 단위 벡터 또는 단위 구의 3개 점 $\textbf{x}^\prime$, \(\textbf{x}_0\), $\boldsymbol{\mu}^\prime$를 포함한다. 세 점의 구면 좌표는 다음과 같다.
여기서 \(\phi_0 = 0\)이고 \(\theta_0 = 0\)이다. 이를 통해 $\textbf{J}$와 $R_1 (\textbf{x}^\prime)$을 구하면 다음과 같다.
\[\begin{aligned} \textbf{J} &= \begin{bmatrix} \frac{1}{\cos (\phi_\mu) \cos (\theta_\mu)} & 0 & -\frac{\sin (\phi_\mu)}{\cos^2 (\phi_\mu) \cos (\theta_\mu)} \\ 0 & \frac{1}{\cos (\phi_\mu) \cos (\theta_\mu)} & \frac{\sin (\theta_\mu)}{\cos^2 (\phi_\mu) \cos^2 (\theta_\mu)} \\ 0 & 0 & 0 \end{bmatrix} \\ R_1 (\textbf{x}^\prime) &= \begin{bmatrix} -\frac{\sin (\phi -\phi_\mu) \cos(\theta)}{\cos^2 (\phi_\mu) \cos (\theta_\mu)} + \tan (\phi) - \tan (\phi_\mu) \\ \frac{\sin (\theta)}{\cos (\phi_\mu) \cos (\theta_\mu)} - \frac{\sin (\theta_\mu) \cos (\phi) \cos (\theta)}{\cos^2 (\phi_\mu) \cos^2 (\theta_\mu)} + \frac{\tan (\theta_\mu)}{\cos (\phi_\mu)} - \frac{\tan (\theta)}{\cos (\phi)} \\ 0 \end{bmatrix} \end{aligned}\]적분 영역의 크기는 Gaussian의 공분산과 관련이 있다. 현재 논의에서는 분산보다는 평균이 오차에 미치는 영향에 초점을 맞추고 있으므로 적분 영역을 다음과 같이 가정한다.
\[\begin{equation} \{ \textbf{x}^\prime \; \vert \; \theta \in [-\frac{\pi}{4} + \theta_\mu, \frac{\pi}{4} + \theta_\mu] \wedge \phi \in [-\frac{\pi}{4} + \phi_\mu, \frac{\pi}{4} + \phi_\mu] \} \end{equation}\]$R_1 (\textbf{x}^\prime)$ 식을 $\epsilon (\boldsymbol{\mu}^\prime)$ 식에 대입하면 다음과 같다.
\[\begin{aligned} \epsilon (\theta_\mu, \phi_\mu) &= \int_{-\pi/4 + \theta_\mu}^{\pi/4 + \theta_\mu} \int_{-\pi/4 + \phi_\mu}^{\pi/4 + \phi_\mu} \bigg( -\frac{\sin (\phi -\phi_\mu) \cos(\theta)}{\cos^2 (\phi_\mu) \cos (\theta_\mu)} + \tan (\phi) - \tan (\phi_\mu) \bigg)^2 + \\ & \bigg( \frac{\sin (\theta)}{\cos (\phi_\mu) \cos (\theta_\mu)} - \frac{\sin (\theta_\mu) \cos (\phi) \cos (\theta)}{\cos^2 (\phi_\mu) \cos^2 (\theta_\mu)} + \frac{\tan (\theta_\mu)}{\cos (\phi_\mu)} - \frac{\tan (\theta)}{\cos (\phi)} \bigg)^2 d \theta d \phi \end{aligned}\]이 함수는 $\theta_\mu$와 $\phi_\mu$에 대해 편미분된다. $\theta_\mu = \theta_0 = 0$과 $\phi_\mu = \phi_0 = 0$에서 다음이 만족된다.
\[\begin{equation} \frac{\partial \epsilon}{\partial \theta_\mu} (0, 0) = 0, \quad \frac{\partial \epsilon}{\partial \phi_\mu} (0, 0) = 0 \end{equation}\]그러므로 $(0, 0)$은 오차 함수의 극점이며, 저자들이 확인한 결과 이 점은 최소점이다.
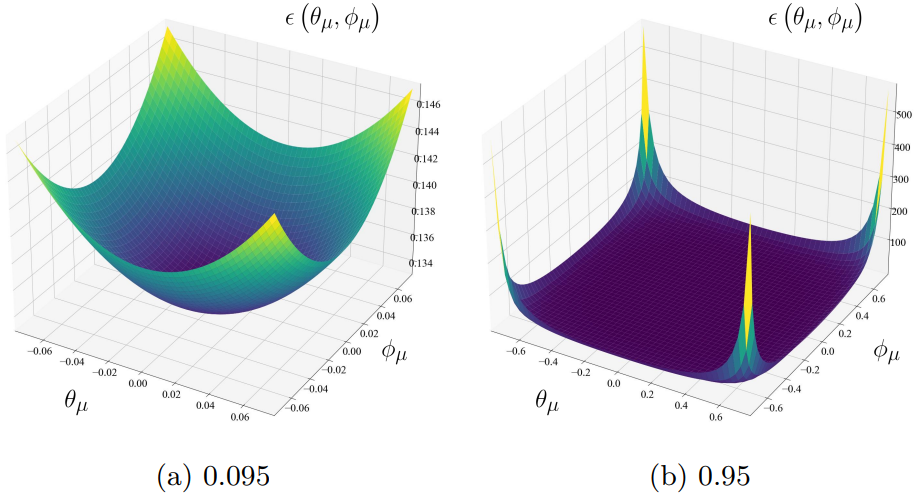
위 그림은 오차 함수를 시각화한 것이다. (a)를 보면 오차 함수는 오목 함수이며 $(0, 0)$에서 최소값을 얻는다. (b)를 보면 원점에 가까운 대부분의 영역에서 함수 값이 크게 다르지 않다. 그러나 함수가 적분 한계에 가까워 지면 함수값이 급격히 증가하여 최대값과 최소값 사이에 상당한 차이가 발생한다.
즉, 대부분의 경우 오차가 작아서 렌더링된 이미지의 품질에 큰 영향을 미치지 않는다. 이것이 3D-GS가 local affine approximation을 활용하면서도 고품질의 새로운 뷰 이미지를 얻고 장면을 성공적으로 재구성하는 이유이다. 그럼에도 불구하고 3D-GS에서 모든 Gaussian을 동일한 평면 $z = 1$로 projection하면 중심에서 더 멀리 있는 Gaussian에 대해 더 큰 projection 오차가 발생하여 아티팩트가 발생할 수 있다.
Optimal Gaussian Splatting
본 논문은 오차 함수의 분석을 바탕으로 projection 오차가 더 작아서 더 높은 품질의 렌더링을 제공하는 Optimal Gaussian Splatting을 도입하였다.
1. Optimal Projection
저자들은 오류 함수의 분석을 통해 평면에 대한 Gaussian 평균의 projection이 카메라 중심에서 평면으로의 projection과 일치할 때 오차 함수가 최소값에 도달한다는 것을 발견했다. 따라서 Optimal Gaussian Splatting에서는 Optimal Projection을 사용한다. 특히, 서로 다른 Gaussian을 동일한 평면 $z = 1$에 단순하게 projection하는 대신 각 Gaussian에 대해 별도의 projection 평면을 채택한다. 이러한 projection 평면은 Gaussian 평균과 이를 카메라 중심에 연결하는 선에 의해 형성된 접평면에 의해 결정된다. 특정 projection 평면은 다음과 같이 공식화된다.
\[\begin{equation} \textbf{x}^{\mu \top} \cdot (\textbf{x}^\prime - \textbf{x}^\mu) = 0 \\ \textrm{where} \quad \textbf{x}^\mu = \pi (\boldsymbol{\mu}^\prime) = \boldsymbol{\mu}^\prime (\boldsymbol{\mu}^{\prime \top} \boldsymbol{\mu}^\prime)^{-1/2} \end{equation}\]$\textbf{x}^\mu$는 이 평면에 대한 카메라 좌표계 원점의 projection을 나타낸다. Projection 평면 방정식에 따르면 Optimal Projection 함수 $\phi_o$는 다음과 같이 구해진다.
\[\begin{aligned} \phi^\mu (\textbf{x}^\prime) &= \textbf{x}^\prime (\textbf{x}^{\mu \top} \textbf{x}^\prime)^{-1} (\textbf{x}^{\mu \top} \textbf{x}^\mu) \\ &= (\textbf{x}^{\mu \top} \textbf{x}^\prime)^{-1} \end{aligned}\]대응되는 local affine approximation의 Jacobian matrix \(\textbf{J}_o\)는 다음과 같다.
\[\begin{aligned} \textbf{J}^\mu &= \frac{\partial \phi^\mu}{\partial \textbf{x}^\prime} (\boldsymbol{\mu}^\prime) \\ &= \mathbb{I} \otimes (\textbf{x}^{\mu \top} \boldsymbol{\mu}^\prime)^{-1} - \textbf{x}^\mu (\textbf{x}^{\mu \top} \boldsymbol{\mu}^\prime)^{-1} (\boldsymbol{\mu}^{\prime \top} \textbf{x}^\mu)^{-1} \boldsymbol{\mu}^{\prime \top} \end{aligned}\]$\boldsymbol{\mu}^\prime = [\mu_x, \mu_y, \mu_z]^\top$일 때, Jacobian matrix는 다음과 같다.
\[\begin{equation} \textbf{J}^\mu = \frac{1}{(\mu_x^2 + \mu_y^2 + \mu_z^2)^{3/2}} \begin{bmatrix} \mu_y^2 + \mu_z^2 & - \mu_x \mu_y & - \mu_x \mu_z \\ - \mu_x \mu_y & \mu_x^2 + \mu_z^2 & - \mu_y \mu_z \\ - \mu_x \mu_z & - \mu_y \mu_z & \mu_x^2 + \mu_y^2 \end{bmatrix} \end{equation}\]2. Unit Sphere Based Rasterizer
Optimal Projection의 경우, 이미지 생성을 위한 rasterization을 위해 Unit Sphere Based Rasterizer를 채택하였다.
Optimal Projection을 통해 이미지 공간에서 Gaussian을 얻는 대신 단위 구의 접평면에 3D Gaussian을 projection한다. 따라서 이미지를 생성하기 위해서는 이 단위 구를 기반으로 rasterization을 해야 한다.
구체적으로, NeRF와 유사하게 이미지의 픽셀 $(u, v)$에 대해 광선을 투사한다. 그러나 NeRF와 달리 광선을 따라 점을 광범위하게 샘플링하지 않고, 대신 광선이 단위 구에서 어떤 접평면 Gaussian과 교차하는지 결정하는 데만 초점이 있으므로 성능이 크게 저하되지 않는다.
\[\begin{equation} \textbf{x}_\textrm{2D}^\mu = \phi^\mu \bigg( \begin{bmatrix} (u - c_x) / f_x \\ (v - c_y) / f_y \\ 1 \end{bmatrix} \bigg) \end{equation}\]그런 다음 색상을 얻기 위한 알파 블렌딩을 위해 Gaussian의 함수값을 쿼리한다.
\[\begin{equation} G_\textrm{2D}^\mu (\textbf{x}_\textrm{2D}^\mu) = \exp (-1/2 (\textbf{x}_\textrm{2D}^\mu - \phi (\boldsymbol{\mu}^\prime))^\top (\textbf{J}^\mu \boldsymbol{\Sigma}^\prime \textbf{J}^{\mu \top})^{-1} (\textbf{x}_\textrm{2D}^\mu - \phi (\boldsymbol{\mu}^\prime))) \\ \alpha (u, v, \boldsymbol{\mu}) = \alpha_{\boldsymbol{\mu}} \cdot G_\textrm{2D}^\mu (\textbf{x}_\textrm{2D}^\mu) \\ \textbf{C} (u, v) = \sum_{z = z_\textrm{near}}^{z_\textrm{far}} \textrm{SH} (\boldsymbol{\mu}_z) \alpha (u, v, \boldsymbol{\mu}_z) \prod_{k = z_\textrm{near}}^z (1 - \alpha (u, v, \boldsymbol{\mu}_k)) \end{equation}\]여기서 $z_\textrm{near}$에서 $z_\textrm{far}$까지의 합과 곱은 광선이 만나는 3D Gaussian의 깊이에 대해 가까운 곳에서 먼 곳으로 오름차순으로 정렬된 이산화된 깊이를 나타내고, $\alpha_{\boldsymbol{\mu}}$는 평균이 $\boldsymbol{\mu}$인 3D Gaussian의 투명도, \(\boldsymbol{\mu}_z\)는 깊이가 $z$인 Gaussian의 평균, SH는 이 Gaussian의 spherical harmonics이다.
$\textbf{J}^\mu$와 $\textbf{J}$는 모두 rank가 2인 행렬이다. 따라서 실제로 $\textbf{J}^\mu \boldsymbol{\Sigma}^\prime \textbf{J}^{\mu \top}$에는 역행렬이 없다. 세 번째 행을 0으로 만들기 위해 $\textbf{J}^\mu$에 대해 가역 변환을 수행한다. 결과적으로 $\textbf{J}^\mu \boldsymbol{\Sigma}^\prime \textbf{J}^{\mu \top}$는 세 번째 행과 세 번째 열이 모두 0인 행렬이 된다. 이를 통해 세 번째 행과 세 번째 열을 건너뛰고 $\textbf{J}$와 유사하게 마치 2$\times$2 행렬인 것처럼 역행렬을 계산할 수 있다. 식이 계속 만족하도록 하려면 이 역행렬을 \(\textbf{x}_\textrm{2D}^\mu\)와 $\phi (\boldsymbol{\mu}^\prime)$의 left multiplication에도 사용해야 한다.
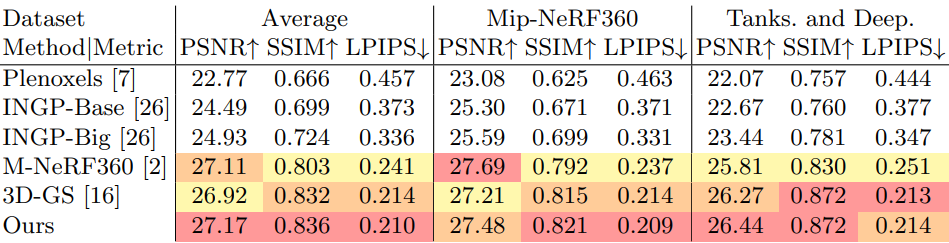
Experiments
다음은 여러 데이터셋에서 다른 방법들과 비교한 결과이다.