[논문리뷰] OpenGaussian: Towards Point-Level 3D Gaussian-based Open Vocabulary Understanding
NeurIPS 2024. [Paper] [Page] [Github]
Yanmin Wu, Jiarui Meng, Haijie Li, Chenming Wu, Yahao Shi, Xinhua Cheng, Chen Zhao, Haocheng Feng, Errui Ding, Jingdong Wang, Jian Zhang
Peking University | Baidu VIS | Beihang University
4 Jun 2024
Introduction
학습 가능한 언어 속성을 3DGS에 통합하여 3DGS를 언어 기반 능력으로 향상시키려는 여러 방법들이 있었다. 이러한 방법들의 주요 목표는 2D 픽셀 수준 이해를 위해 언어 속성을 이미지에 렌더링하고 2D feature를 3D로 끌어올리는 것이다. 이러한 방법은 가려진 물체 또는 부분을 인식할 수 없어 3DGS의 고유한 3D 능력이 손상되며, 3D 포인트 수준 이해, 위치 파악, 상호 작용이 필요한 애플리케이션과 호환되지 않는다. 따라서 본 논문은 3DGS에 3D 포인트 수준의 open-vocabulary 기능을 제공하는 것을 목표로 한다.
기존 방법들은 대상 물체를 효과적으로 매칭하는 데 있어 어려움이 있으며, 2D 이미지에서는 강력한 성능을 보이지만 3D 이해 능력에는 제한이 있다. 이러한 제한은 두 가지 주요 요인에 기인한다.
- 약한 feature 표현력: 3DGS에서 3D Gaussian별 학습 및 렌더링과 관련된 메모리 및 속도 제약으로 인해 장면에서 수백만 개의 Gaussian에 대한 고차원 language feature를 학습하는 것이 어려워진다. 결과적으로 기존 방법은 차원을 줄이기 위해 distillation 또는 quantization과 같은 차원 축소 기법에 의존한다. 그러나 이는 필연적으로 feature의 표현력과 구별성을 저해한다.
- 부정확한 2D-3D 대응: 알파 블렌딩 렌더링 기법은 불투명도 가중치를 기반으로 3D 포인트의 값을 누적하여 2D 픽셀을 렌더링하므로, 2D와 3D 간의 일대일 대응이 이루어지지 않는다. 결과적으로 2D와 3D 해석 간에 성능 불일치가 발생한다.
이러한 과제를 해결하기 위해, 본 논문에서는 물체 간 및 물체 내부 모두에서 3D 포인트 수준에서 독특하고 일관된 feature를 학습하는 접근법인 OpenGaussian을 제안하였다. OpenGaussian은 고차원 무손실 CLIP feature를 3D Gaussian 포인트와 연관시켜 open-vocabulary 3D 장면 이해를 가능하게 한다.
구체적으로, 제안된 intra-mask smoothing loss와 inter-mask contrastive loss를 사용하여 구별적이고 3D 일관성을 유지하는 3D 포인트 수준 인스턴스 feature를 학습시키고, 프레임 간 연관 없이 SAM의 바이너리 마스크를 활용한다. 인스턴스 feature를 discretize하기 위해 2단계의 coarse-to-fine codebook을 도입하여 discrete한 3D 인스턴스 클러스터를 생성한다. 또한, 각 3D 인스턴스에 대해 여러 뷰의 CLIP feature를 연관시키기 위해 IoU와 feature 거리 기반 인스턴스 레벨 2D-3D 연관 방법을 제안하였다.
OpenGaussian은 기존 CLIP feature의 open-vocabulary 능력을 그대로 유지하면서 feature 차원 압축이나 quantization을 위한 추가 네트워크의 필요성을 제거한다.
Method

1. 3D Consistency-Preserving Instance Feature Learning
3DGS는 3D Gaussian을 명시적 장면 표현으로 활용한다. 각 Gaussian은 위치 $\boldsymbol{\mu}$, rotation $\textbf{R}$, scale $\textbf{S}$, 불투명도 $\sigma$, 방향에 따른 색상 $\textbf{c}$를 나타내는 spherical harmonics 계수와 같은 다양한 속성을 포함한다. 3D Gaussian 집합이 2D 화면 공간에 projection되고 블렌딩되어 픽셀을 생성한다.
각 3D Gaussian을 저차원 feature $\textbf{f} \in \mathbb{R}^6$로 확장하여 인스턴스 속성을 나타낸다. 본 논문의 방식은 두 가지 중요한 측면에서 다른 방법들과 다르다.
- 이전 방법들에서 널리 사용된 사전 학습된 feature에 대해 추가적인 차원 감소, quantization, distillation이 필요하지 않다.
- 장면 내 객체 개수 계산을 위해 추적 기반 2D 방법에 의존하는 대신, 3D Gaussian의 멀티뷰 글로벌 일관성을 활용하여 instance feature를 제한한다.
동일한 물체의 렌더링된 feature는 서로 가까워야 하고, 다른 물체의 렌더링된 feature는 서로 떨어져 있어야 한다는 원칙을 고수한다. 이를 위해, 시점 사이의 상관관계가 없는 바이너리 SAM 마스크를 사용하여 instance feature를 학습시킨다.
임의의 학습 뷰가 주어지면, splatting 과정을 따라 3D instance feature $\textbf{f}$를 알파 블렌딩을 통해 feature map $\textbf{M} \in \mathbb{R}^{6 \times H \times W}$로 렌더링한다. $i$번째 SAM 마스크 \(\textbf{B}_i \in \{0, 1\}^{1 \times H \times W}\)가 주어지면, 마스크 내 평균 feature를 다음과 같이 구할 수 있다.
\[\begin{equation} \bar{\textbf{M}}_i = \frac{\textbf{B}_i \cdot \textbf{M}}{\sum \textbf{B}_i} \in \mathbb{R}^6 \end{equation}\]각 마스크 내 feature가 평균에 가깝도록 하기 위해 intra-mask smoothing loss를 도입한다.
\[\begin{equation} \mathcal{L}_s = \sum_{i=1}^m \sum_{h=1}^H \sum_{w=1}^W \textbf{B}_{i,j,w} \cdot \| \textbf{M}_{:,h,w} - \bar{\textbf{M}}_i \|^2 \end{equation}\]($H$와 $W$는 각각 이미지의 높이와 너비, $m$은 현재 뷰의 SAM 마스크 개수)
또한, 다양한 인스턴스 간의 feature 다양성을 높이기 위해 마스크 간 평균 feature 거리를 증가시킨다. 이를 inter-mask contrastive loss라고 하며, 다음과 같이 정의된다.
\[\begin{equation} \mathcal{L}_c = \frac{1}{m (m-1)} \sum_{i=1}^m \sum_{j=1, j \ne i}^m \frac{1}{\| \bar{\textbf{M}}_i - \bar{\textbf{M}}_j \|^2} \end{equation}\]이러한 전략을 활용하여 마스크에서 직접 유의미한 3D cross-view 일관성과 고유한 instance feature를 성공적으로 얻을 수 있으며, 시점 사이의 상관관계가 필요 없다.
2. Two-Level Codebook for Discretization
직관적으로 학습된 instance feature는 상호작용적인 3D segmentation에 매우 적합한 것으로 보인다. 예를 들어, 렌더링된 feature map 내의 픽셀을 클릭하면 유사한 feature를 가진 Gaussian을 검색하여 선택된 물체를 식별할 수 있다. 그러나 이 접근법의 실제 구현에는 다음과 같은 어려움이 있다.
- 유사한 feature를 선택하기 위한 보편적인 threshold를 설정하는 것이 어렵다.
- Feature map은 가중치를 누적하는 알파 블렌딩을 사용하여 렌더링되므로, 동일한 물체의 Gaussian이 서로 다른 feature를 보이거나, 서로 다른 물체의 Gaussian이 유사한 feature를 공유할 수 있다.
Instance feature의 고유성을 높이고 상호작용성을 향상시키기 위해, 동일한 인스턴스의 Gaussian을 discrete하여 단순히 유사한 것이 아닌 동일한 feature를 갖도록 한다. 이를 위해 저자들은 codebook discretization을 도입하였다.
Codebook for Discretization
모든 $n$개의 Gaussian에 대한 instance feature $\textbf{F} \in \mathbb{R}^{n \times 6}$이 주어지면, 먼저 $\textbf{F}$에서 $k = 64$개의 feature를 무작위로 선택하여 quantization codebook $\textbf{C} \in \mathbb{R}^{k \times 6}$을 초기화한다.
1) 각 instance feature \(\{\textbf{f}_i\}_{i=1}^n\)에 대해 codebook $\textbf{C}$에서 가장 가까운 quantized feature \(\{\textbf{c}_j\}_{j=1}^k\)를 찾고 각 Gaussian의 quantization 인덱스 $j$를 $\textbf{I} \in \mathbb{R}^{n \times 1}$에 저장한다. 2) Feature map 렌더링 및 loss 계산 시에 \(\textbf{c}_j\)는 \(\textbf{f}_i\)를 대체한다. 3) Backpropagation 동안, quantized feature의 gradient는 instance feature로 복사된다. 따라서 instance feature $f_i$가 최적화된다. 4) 이후, codebook $\textbf{C}$는 인덱스 $\textbf{I}$와 $\textbf{F}$를 기반으로 업데이트된다.
위의 1)부터 4)까지의 단계를 반복한다. 마지막으로, instance feature $\textbf{F}$를 quantized feature와 인덱스 \(\{\textbf{C}, \textbf{I}\}\)로 변환하여 장면 내 인스턴스를 discretize한다.
그러나 이 해결책은 여전히 다음과 같은 과제를 안고 있다.
- 가려짐이나 거리로 인해 두 물체가 동일한 시점을 공유하지 못할 수 있으며, 이로 인해 contrastive loss로 최적화되지 않아 두 물체의 feature가 서로 구별되지 않는다.
- 대규모 시나리오에서 $k$ 값 64는 모든 물체를 구별하기에 충분하지 않아 instance feature의 고유성이 감소한다. 그러나 단순히 $k$ 값을 높이는 것만으로는 성능이 향상되지 않는다.
Two-Level Codebook
저자들은 위의 문제들을 해결하기 위해 두 단계의 coarse-to-fine codebook discretization을 제안하였다. 먼저, codebook을 생성하기 위해 instance feature $\textbf{F}$를 Gaussian의 3D 좌표 $\textbf{X} \in \mathbb{R}^{n \times 3}$과 연결하여 위치 의존적 클러스터링을 구현한다. 이후, instance feature만을 기반으로 각 coarse 클러스터 내에서 추가로 discrete한다. 따라서 이 접근법은 멀리 떨어져 있고 서로 보이지 않는 물체들이 같은 클러스터에 할당되는 문제를 방지할 뿐만 아니라, 큰 장면을 분할하여 최적화의 복잡성을 줄인다.
\[\begin{aligned} \left[ \textbf{F} \in \mathbb{R}^{n \times 6}; \textbf{X} \in \mathbb{R}^{n \times 3} \right] &\mapsto \{\textbf{C}_\textrm{coarse} \in \mathbb{R}^{k_1 \times (6+3)}, \textbf{I}_\textrm{coarse} \in \{1, \ldots, k_1\}^n \} \\ \textbf{F} \in \mathbb{R}^{n \times 6} &\mapsto \{\textbf{C}_\textrm{fine} \in \mathbb{R}^{(k_1 \times k_2) \times 6}, \textbf{I}_\textrm{fine} \in \{1, \ldots, k_2\}^n \} \end{aligned}\]이를 통해, instance feature $\textbf{F}$가 2단계 codebook \(\{\textbf{C}, \textbf{I}\}_\textrm{coarse}\), \(\{\textbf{C}, \textbf{I}\}_\textrm{fine}\)으로 discretize된다. 특히, coarse 단계에서 Gaussian의 위치는 codebook 생성에만 사용되고 최적화에는 관여하지 않으므로 사전 학습된 Gaussian 모델의 기하학적 구조가 유지된다.
Pseudo Feature Loss
Instance feature 학습 단계에서 supervision은 바이너리 SAM 마스크로 제한된다. 그러나 현재 codebook 구축 단계에서는 더욱 강력한 supervision을 제공하는 고유한 instance feature들을 얻었다. 따라서 이전의 마스크 loss를 대체하고 첫 번째 단계의 instance feature를 pseudo GT로 복제할 수 있다.
\[\begin{equation} \mathcal{L}_p = \| \textbf{M}_p - \textbf{M}_c \|^1 \end{equation}\](\(\textbf{M}_p \in \mathbb{R}^{6 \times H \times W}\)는 1단계 pseudo feature에서 렌더링된 feature map, \(\textbf{M}_c \in \mathbb{R}^{6 \times H \times W}\)는 quantized feature에서 렌더링된 feature map)
3. Instance-Level 2D-3D Association without Depth Test
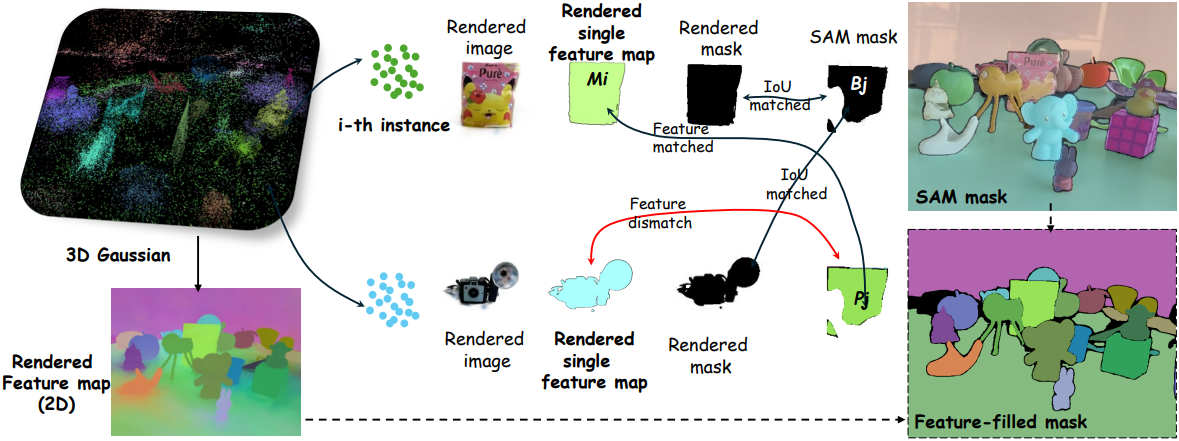
위에서 설명한 codebook discretization 프로세스를 통해 클릭과 같은 프롬프트로 3D 물체를 선택하는 능력이 향상된다. 보다 자연스럽고 open-vocabulary 기반 상호작용을 더욱 활성화하려면 3D Gaussian을 language feature와 효과적으로 연관시키는 것이 필수적이다.
저자들은 깊이 기반 occlusion 테스트의 필요성을 피하면서 고차원의 무손실 language feature를 유지하는 효율적인 인스턴스 레벨 3D-2D 연관 방법을 제안하였다. 구체적으로, 먼저 단일 3D 인스턴스의 feature를 현재 뷰에 렌더링하여 single-instance map \(\textbf{M}_i \in \mathbb{R}^{6 \times H \times W}\)로 렌더링한 다음 ($i \in [1, \ldots, k_1 \cdot k_2$]), 현재 뷰의 SAM 마스크 \(\textbf{B}_j \in \{0, 1\}^{1 \times H \times W}\)와 IoU를 계산한다 ($j$는 마스크 인덱스). 직관적으로, 가장 높은 IoU를 갖는 SAM 마스크가 이 3D 인스턴스와 연관된다.
그러나 occlusion으로 인해 하나의 SAM 마스크가 여러 3D 인스턴스에서 렌더링된 single-instance map과 교차할 수 있다. 따라서 바이너리 SAM 마스크 \(\textbf{B}_j\)에 pseudo GT feature를 채워 feature-filled mask \(\textbf{P}_j \in \mathbb{R}^{6 \times H \times W}\)를 만든 다음, \(\textbf{P}_j\)와 \(\textbf{M}_j\) 사이의 feature 거리를 계산하여 IoU가 높지만 feature가 동일한 물체에 해당하지 않는 상황을 방지한다.
\[\begin{equation} \mathcal{S}_{ij} = \textrm{IoU} (\pi (\textbf{M}_i), \textbf{B}_j) \cdot (1 - \| \textbf{M}_i - \textbf{P}_j \|^1) \end{equation}\]($\pi (\cdot)$은 binarization 연산)
\(\mathcal{S}_{ij}\)는 현재 뷰에서 $i$번째 3D 인스턴스와 $j$번째 SAM 마스크 간의 점수를 나타낸다. 첫 번째 항은 IoU를 계산하며, 두 번째 항의 값은 feature 거리에 반비례한다. 마지막으로, 가장 높은 점수를 가진 마스크의 CLIP 이미지 feature들은 3D 인스턴스의 Gaussian과 연관되며, 멀티뷰 feature들의 통합 또한 고려된다.
Experiments
1. Open-Vocabulary Object Selection in 3D Space
다음은 LERF 데이터셋에서의 open-vocabulary 3D object selection 성능을 비교한 결과이다.


2. Open-Vocabulary Point Cloud Understanding
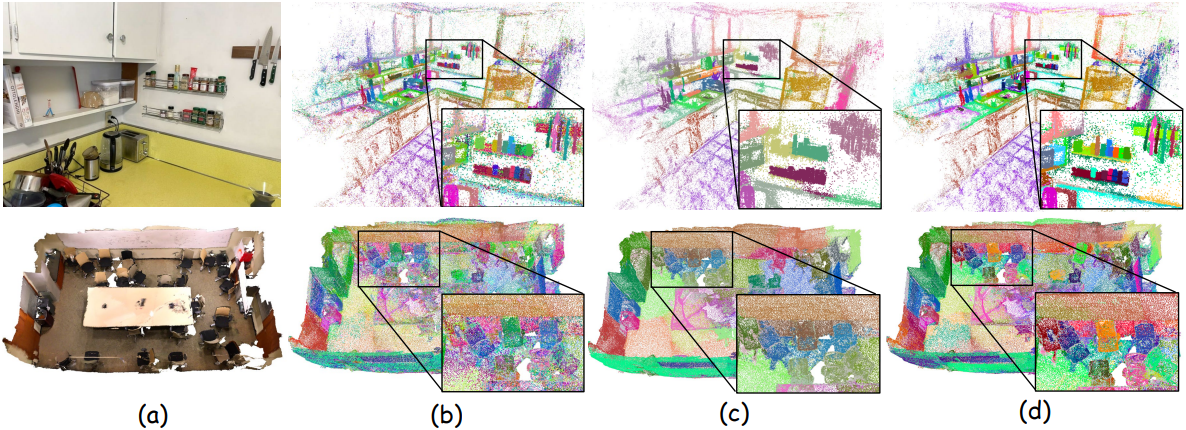
다음은 3D feature를 시각화하여 비교한 결과이다.

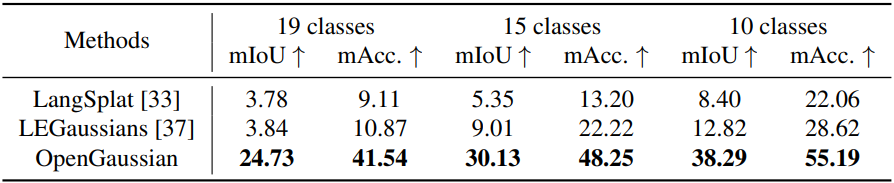
다음은 Scannet 데이터셋에서의 semantic segmentation 성능을 비교한 결과이다.
3. Click-based 3D Object Selection
다음은 클릭 기반 object selection 결과를 비교한 것이다.

4. Ablation Study
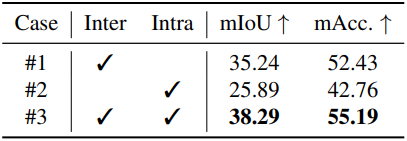
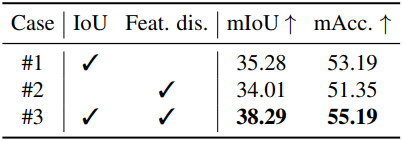
다음은 (왼쪽) inter/intra loss와 (오른쪽) 2D-3D 연관 전략에 대한 ablation 결과이다.
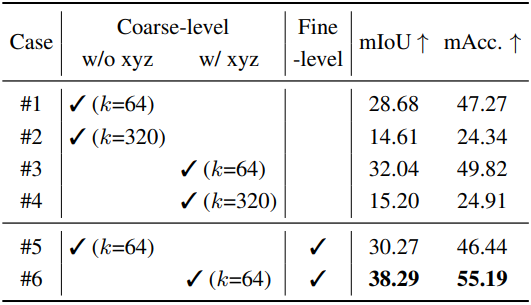
다음은 다양한 codebook 구성에 대한 semantic segmentation 성능을 비교한 결과이다.
Limitations
- Gaussian의 기하학적 속성은 고정되어 있기 때문에, 기하학적 표현과 semantic 간의 불일치로 이어질 수 있다.
- 2단계 codebook의 $k$ 값은 경험적으로 결정된다.
- 물체 크기를 고려하지 않고 3D 포인트 수준의 이해에 집중한다.
- 동적 요소를 고려하지 않는다.