[논문리뷰] Conditional Latent Diffusion Models for Zero-Shot Instance Segmentation

ICCV 2025. [Paper]
Maximilian Ulmer, Wout Boerdijk, Rudolph Triebel, Maximilian Durner
German Aerospace Center | Karlsruhe Institute of Technology | Technical University of Munich
6 Aug 2025

Introduction

본 논문은 inference 과정에서 컨디셔닝 정보만 요구하면서 임의의 object에 대한 클래스별 인스턴스 예측을 생성하는 Zero-Shot Instance Segmentation (ZSI)을 목표로 한다. 따라서 기존 방법들과 달리 CAD 모델별 학습 없이 인스턴스별 예측을 유지한다. 일반적으로 ZSI 방식은 test-time에 관련 object 모델을 기반으로 렌더링된 템플릿 이미지의 feature 표현을 생성한다. 이후, 이 feature 표현을 실제 이미지 feature와 비교하여 쿼리 이미지에서 관심 object를 검색한다. 시뮬레이션 이미지와 실제 이미지 간의 차이 외에도, 제한된 템플릿의 양은 대상 object의 다양한 스케일에서 변화하는 외형을 분석하는 데 제약을 준다.

최근 논문들은 ZSI를 두 단계로, 즉 영역을 추출하고 이를 템플릿 feature와 비교하는 방식으로 접근한다. 이와 대조적으로, 본 논문에서는 object 가설 생성과 feature 매칭을 end-to-end 방식으로 통합하는 Object-Conditioned Diffusion Transformer (OC-DiT)를 도입하였다. 본 논문에서 제안하는 diffusion 기반 접근법은 생성 프로세스를 통해 개별 인스턴스를 분리하고, latent space에서 템플릿 feature와 이미지 feature를 매칭한다.

Method

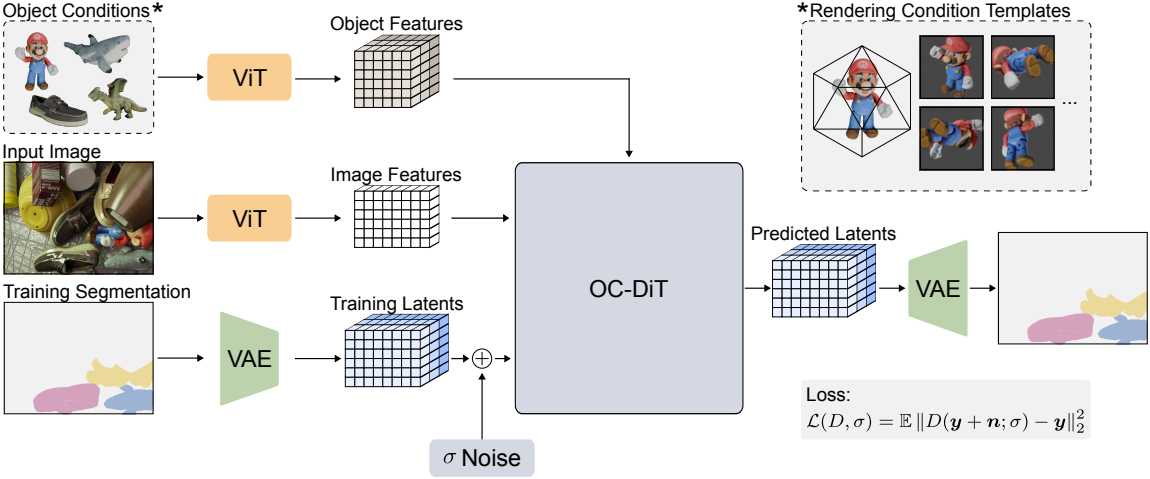
본 논문에서는 DiT에서 영감을 받아 RGB 이미지 생성을 위해 설계된 Object-Conditioned Diffusion Transformer (OC-DiT)를 도입하였다. Timestep과 클래스 레이블에 대한 컨디셔닝은 지원하지만, object feature와 같은 대규모 컨디셔닝은 지원하지 않는다.

입력 이미지 $\textbf{I} \in \mathbb{R}^{H \times W \times 3}$와 대상 object 집합 \(\mathcal{O} = \{o_1, \ldots, o_{N_\mathcal{O}}\}\)의 쌍 $\textbf{c} = (\textbf{I}, \mathcal{O})$가 주어졌을 때, 본 논문은 instance segmentation을 조건부 생성 프로세스로 가정하였다. 목표는 조건부 분포 $p(\textbf{x} \vert \textbf{c})$를 샘플링하는 것이다. Inference 단계에서는 분포 \(p(\textbf{x} \vert \textbf{c}; \sigma_\textrm{max})\)를 \(p(\textbf{x} \vert \textbf{c}; \sigma = 0)\)으로 진화시켜 대상 object $\mathcal{O}$를 분할하도록 $\textbf{x}$의 결과를 컨디셔닝한다. 이를 위해 조건부 입력을 입력받는 denoising 네트워크 \(D_\theta (\textbf{x}; σ, \textbf{c})\)를 학습킨다.

저자들은 입력 해상도 $H \times W$, object 개수 \(N_\mathcal{O}\), object당 템플릿 개수 \(N_\mathcal{T}\)에 대한 유연성을 고려하여 OC-DiT를 설계하였다. 따라서 패치 기반 시퀀스 처리 방식을 사용하는 ViT를 기반으로 하는 DiT를 채택하였다.

Latent Diffusion of Bernoulli Distributions

Binary segmentation mask의 분포를 직접 샘플링할 수 있다. 그러나 diffusion model은 \(\mu_\textrm{data} = 0\)이고 \(\sigma_\textrm{data} = 0.5\)인 정규 분포를 따르는 RGB 이미지를 고려한다. 이러한 요구 사항은 베르누이 분포를 따르는 binary segmentation과 크게 다르다. Forward process에서 바이너리 데이터에 Gaussian noise를 더해도 정규 분포를 갖는 학습 데이터 \(p_\textrm{data}\)가 생성되지 않는다.

이 문제를 해결하기 위해, 저자들은 $\beta$-VAE를 사용하여 마스크를 저차원 latent space로 압축하고 latent diffusion을 수행한다. VAE를 사용하면 학습 중에 latent space 통계를 요구 사항에 맞게 조정할 수 있다. 또한, 차원 감소는 계산 효율을 크게 향상시킨다.

Latent code \(\textbf{x} \in \mathbb{R}^{h \times w \times d}\)는 인코더 \(V_\textrm{enc}\)에 의해 바이너리 이미지 \(\textbf{b} \in \{0, 1\}^{H \times W}\)에서 생성된다. 인코딩 프로세스는 이미지를 $H/h$배로 다운샘플링한다. 반대로, 디코더 \(V_\textrm{dec}\)는 각 픽셀 위치에 대해 신뢰도 맵 \(\tilde{b} \in [0, 1]^{H \times W}\)를 재구성한다.

\[\begin{aligned} \textbf{x} &= V_\textrm{enc} (\textbf{b}) \\ \tilde{\textbf{b}} &= V_\textrm{dec} (V_\textrm{enc} (\textbf{b})) \end{aligned}\]

VAE를 사용하면 diffusion process는 latent space에서만 이루어진다. 학습 과정에서 \(V_\textrm{enc}\)는 바이너리 마스크 $\textbf{b}​$로부터 latent code $\textbf{x}$를 생성하고, 이 latent code들은 noise로 손상된다. 원래 latent code를 복구하도록 denoiser \(D_\theta\)를 학습시키므로, 학습 과정에서 \(V_\textrm{dec}\)는 필요하지 않다. 반대로, inference 과정에서는 순수한 noise가 $N$ step에 걸쳐 \(D_\theta\)에 의해 반복적으로 denoising된다. \(V_\textrm{dec}\)는 최종적으로 noise가 제거된 latent code \(\textbf{x}_0\)에만 적용되며, \(V_\textrm{enc}\)는 필요하지 않다.

Query Embeddings

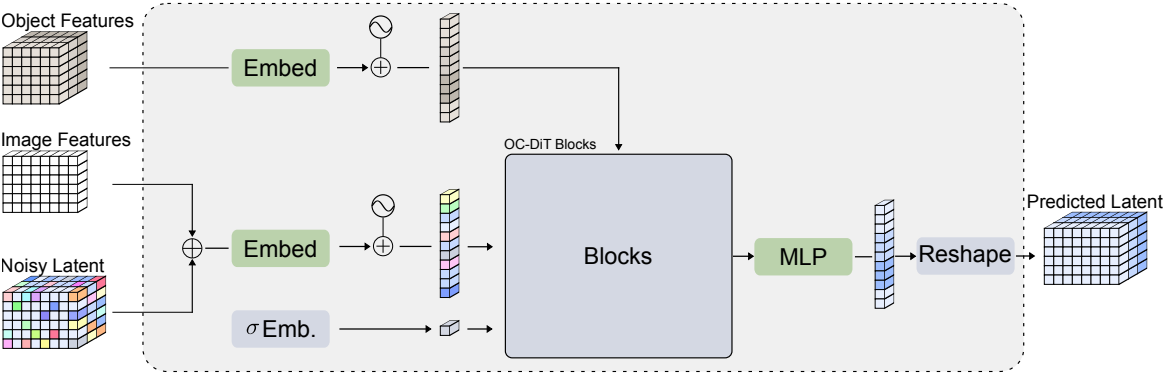
분할하려는 각 대상 object에 대해 하나의 쿼리 $\textbf{q}$를 생성한다. 각 쿼리는 사전 학습된 backbone \(f_\textbf{I}\)의 feature와 concat된 latent code로 구성된다. 학습 단계에서는 GT latent \(\textbf{x} = V_\textrm{enc} (\textbf{b})\)가 noise에 의해 손상된다.

\[\begin{equation} \textbf{y} = \textbf{x} + \textbf{n}, \quad \textbf{n} \sim \mathcal{N}(0, \sigma^2 I) \end{equation}\]

그러나 inference 단계에서는 이전 timestep \(\textbf{x}_{i-1}\)에서 예측된 latent code가 사용된다.

Concat 후, convolutional layer는 원래 ViT와 마찬가지로 각 쿼리를 차원 $d_e$의 임베딩 공간에 임베딩한다. 공간 차원을 따라 쿼리를 $n_q = h \cdot w$로 flatten한 후, 모든 object에 대해 쿼리 토큰

\[\begin{equation} \tau^q = [\tau_0^q, \ldots, \tau_{N_\mathcal{O}}^q] \in \mathbb{R}^{N_\mathcal{O} \times n_q \times d_e} \end{equation}\]

을 얻는다. DiT의 주파수 기반 위치 인코딩 대신, 2D 패치와 1D object 위치에 대해 학습된 인코딩을 사용한다.

Conditioning Objects Template Embeddings

본 논문의 목표는 object 집합 $\mathcal{O}$에 대한 diffusion process를 컨디셔닝하는 것이다. 각 object에 대한 \(N_\mathcal{T}\)개의 템플릿 집합 \(\mathcal{T}_j\)를 렌더링하여 전체 템플릿 집합 \(\mathcal{T} = \{\mathcal{T}_1, \ldots, \mathcal{T}_{N_\mathcal{O}}\}\)를 생성한다.

사전 학습된 ViT를 사용하여 각 템플릿에 대한 feature를 추출하여 모델의 패치 크기와 임베딩 차원에 의해 공간적으로 정의된 저차원 feature 공간을 생성한다. 다음으로, convolutional layer는 각 템플릿을 임베딩한 후, 템플릿당 \(n_\mathcal{T} = h_\mathcal{T} \times w_\mathcal{T}\)개의 토큰으로 flatten하여 \(\tau_\mathcal{T} \in \mathbb{R}^{N_\mathcal{O} \times N_\mathcal{T} \times n_\mathcal{T} \times d_e}\)이 되도록 한다. 마지막으로, 학습된 위치 인코딩을 템플릿에 적용하여 2D 패치 위치, 1D object 위치, 1D 템플릿 위치를 인코딩한다.

Noise Embeddings

저자들은 EDM2를 따라 diffusion process의 timestep이 아닌 현재 noise level \(c_\textrm{noise}(\sigma)\)의 로그 값을 기준으로 네트워크를 컨디셔닝하였다. Magnitude-preserving Fourier feature를 사용하여 linear layer와 SiLU layer를 통과하기 전에 값을 임베딩 차원에 임베딩한다.

OC-DiT Decoder

임베딩 후, 일련의 transformer block이 쿼리 토큰 \(\tau^q\)를 처리한다. 각 block은 세 개의 layer, 즉 cross-attention layer, self-attention layer, MLP로 구성된다. 중요한 것은 cross-attention 단계에서 쿼리 토큰을 재배열하여 각 쿼리가 할당된 object의 템플릿 토큰에만 attention하도록 한다는 것이다. Cross-attention layer 후, 각 쿼리 토큰이 self-attention 동안 다른 모든 쿼리 토큰에 attention하도록 쿼리 토큰을 reshape한다. 이를 통해 cross-attention 단계의 계산 비용을 크게 줄이고 모델이 각 쿼리가 하나의 object에 매칭된다는 것을 학습하는 데 중요하다.

DiT와 유사하게 self-attention과 MLP에서 adaLN을 사용하며, 추가로 저자들은 cross-attention 부분에 세 번째 adaLN을 추가하였다. adaLN은 noise level에 토큰을 변조한다. Scale $\gamma$, shif $\beta$, gating $\alpha$ 값은 noise level을 linear layer에 통과시켜 얻으며, 가중치는 0으로 초기화된다. MLP를 거친 후, 쿼리는 다시 원래 모양으로 reshape된다. 마지막으로, transformer block들을 통과한 이후, 최종 MLP는 쿼리 토큰을 임베딩 공간에서 latent 차원으로 projection한다.

Training and Inference

학습 과정에서 이미지 $\textbf{I}$, segmentation mask $\textbf{b}$, 해당 object $\mathcal{O}$의 쌍으로 구성된 데이터 집합에서 샘플을 추출한다. 샘플에 object가 \(N_\mathcal{O}\)개 이상 있는 경우, 샘플링된 전경 포인트와의 근접성에 따라 가중치를 부여한 object를 무작위로 선택한다. 이러한 선택은 선택된 object가 서로 가까이 위치하도록 편향되어 샘플당 전경 object에 속하는 픽셀 수가 더 많아지는 효과를 낸다. 모델의 forward pass에서 각 학습 샘플에 대해 noise level \(\sigma \in [\sigma_\textrm{min}, \sigma_\textrm{max}]\)를 무작위로 샘플링한다.

Inference 단계에서는 순수한 noise로부터 instance segmentation을 생성하며, EDM의 확률적 샘플러를 사용한다. Inference 단계에서는 timestep $N$에 대한 noise \(\textbf{x}_N \sim \mathcal{N}(0, \sigma_\textrm{max}^2 I)\)을 샘플링하여 diffusion process를 시작한다. 샘플러는 각 timestep $i$에서 noise level을 증가시킨 후 ODE를 단계적으로 실행하여 \(\textbf{x}_{i-1}\)을 생성한다. 이 과정을 $N$ step 동안 반복하여 \(\textbf{x}_0\)에 도달한다.

Test-Time Ensembling

Diffusion의 확률적 특성으로 인해 초기 noise \(\textbf{x}_N\)에 따라 예측값이 다르게 나타난다. 이 특성을 활용하여 여러 inference에 걸쳐 \(\tilde{b}\)를 평균화하고, $p(\textbf{x} \vert \textbf{c})$에서 효과적으로 여러 번 샘플링한다. 선택적으로 scaling 및 translation과 같은 공간적 test-time augmentation을 추가할 수 있다. 따라서 초기 앙상블 크기 \(N_\textrm{ensemble}\)에 대해, 각 앙상블을 \(N_\textrm{aug}\) 배 증가시켜 테스트 샘플당 총 \(N_\textrm{ensemble} \times N_\textrm{aug}\) 배의 forward pass를 생성한다. 마지막으로 모든 예측을 정렬하여 최종 앙상블 예측값을 집계한다.

Experiment

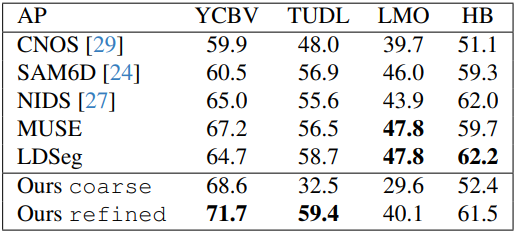
1. BOP Results

다음은 6D Object Pose Estimation 벤치마크에서의

다음은 diffusion process가 진행됨에 따른 segmentation 결과를 시각화한 것이다.

2. Increasing Conditioning Objects at test-time

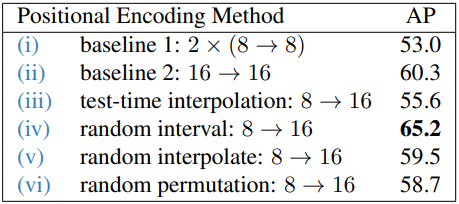
다음은 인코딩에 따른 성능을 비교한 표이다.

3. Ablations

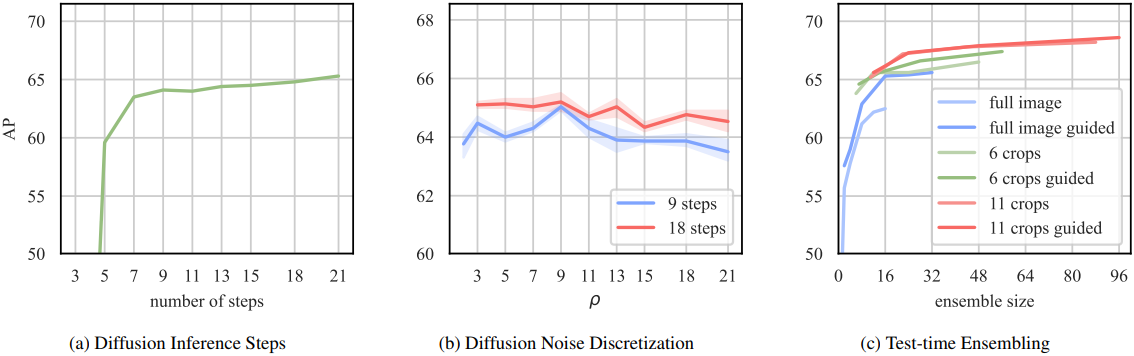
다음은 diffusion process의 다양한 측면에 대한 ablation study 결과이다.

다음은 학습 데이터셋에 대한 ablation study 결과이다.