[논문리뷰] NUWA-XL: Diffusion over Diffusion for eXtremely Long Video Generation

arXiv 2023. [Paper] [Page]
Shengming Yin, Chenfei Wu, Huan Yang, Jianfeng Wang, Xiaodong Wang, Minheng Ni, Zhengyuan Yang, Linjie Li, Shuguang Liu, Fan Yang, Jianlong Fu, Gong Ming, Lijuan Wang, Zicheng Liu, Houqiang Li, Nan Duan
University of Science and Technology of China | Microsoft Research Asia | Microsoft Azure AI
22 Mar 2023

Introduction

기존의 많은 연구들은 고화질 이미지와 짧은 동영상을 생성하는 능력을 입증했다. 그러나 실제 애플리케이션의 동영상은 종종 5초보다 훨씬 길다. 영화는 일반적으로 90분 이상 지속되고, 만화의 길이는 보통 30분이다. TikTok과 같은 “short” 동영상 애플리케이션의 경우에도 권장 동영상 길이는 21~34초이다. 매력적인 시각적 콘텐츠에 대한 수요가 계속 증가함에 따라 더 긴 동영상 생성이 점점 더 중요해지고 있다.

그러나 긴 동영상을 생성하기 위해 확장하는 것은 많은 양의 계산 리소스가 필요하기 때문에 상당한 어려움이 있다. 이 문제를 극복하기 위해 대부분의 최신 접근 방식은 “Autoregressive over X” 아키텍처를 사용한다. 여기서 “X”는 Phenaki, TATS, NUWA-Infinity와 같은 autoregressive model과 MCVD, FDM, LVDM과 같은 diffusion model을 포함하여 짧은 동영상 클립을 생성할 수 있는 모든 생성 모델을 나타낸다. 이러한 접근 방식의 기본 아이디어는 짧은 동영상 클립으로 모델을 학습시킨 다음 inference 중에 sliding window로 긴 동영상을 생성하는 데 사용한다. “Autoregressive over X” 아키텍처는 계산 부담을 크게 줄일 뿐만 아니라 학습에 짧은 동영상만 필요하므로 긴 동영상에 대한 데이터 요구 사항을 완화한다.

불행하게도 “Autoregressive over X” 아키텍처는 긴 동영상을 생성하는 리소스가 충분한 솔루션인 동시에 새로운 어려움이 생긴다.

1. 모델이 긴 동영상에서 이러한 패턴을 학습할 기회가 없기 때문에 생성된 긴 동영상에서 비현실적인 샷 변경과 장기적인 불일치가 발생할 수 있다.
2. Sliding window의 종속성 제한으로 인해 inference 프로세스가 병렬로 수행될 수 없으므로 훨씬 더 많은 시간이 소요돤다.

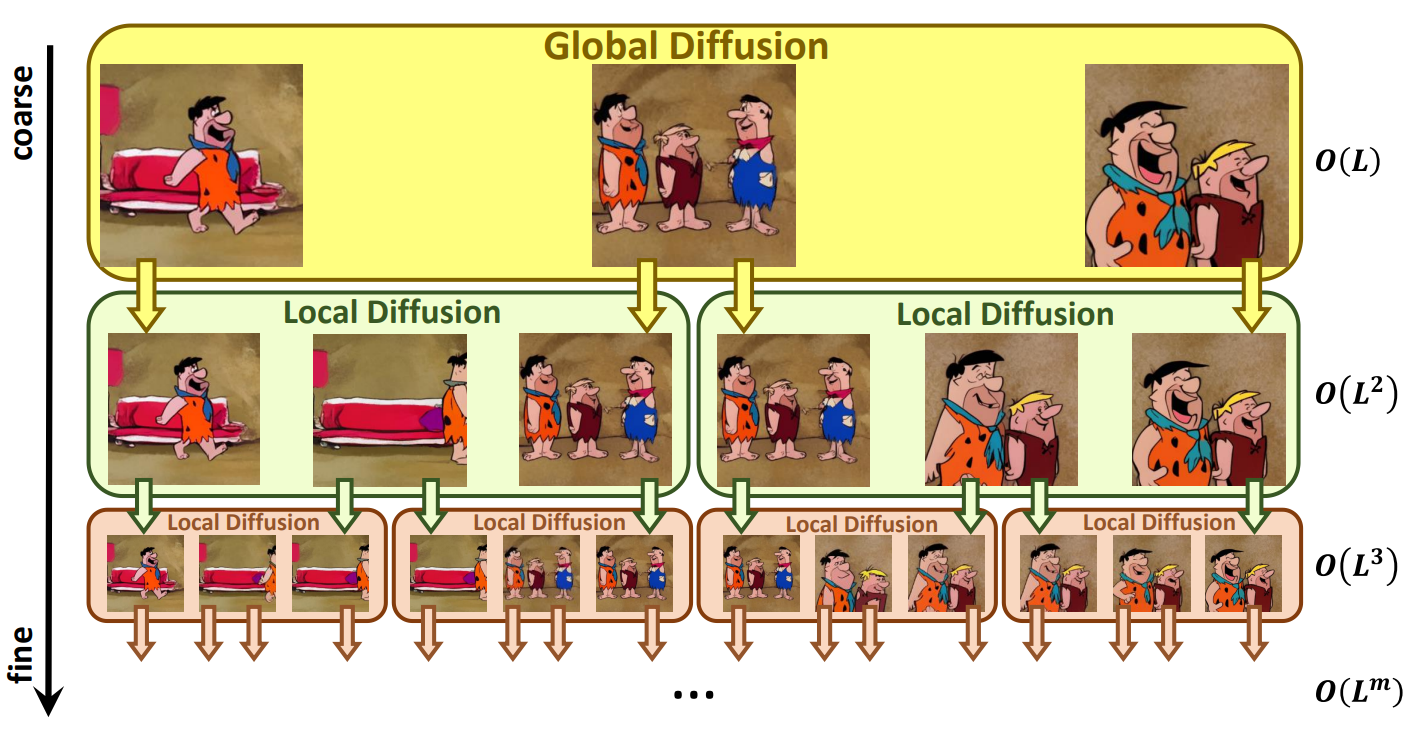
본 논문은 위의 문제를 해결하기 위해 위 그림과 같이 “coarse-to-fine” 프로세스로 긴 동영상을 생성하는 “Diffusion over Diffusion” 아키텍처인 NUWA-XL을 제안한다. 먼저 global diffusion model이 $L$개의 프롬프트를 기반으로 하는 $L$개의 키프레임을 생성하며, 이 키프레임들은 동영상의 대략적인 스토리라인을 형성한다. 첫 번째 local diffusion model은 $L$개의 프롬프트와 인접 키프레임들을 각각 첫 번째와 마지막 프레임으로 취급하여 $L-2$개의 중간 프레임을 생성하여, 총 $L + (L-1)\times(L-2) \approx L^2$개의 디테일한 프레임을 생성한다.

반복적으로 local diffusion을 적용하여 중간 프레임을 채우면 동영상 길이가 기하급수적으로 늘어나 매우 긴 동영상이 된다. 예를 들어 깊이가 $m$이고 local diffusion의 길이가 $L$인 NUWA-XL은 크기가 $O(L^m)$인 긴 동영상을 생성할 수 있다. 이러한 방식의 장점은 세 가지다.

1. 이러한 계층적 아키텍처를 통해 모델이 긴 동영상에서 직접 학습할 수 있으므로 학습과 inference 사이의 불일치가 제거된다.
2. 자연스럽게 병렬 inference를 지원하므로 긴 동영상을 생성할 때 inference 속도를 크게 향상시킬 수 있다.
3. 동영상의 길이가 기하급수적으로 늘어날 수 있기 때문에 더 긴 동영상으로 쉽게 확장될 수 있다.

Method

1. Temporal KLVAE (T-KLVAE)

픽셀에서 diffusion model을 직접 학습하고 샘플링하는 것은 계산 비용이 많이 든다. KLVAE는 diffusion process를 수행하여 이 문제를 완화할 수 있는 저차원 latent 표현으로 원본 이미지를 압축한다. 사전 학습된 이미지 KLVAE의 외부 지식을 활용하고 이를 동영상으로 전송하기 위해, 저자들은 원본 공간적 모듈을 그대로 유지하면서 외부 temporal convolution 및 attention layer를 추가하여 Temporal KLVAE(T-KLVAE)를 제안한다.

Batch size가 $b$, 프레임이 $L$개, 채널이 $C$개, 높이가 $H$, 너비가 $W$인 동영상 $v \in \mathbb{R}^{b \times L \times C \times H \times W}$가 주어지면 먼저 $L$개의 독립 이미지로 보고 사전 학습된 KLVAE spatial convolution으로 인코딩한다. 시간 정보를 추가로 모델링하기 위해 각 spatial convolution 후에 temporal convolution을 추가한다. 원래 사전 학습된 지식을 그대로 유지하기 위해 temporal convolution은 원래 KLVAE와 정확히 동일한 출력을 보장하는 항등 함수로 초기화된다.

구체적으로, convolution 가중치 $W^{conv1d} \in \mathbb{R}^{c_{out} \times c_{in} \times k}$는 먼저 0으로 설정된다. 여기서 $c_{out}$은 출력 채널을 나타내고, $c_{in}$은 입력 채널을 나타내며 $c_{out}$과 같고, $k$는 temporal kernel의 크기를 나타낸다. 그런 다음 각 출력 채널 $i$에 대해 해당 입력 채널 $i$의 kernel 크기의 중간 $(k - 1)//2$이 1로 설정된다.

\[\begin{equation} W^{conv1d}[i, i, (k-1)//2] = 1 \end{equation}\]

비슷하게, 원래 spatial attention 후에 temporal attention을 추가하고 출력 projection layer의 가중치 $W^\textrm{att_out}$을 0으로 초기화한다.

\[\begin{equation} W^\textrm{att_out} = 0 \end{equation}\]

T-KLVAE 디코더 $D$의 경우, 같은 초기화 전략을 사용한다. T-KLVAE의 목적 함수는 이미지 KLVAE와 동일하다. 마지막으로, 원본 동영상 $v$의 컴팩트한 표현인 latent code $x_0 \in \mathbb{R}^{b \times L \times c \times h \times w}$를 얻는다.

2. Mask Temporal Diffusion (MTD)

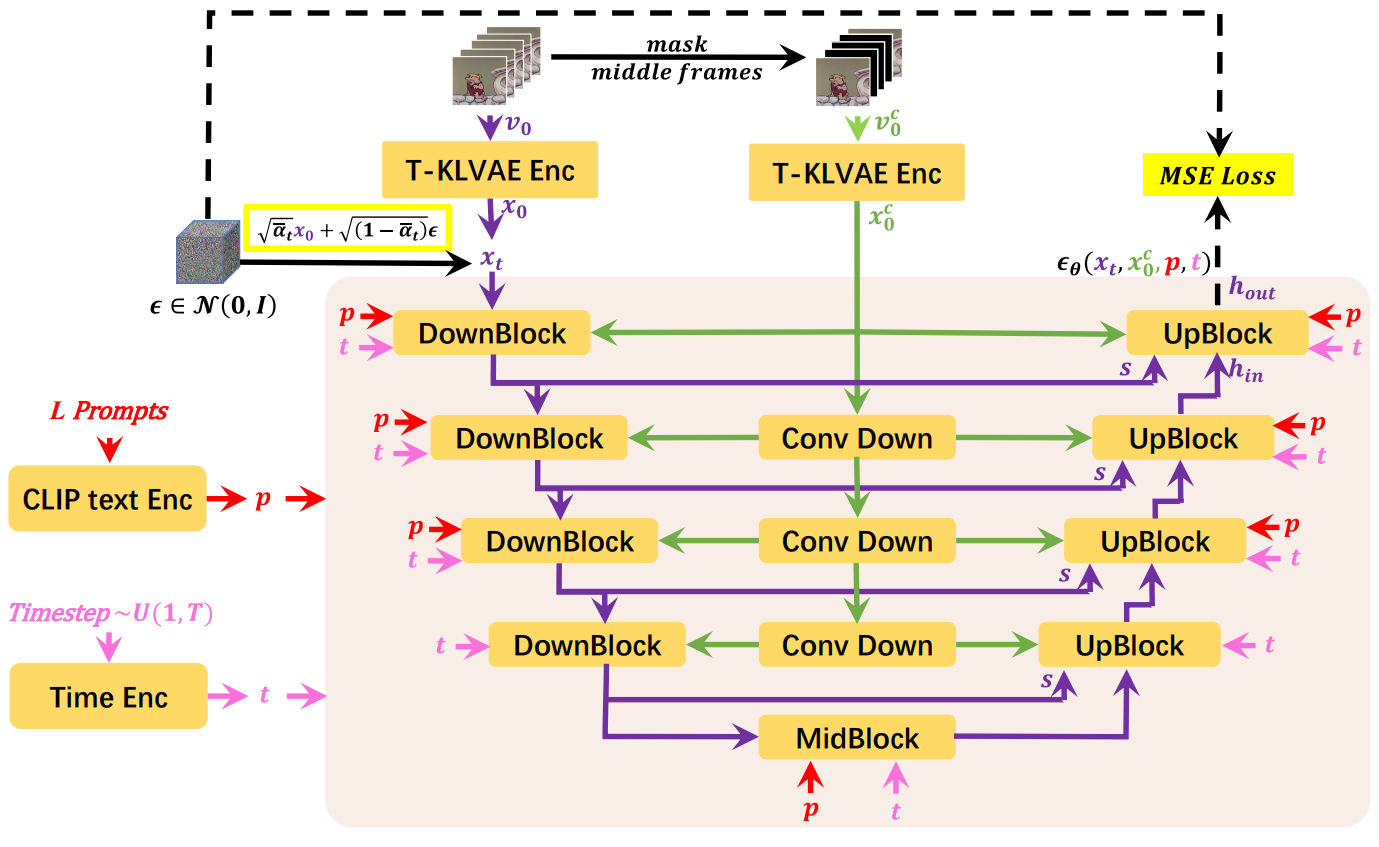
다음으로, 제안된 Diffusion over Diffusion 아키텍처의 기본 diffusion model로 Mask Temporal Diffusion (MTD)를 소개한다. Global diffusion의 경우 $L$개의 프롬프트만 동영상의 대략적인 스토리라인을 형성하는 입력으로 사용되지만 local diffusion의 경우 입력은 $L$개의 프롬프트뿐만 아니라 첫 번째 및 마지막 프레임으로 구성된다. 첫 번째 프레임과 마지막 프레임이 있거나 없는 입력 조건을 수용할 수 있는 제안된 MTD는 global diffusion과 local diffusion을 모두 지원한다.

먼저 $L$개의 프롬프트 입력을 CLIP Text Encoder로 임베딩하여 prompt embedding $p \in \mathbb{R}^{b \times L \times l_p \times d_p}$을 얻는다. 여기서 $b$는 batch size, $l_p$는 토큰의 개수, $d_p$는 prompt embedding의 차원이다. 랜덤하게 샘플링된 diffusion timestep $t \in U(1, T)$는 timestep embedding $t \in \mathbb{R}^c$로 임베딩된다. 동영상 $v_0 \in \mathbb{R}^{b \times L \times C \times H \times W}$은 T-KLVAE로 인코딩되어 $x_0 \in \mathbb{R}^{b \times L \times c \times h \times w}$를 얻는다.

미리 정의된 diffusion process

\[\begin{equation} q(x_t \vert x_{t-1}) = \mathcal{N}(x_t; \sqrt{\alpha_t} x_{t-1}, (1-\alpha_t) I) \end{equation}\]

에 따라 $x_0$는 다음과 같이 손상된다.

\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + (1 - \bar{\alpha}_t) \epsilon, \quad \epsilon \sim \mathcal{N}(0,I) \end{equation}\]

여기서 $\epsilon \in \mathbb{R}^{b \times L \times c \times h \times w}$은 noise이고, $x_t \in \mathbb{R}^{b \times L \times c \times h \times w}$는 diffusion process의 t번째 중간 state이다.

Global diffusion model의 경우, visual condition $v_0^c$는 모두 0이다. 반면, local diffusion model의 경우, $v_0 \in \mathbb{R}^{b \times L \times C \times H \times W}$는 $v_0$의 중간 $L-2$ 프레임을 마스킹하여 얻을 수 있다. $v_0^c$도 T-KLVAE로 인코딩되어 $x_0^c \in \mathbb{R}^{b \times L \times c \times h \times w}$를 얻는다.

마지막으로, $x_t$, $p$, $t$, $x_0^c$가 Mask 3D-UNet $\epsilon_\theta (\cdot)$에 입력된다. 그런 다음 모델은 Mask 3D-UNet의 출력 $\epsilon_\theta (x_t, p, t, x_0^c) \in \mathbb{R}^{b \times L \times c \times h \times w}$과 $\epsilon$ 사이의 거리를 최소화한다.

\[\begin{equation} \mathcal{L}_\theta = \|\epsilon - \epsilon_\theta(x_t, p, t, x_0^c)\|_2^2 \end{equation}\]

Mask 3D-UNet은 skip connection이 있는 multi-scale DownBlocks와 UpBlocks로 구성되는 반면, $x_0^c$는 convolution layer의 cascade를 사용하여 해당 해상도로 downsampling되고 대응되는 DownBlock과 UpBlock에 공급된다.

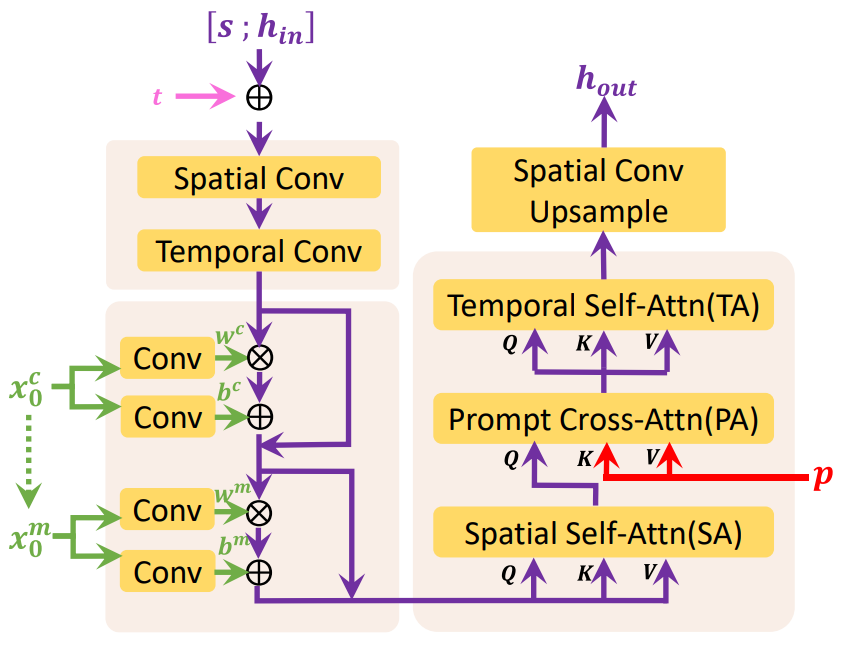
위 그림은 Mask 3D-UNet의 마지막 UpBlock의 디테일을 나타낸 것이다. UpBlock은 hidden state $h_in$, skip connection $s$, timestep embedding $t$, visual condition $x_0^c$, prompt embedding $p$를 입력으로 받아 hidden state $h_out$을 출력한다. Global diffusion의 경우 $x_0^c$은 조건으로 제공되는 프레임이 없기 때문에 유효한 정보를 포함하지 않지만 local diffusion의 경우 $x_0^c$는 첫 번째 프레임과 마지막 프레임의 인코딩된 정보를 포함한다.

$s \in \mathbb{R}^{b \times L \times c_{skip} \times h \times w}$는 먼저 $h_{in} \in \mathbb{R}^{b \times L \times c_{in} \times h \times w}$과 concat된다.

\[\begin{equation} h := [s; h_{in}] \in \mathbb{R}^{b \times L \times (c_{skip} + c_{in}) \times h \times w} \end{equation}\]

$h$는 convolution 연산을 거쳐 $h \in \mathbb{R}^{b \times L \times c \times h \times w}$가 된다. 그런 다음 $t$는 $h$에 채널 차원으로 더해진다.

\[\begin{equation} h := h + t \end{equation}\]

사전 학습된 text-to-image model의 외부 지식을 활용하기 위해, factorized convolution 및 attention이 도입되며, spatial layer 사전 학습된 가중치로 초기화되고 temporal layer는 항등 함수로 초기화된다.

Spatial convolution의 경우, $L$은 batch size로 취급되어 $h \in \mathbb{R}^{(b \times L) \times c \times h \times w}$가 되고, temporal convolution의 경우 공간 축 $hw$가 batch size로 취급되어 $h \in \mathbb{R}^{(b \times hw) \times c \times L}$가 된다.

\[\begin{aligned} h &:= \textrm{SpatialConv}(h) \\ h &:= \textrm{TemporalConv}(h) \end{aligned}\]

그런 다음 $h$는 $x_0^c$와 $x_0^m$으로 컨디셔닝되며, $x_0^m$은 어떤 프레임이 조건인지를 나타내는 이진 마스크이다. $x_0^c$와 $x_0^m$은 먼저 0으로 초기화된 convolution layer에 의해 scale $w^c$, $w^m$과 shift $b^c$, $b^m$으로 변환된다. 그런 다음 linear projection으로 $h$에 주입된다.

\[\begin{aligned} h &:= w^c \cdot h + b^c + h \\ h &:= w^m \cdot h + b^m + h \end{aligned}\]

그런 다음 Spatial Self-Attention (SA), Prompt Cross-Attention (PA), Temporal Self-Attention (TA)을 $h$에 순서대로 적용한다.

SA의 경우, $h$는 $h \in \mathbb{R}^{(b \times L) \times hw \times c}$로 reshape된다.

\[\begin{equation} Q^{SA} = hW_Q^{SA}, \quad K^{SA} = hW_K^{SA}, \quad V^{SA} = hW_V^{SA} \\ \tilde{Q}^{SA} = \textrm{Selfattn} (Q^{SA}, K^{SA}, V^{SA}) \end{equation}\]

$W_Q^{SA}, W_K^{SA}, W_V^{SA} \in \mathbb{R}^{c \times d_{in}}$은 학습되는 파라미터이다.

PA의 경우, $p$는 $p \in \mathbb{R}^{(b \times L) \times l_p \times d_p}$로 reshape된다.

\[\begin{equation} Q^{PA} = hW_Q^{PA}, \quad K^{PA} = pW_K^{PA}, \quad V^{PA} = pW_V^{PA} \\ \tilde{Q}^{SA} = \textrm{Crossattn} (Q^{PA}, K^{PA}, V^{PA}) \end{equation}\]

$W_Q^{PA} \in \mathbb{R}^{c \times d_{in}}$, $W_K^{PA}, W_V^{PA} \in \mathbb{R}^{d_p \times d_{in}}$은 학습되는 파라미터이다.

TA는 SA와 동일하며, 공간 축 $hw$가 batch size로 취급되고 $L$이 시퀀스 길이로 취급되는 것만 다르다.

마지막으로, $h$는 spatial convolution을 통해 목표 해상도 $h_{out} \in \mathbb{R}^{b \times L \times c \times h_{out} \times h_{out}}$로 upsampling된다. 마찬가지로 Mask 3D-UNet의 다른 블록은 동일한 구조를 활용하여 해당 입력을 처리한다.

3. Diffusion over Diffusion Architecture

Inference 단계에서 $L$개의 프롬프트 $p$와 visual condition $v_0^c$가 주어지면 $x_0$는 MTD에 의해 순수 noise $x_T$에서 샘플링된다. 구체적으로, 각 timestep $t = T, T − 1, \cdots, 1$에 대해 diffusion process에서 중간 state $x_t$는 다음과 같이 업데이트된다.

\[\begin{equation} x_{t-1} = \frac{1}{\sqrt{\alpha}_t} \bigg( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (x_t, p, t, x_0^c) \bigg) + \frac{(1 - \bar{\alpha}_{t-1}) \beta_t}{1 - \bar{\alpha}_t} \epsilon \end{equation}\]

마지막으로 샘플링된 latent code $x_0$는 T-KLVAE에 의해 동영상 픽셀 $v_0$로 디코딩된다. 단순화를 위해 MTD의 반복 생성 프로세스는 다음과 같이 표시된다.

\[\begin{equation} v_0 = \textrm{Diffusion} (p, v_0^c) \end{equation}\]

긴 동영상을 생성할 때 큰 간격으로 $L$개의 프롬프트 $p_1$이 주어지면 $L$개의 키프레임은 먼저 global diffusion model을 통해 생성된다.

\[\begin{equation} v_{01} = \textrm{GlobalDiffusion} (p_1, v_{01}^c) \end{equation}\]

여기서 $v_{01}^c$는 모두 0이다. 일시적으로 희소한 키프레임 $v_{01}$은 동영상의 대략적인 스토리라인을 형성한다.

그런 다음 $v_{01}$의 인접한 키프레임은 visual condition $v_{02}^c$의 첫 번째 및 마지막 프레임으로 처리된다. 중간 $L-2$개의 프레임은 $p_2$, $v_{02}^c$를 첫 번째 local diffusion model에 공급하여 생성된다. 여기서 $p_2$는 시간 간격이 더 짧은 $L$개의 프롬프트이다.

\[\begin{equation} v_{02} = \textrm{LocalDiffusion} (p_2, v_{02}^c) \end{equation}\]

비슷하게, $v_{03}^c$는 $v_{02}$의 인접한 프레임에서 얻을 수 있으며, $p_3$는 $p_2$보다 시간 간격이 더 짧은 $L$개의 프롬프트이다. $p_3$와 $v_{03}^c$는 두 번째 local diffusion model에 공급된다.

\[\begin{equation} v_{03} = \textrm{LocalDiffusion} (p_3, v_{03}^c) \end{equation}\]

$v_{01}$의 프레임들과 비교했을 때, $v_{02}$와 $v_{03}$의 프레임들은 더 많은 디테일과 강한 일관성을 가지며 더 세밀해진다.

Local diffusion을 반복적으로 적용하여 중간 프레임을 완성함으로써 깊이가 $m$인 모델은 길이가 $O(L^m)$인 매우 긴 동영상을 생성할 수 있다. 한편, 이러한 계층적 아키텍처를 통해 긴 동영상(3376 프레임)에서 시간적으로 희소하게 샘플링된 프레임을 직접 학습시켜 학습과 inference 사이의 격차를 없앨 수 있다. Global diffusion으로 $L$개의 키프레임을 샘플링한 후 local diffusion을 병렬로 수행하여 추론 속도를 높일 수 있다.

Experiments

1. FlintstonesHD Dataset

기존의 주석이 달린 동영상 데이터셋은 동영상 생성의 발전을 크게 촉진했다. 그러나 현재 동영상 데이터셋은 여전히 긴 동영상 생성에 큰 어려움을 안고 있다.

1. 동영상의 길이가 상대적으로 짧고, 샷 체인지, 장기 의존성 등 짧은 영상과 긴 영상의 분포 격차가 크다.
2. 상대적으로 낮은 해상도는 생성된 비디오의 품질을 제한한다.
3. 대부분의 주석은 비디오 클립의 내용에 대한 대략적인 설명이며 움직임의 디테일을 설명하기 어렵다.

저자들은 위의 문제를 해결하기 위해 조밀하게 주석이 달린 긴 동영상 데이터셋인 FlintstonesHD 데이터셋을 구축하였다. 먼저 1440$\times$1080 해상도의 평균 38,000 프레임으로 166개의 에피소드가 포함된 원본 Flintstones 만화를 얻는다. 스토리를 기반으로 긴 동영상 생성을 지원하고 움직임의 디테일을 캡처하기 위해 먼저 이미지 캡션 모델 GIT2를 활용하여 데이터셋 각 프레임에 대한 조밀한 캡션을 생성하고 생성된 결과에서 일부 오차를 수동으로 필터링한다.

2. Metrics

• Avg-FID: 생성된 프레임들의 평균 FID를 측정한다.
• Block-FVD: 긴 동영상을 여러 개의 짧은 클립으로 나누고 모든 클립들의 평균 FVD를 측정한다. 간단하게 “B-FVD-X”로 나타내며 X는 짧은 클립의 길이를 나타낸다.

3. Quantitative Results

Comparison with the state-of-the-arts

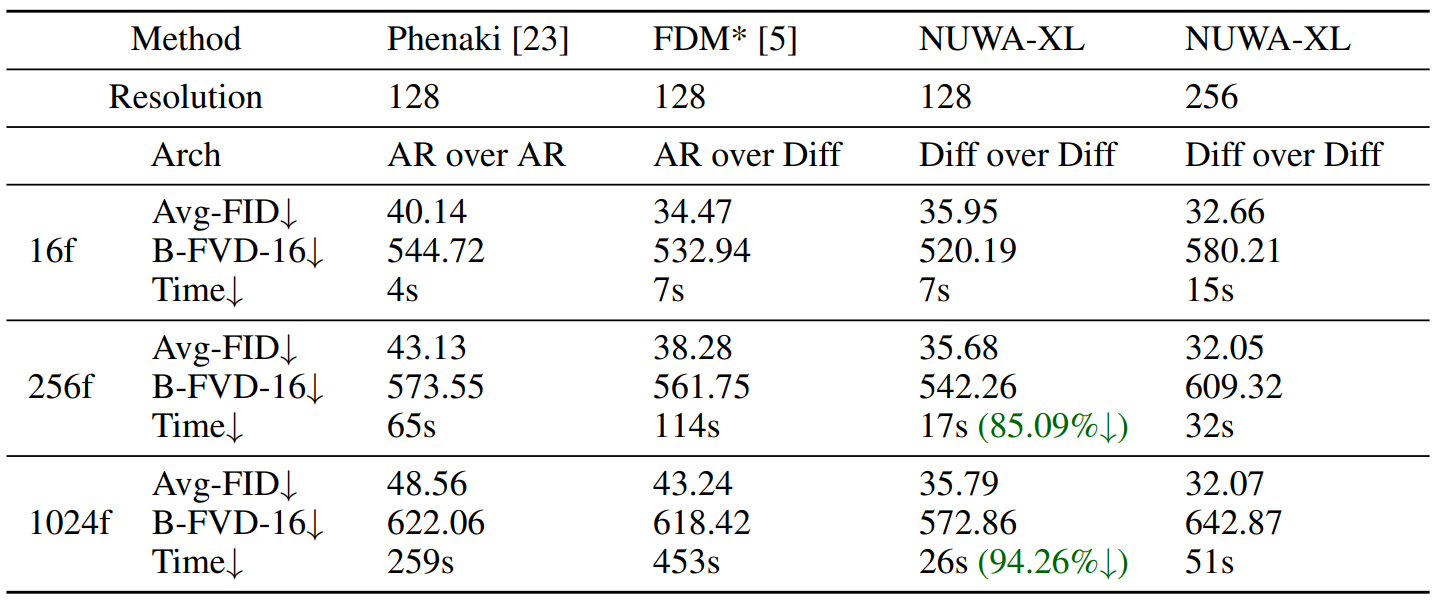
다음은 여러 state-of-the-art model들의 정량적 비교 결과이다.

Ablation study

다음은 ablation 실험 결과이다.

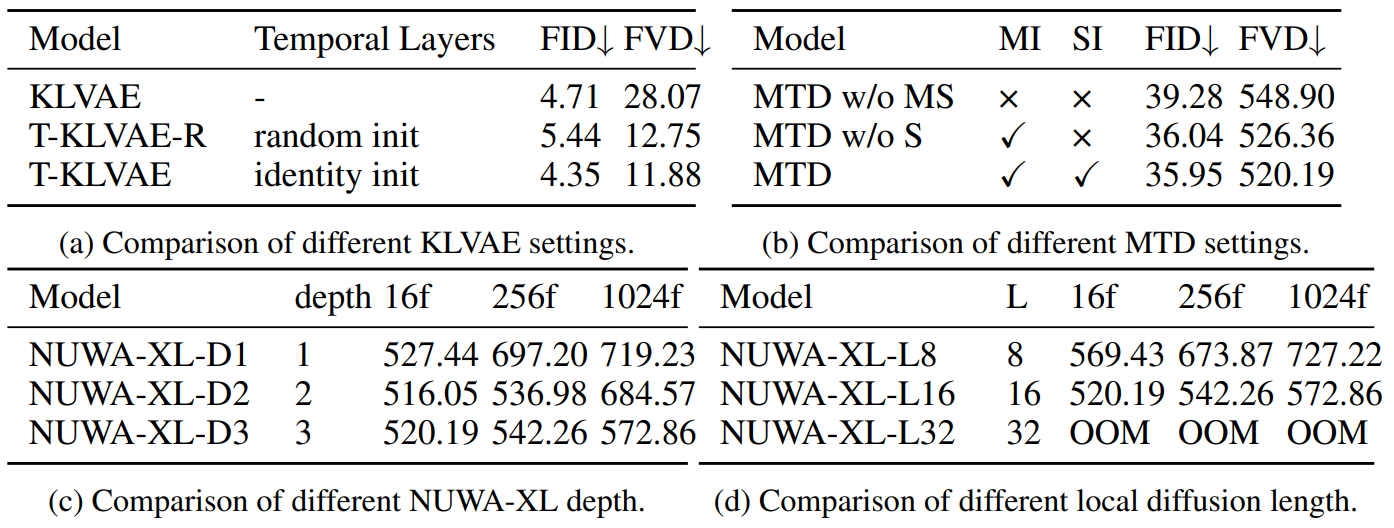
4. Qualitative results

다음은 AR over Diffusion과 Diffusion over Diffusion을 정성적으로 비교한 것이다.

Limitations

1. 오픈 도메인의 긴 동영상(ex. 영화 및 TV 프로그램)을 사용할 수 없기 때문에 공개적으로 사용 가능한 만화 Flintstones에 대해서만 NUWA-XL의 효과를 검증하였다.
2. 긴 동영상에 대한 직접적인 학습은 학습과 inference 사이의 격차를 줄이지만 데이터에 큰 문제를 제기한다.
3. NUWA-XL은 inference 속도를 가속화하려면 병렬 inference를 위한 합리적인 GPU 리소스가 필요하다.