[논문리뷰] NormalCrafter: Learning Temporally Consistent Normals from Video Diffusion Priors
ICCV 2025. [Paper] [Page] [Github]
Yanrui Bin, Wenbo Hu, Haoyuan Wang, Xinya Chen, Bing Wang
The Hong Kong Polytechnic University | Tencent PCG | City University of Hong Kong | Huazhong University of Science and Technology
1 Dec 2024

Introduction
본 논문에서는 임의 길이의 제약 없는 오픈월드 동영상에서 풍부하고 세밀한 디테일을 보여주며 시간적으로 일관된 normal 시퀀스를 생성하는 새로운 동영상 normal 추정 모델인 NormalCrafter를 제안하였다. 이미지 기반 normal 추정 모델에 temporal layer를 점진적으로 통합하거나 복잡한 안정화 테크닉을 고안하는 대신, video diffusion model의 잠재력을 활용하여 보다 robust한 동영상 normal 추정 방식을 제시하였다.
Video diffusion model은 깊이 추정에서 놀라운 성공을 거두었지만, normal 추정은 특히 표면 normal에 내재된 디테일을 보존하는 데 있어 고유한 어려움을 가지고 있다. Video diffusion model을 normal 추정에 그대로 적용하면 normal 예측이 over-smoothing되는 등 최적의 성능을 얻기 어려운 경우가 많다. 이러한 문제를 해결하기 위해, 본 논문에서는 DINO에서 추출한 semantic 표현과 diffusion feature를 정렬하여 모델의 초점을 semantic 측면으로 유도하는 Semantic Feature Regularization (SFR) 기법을 제안하였다.
또한, 최근 연구 결과에 따르면 이미지 기반 깊이 또는 normal 추정에서 latent space 뿐만 아니라 VAE의 최종 출력에 직접 loss를 적용하는 것이 공간적 정확도를 크게 향상시키는 것으로 나타났다. 그러나 이는 압축된 latent space를 고차원 픽셀 공간으로 확장해야 하므로 학습 중 GPU 메모리 사용량을 상당히 증가시킨다. 저자들은 이 문제를 해결하기 위해 2단계 학습 전략을 제안하였다. 첫 번째 단계에서는 전체 모델을 latent space에서 학습시켜 장기적인 시간적 컨텍스트를 효과적으로 포착하고, 두 번째 단계에서는 픽셀 공간에서 spatial layer를 fine-tuning하여 긴 시퀀스 inference 능력을 유지하면서 공간 정확도를 향상시켰다.
Method
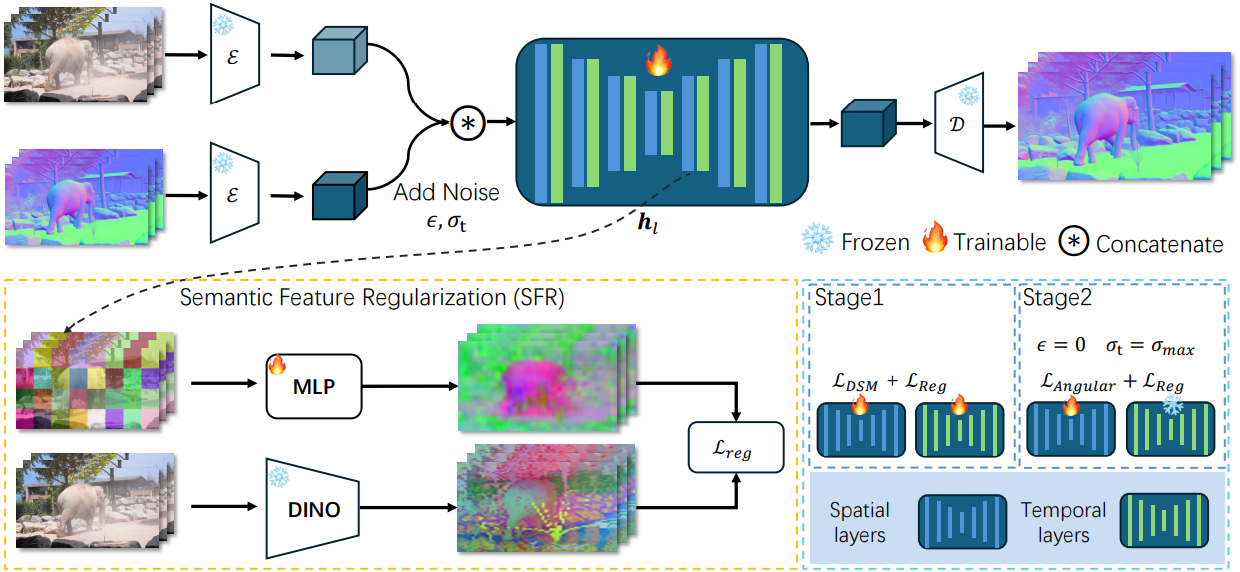
본 논문에서는 video diffusion model (VDM)에서 파생된 동영상 normal 추정 모델인 NormalCrafter를 소개한다. 프레임 수가 $F$인 동영상 \(c \in \mathbb{R}^{F \times W \times H \times 3}\)이 주어졌을 때, 본 논문의 목표는 공간적으로 정확하고 시간적으로 일관된 normal 추정값 \(n \in \mathbb{R}^{F \times W \times H \times 3}\)을 생성하는 것이다.
1. Normal Estimator with VDMs
최신 VDM은 계산 오버헤드를 줄이기 위해 일반적으로 VAE를 활용하여 압축된 latent space에서 작동한다. Normal map은 RGB 이미지 프레임과 동일한 차원을 공유하므로, normal map $n$과 해당 동영상 $c$ 모두에 동일한 VAE를 원활하게 사용할 수 있다.
\[\begin{equation} z^x = \mathcal{E}(x), \quad \hat{x} = \mathcal{D}(z^x) \end{equation}\]($\mathcal{E}$와 $\mathcal{D}$는 각각 VAE의 인코더와 디코더, $x$는 $n$ 또는 $c$, $\hat{x}$는 $x$의 재구성된 결과)
그러나 기존의 대부분의 VAE는 RGB 프레임으로 사전 학습되어 있어 normal map에는 최적화되어 있지 않다. 따라서 본 논문에서는 재구성 품질을 향상시키기 위해 normal 데이터에 맞춰 VAE 디코더를 fine-tuning하였다.
Diffusion 기반 normal 추정
Diffusion 프레임워크에서 normal 추정은 단순 noise 분포에서 입력 동영상 latent $z^c$에 컨디셔닝된 데이터 분포 $p(z^n \vert z^c)$로의 변환이다. 한편, $p(z^n \vert z^c)$를 noise 분포로 매핑하기 위해 각 timestep $t$에서 분산 $\sigma_t^2$를 갖는 Gaussian noise를 latent normal 시퀀스 $z_0^n$에 주입하는 forward diffusion 시퀀스가 적용된다.
\[\begin{equation} z_t^n = z_0^n + \sigma_t^2 \epsilon, \quad \epsilon \sim \mathcal{N}(0,I) \end{equation}\](\(z_t^n \sim p(z^n; \sigma_t)\)는 noise가 섞인 latent normal 시퀀스)
\(\sigma_t\)가 충분히 커지면 \(p(z^n; \sigma_t)\)는 순수한 Gaussian prior와 통계적으로 구별할 수 없게 된다. 반면에 noise 분포를 \(p(z^n \vert z^c)\)로 변환하기 위해 denoising process는 noise 샘플 \(\epsilon \sim \mathcal{N}(0, \sigma_\textrm{max} ^2 I)\)를 추출하고 학습된 denoiser \(D_\theta\)를 통해 반복적으로 $z_0^n$으로 변환한다. 이 denoiser는 denoising score matching (DSM)을 통해 학습된다.
\[\begin{equation} \mathcal{L}_\textrm{DSM} = \mathbb{E}_{z^n \sim p(z^n; \sigma_t), \sigma_t \sim p(\sigma)} \lambda (\sigma_t) \| D_\theta (z_t^n; \sigma_t; z^c) - z_0^n \|_2^2 \\ \textrm{where} \quad \lambda (\sigma_t) = (1 + \sigma_t^2) \sigma_t^{-2} \end{equation}\]본 논문에서는 입력 이미지로부터 동영상을 생성하기 위해 설계된 SVD 모델을 기반으로 NormalCrafter를 구축했다. SVD 프레임워크를 사용하기 위해, 저자들은 이미지 입력을 noise가 포함된 latent normal $z_t^n$와 동영상 latent $z^c$의 프레임별 concat으로 대체하였다.
2. Semantic Feature Regularization

SVD는 원래 단일 입력 이미지에 대한 컨디셔닝을 위해 설계되었기 때문에 여러 프레임으로 구성된 시퀀스로 확장될 경우 컨텍스트 정보를 효과적으로 축적하는 데 어려움을 겪을 수 있다. 위 그림에서 볼 수 있듯이, 초기 SVD 중간 feature는 semantic 모호성을 나타낸다. 예를 들어, 배경의 돌 영역이 과도하게 흐려져 원본 프레임에서 명확하게 드러나는 상세한 기하학적 구조와 모순된다. 결과적으로, SVD를 직접 활용하면 over-smoothing된 normal map이 생성된다. 반면, DINO feature는 입력 프레임의 기하학적 구조와 강한 상관관계를 보이며, 돌과 식물 영역 모두에 대한 정교한 표현을 통해 이를 확인할 수 있다.
저자들은 semantic feature를 diffusion model에 통합하여 normal 추정의 정확도를 더욱 향상시키고자 하였다. 이를 위해 가장 간단한 접근 방식은 DINO feature를 추가적인 컨디셔닝 요소로 diffusion model에 추가하는 것이다. 그러나 이러한 방식은 학습 및 inference 과정에서 상당한 계산 및 메모리 오버헤드를 발생시킨다.
따라서 본 논문에서는 REPA에서 영감을 받아, 학습 과정 전반에 걸쳐 robust한 semantic 표현을 사용하여 SVD feature의 semantic 모호성을 해결하는 Semantic Feature Regularization (SFR) 기법을 제안하였다. 이러한 정렬을 통해 diffusion model은 입력 프레임의 semantics에 집중하게 되어 더욱 정확하고 세밀한 normal map을 생성할 수 있다. 또한, SFR은 학습 과정에서만 오버헤드를 발생시키며, inference 과정에는 추가적인 비용 부담을 주지 않는다.
구체적으로, 먼저 입력 동영상 프레임 $c$로부터 DINO feature는 \(h_\textrm{dino} = f(c) \in \mathbb{R}^{N \times D}\)를 추출한다. 그런 다음, diffusion model의 $l$번째 레이어에서 중간 feature는 $h_l$을 추출하고, 학습 가능한 MLP $h_\phi$를 사용하여 이를 DINO feature space로 projection한다. 마지막으로, 패치별 cosine similarity를 최대화하여 projection된 feature들을 DINO feature와 일치하도록 정규화한다.
\[\begin{equation} \mathcal{L}_\textrm{reg} = - \mathbb{E}_c \left[ \frac{1}{N} \sum_{p=1}^P \textrm{cossim}(h_\textrm{dino}^{[p]}, h_\phi (h_l^{[p]})) \right] \end{equation}\]($p$은 패치 인덱스, $\textrm{cossim}$은 cosine similarity function)
3. Two-Stage Training Protocol
Loss \(\mathcal{L}_\textrm{DSM} + \mathcal{L}_\textrm{reg}\)를 사용하여 latent space에서 NormalCrafter를 학습시키는 것은 가능하지만, E2E-FT에서 강조된 바와 같이 정확도나 효율성 측면에서 최적의 결과를 얻지 못할 수 있다. 대신, 본 논문에서는 깊이 및 normal 추정을 위한 단일 end-to-end step에서 이미지 diffusion model을 fine-tuning하여 이미지 공간에서 pixel-wise loss를 직접 최적화함으로써 향상된 효율성과 함께 우수한 공간적 충실도를 달성하는 방법을 제안하였다. 그러나 이러한 접근 방식을 동영상 normal 추정에 확장하면 loss을 계산하기 위해 latent normal 시퀀스를 픽셀 공간으로 디코딩하는 데 VAE를 사용해야 하므로 메모리 요구량이 급격히 증가하며, 학습 클립의 길이가 크게 제한된다.
이를 위해, 본 논문에서는 긴 시간적 컨텍스트 모델링의 필요성과 높은 정밀도의 공간적 충실도를 효과적으로 균형 있게 조절하는 2단계 학습 프로토콜을 제안하였다. 먼저 \(\mathcal{L}_\textrm{DSM} + \mathcal{L}_\textrm{reg}\)를 사용하여 latent space에서 NormalCrafter를 학습시킨다. 이 단계에서 시퀀스 길이는 $[1, 14]$에서 무작위로 샘플링되므로 NormalCrafter는 다양한 동영상 길이에 유연하게 적응할 수 있다. 또한, 이러한 설정은 단일 프레임 및 다중 프레임 동영상 데이터셋 모두에서 학습을 용이하게 한다.
두 번째 단계에서는 latent normal 시퀀스를 픽셀 공간으로 디코딩하고 \(\mathcal{L}_\textrm{angular} + \mathcal{L}_\textrm{reg}\)를 사용하여 spatial layer만 fine-tuning한다. \(\mathcal{L}_\textrm{angular}\)는 다음과 같이 정의된다.
\[\begin{equation} \mathcal{L}_\textrm{angular} = \frac{1}{HW} \sum_{i,j} \textrm{arccos} \left( \frac{n_{i,j}^\ast \cdot \hat{n}_{i,j}}{\| n_{i,j}^\ast \| \| \hat{n}_{i,j} \|} \right) \end{equation}\](\(n_{i,j}^\ast\)과 \(\hat{n}_{i,j}\)는 픽셀 $(i, j)$에서의 GT normal과 예측된 normal)
이 두 번째 단계에서는 $[1, 4]$에서 시퀀스 길이를 무작위로 샘플링하여 GPU 메모리 제약을 완화한다. 모델은 첫 번째 단계에서 장기적인 시간적 단서를 이미 습득했고, 두 번째 단계에서는 spatial layer만 정밀하게 조정하기 때문에, 이 2단계 프로토콜을 통해 모델은 방대한 시퀀스를 처리하는 능력을 유지하면서 end-to-end fine-tuning의 이점을 누릴 수 있다.
Experiments
- 학습 데이터셋: Replica, 3D Ken Burns, Hypersim, MatrixCity, Objaverse
- 구현 디테일
- $h_\phi$는 3-layer MLP
- $h_l$은 U-Net 디코더의 두 번째 up block의 출력 feature
- learning rate & iteration
- VAE: learning rate = $1 \times 10^{-5}$, 2만 iteration
- U-Net 1단계: learning rate = $3 \times 10^{-5}$, 2만 iteration
- U-Net 2단계: learning rate = $1 \times 10^{-5}$, 1만 iteration
- optimizer: AdamW (100-step wrarm-up, exponential decay)
- batch size: 8 (GPU당 1)
- VAE fine-tuning에 1일, U-Net fine-tuning에 1.5일 소요
1. Evaluations
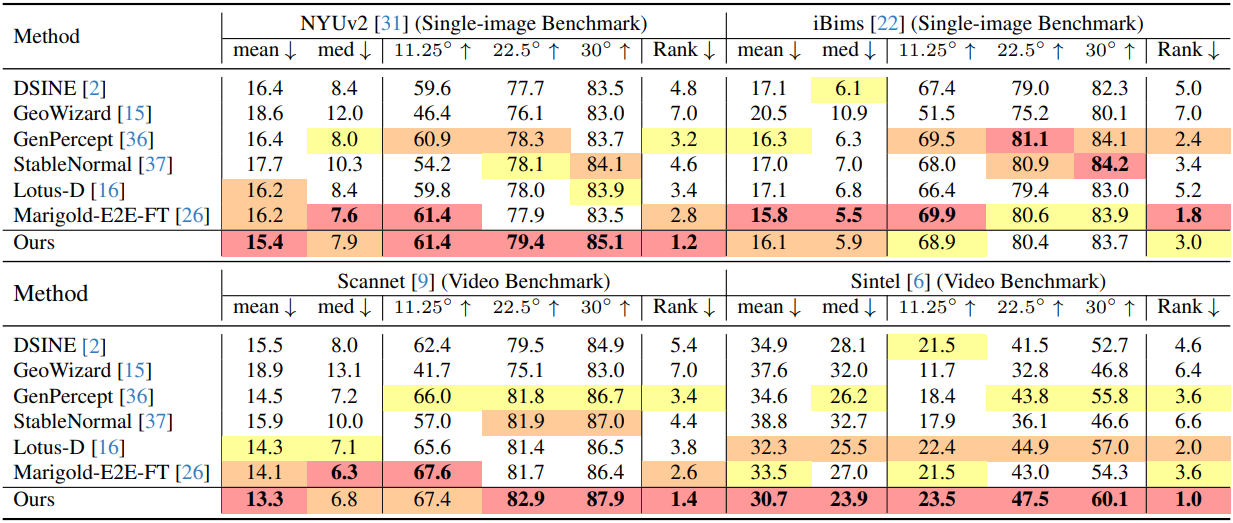
다음은 normal 추정 성능을 정량적으로 비교한 결과이다.
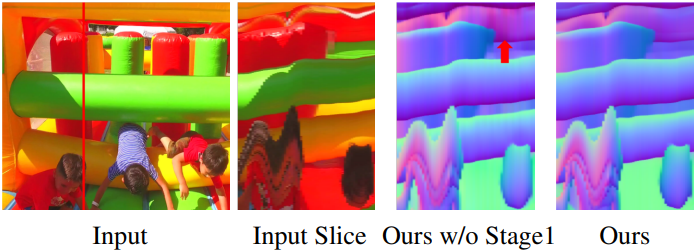
다음은 DAVIS 데이터셋과 Sora로 생성한 동영상들에 대한 비교 결과이다.

2. Ablation study
다음은 ablation study 결과이다.


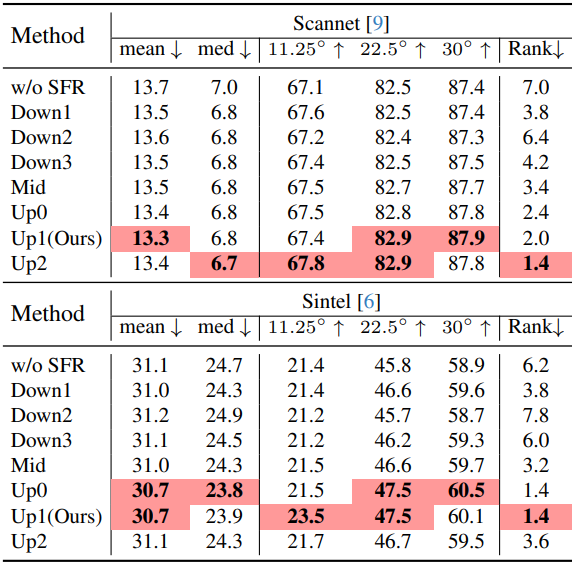
다음은 SFR 위치에 대한 영향을 비교한 결과이다.
Limitations
파라미터 크기가 커서 모바일 기기 배포에 어려움이 있다.