[논문리뷰] On the Importance of Noise Scheduling for Diffusion Models (Tech Report)
arXiv 2023. [Paper]
Ting Chen
Google Research, Brain Team
26 Jan 2023

Why is noise scheduling important for diffusion models?
Diffusion model은 $x_t = \sqrt{\gamma(t)} x_0 + \sqrt{1 - \gamma(t)} \epsilon$로 데이터의 noising process를 정의한다. 여기서 $x_0$는 입력 예시이고 $\epsilon$은 등방성 가우시안 분포의 샘플이다. $t$는 0과 1 사이의 연속적인 수이다. Diffusion model의 학습은 간단하다. 먼저 $t \in \mathcal{U} (0, 1)$을 샘플링하여 입력 예제 $x_0$을 $x_t$로 확산시킨 다음 denoising process $f(x_t)$를 학습시켜 noise $\epsilon$이나 깨꿋한 데이터 $x_0$를 예측한다. $t$는 균일하게 분포되므로 noise schedule $\gamma(t)$는 신경망이 학습되는 noise level의 분포를 결정한다.

Noise schedule의 중요성은 위 그림의 예에서 확인할 수 있다. 이미지 크기를 늘리면 동일한 noise level (즉, 동일한 $\gamma$)에서 denoising 연산이 더 간단해진다. 이는 데이터의 정보 중복성 (ex. 인근 픽셀 간의 상관 관계)이 일반적으로 이미지 크기에 따라 증가하기 때문이다. 또한 noise가 각 픽셀에 독립적으로 추가되므로 이미지 크기가 커질 때 원래 신호를 더 쉽게 복구할 수 있다. 따라서 더 작은 해상도의 최적 schedule은 더 높은 해상도에서는 최적이 아닐 수 있다. 그리고 그에 따라 schedule을 조정하지 않으면 특정 noise level에 대한 학습이 부족해질 수 있다.
Strategies to adjust noise scheduling
본 논문은 noise scheduling과 관련된 기존 연구들을 기반으로 diffusion model에 대한 두 가지 서로 다른 noise scheduling 전략을 체계적으로 연구하였다.
1. Strategy 1: changing noise schedule functions

첫 번째 전략은 1차원 함수를 사용하여 parameterize된 noise schedule을 만드는 것이다. 여기에서는 temperature scheduling과 함께 코사인 또는 시그모이드 함수의 일부를 기반으로 한 함수를 사용한다. 이 두 가지 유형의 함수 외에 저자들은 $\gamma (t) = 1 − t$인 간단한 선형 noise schedule 함수를 추가로 제안한다. Algorithm 1은 연속 시간 noise schedule 함수 $\gamma(t)$의 인스턴스화에 대한 코드를 제공한다.
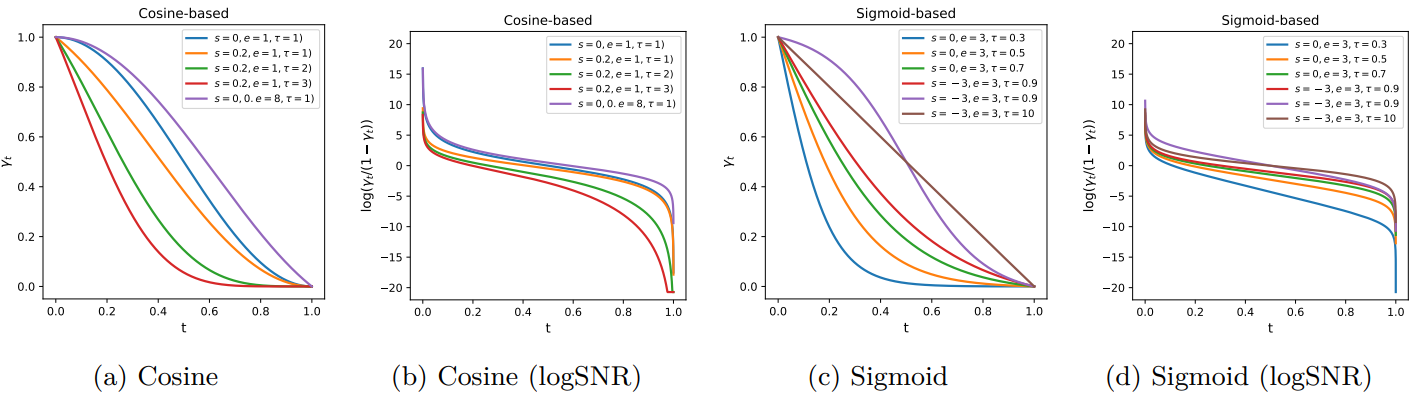
위 그림은 다양한 hyperparameter 선택에 따른 noise schedule 함수와 해당 logSNR (신호 대 잡음비)을 시각화한 것이다. 코사인 함수와 시그모이드 함수 모두 풍부한 noise 분포의 집합을 parameterize할 수 있음을 알 수 있다. 여기에서는 noise 분포가 더 noise가 많은 level로 치우쳐지도록 hyperparameter를 선택하며, 이는 더 유용하다고 생각된다.
2. Strategy 2: adjusting input scaling factor
Noise scheduling을 간접적으로 조정하는 또 다른 방법은 입력 $x_0$를 상수 $b$로 스케일링하는 것이다. 그러면 다음과 같은 noise 처리가 발생한다.
\[\begin{equation} x_t = \sqrt{\gamma (t)} b x_0 + \sqrt{1 - \gamma(t)} \epsilon \end{equation}\]Scaling factor $b$를 줄이면 아래 그림에서 볼 수 있듯이 noise level이 증가한다.

$b \ne 1$일 때 $x_0$의 평균과 분산이 같더라도 $x_t$의 분산은 변경될 수 있으며 이로 인해 성능이 저하될 수 있다. 이 경우, 분산이 고정된 상태로 유지되도록 하기 위해 $x_t$를 $\frac{1}{(b^2 − 1)\gamma(t)+1}$의 factor로 스케일링할 수 있다. 그러나 저자들은 실제로는 $x_t$를 분산으로 정규화하여 $x_t$를 denoising network $f(\cdot)$에 공급하기 전에 단위 분산을 가지도록 보장하면 잘 작동한다는 것을 알 수 있다. 이 분산 정규화 연산은 denoising network의 첫 번째 레이어로도 볼 수 있다.
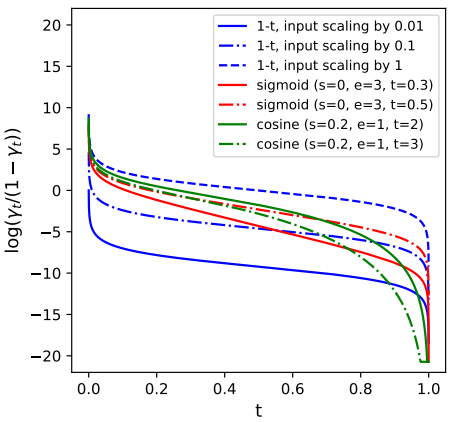
이 입력 스케일링 전략은 위의 noise scheduling 함수 $\gamma(t)$를 변경하는 것과 유사하지만, 위 그림에 표시된 것처럼 특히 $t$가 0에 가까울 때 코사인 및 시그모이드 schedule과 비교할 때 logSNR에서 약간 다른 효과를 얻는다. 실제로 입력 scheduling은 모양을 변경하지 않고 유지하면서 y축을 따라 logSNR을 이동하는데, 이는 위에서 고려한 모든 noise schedule 함수와 다르다. 입력 크기 조정을 피하기 위해 다른 방법으로 $\gamma(t)$ 함수를 동등하게 parameterize할 수도 있다.
3. Putting it together: a simple compound noise scheduling strategy
저자들은 $\gamma(t) = 1−t$와 같은 단일 noise schedule 함수를 사용하고 $b$의 factor로 입력을 스케일링하여 이 두 가지 전략을 결합하는 것을 제안하였다. 학습 및 inference 전략은 다음과 같다.
학습 전략
Algorithm 2는 결합된 noise scheduling 전략을 diffusion model 학습에 통합하는 방법을 보여주며 주요 변경 사항은 파란색으로 강조 표시되어 있다.

Inference/샘플링 전략
학습 중에 분산 정규화가 사용되는 경우 샘플링 중에도 사용해야 한다. 즉, 정규화는 denoising network의 첫 번째 레이어로 볼 수 있다. 연속적인 timestep $t \in [0, 1]$를 사용하므로 inference schedule이 학습 schedule과 동일할 필요는 없다. Inference 중에 0과 1 사이의 시간을 주어진 step 수로 균일하게 discretize한 다음 원하는 $\gamma(t)$ 함수를 선택하여 inference 시간의 noise level을 결정할 수 있다. 실제로 저자들은 표준 코사인 schedule이 샘플링에 적합하다는 것을 확인했다.

Experiments
- 데이터셋: ImageNet
- 구현 디테일
- RIN의 모델 사양을 따르지만 더 작은 모델과 더 짧은 학습 step을 사용
- optimizer: LAMB ($\beta_1$ = 0.9, $\beta_2$ = 0.999)
- weight decay: 0.01
- self-conditioning 비율: 0.9
- EMA decay: 0.9999
모델 hyperparameter는 아래 표와 같다.

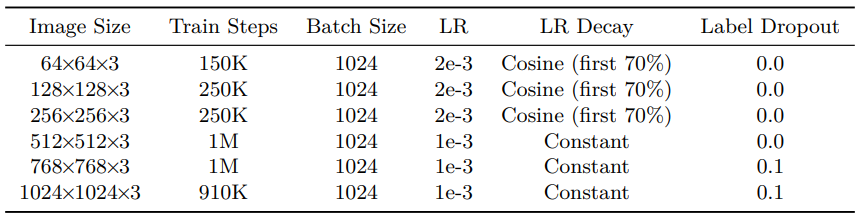
학습 hyperparameter는 아래 표와 같다.
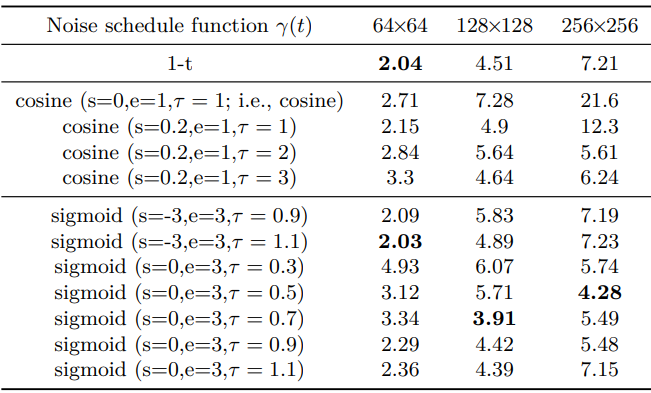
1. The effect of strategy 1 (noise schedule functions)
다음은 다양한 noise schedule 함수에 대하여 FID를 비교한 표이다. 입력 스케일링은 1로 고정된다.
2. The effect of strategy 2 (input scaling)
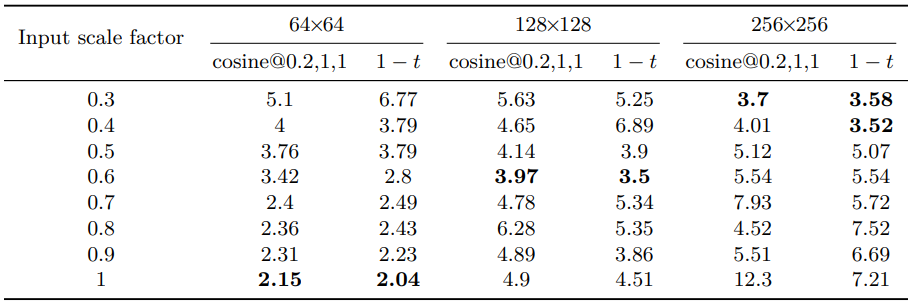
다음은 다양한 입력 scaling factor에 대하여 FID를 비교한 표이다.
3. Quantitative comparison
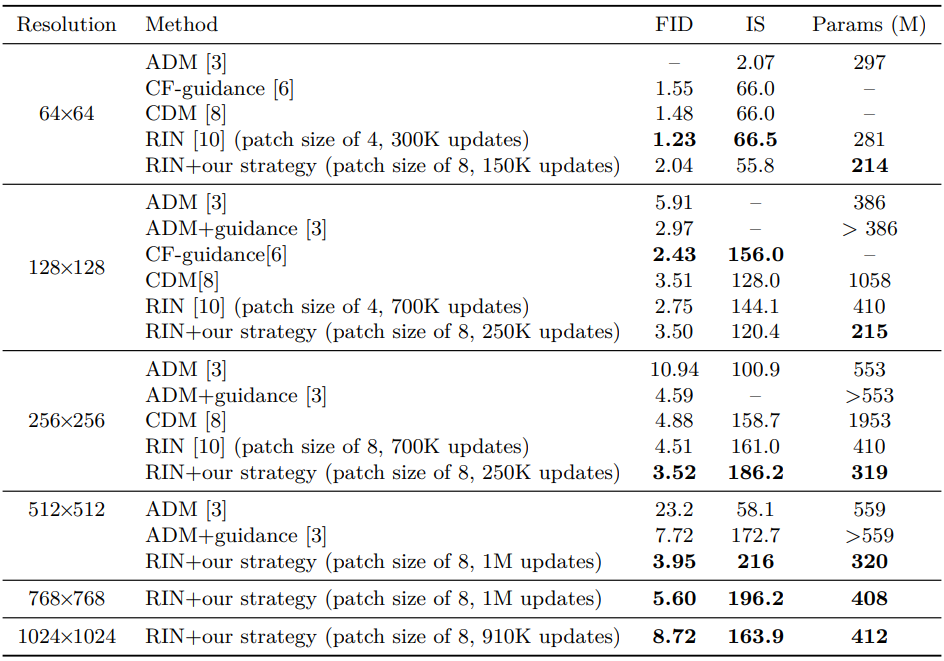
다음은 SOTA 클래스 조건부 픽셀 기반 이미지 생성 모델과 성능을 비교한 표이다. RIN과 결합된 간단한 복합 전략으로 픽셀 기반의 SOTA 1단계 고해상도 이미지 생성이 가능하다.
4. Visualization of generated samples
다음은 512$\times$512 해상도에서 본 논문의 모델이 생성한 랜덤 샘플들이다.

다음은 768$\times$768 해상도에서 본 논문의 모델이 생성한 랜덤 샘플들이다.

다음은 1024$\times$1024 해상도에서 본 논문의 모델이 생성한 랜덤 샘플들이다.
