[논문리뷰] NeuralField-LDM: Scene Generation with Hierarchical Latent Diffusion Models
CVPR 2023. [Paper] [Page]
Seung Wook Kim, Bradley Brown, Kangxue Yin, Karsten Kreis, Katja Schwarz, Daiqing Li, Robin Rombach, Antonio Torralba, Sanja Fidler
NVIDIA | University of Toronto | Vector Institute | CSAIL, MIT | University of Waterloo | Tubingen AI Center | LMU Munich
19 Apr 2023

Introduction
현실 세계 3D scene 모델링에 대한 관심이 높아지고 있다. 그러나 수작업으로 3D 세계를 설계하는 것은 3D 모델링 전문 지식과 예술적 재능이 필요한 까다롭고 시간이 많이 걸리는 프로세스다. 최근에는 개별 개체 에셋을 출력하는 3D 생성 모델을 통해 3D 콘텐츠 생성을 자동화하는 데 성공했다. 큰 진전이지만 실제 scene의 생성을 자동화하는 것은 여전히 중요한 open problem으로 남아 있다.
본 논문에서는 복잡한 실제 3D scene을 합성할 수 있는 생성 모델인 NeuralField-LDM (NF-LDM)을 사용하여 이 목표를 향해 한 걸음 더 나아간다. NF-LDM은 3D scene을 합성하는 확장 가능한 방법을 제공하는 ground-truth 3D 데이터보다 쉽게 얻을 수 있는 카메라 이미지 및 깊이 측정 컬렉션에 대해 학습한다.
최근 접근 방식들은 덜 복잡한 데이터에도 불구하고 3D scene을 생성하는 동일한 문제를 해결하였다. Latent 분포를 적대적 학습(adversarial learning)을 사용하여 scene 집합에 매핑하거나 diffusion model이 auto-decoder를 사용하여 학습된 scene latent 셋에 피팅하였다. 이러한 모델들은 모두 전체 scene을 단일 벡터로 캡처하여 neural radiance field (NeRF)를 컨디셔닝하하려는 고유한 약점이 있다. 실제로 저자들은 이것이 복잡한 scene 분포에 맞추는 능력을 제한한다는 것을 발견했다.
최근, diffusion model은 고품질 이미지, 포인트 클라우드, 동영상을 생성할 수 있는 매우 강력한 생성 모델 클래스로 등장했다. 그러나 명확한 ground-truth 3D 표현 없이 이미지 데이터를 공유된 3D scene에 매핑해야 하므로 모델을 데이터에 직접 맞추는 간단한 접근 방식은 사용할 수 없다.
NF-LDM에서는 3단계 파이프라인을 사용하여 scene을 모델링하는 방법을 학습한다. 먼저 밀도 및 feature voxel grid로 표현되는 neural field로 scene을 인코딩하는 auto-encoder를 학습한다. 이미지에 대한 LDM의 성공에 영감을 받아 latent space에서 scene voxel의 분포를 모델링하여 voxel auto-encoder에서 캡처한 외부 디테일이 아닌 scene의 핵심 부분에 생성을 집중시키는 방법을 학습한다. 특히 latent auto-encoder는 scene voxel을 3D coarse latent, 2D fine latent, 1D global latent로 분해한다. Hierarchichal diffusion model은 새로운 3D scene을 생성하기 위해 이 3개의 latent 표현에 대해 학습된다. 마지막으로 score distillation을 사용하여 생성된 neural field의 품질을 최적화하여 훨씬 더 많은 데이터에 노출된 SOTA 이미지 diffusion model에서 학습한 표현을 활용한다.
NeuralField-LDM
본 논문의 목표는 임의의 viewpoint로 렌더링할 수 있는 3D scene을 합성하기 위해 생성 모델을 학습시키는 것이다. $N$개의 RGB 이미지 $i$와 해당 카메라 포즈 $\kappa$, 깊이 측정값 $\rho$로 구성된 데이터셋 \(\{(i, \kappa, \rho)\}_{1..N}\)에 대한 액세스를 가정한다. 생성 모델은 센서의 관찰로만 학습하여 3D에서 데이터셋의 텍스처 및 형상 분포를 모두 모델링하는 방법을 학습해야 하며, 이는 매우 사소한 문제이다.
이전 연구들은 일반적으로 GAN 프레임워크로 이 문제를 해결했다. 그들은 중간 3D 표현을 생성하고 볼륨 렌더링을 사용하여 주어진 viewpoint에 대한 이미지를 렌더링한다. Discriminator loss는 3D 표현이 모든 viewpoint에서 유효한 이미지를 생성하는지 확인한다. 그러나 GAN에는 악명 높은 학습 불안정성과 mode collapse가 존재한다. Diffusion model은 앞서 언급한 단점을 피하는 GAN의 대안으로 최근 등장했지만 데이터 likelihood를 명시적으로 모델링하고 학습 데이터를 재구성하도록 학습된다. 따라서 실제 3D 데이터를 대규모로 쉽게 사용할 수 없기 때문에 제한된 시나리오에서 사용되었다.
1. Scene Auto-Encoder
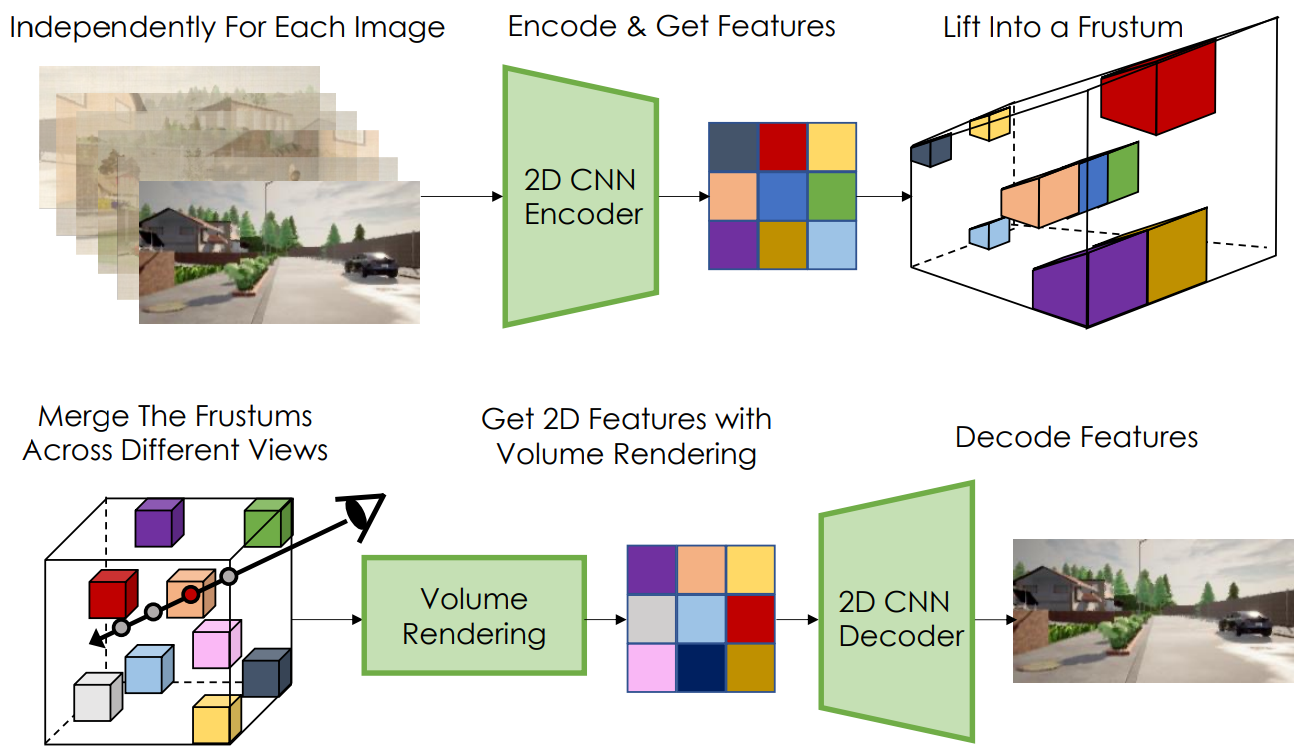
Scene auto-encoder의 목표는 입력 이미지를 재구성하는 방법을 학습하여 입력 이미지에서 scene의 3D 표현을 얻는 것이다. 위 그림은 auto-encoding 프로세스를 보여준다. Scene encoder는 2D CNN이며 각 RGB 이미지 $i_{1..N}$을 개별적으로 처리하여 각 이미지에 대해 $\mathbb{R}^{H \times W \times (D + C)}$ 차원 2D 텐서를 생성한다. 여기서 $H$와 $W$는 $i$의 크기보다 작다. LiftSplat-Shoot (LSS)와 유사한 절차를 따라 각 2D 이미지 feature map을 lift하고 공통 voxel 기반 3D neural field에서 결합한다. 각 이미지에 대해 카메라 포즈 $\kappa$를 사용하여 $H \times W \times D$ 크기의 이산적인 절두체(frustum)를 만든다. 이 절두체에는 미리 정의된 깊이가 $D$인 이산 집합을 따라 각 픽셀에 대한 이미지 feature 및 밀도 값이 포함된다. LSS와 달리 2D CNN 출력의 처음 $D$ 채널을 밀도 값으로 사용한다. 즉, 픽셀 $(h, w)$에 있는 CNN 출력의 $d’$ 채널은 $(h, w, d)$에 있는 절두체 entry의 밀도 값이 된다. 볼륨 렌더링 방정식과 유사하게 밀도 값 $\sigma \ge 0$을 사용하여 절두체에서 각 요소 $(h, w, d)$의 점유 가중치 $O$를 얻는다.
여기서 $h$, $w$는 절두체의 픽셀 좌표를 나타내고 $\delta_j$는 절두체의 각 깊이 사이의 거리다. 점유 가중치를 사용하여 CNN 출력의 마지막 $C$ 채널을 절두체 $F$에 넣는다.
\[\begin{equation} F(h, w, d) = [O(h, w, d) \phi (h, w), \sigma (h, w, d)] \end{equation}\]여기서 $\phi (h, w)$는 깊이 $d$에서 $F$에 대해 $O(h, w, d)$로 스케일링된 픽셀 $(h, w)$의 $C$ 채널 feature 벡터이다.
각 뷰에 대한 절두체를 구성한 후 절두체를 world 좌표로 변환하고 밀도 및 feature voxel grid로 표시되는 공유 3D neural field로 융합한다. $V_\textrm{Density}$와 $V_\textrm{Feat}$를 각각 밀도와 feature grid라고 하자. 밀도 및 feature grid가 있는 scene을 나타내는 이 공식은 최적화 기반 scene 재구성을 위해 이전에 탐색되었으며 scene auto-encoder의 중간 표현으로 활용한다. $V_\textrm{Density, Feat}$는 동일한 공간적 크기를 가지며 $V$의 각 voxel은 world 좌표계의 영역을 나타낸다. $(x, y, z)$로 인덱싱된 각 voxel에 대해 해당 절두체 entry의 모든 밀도와 feature을 pooling한다. 본 논문에서는 단순히 pooling된 feature의 평균을 취한다.
마지막으로 카메라 포즈 $\kappa$를 사용하여 볼륨 렌더링을 수행하여 $V$를 2D feature map에 project한다. 카메라 광선을 따라 각 샘플링 지점에 대한 feature와 밀도를 얻기 위해 각 voxel의 값을 trilinearly interpolate한다. 그런 다음 2D feature은 출력 이미지 $\hat{i}$를 생성하는 CNN 디코더에 입력된다. 이미지를 출력하기 위한 voxel의 렌더링을 $i = r(V, \kappa)$로 나타낸다. 볼륨 렌더링 프로세스에서 각 광선을 따라 예상되는 깊이 $\hat{\rho}$도 얻는다. Scene auto-encoding 파이프라인은 이미지 reconstruction loss $||i − \hat{i} ||$와 depth supervision loss $||\rho − \hat{\rho}||$로 학습된다. Sparse 깊이 측정의 경우 깊이가 기록된 픽셀만 supervise한다.
2. Latent Voxel Auto-Encoder
Voxel grid에 생성 모델을 피팅하는 것이 가능하다. 그러나 실제 scene을 캡처하려면 표현의 차원이 SOTA diffusion model이 학습할 수 있는 것보다 훨씬 커야 한다. 예를 들어 Imagen은 256$\times$256 RGB 이미지에서 학습되고 32개 채널이 있는 128$\times$128$\times$32 크기의 voxel을 사용한다. 따라서 latent auto-encoder (LAE)를 도입하여 voxel을 128차원 global latent, 채널 차원이 4이고 공간 차원이 32$\times$32$\times$16인 coarse (3D) latent, 채널 차원이 4이고 공간 차원이 128$\times$128인 fine (2D) latent로 압축한다.
채널 차원을 따라 $V_\textrm{Density}$와 $V_\textrm{Feat}$를 연결하고 별도의 CNN 인코더를 사용하여 voxel grid $V$를 1D global latent $g$, 3D coarse latent $c$, 2D fine latent $f$의 세 가지 latent의 계층으로 인코딩한다. 저자들은 2D CNN이 3D CNN과 유사하면서도 더 효율적이라는 것을 경험적으로 발견했다. 따라서 전체적으로 2D CNN을 사용한다. 3D 입력 $V$에 대해 2D CNN을 사용하기 위해 채널 차원을 따라 $V$의 수직 축을 연결하고 인코더에 공급한다. 또한 높은 분산의 latent space를 피하기 위해 latent 정규화를 추가한다. 1D 벡터 $g$의 경우 reparameterization trick을 통해 작은 KL-penalty를 사용하고 $c$와 $f$의 경우 vector-quantization layer를 적용하여 정규화한다.
CNN 디코더는 유사하게 2D CNN이며 세로축을 따라 concat된 $c$를 초기 입력으로 사용한다. 디코더는 $g$를 조건 변수로 하는 group normalization layer을 사용한다. 마지막으로 $f$를 디코더의 중간 텐서에 concat한다. Latent Decoder는 재구성된 voxel인 $\hat{V}$를 출력한다. LAE는 이미지 reconstruction loss $||i - \hat{i}||$와 함께 voxel reconstruction loss $||V − \hat{V}||$로 학습되며, 여기서 $\hat{i} = r(V, \hat{\kappa})$이다. 이미지 reconstruction loss는 LAE 학습에만 도움이 되며 scene auto-encoder는 고정된 상태로 유지된다.
3. Hierarchical Latent Diffusion Models
Voxel 기반 scene 표현 $V$를 나타내는 latent 변수 $g$, $c$, $f$가 주어지면 생성 모델을 diffusion model을 사용하여
\[\begin{equation} p(V, g, c, f) = p(V \vert g, c, f) p(f \vert g, c) p(c \vert g) p(g) \end{equation}\]로 정의한다.
일반적으로 discrete timestep이 있는 diffusion model은 고정된 Markovian forward process $q(x_t \vert x_{t-1})$을 가지며 여기서 $q(x_0)$는 데이터 분포를 나타내고 $q(x_T)$는 표준 정규 분포에 가까운 것으로 정의된다. 그런 다음 diffusion model은 학습 가능한 파라미터 $\theta$를 사용하여 forward process $p_\theta (x_{t-1} \vert x_t)$를 되돌리는 방법을 학습한다. Reverse process를 학습하는 것은 다음과 같은 loss을 줄임으로써 모든 timestep $t$에 대해 $x_t$에서 $x_0$로 denoise하는 방법을 학습하는 것과 같다.
\[\begin{equation} \mathbb{E}_{t, \epsilon, x_0} [w(\lambda_t) \| x_0 - \hat{x}_\theta (x_t, t) \|_2^2 ] \end{equation}\]여기서 $t$는 timestep에 대한 균일 분포에서 샘플링되고, $\epsilon$는 표준 정규 분포에서 샘플링된다. $w(\lambda_t)$는 가중치 상수이며, $\hat{x}_\theta$는 학습된 diffusion model을 나타낸다.
계층적 LDM을 다음과 같은 loss로 학습시킨다.
\[\begin{aligned} &\mathbb{E}_{t, \epsilon, g_0} [w(\lambda_t) \| g_0 - \psi_g (g_t, t) \|_2^2 ] \\ &\mathbb{E}_{t, \epsilon, g_0, c_0} [w(\lambda_t) \| c_0 - \psi_c (c_t, g_0, t) \|_2^2 ] \\ &\mathbb{E}_{t, \epsilon, g_0, c_0, f_0} [w(\lambda_t) \| f_0 - \psi_f (f_t, g_0, c_0, t) \|_2^2 ] \end{aligned}\]여기서 $\psi$는 $g$, $c$, $f$에 대한 학습 가능한 diffusion model이다.
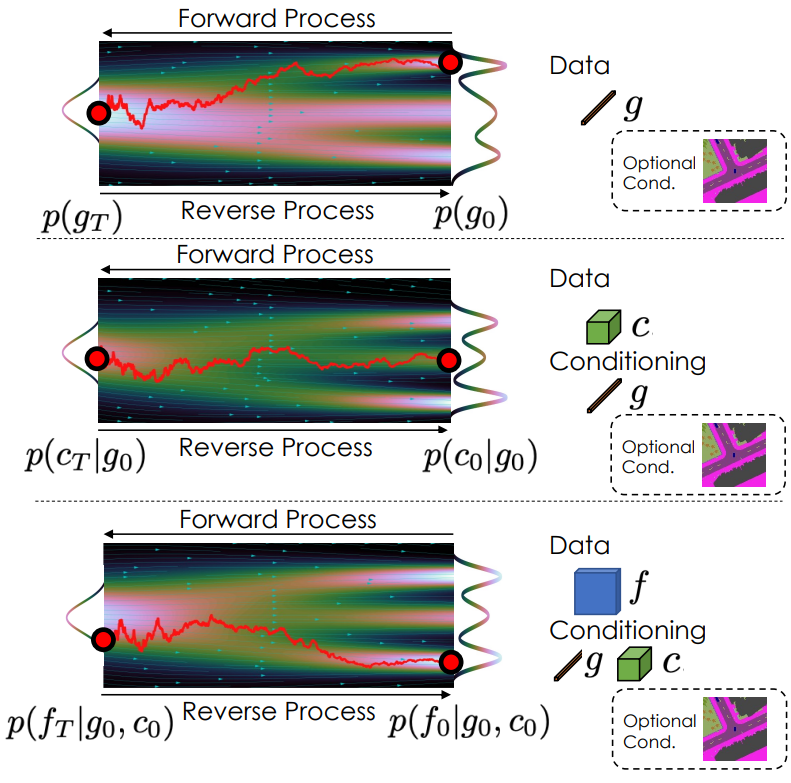
위 그림은 diffusion model을 시각화한 것이다. $\psi_g$는 skip connection이 있는 linear layer로 구현되고 $\psi_c$와 $\psi_f$는 U-net 아키텍처를 채택한다. $g$는 조건부 group normalization layer와 함께 $\psi_c$와 $\psi_f$에 공급된다. $c$는 interpolate되고 $\psi_f$에 대한 입력에 concat된다. 카메라 포즈는 카메라가 이동하는 궤적을 포함하며, 이 정보는 생성에 집중해야 하는 위치를 모델에 알려주므로 3D scene을 모델링하는 데 유용할 수 있다. 따라서 카메라 궤적 정보를 $g$에 concat하고 샘플링하는 방법도 학습한다. 조건부 생성의 경우 각 $\psi$는 조건 변수를 cross attention layer의 입력으로 사용한다.
각 $\psi$는 병렬로 학습될 수 있으며 일단 학습되면 계층 구조에 따라 하나씩 샘플링할 수 있다. 실제로는 더 나은 수렴 및 학습 안정성이 있는 것으로 나타난 $v$-prediction parameterization을 사용한다. $g$, $c$, $f$가 샘플링되면 auto-decoder를 사용하여 샘플링된 scene의 neural field를 나타내는 voxel $V$를 구성할 수 있다. 볼륨 렌더링 및 디코딩 step에 따라 샘플링된 scene을 원하는 관점에서 시각화할 수 있다.
4. Post-Optimizing Generated Neural Fields
실제 데이터에 대한 모델에서 생성된 샘플에는 합리적인 질감과 형상이 포함되어 있지만 훨씬 더 많은 데이터에 대해 학습된 2D 이미지 diffusion model의 최근 발전을 활용하여 더욱 최적화할 수 있다. 구체적으로 scene에서 viewpoint를 렌더링하고 각 이미지에 개별적으로 Score Distillation Sampling (SDS) loss를 적용하여 처음에 생성된 voxel $V$를 반복적으로 업데이트한다.
\[\begin{equation} \nabla_V L_{SDS} = \mathbb{E}_{\epsilon, t, \kappa} \bigg[ w(\lambda_t) (\epsilon - \hat{\epsilon}_\theta (r(V, \kappa), t)) \frac{\partial r(V, \kappa)}{\partial V} \bigg] \end{equation}\]여기서 $\kappa$는 수직축을 기준으로 랜덤 회전하는 scene의 원점 주변 $6m^2$ 영역에서 균일하게 샘플링된다. $w(\lambda_t)$는 \(\hat{\epsilon}_\theta\)를 학습시키는 데 사용되는 가중치 schedule이고, $t \sim U[0.02T, 0.2T]$이다. 여기서 $T$는 \(\hat{\epsilon}_\theta\)를 학습시키는 데 사용되는 noise step의 양이다.
LDM의 경우 $r(V, \kappa)$를 LDM의 latent space에 인코딩한 후 noise 예측 step이 적용되고 편미분 항이 적절하게 업데이트된다. \(\hat{\epsilon}_\theta\)의 경우 CLIP 이미지 임베딩 조건에 맞게 finetuning된 LDM을 사용한다. 모델 샘플의 CLIP 이미지 임베딩을 컨디셔닝하는 동안 이미지의 noise를 제거하면 유사한 형상 왜곡 및 텍스처 오류가 있는 이미지가 생성된다. Negative guidance로 $L_{SDS}$를 최적화하여 이 속성을 활용한다. $y$, $y’$를 각각 데이터셋 이미지 컨디셔닝와 아티팩트 컨디셔닝(ex. 샘플)의 CLIP 임베딩으로 두면, 컨디셔닝 벡터 $y$로 classifier-free guidance를 수행하지만 unconditional 임베딩을 $y’$로 바꾼다. 이는 각 denoising step에서
\[\begin{equation} \frac{p(x \vert y)^\alpha}{p(x \vert y')} \end{equation}\]에서 샘플링하는 것과 동일하며, 여기서 $\alpha$는 데이터셋 이미지에 대한 샘플링과 아티팩트가 있는 이미지에 대한 샘플링 사이의 trade-off를 제어한다. 이 사후 최적화가 voxel 샘플에 포함된 prior의 강력한 scene으로 인해 성공적이다.
Experiments

- 데이터셋: VizDoom(왼쪽 위), Replica(오른쪽 위), Carla(중간), AVD(아래)
1. Baseline Comparisons
Unconditional Generation
다음은 VizDoom과 Replica에서의 FID이다.
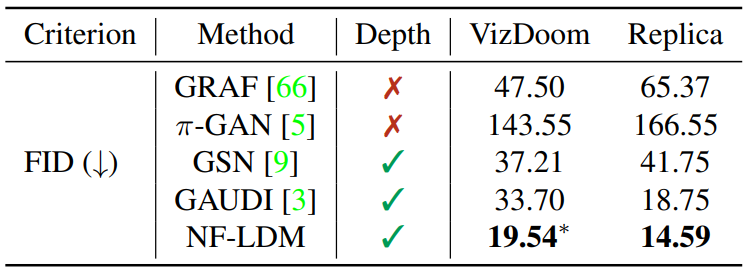
다음은 Carla와 AVD에서의 FID이다.
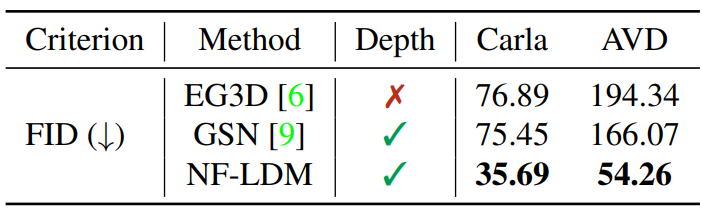
다음은 Carla(위)와 AVD(아래)에서 학습된 모델이 생성한 scene을 비교한 것이다.

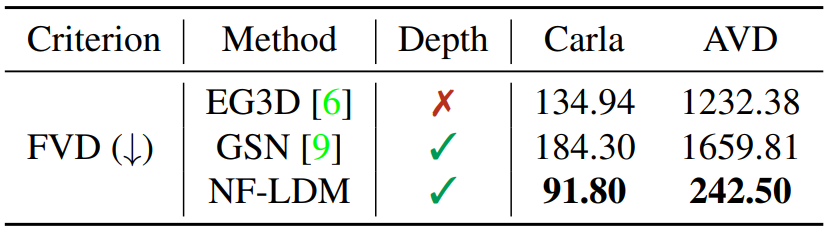
다음은 Carla와 AVD에서의 FVD이다.
다음은 density voxel에서 marching-cubes를 실행하여 NF-LDM 샘플의 형상을 시각화한 것이다.
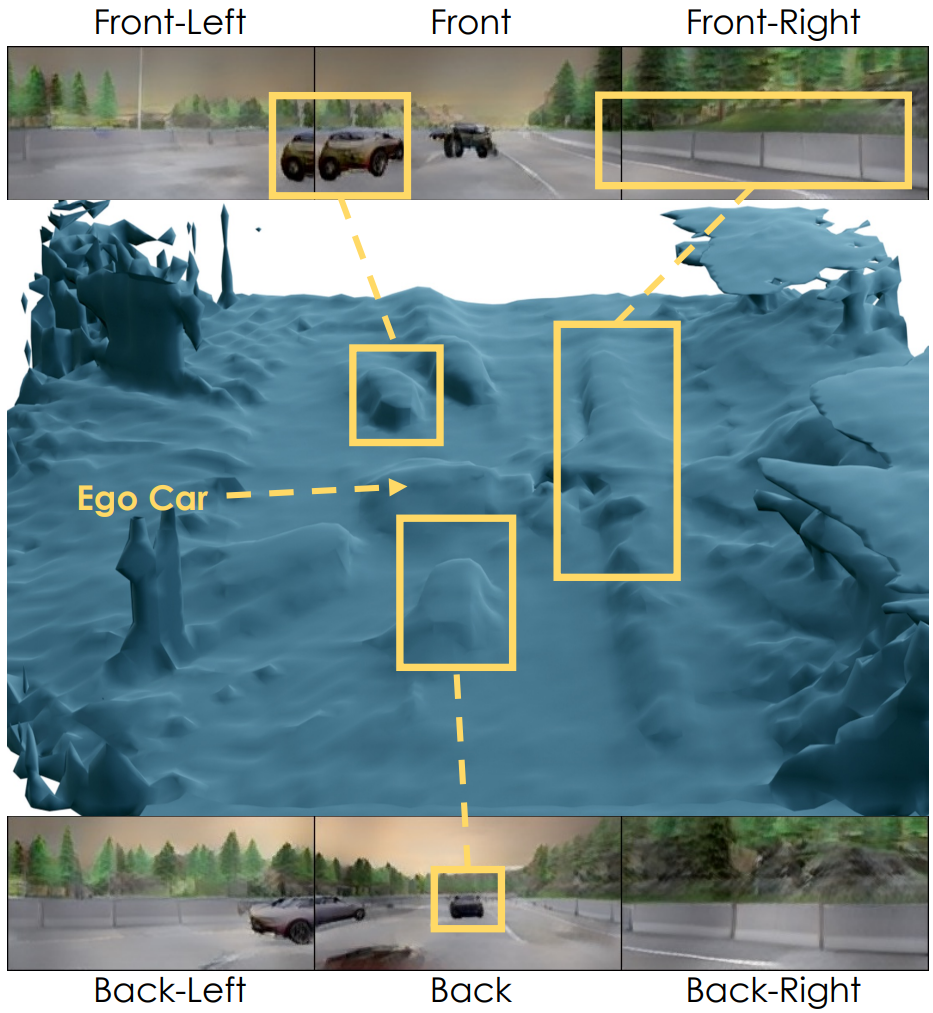
샘플이 거칠지만 사실적인 형상을 생성함을 보여준다.
Ablations
다음은 계층의 선택에 대한 ablation study 결과이다. (Carla 데이터셋)

Scene Reconstruction
다음은 학습 중에 모델이 보지 못한 scene에 대한 reconstruction 결과이다.

2. Applications
다음은 BEV segmentation map을 편집하여 생성을 제어하는 예시이다.

다음은 NF-LDM의 샘플들로 만든 파노라마이다.

다음은 3D coarse latent $c$를 사용하여 scene 편집을 한 예시이다.

3. Limitations
NF-LDM의 계층적 구조와 3단계 파이프라인을 통해 고품질 생성 및 재구성을 달성할 수 있지만 학습 시간과 샘플링 속도가 저하된다. 본 논문에서 neural field 표현은 조밀한 voxel grid를 기반으로 하며 볼륨이 커질수록 diffusion model을 학습하고 볼륨을 렌더링하는 데 비용이 많이 든다. 또한 본 논문의 방법은 데이터 가용성을 제한하는 multi-view 이미지가 필요하므로 overfitting 문제가 발생할 위험이 있다. 데이터셋 자체가 제한된 수의 scene에 기록되었기 때문에 AVD의 출력 샘플에는 다양성이 제한되어 있다.