[논문리뷰] Nexels: Neurally-Textured Surfels for Real-Time Novel View Synthesis with Sparse Geometries

arXiv 2025. [Paper] [Page] [Github]
Victor Rong, Jan Held, Victor Chu, Daniel Rebain, Marc Van Droogenbroeck, Kiriakos N. Kutulakos, Andrea Tagliasacchi, David B. Lindell
University of Toronto | Vector Institute | Simon Frasier University | University of Liège | University of British Columbia
15 Dec 2025

Introduction

3D Gaussian Splatting (3DGS)은 각 primitive가 geometry와 외형을 동시에 인코딩한다. 이러한 결합은 coarse한 geometry (ex. 사각형)에서도 텍스처링을 통해 세밀한 외형을 표현할 수 있는 기존의 표면 기반 방식과 대조적이다. Gaussian splat은 디테일한 외형을 표현하기 위해 많은 수의 primitive를 필요로 하므로 상당한 메모리 사용량을 초래한다.

Geometry와 외형을 분리함으로써 더욱 간결한 표현이 가능해진다. 외형을 텍스처에 맡기면 메쉬 기반 모델은 매우 사실적인 장면을 묘사할 수 있다. 그러나 메쉬는 3D 장면의 입력 이미지 모음에서 새로운 시점을 생성하는 novel view synthesis에서는 뒤처져 왔다. 메쉬는 discrete한 연결성, 자기 교차 가능성, 윤곽선 gradient 계산의 복잡성으로 인해 미분 가능한 렌더링 시에 어려움을 겪는다.

메쉬 최적화의 복잡성 없이 과도한 수의 primitive 사용 필요성을 완화하기 위해, 최근 연구에서는 텍스처가 적용된 splat을 도입하여 Gaussian Splatting에서 geometry와 외형을 분리하는 방식을 제안했다. 이는 일반적으로 primitive별 이미지 텍스처를 사용하는 방식이다. 그러나 해상도에 따라 메모리 사용량이 제곱으로 증가하므로 대규모 장면에서 디테일한 외형을 표현하는 데 제약이 있다. 신경망을 이용하여 외형을 지연 처리하는 방식은 해시 그리드 조회에서 상당한 비용이 소요되며, 모든 ray-primitive 교차점에 대해 여러 번 조회하면 렌더링 속도와 학습 속도가 모두 느려진다.

이러한 방법들은 표준 메쉬 rasterization 방식에서는 불투명한 표면 조각의 일부에 대해서만 텍스처 계산이 수행된다는 점을 간과하고 있다. 이러한 점에 착안하여, 본 논문에서는 실시간 렌더링 성능 저하 없이, 포인트 기반 접근 방식의 최적화 이점을 유지하면서 메쉬 기반 방식의 가벼운 외형 모델링을 활용하는 새로운 표현 방식인 nexel을 제안하였다.

구체적으로, geometry 측면에서는 미분 가능한 quad indicator를 도입하여 표면과 날카로운 경계를 더욱 정확하게 재구성할 수 있도록 했다. 외형 측면에서는 world-space neural field를 학습시켜 가장 관련성이 높은 primitive에만 텍스처를 제공함으로써, 계산량을 낮추면서도 미세한 디테일을 효율적으로 포착하였다. 기존의 텍스처링 방식과 비교했을 때, nexel은 두 배 이상 빠른 렌더링 속도를 유지하면서 더 나은 렌더링 품질을 제공한다.

Method

1. Representation

Geometry

Nexel의 geometry는 불투명도를 조절하는 커널로 정의된 $N$개의 surfel 집합을 사용하여 표현된다. 2DGS에 따라, $i$번째 primitive는 평균 \(\mu_i \in \mathbb{R}^3\), rotation \(R_i \in \mathbb{SO}_3\), scale \(\sigma_i \in \mathbb{R}^2\), 불투명도 $o_i \in \mathbb{R}$을 가진다. 또한, primitive가 얼마나 직사각형에 가까운지를 조절하는 감마 파라미터 \(\gamma_i \in \mathbb{R}^2\)이 있다. $\gamma$ 값은 항상 1보다 크거나 같다.

Primitive space에서 교차점 $(u, v)$에서의 불투명도는 일반화된 Gaussian 분포로 정의된다.

\[\begin{equation} \alpha = o_i \exp \left( - \frac{\vert u \vert^{2 \gamma_{i,1}}}{2} \right) \left( - \frac{\vert v \vert^{2 \gamma_{i,2}}}{2} \right) \end{equation}\]

위 그림은 $\gamma$ 값에 따른 nexel 모양을 보여준다. $\gamma \rightarrow 1$일 때, 커널은 Gaussian 분포로 수렴한다. $\gamma \rightarrow \infty$일 때는 급격한 경계를 가진 사각형으로 수렴한다. 이 커널은 불투명하고 평평한 표면을 모델링하는 데 적합하다. $o$와 $\gamma$ 값이 클 때, 함수는 대부분의 영역에서 1에 가까운 값을 유지하는데, 이는 긴 꼬리를 가지는 기존 Gaussian과는 대조적이다. 따라서 커널은 부드러움이 필요한 영역에서는 Gaussian처럼 동작하면서도, 급격한 경계가 필요한 영역에서는 선명한 가장자리를 생성할 수 있다.

Appearance

각 surfel은 텍스처가 없는 모드와 텍스처가 있는 모드, 두 가지 외형 모드를 가지고 있다. 렌더링 과정에서 픽셀 단위로 사용할 모드를 선택한다. Surfel $i$의 텍스처가 없는 외관은 2DGS와 동일하며, \(c_i^\odot \in \mathbb{R}^{3S}\)이다.

각 primitive의 텍스처가 있는 외형은 Instant-NGP 아키텍처를 기반으로 하는 공유 neural field $\mathcal{F}$를 사용하여 표현된다. 이 neural field는 임의의 3D 위치 $x \in \mathbb{R}^3$를 입력으로 받아 시점에 따라 달라지는 radiance $\mathcal{F} (x)$를 spherical harmonics 계수 집합으로 출력한다. Surfel의 특정 지점에서의 텍스처는 해당 위치의 neural field를 조회함으로써 계산할 수 있다.

Primitive $i$에 대해, $t_i^\ast (r)$을 교차점의 깊이로, $x_i^\ast (r) = o + t^\ast d$를 world-space 교차점으로 정의하자. 단순하게 생각하면, 픽셀 $p$의 텍스처링된 외형은 \(\mathcal{F}(x_i^\ast (r))\)이 된다. 미분 가능한 렌더링에 포인트 샘플을 사용하면 해시 그리드의 fine한 레벨에서 정확도가 떨어진다. Zip-NeRF의 down-weighting 분석에 따라, 레벨 $\ell$의 해시 그리드 feature에 \(\Delta_{i,\ell} (r)\)을 곱한다.

\[\begin{equation} \Delta_{i,\ell} (r) = 1 - \exp \left( - \frac{1}{2 \pi} \left( \frac{f}{s_\ell t_i^\ast (r)} \right)^2 \right) \end{equation}\]

($f$는 focal length)

이는 단순 샘플링과 동일한 계산량을 요구하며 눈에 띄는 앨리어싱 아티팩트를 제거한다. 최종적으로, primitive $i$에 대한 $r$을 따라 필터링된 텍스처 radiance는 다음과 같이 정의된다.

\[\begin{equation} c_i^\oplus (r) = \mathcal{G} (\Delta_i (r) \cdot \mathcal{H} (x_i^\ast (r))) \end{equation}\]

($\mathcal{G}$는 MLP, $\mathcal{H}$는 해시 그리드)

\(c_i^\oplus (r)\)을 계산하는 데 필요한 유일한 primitive 정보는 교차 깊이 $t_i^\ast (r)$이다.

2. Rendering

렌더링 단계는 이미지 픽셀에 대한 두 번의 pass로 구성된다. 첫 번째 pass에서는 텍스처가 적용되지 않은 외형만을 사용하여 초기 렌더링을 계산하고 텍스처를 적용해야 하는 primitive에 대한 정보를 수집한다. 두 번째 패스에서는 수집된 ray-primitive 교차점에 신경망 텍스처를 적용하고 초기 렌더링을 업데이트한다.

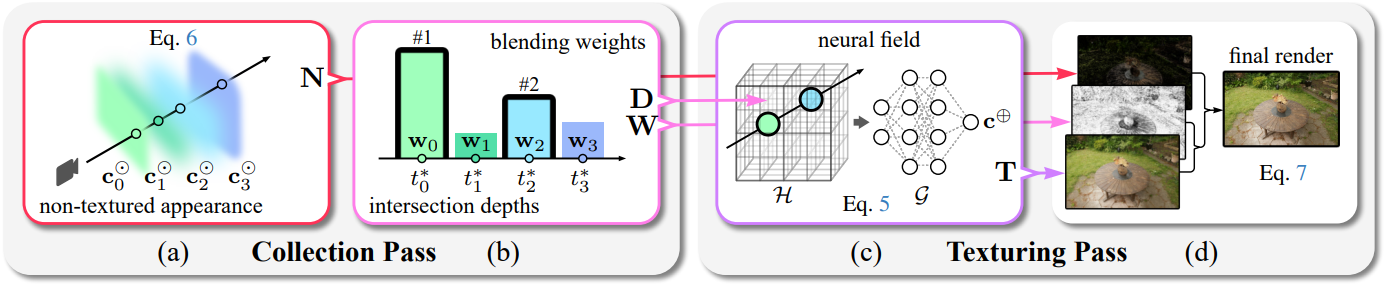
Collection Pass

첫 번째 패스에서 픽셀 광선과 교차하는 $M$개의 surfel을 가로질러 알파 \(\alpha_i\)와 투과율 $T_i$를 계산한다. 텍스처링된 primitive가 없다고 가정하고 각 픽셀에 대한 초기 렌더링 $\textbf{N}$을 계산한다.

하나의 픽셀을 렌더링할 때, 텍스처링되는 primitive의 개수를 hyperparameter $K \ll M$으로 제한한다. 텍스처링되는 primitive의 부분집합은 블렌딩 가중치 \(w_i = \alpha_i T_i\)를 기반으로 결정한다. 주어진 픽셀에 대해 가중치가 가장 높은 $K$개의 primitive를 선택한다. Fragment buffer 기법에서 영감을 받아, 픽셀 단위로 크기 $K$의 buffer를 유지한다. 각 buffer entry에는 primitive의 ID, 가중치, 깊이가 저장되며, 총 $3K$개의 32-bit 레지스터를 사용한다. 초기에는 buffer가 비어 있다. $M$개의 primitive를 순회하며 가중치를 계산할 때, buffer를 업데이트하여 가중치가 가장 높은 primitive를 저장한다. 최종 ID, 깊이, 가중치 buffer는 각각 $H \times W \times K$ 크기의 이미지 $\textbf{I}$, $\textbf{D}$, $\textbf{W}$에 기록된다. 이 값들은 텍스처가 적용되지 않은 렌더링 결과 $\textbf{N}$과 함께 반환된다. 또한, $\textbf{I}$에 있는 $K$개의 primitive에 대해서는 렌더링 결과 $\textbf{N}$에서 색상을 제거한다. 픽셀 $p$에서의 텍스처가 적용되지 않은 렌더링 결과의 최종 값은 다음과 같다.

\[\begin{equation} \textbf{N}_p = \sum_{i=0}^{M-1} [i \notin \textbf{I}_p] w_i c_i^\odot \end{equation}\]

Texturing Pass

텍스처링 단계에서는 먼저 depth buffer $\textbf{D}$에서 world-space 교차점 위치를 계산하여 $x \in \mathbb{R}^{H \times W \times K \times 3}$을 얻는다. 그런 다음, 신경망에 쿼리하여 필터링된 텍스처 $\textbf{T} \in \mathbb{R}^{H \times W \times K \times 3}$을 계산한다. 최종 렌더링 결과는 다음과 같다.

\[\begin{aligned} \sum_{i=0}^{M-1} T_i \alpha_i c_i (r) &= \sum_{i=0}^{M-1} w_i ([i \notin \textbf{I}_p] c_i^\odot + [i \in \textbf{I}_p] c_i^\oplus (r)) \\ &= \textbf{N}_p + \sum_{j=0}^{K-1} \textbf{W}_{p,j} \textbf{T}_{p,j} \end{aligned}\]

3. Optimization

본 논문에서는 3DGS 방식을 따르고 정규화를 적용하여 3만 iteration에 대해 최적화를 수행한다. 또한 density control 연산을 중간중간에 삽입하였다.

Adaptive Density Control

본 논문에서는 primitive의 개수를 제어하는 hyperparameter $P$를 도입하였다. BBSplat과 유사하게, 초기화를 위해 COLMAP의 포인트 클라우드 출력을 샘플링한다. 구체적으로, farthest point sampling을 사용하여 초기 포인트 클라우드를 $P/2$개로 줄인다. 샘플링 과정에서 각 포인트의 scale은 이전 포인트와의 거리를 기준으로 초기화된다.

또한 불필요한 primitive를 제거하고 현재 geometry가 불충분한 영역에 새로운 primitive를 추가한다. 500번째 iteration부터 25,000번째 iteration까지 100 iteration마다 densification과 pruning 단계를 수행한다. Primitive의 5%를 선택하여 가장 긴 축을 따라 균등하게 분할한다. 이 선택은 Revising Densification in Gaussian Splatting의 방법과 유사하게 혼합 오차를 사용하여 정의된 확률에 따라 이루어진다. 분할 시 추가되는 primitive의 개수는 $P$로 제한된다. 그 후, 불투명도가 0.005 미만인 모든 primitive를 제거한다.

Losses

각 iteration에서, 주어진 학습 뷰의 nexel들을 렌더링하여 예측 이미지를 생성한다. 3DGS와 동일한 photometric loss를 사용한다.

\[\begin{equation} \mathcal{L}_\textrm{image} = (1 - \lambda_\textrm{D-SSIM}) \mathcal{L}_1 + \lambda_\textrm{D-SSIM} \mathcal{L}_\textrm{D-SSIM} \end{equation}\]

(\(\lambda_\textrm{D-SSIM} = 0.2\))

또한, 텍스처가 GT 이미지 $I^\textrm{GT}$에 맞도록 텍스처 loss \(\mathcal{L}_\textrm{texture}\)를 사용한다.

\[\begin{equation} \mathcal{L}_\textrm{texture} = \frac{1}{3HW} \sum_{y=0}^{H-1} \sum_{x=0}^{W-1} \sum_{c=0}^2 \left\vert I_{y,x,c}^\textrm{GT} - \frac{\sum_{j=0}^{K-1} \textbf{W}_{y,x,j} \textbf{T}_{y,x,j,c}}{\sum_{j=0}^{K-1} \textbf{W}_{y,x,j}} \right\vert \end{equation}\]

텍스처가 적용되지 않은 렌더링에 불이익을 주기 위해, 텍스처가 적용되지 않은 외형의 전체 블렌딩 가중치를 최소화한다.

\[\begin{equation} \mathcal{L}_\textrm{alpha} = \frac{1}{HW} \sum_{y=0}^{H-1} \sum_{x=0}^{W-1} \left( 1 - \sum_{j=0}^{K-1} \textbf{W}_{y,x,j} \right) \end{equation}\]

Sparsity를 유도하기 위해 불투명도에 $L_1$ loss를 적용한다.

\[\begin{equation} \mathcal{L}_\textrm{opacity} = \frac{1}{N} \sum_{i=0}^{N-1} o_i \end{equation}\]

그리드 안티앨리어싱에 대한 가중치 감소를 정당화하기 위해 그리드 평균값이 0에 가깝도록 하는 그리드 가중치 정규화 항을 추가한다.

\[\begin{equation} \mathcal{L}_\textrm{grid} = \sum_{\ell = 0}^{L-1} \sum_{i=0}^{T-1} \sum_{j=0}^{F-1} s_i^{-3} \mathcal{H}_{\ell, i, j} \end{equation}\]

최종 loss는 다음과 같다.

\[\begin{aligned} \mathcal{L} = \mathcal{L}_\textrm{image} &+ \lambda_\textrm{alpha} \mathcal{L}_\textrm{alpha} + \lambda_\textrm{texture} \mathcal{L}_\textrm{texture} \\ &+ \lambda_\textrm{opacity} \mathcal{L}_\textrm{opacity} + \lambda_\textrm{grid} \mathcal{L}_\textrm{grid} \end{aligned}\]

(\(\lambda_\textrm{alpha} = 0.005\), \(\lambda_\textrm{texture} = 0.5\), \(\lambda_\textrm{opacity} = 0.01\), \(\lambda_\textrm{grid} = 0.01\))

Experiments

1. Evaluation

다음은 렌더링 품질을 비교한 결과이다.

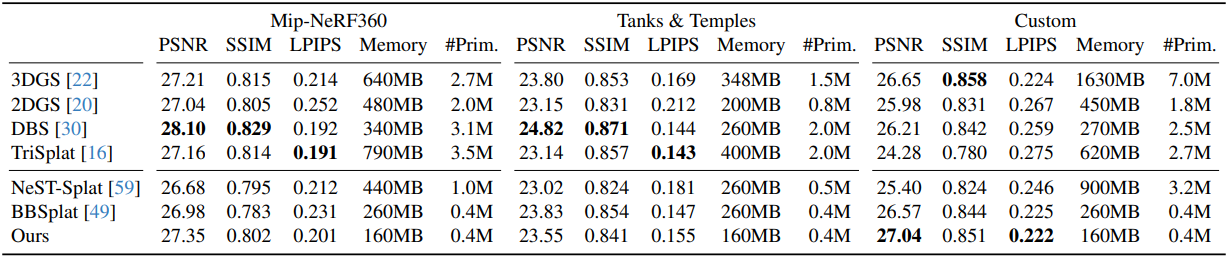
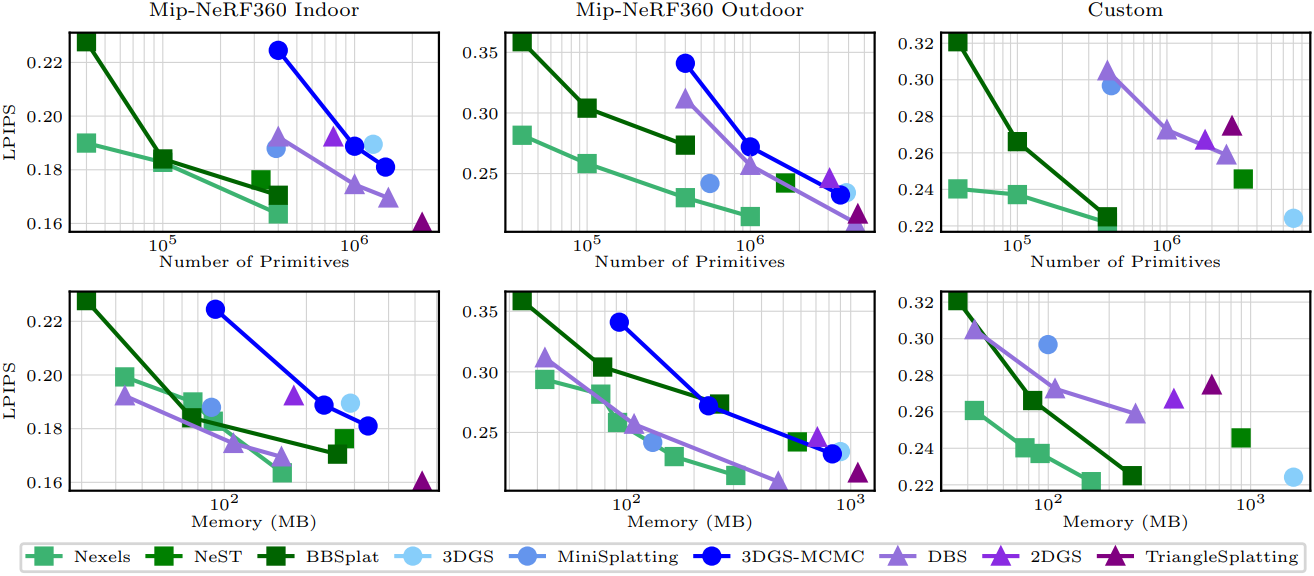
다음은 sparse한 geometry에 대한 비교 결과이다.

다음은 낮은 메모리 세팅에서의 비교 결과이다.

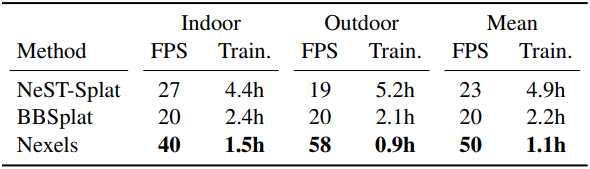
다음은 학습 시간과 렌더링 속도를 비교한 결과이다.

2. Ablations

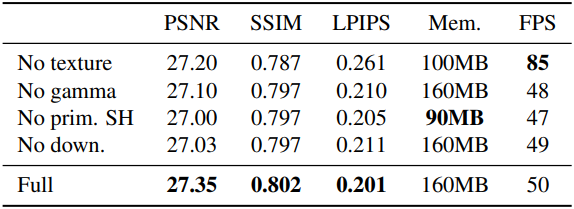
다음은 ablation 결과이다.

Limitations

1. Instant-NGP 모델의 속도는 고성능 GPU에서만 사용 가능한 텐서 코어 연산에 의존한다.
2. Nexel은 보이지 않는 영역에서 노이즈를 발생시키는데, 이는 Gaussian splat으로 인한 흐릿한 아티팩트보다 덜 매력적일 수 있다.
3. 모션 블러와 같은 이미지 처리의 모든 복잡성을 지원하지 않는다.