[논문리뷰] NeuSG: Neural Implicit Surface Reconstruction with 3D Gaussian Splatting Guidance
arXiv 2023. [Paper]
Hanlin Chen, Chen Li, Gim Hee Lee
National University of Singapore
1 Dec 2023
Introduction
여러 뷰에서 표면을 재구성하는 것은 3D 컴퓨터 비전의 fundamental task이다. 기존의 접근 방식은 multi-view stereo(MVS) 기술을 통해 이미지로부터 포인트 클라우드를 추정한 다음 포인트 클라우드에서 삼각형 메쉬를 추출하는 것이다. 최근에는 implicit한 뉴럴 표면 재구성이 경쟁력 있는 대안으로 등장했으며, 특히 텍스처가 제한적이고 non-Lambertian인 표면에 효과적이다. 이러한 방법은 MLP 또는 해시 인코딩을 사용하여 밀도, occupancy, 또는 가장 가까운 표면 지점까지의 signed distance와 같은 기하학적 속성을 공간 좌표에 할당한다.
뉴럴 표면 재구성에 signed distance function(SDF)을 적용하는 것은 특히 주목할 만하다. 이는 SDF로 유도된 밀도 함수의 사용을 포함하므로 볼륨 렌더링이 implicit한 SDF 표현을 학습할 수 있다. 렌더링 감독만 사용하는 현재의 implicit한 방법들은 단순한 장면에 대해 인상적인 결과를 생성하지만, 더 큰 장면, 특히 텍스처가 없는 광범위한 영역이 포함된 장면에서는 문제에 직면한다. 이전 연구들에서는 depth prior, normal regularization 등과 같은 구조적 prior를 최적화 프로세스에 통합하여 이 문제를 해결하려고 시도했다. 이러한 방법들은 완전한 표면을 재구성하는 데 성공하지만 세밀한 디테일이 부족하고 표면이 과도하게 부드러워지는 경우가 많다. 특히, 몇몇 연구에서는 표면 재구성의 충실도를 향상시키기 위해 MVS의 포인트 클라우드를 활용하였다. 그럼에도 불구하고 MVS에서 예측된 포인트 클라우드는 균일하게 분포되어 있고 때로는 불완전하므로 일부 지역, 특히 복잡한 디테일이 있는 지역에 대한 geometric prior를 제공하지 못한다. 또한, 생성된 점들은 필연적으로 신뢰할 수 없는 잡음이 많은 기하학적 구조로 인해 어려움을 겪는다.
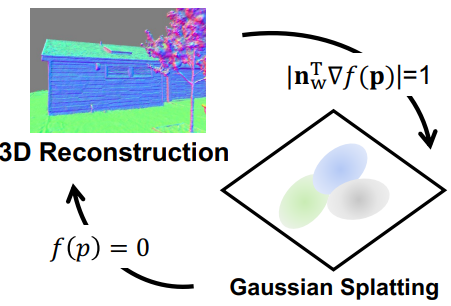
3D Gaussian Splatting의 장점은 상세한 기하학적 구조로 dense한 포인트 클라우드를 생성할 수 있다는 것이다. 이는 특히 복잡한 디테일이 있는 영역에 충분한 기하학적 제약 조건을 제공한다. 그러나 바닐라 3D Gaussian Splatting으로 생성된 포인트 클라우드는 일반적으로 표면 내부에 위치하는 3D Gaussian의 중심으로 계산되므로 prior로 직접 사용할 수 없다. 이를 위해 점을 표면에 가깝게 만드는 scale regularizer를 도입한다. 특히, 3D Gaussian 타원체가 평면이 되도록 각 3D Gaussian의 가장 작은 scale factor를 0에 가깝게 적용한다. 그러면 정확한 색상을 렌더링하기 위해 매우 얇은 3D Gaussian이 표면으로 이동된다.
기존 포인트 클라우드 기반 접근 방식과 유사하게 3D Gaussian Splatting에서 생성된 포인트 클라우드는 잡음이 많으므로 잘못된 prior를 제공할 수 있다. 이 문제를 완화하기 위해 본 논문은 neural implicit model인 NeuS에 의해 예측된 표면의 normal prior로 3D Gaussian을 개선하는 것을 추가로 제안하였다. 구체적으로, 3D Gaussian 타원체는 평면에 가깝기 때문에 scaling factor가 가장 작은 방향을 normal 방향으로 간주할 수 있다. NeuS가 예측한 normal과 정렬하여 normal 방향을 정규화한다. 이러한 공동 최적화를 통해 3D Gaussian에서 생성된 포인트 클라우드는 보다 안정적인 prior를 제공하도록 개선된다. 결과적으로 본 논문의 접근 방식은 두 가지 표현의 이점을 모두 활용하고 복잡한 디테일이 포함된 완전한 표면을 생성할 수 있다.
Method
1. Preliminary
NeRF는 볼륨 렌더링을 통해 새로운 뷰를 합성하기 위해 밀도 및 색상 필드를 사용하여 3D 장면을 캡처한다. 이 방법은 투명한 표면을 정의하는 데 어려움을 겪으며 밀도에서 파생될 때 종종 잡음이 많고 비현실적인 표면이 생성된다. Signed distance function(SDF)은 implicit하게 표면을 zero-level set \(\{\textbf{x} \in \mathbb{R}^R 3 \, \| \, f(\textbf{x}) = 0\}\)으로 표현한다. 여기서 $f(\textbf{x})$는 MLP $f(\cdot)$의 SDF 값이다. NeuS는 NeRF의 볼륨 밀도 출력을 SDF로 대체한다. 학습은 불가능하지만 미분 가능한 logistic function은 볼륨 렌더링을 위해 SDF를 불투명도로 변환하도록 설계된다. 결과적으로 중간 SDF 출력은 Eikonal regularization을 통해 표면 재구성의 품질을 향상시킨다. SDF 값이 \(f(\textbf{x}_i)\)인 3D 점 \(\textbf{x}_i\)에 대한 불투명도 $\alpha_i$는 다음과 같다.
\[\begin{equation} \alpha_i = \max \bigg( \frac{\Phi_s (f (\textbf{x}_i)) - \Phi_s (f (\textbf{x}_{i+1}))}{\Phi_s (f (\textbf{x}_i))}, 0 \bigg) \end{equation}\]여기서 $\Phi_s$는 sigmoid function이다. $\textbf{o}$에 위치한 카메라와 광선 방향 $\textbf{d}$가 주어지면 이 불투명도는 볼륨 렌더링 프로세스에서 광선을 따라 색상을 통합하는 데 사용된다. 각 점 \(\textbf{c}_i\)의 색상은 MLP에 의해 예측되며, 픽셀의 색상은 색상 값의 리만 합이다.
\[\begin{equation} \hat{\textbf{C}}(\textbf{o}, \textbf{d}) = \sum_{i=1}^N w_i \textbf{c}_i, \quad \textrm{where} \; w_i = T_i \alpha_i \end{equation}\]여기서 $T_i$는 카메라에 도달하는 빛의 비율을 나타내는 누적 투과율이며 $N$은 광선에 있는 샘플 점의 수이다.
2. 3D Gaussian Splatting
3D Gaussian Splatting은 3D Gaussian으로 3D 장면을 표현하는 방법이다. 각 Gaussian은 공분산 행렬 $\boldsymbol{\Sigma}$와 평균인 중심점 $\textbf{p}$로 정의된다. 3D Gaussian은 다음과 같이 나타낼 수 있다.
\[\begin{equation} G(\textbf{x}) = \exp (-\frac{1}{2} (\textbf{x} - \textbf{p})^\top \boldsymbol{\Sigma}^{-1} (\textbf{x} - \textbf{p})) \end{equation}\]최적화를 위해 공분산 행렬 $\boldsymbol{\Sigma}$는 scaling matrix $\textbf{S}$와 rotation matrix $\textbf{R}$의 곱으로 표현된다.
\[\begin{equation} \boldsymbol{\Sigma} = \textbf{R} \textbf{S} \textbf{S}^\top \textbf{R}^\top \end{equation}\]$\textbf{S}$는 scaling factor $\textbf{s}$에 의해 저장된 대각 행렬이다. Rotation matrix $\textbf{R}$은 quaternion $\textbf{r} \in \mathbb{R}^4$로 표현된다.
새로운 뷰 렌더링을 위해 splatting 기술이 카메라 평면의 Gaussian에 적용된다. Viewing transform $\textbf{W}$와 projective transformation의 affine 근사의 Jacobian $\textbf{J}$를 사용하여 변환된 공분산 행렬 $\boldsymbol{\Sigma}^\prime$은 다음과 같다.
\[\begin{equation} \boldsymbol{\Sigma}^\prime = \textbf{J} \textbf{W} \boldsymbol{\Sigma} \textbf{W}^\top \textbf{J}^\top \end{equation}\]완전한 3D Gaussian은 위치 $\textbf{p} \in \mathbb{R}^3$, spherical harmonics 계수 $\textbf{H} \in \mathbb{R}^k$로 표시되는 색상, 불투명도 $\alpha \in \mathbb{R}$, quaternion $\textbf{r} \in \mathbb{R}^4$, scaling factor $\textbf{s} \in \mathbb{R}^3$으로 주어진다. 주어진 픽셀에 대해 여러 Gaussian의 결합된 색상과 불투명도는 NeRF와 마찬가지로 알파-블렌딩된다. 겹치는 점의 색상 혼합은 다음과 같다.
\[\begin{equation} \textbf{C} = \sum_{i \in N} \textbf{c}_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]2. Regularization for 3D Gaussians
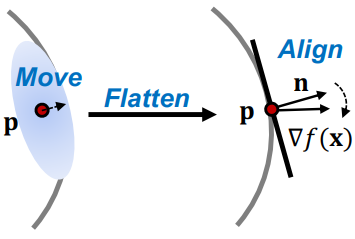
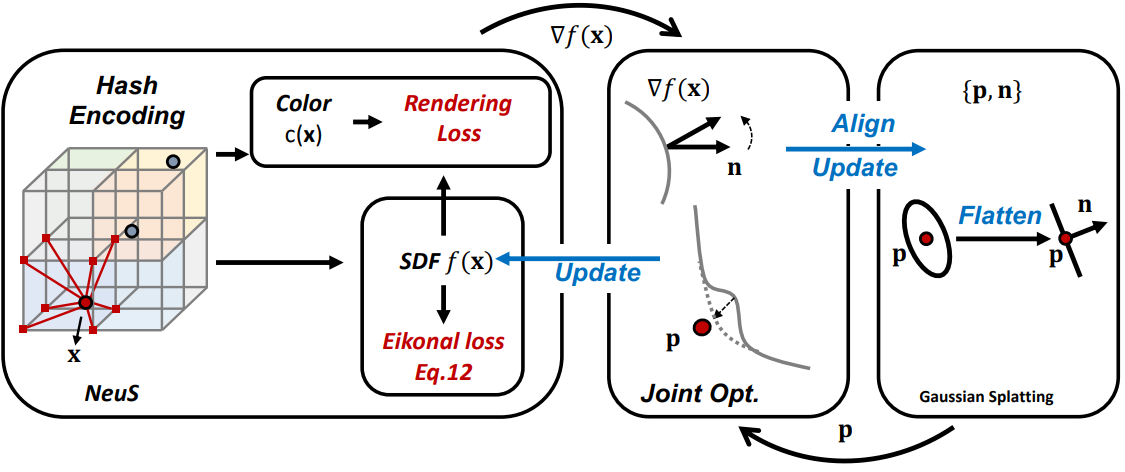
저자들은 매우 상세한 표면을 복구하기 위해 3D Gaussian Splatting의 활용을 제안하였다. 이 방법은 복잡한 디테일을 나타내는 dense한 포인트 클라우드을 만드는 데 유용하다. 그러나 3D Gaussian Splatting은 3D Gaussian의 중심이 실제 표면과 정렬되지 않을 수 있으므로 직접 적용할 수 없다. 이 문제를 피하기 위해 scale regularizer를 도입한다. 또한 3D Gaussian Splatting에서 생성된 포인트에 노이즈가 있다는 점을 고려하여 NeuS에서 예측한 normal prior를 사용하여 3D Gaussian을 개선할 것을 제안하였다. 프로세스는 위 그림과 같다.
Scale Regularization
기존의 3D Gaussian Splatting은 일반적으로 표면 내부에 위치하는 Gaussian 중심 \(\{\textbf{p}_i\}\)를 생성하므로 직접적인 표면 정규화에 적합하지 않다. 이 문제를 해결하기 위해 3D Gaussian 타원체를 매우 평평한 모양으로 다듬는다. 이 프로세스는 Gaussian이 상당히 좁아지게 하여 중심을 표면에 더 가깝게 끌어당긴다. 3D Gaussian 내에서 scaling factor $\textbf{s}$는 각 방향의 타원체 크기를 정의한다. Scaling factor를 조작하여 Gaussian의 모양을 변경할 수 있다. 구체적으로, 각 Gaussian에 대해 scaling factor $\textbf{s} = (s_1, s_2, s_3)^\top \in \mathbb{R}^3$의 가장 작은 성분을 0으로 최소화한다.
\[\begin{equation} \mathcal{L}_s = \| \min (s_1, s_2, s_3) \|_1 \end{equation}\]이 프로세스는 3D Gaussian을 효과적으로 평탄화하여 중심점 \(\{\textbf{p}_i\}\)가 표면과 정렬되도록 한다.
Normal Regularization
Gaussian이 평평해짐에 따라 가장 작은 scaling factor의 방향은 얇은 Gaussian의 normal이 된다. 카메라 좌표계에서 normal을 다음과 같이 정의한다.
\[\begin{equation} \textbf{n}_c = \textrm{OneHot} (\arg \min (s_1, s_2, s_3)) \in \mathbb{R}^3 \end{equation}\]여기서 $\textrm{OneHot}(\cdot)$은 인덱스를 벡터로 변환한다. 그런 다음 normal \(\textbf{n}_c\)는 rotation $\textbf{R}$을 사용하여 월드 좌표계로 변환된다.
\[\begin{equation} \textbf{n}_w = \textbf{R} \textbf{n}_c \end{equation}\]그런 다음 NeuS가 예측한 표면 normal과 \(\textbf{n}_w\)를 정렬하여 Gaussian을 fine-tuning한다.
\[\begin{equation} \mathcal{L}_\textrm{align} = \vert 1 - \vert \textbf{n}_w^\top \cdot \nabla f (\textbf{p}_i) \vert \vert_1 \end{equation}\]절대값은 벡터 방향에 관계없이 올바른 방향을 보장한다. 3D Gaussian에서 파생된 포인트 클라우드는 normal 정렬을 통해 개선되므로 표면 최적화를 위한 보다 신뢰할 수 있는 prior를 제공한다.
3. Joint Optimization
처음에 NeuS는 렌더링 loss, Eikonal loss, 3D Gaussian에서 파생된 포인트 클라우드에 의한 제약 조건을 포함하는 복합적인 loss function을 통해 최적화된다. 그 후, NeuS가 예측한 normal을 활용하여 3D Gaussian을 더욱 개선한다.
Implicit Surface Reconstruction
네트워크 학습은 입력 이미지 $\textbf{C}$와 렌더링된 출력 $\hat{\textbf{C}}$ 사이의 불일치를 측정하는 color loss를 기준으로 진행된다.
\[\begin{equation} \mathcal{L}_\textrm{RGB} = \| \textbf{C} - \hat{\textbf{C}} \|_1 \end{equation}\]표면 디테일을 더욱 구체화하기 위해 Eikonal 정규화 항은 3차원 공간에서 SDF의 올바른 gradient norm을 적용한다.
\[\begin{equation} \mathcal{L}_\textrm{eik} = \frac{1}{N} \sum_{i=1}^N (\| \nabla f(\textbf{x}_i) \|_2 - 1)^2 \end{equation}\]여기서 \(\nabla f(\textbf{x}_i)\)는 점 \(\textbf{x}_i\)에서 계산된 SDF \(f(\textbf{x}_i)\)의 기울기이다. 이는 SDF 기반 볼륨 렌더링을 위한 NeuS 프레임워크와 일치한다.
포인트 클라우드 \(\textbf{p}_i\)에서의 SDF 값이 0에 가까워지도록 강제하여 표면 최적화에 기여한다.
\[\begin{equation} \mathcal{L}_\textrm{pt} = \vert f (\textbf{p}_i) \vert_1 \end{equation}\]여기서 \(f(\textbf{p}_i)\)는 점 \(\textbf{p}_i\)에서 예측된 SDF 값이다. 이러한 loss들을 결합한 전체 loss function은 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{total} = \mathcal{L}_\textrm{RGB} + \lambda_1 \mathcal{L}_\textrm{eik} + \lambda_2 \mathcal{L}_\textrm{pt} \end{equation}\]여기서 $\lambda_1$와 $\lambda_2$는 각 성분의 균형을 맞춘다.
Gaussian Splatting Refinement
Color loss \(\mathcal{L}_\textrm{RGB}\) 외에도 \(\mathcal{L}_s\)를 통해 scaling factor를 최소화하고 \(\mathcal{L}_\textrm{align}\)을 통해 normal을 정렬한다. 따라서 Gaussian Splatting의 loss function은 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{Gaussian} = \mathcal{L}_\textrm{RGB} + \lambda_3 \mathcal{L}_s + \lambda_4 \mathcal{L}_\textrm{align} \end{equation}\]여기서 $\lambda_3$과 $\lambda_4$는 각각 scaling 항과 alignment 항의 가중치이다. 이러한 상호 최적화를 통해 3D Gaussian에서 생성된 포인트 클라우드가 개선되어 보다 안정적인 prior를 제공한다.
Experiments
- 데이터셋: Tanks and Temples
- 구현 디테일
- optimizer: Adam (learning rate = $10^{-3}$)
- $\lambda_1$ = 0.1, $\lambda_2$ = 1, $\lambda_3$ = 100, $\lambda_4$ = 1
- 학습 중에는 각 iteration마다 1024개의 광선을 샘플링
- NeuralAngelo에서 제안된 해시 인코딩, 멀티스케일 최적화 전략, 수치적 기울기 테크닉을 적용
- 해시 엔트리 개수: 효율성을 위해 NeuralAngelo의 $2^{22}$보다 적은 $2^{19}$개를 각 해상도마다 활용
- 표면 재구성은 총 50만 iteration이상의 최적화를 거치며, 매 10만 iteration마다 Gaussian Splatting 최적화를 3만 iteration씩 수행
- 추가로 Vis-MVSNet의 포인트 클라우드를 통합
- 외부 장면 성분에 NeRF를 사용하고 내부 형상에 NeuS를 사용하는 NeRF++와 유사한 듀얼 네트워크 아키텍처를 채택
- RTX4090 1개에서 16시간 동안 학습
1. Comparisons to Baselines
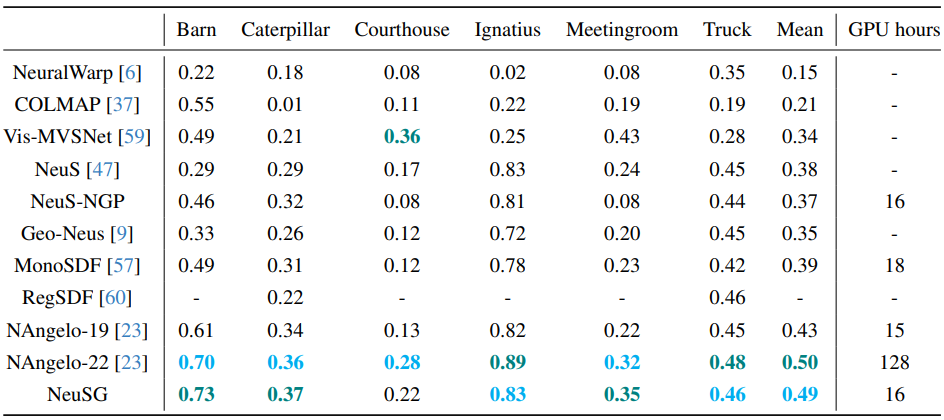
다음은 Tanks and Temples 데이터셋에서의 결과를 비교한 것이다. NAngelo-19와 NAngelo-22는 해시 엔트리 개수가 각각 $2^{19}$와 $2^{22}$인 NeuralAngelo이다.

2. Ablations
다음은 ablation study 결과이다.

다음은 scale 정규화와 normal 정규화에 대한 ablation 결과이다.