[논문리뷰] Neuralangelo: High-Fidelity Neural Surface Reconstruction

CVPR 2023. [Paper] [Page] [Github]
Zhaoshuo Li, Thomas Müller, Alex Evans, Russell H. Taylor, Mathias Unberath, Ming-Yu Liu, Chen-Hsuan Lin
NVIDIA Research | Johns Hopkins University
5 Jun 2023

Introduction

3D 표면 재구성은 서로 다른 시점에서 관찰된 여러 이미지로부터 dense한 기하학적 장면 구조를 복구하는 것을 목표로 한다. 복구된 표면은 증강/가상/혼합 현실을 위한 3D 에셋 생성이나 로봇의 자율 탐색을 위한 환경 매핑과 같은 많은 다운스트림 애플리케이션에 유용한 구조 정보를 제공한다. 단안 RGB 카메라를 사용한 3D 표면 재구성은 사용자에게 유비쿼터스 모바일 장치를 사용하여 현실 세계의 디지털 복사본을 자연스럽게 생성할 수 있는 기능을 제공하므로 특히 중요하다.

전통적으로 multi-view 스테레오 알고리즘은 sparse한 3D 재구성을 위해 선택되는 방법이었다. 그러나 이러한 알고리즘의 본질적인 단점은 균일한 색상의 넓은 영역, 반복적인 텍스처 패턴, 강한 색상 변화가 있는 영역 등 모호한 관찰을 처리할 수 없다는 것이다. 이로 인해 잡음이 있거나 표면이 누락되어 부정확하게 재구성될 수 있다. 최근 neural surface 재구성 방법은 이러한 한계를 해결하는 데 큰 잠재력을 보여주었다. 이 새로운 클래스의 방법은 좌표 기반 MLP를 사용하여 장면을 occupancy field 또는 signed distance function (SDF)과 같은 암시적 함수로 표현한다. MLP의 고유한 연속성과 neural volume rendering을 활용하는 이러한 기술을 통해 최적화된 표면이 공간 위치 간에 의미 있게 보간되어 부드럽고 완전한 표면 표현을 얻을 수 있다.

고전적인 접근법에 비해 neural surface 재구성 방법의 우월성에도 불구하고 현재 방법의 복구 충실도는 MLP의 용량에 맞게 확장되지 않는다. 최근 Instant NGP (Neural Graphics Primitives)라고 하는 새로운 확장 가능한 표현이 제안되었다. Instant NGP는 다중 해상도 해시 인코딩을 갖춘 하이브리드 3D 그리드 구조와 해상도에 로그 선형인 메모리 공간을 사용하여 더욱 표현력이 뛰어난 경량 MLP를 도입한다. 제안된 하이브리드 표현은 neural field의 표현 능력을 크게 향상시키고 객체 모양 표현과 새로운 view 합성 문제와 같은 다양한 task에 대해 매우 미세한 디테일을 표현하는 데 큰 성공을 거두었다.

본 논문에서는 충실도가 높은 표면 재구성을 위해 Neuralangelo를 제안하였다. Neuralangelo는 neural surface 렌더링을 통한 multi-view 이미지 관찰을 통해 최적화된 기본 3D 장면의 neural SDF 표현으로 Instant NGP를 채택하였다. 저자들은 다중 해상도 해시 인코딩의 잠재력을 완전히 활용하는 데 핵심적인 두 가지 결과를 제시하였다.

1. 수치적 기울기를 사용하여 eikonal regularization을 위한 표면 법선과 같은 고차 도함수를 계산하는 것이 최적화를 안정화하는 데 중요하다.
2. 점진적인 최적화 일정은 다양한 디테일 수준에서 구조를 복구하는 데 중요한 역할을 한다.

저자들은 이 두 가지 핵심 요소를 결합하고 표준 벤치마크와 실제 장면에 대한 광범위한 실험을 통해 재구성 정확도와 view 합성 품질 모두에서 이미지 기반 neural surface 재구성 방법에 비해 상당한 개선을 보여주었다.

Approach

Neuralangelo는 다중 시점 이미지에서 장면의 dense한 구조를 재구성한다. Neuralangelo는 카메라 view 방향을 따라 3D 위치를 샘플링하고 다중 해상도 해시 인코딩을 사용하여 위치를 인코딩한다. 인코딩된 feature는 SDF 기반 볼륨 렌더링을 사용하여 이미지를 합성하기 위해 SDF MLP와 컬러 MLP에 입력된다.

1. Preliminaries

Neural volume rendering

NeRF는 3D 장면을 볼륨 밀도 필드와 색상 필드로 나타낸다. 포즈를 취한 카메라와 광선 방향이 주어지면 볼륨 렌더링 방식은 광선을 따라 샘플링된 점의 color radiance를 통합한다. $i$번째 샘플링된 3D 위치 $x_i$는 카메라 중심으로부터 거리 $t_i$에 있다. 각 샘플링 지점의 부피 밀도 $\sigma_i$와 색상 $c_i$는 좌표 MLP를 사용하여 예측된다. 주어진 픽셀의 렌더링된 색상은 리만 합계로 근사화된다.

\[\begin{equation} \hat{c} (o, d) = \sum_{i=1}^N w_i c_i, \quad \textrm{where} \; w_i = T_i \alpha_i \end{equation}\]

여기서, $\alpha_i = 1 - \exp(-\sigma_i \delta_i)$는 $i$번째 광선 세그먼트의 불투명도이고, $\delta_i = t_{i+1} − t_i$는 인접한 샘플 사이의 거리이며, $T_i = \prod_{j=1}^{i−1} (1 − \alpha_j)$는 카메라에 도달하는 빛의 비율을 나타내는 누적 투과율이다. 네트워크를 supervise하기 위해 입력 이미지 $c$와 렌더링된 이미지 $\hat{c}$ 사이에 color loss가 사용된다.

\[\begin{equation} \mathcal{L}_\textrm{RGB} = \| \hat{c} - c \|_1 \end{equation}\]

그러나 이러한 밀도 공식을 사용하면 표면이 명확하게 정의되지 않는다. 밀도 기반 표현에서 표면을 추출하면 잡음이 많고 비현실적인 결과가 나오는 경우가 많다.

Volume rendering of SDF

가장 일반적인 표면 표현 중 하나는 SDF이다. SDF의 표면 $\mathcal{S}$는 암시적으로 zero-level set으로 표현될 수 있다.

\[\begin{equation} \mathcal{S} = \{x \in \mathbb{R}^3 \vert f(x) = 0\} \end{equation}\]

여기서 $f(x)$는 SDF 값이다. Neural SDF의 맥락에서 NeuS는 logistic function을 사용하여 NeRF의 볼륨 밀도 예측을 SDF 표현으로 변환하여 neural volume rendering으로 최적화할 것을 제안했다. 3D 점 $x_i$와 SDF 값 $f(x_i)$가 주어지면 불투명도 값 $\alpha_i$는 다음과 같이 계산된다.

\[\begin{equation} \alpha_i = \max \bigg( \frac{\Phi_s (f(x_i)) - \Phi_s (f(x_{i+1}))}{\Phi_s (f(x_i))} , 0 \bigg) \end{equation}\]

여기서 $\Phi_s$는 sigmoid 함수이. 본 논문에서는 동일한 SDF 기반 볼륨 렌더링 공식을 사용한다.

Multi-resolution hash encoding

최근 Instant NGP가 제안한 다중 해상도 해시 인코딩은 neural 장면 표현에 대한 뛰어난 확장성을 보여 주며 새로운 view 합성과 같은 task에 대한 세밀한 디테일을 생성한다. Neuralangelo에서는 고품질 표면을 복구하기 위해 해시 인코딩의 표현 능력을 채택한다.

해시 인코딩은 각 그리드 셀 모서리가 해시 엔트리에 매핑된 다중 해상도 그리드를 사용한다. 각 해시 엔트리는 인코딩 feature를 저장한다. \(\{V_1, \ldots, V_L\}\)을 서로 다른 그리드 해상도의 집합이라 하자. 입력 위치 $x_i$가 주어지면 이를 $x_{i,l} = x_i \cdot V_l$과 같이 각 그리드 해상도 $V_l$의 해당 위치에 매핑한다. 주어진 해상도 $V_l$에 대하여 feature 벡터 $\gamma_l (x_{i,l}) \in \mathbb{R}^c$는 그리드 셀 모서리에서 해시 엔트리의 trilinear interpolation을 통해 얻어진다. 모든 공간 해상도의 인코딩 feature는 함께 concat되어 $\gamma (x_i) \in \mathbb{R}^{cL}$개의 feature 벡터를 형성한다.

\[\begin{equation} \gamma (x_i) = (\gamma_1 (x_{i,1}), \ldots, \gamma_L (x_{i,L})) \end{equation}\]

그런 다음 인코딩된 feature는 얕은 MLP로 전달된다.

해시 인코딩의 한 가지 대안은 각 그리드 모서리가 충돌 없이 고유하게 정의되는 sparse voxel 구조이다. 그러나 volumetric feature 그리드에는 파라미터 수를 다루기 쉽게 만들기 위해 계층적 공간 분해 (ex. octrees)가 필요하다. 그렇지 않으면 공간 해상도에 따라 메모리가 3차적으로 증가한다. 이러한 계층 구조를 고려할 때 설계상 더 fine한 복셀 해상도는 더 coarse한 해상도로 잘못 표현된 표면을 복구할 수 없다. 대신 해시 인코딩은 공간 계층 구조가 없다고 가정하고 기울기 평균을 기반으로 자동으로 충돌을 해결한다.

2. Numerical Gradient Computation

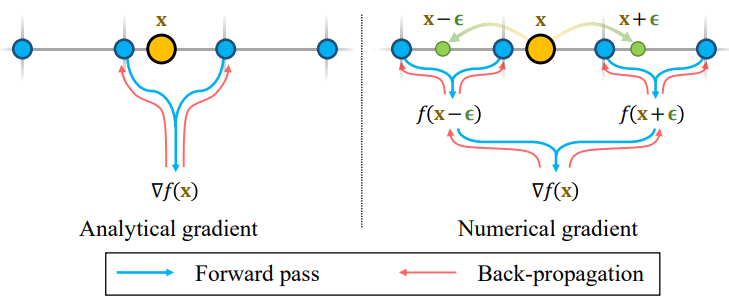
해시 인코딩 위치에 대한 해석적 기울기 (analytical gradient)는 locality로 인해 어려움을 겪는다. 따라서 최적화 업데이트는 로컬 해시 그리드에만 전파되며 로컬이 아닌 부드러움이 부족하다. 저자들은 수치적 기울기 (numerical gradient)를 사용하여 이러한 locality 문제에 대한 간단한 수정을 제안하였다. 개요는 위 그림에 나와 있다.

SDF의 특별한 속성은 단위 norm의 기울기에 따른 미분 가능성이다. SDF의 기울기는 거의 모든 곳에서 eikonal equation $| \nabla f(x) |_2 = 1$을 충족한다. 최적화된 neural 표현이 유효한 SDF가 되도록 강제하기 위해 일반적으로 SDF 예측에 eikonal loss가 적용된다.

\[\begin{equation} \mathcal{L}_\textrm{eik} = \frac{1}{N} \sum_{i=1}^N (\| \nabla f(x_i) \|_2 - 1)^2 \end{equation}\]

여기서 $N$은 샘플링된 포인트의 총 개수이다. End-to-end 최적화를 허용하려면 SDF 예측 $f(x)$에 대한 이중 역방향 연산이 필요하다.

SDF의 표면 법선 $\nabla f(x)$를 계산하는 사실상의 방법은 해석적 기울기 (analytical gradient)를 사용하는 것이다. 그러나 위치에 대한 해시 인코딩의 해석적 기울기는 trilinear interpolation 하에서 공간 전체에 걸쳐 연속적이지 않다. 복셀 그리드에서 샘플링 위치를 찾기 위해 각 3D 포인트 $x_i$는 먼저 그리드 해상도 $V_l$에 의해 크기 조정되고 $x_{i,l} = x_i \cdot V_l$로 작성된다. Trilinear interpolation에 대한 계수를 $\beta = x_{i,l} − \lfloor x_{i,l} \rfloor$로 둔다. 결과 feature 벡터는 다음과 같다.

\[\begin{equation} \gamma_l (x_{i,l}) = \gamma_l (\lfloor x_{i,l} \rfloor) \cdot (1 - \beta) + \gamma_l (\lceil x_{i,l} \rceil) \cdot \beta \end{equation}\]

여기서 반올림된 위치 $\lfloor x_{i,l} \rfloor$, $\lceil x_{i,l} \rceil$는 로컬 그리드 셀 모서리에 해당한다. 반올림 연산 $\lfloor \cdot \rfloor$와 $\lceil \cdot \rceil$는 미분할 수 없다. 결과적으로 위치에 대한 해시 인코딩의 미분은 다음과 같이 얻을 수 있다.

\[\begin{aligned} \frac{\partial \gamma_l (x_{i,l})}{\partial x_i} &= \gamma_l (\lfloor x_{i,l} \rfloor) \cdot (- \frac{\partial \beta}{\partial x_i}) + \gamma_l (\lceil x_{i,l} \rceil) \cdot \frac{\partial \beta}{\partial x_i} \\ &= \gamma_l (\lfloor x_{i,l} \rfloor) \cdot (- V_l) + \gamma_l (\lceil x_{i,l} \rceil) \cdot V_l \end{aligned}\]

해시 인코딩의 파생물은 로컬이다. 즉, $x_i$가 그리드 셀 경계를 넘어 이동할 때 해당 해시 엔트리가 달라진다. 따라서 \(\mathcal{L}_\textrm{eik}\)는 로컬로 샘플링된 해시 엔트리, 즉 $\gamma_l (\lfloor x_{i,l} \rfloor)$과 $\gamma_l (\lceil x_{i,l} \rceil)$에만 역전파된다. 연속 표면이 여러 그리드 셀에 걸쳐 있는 경우 이러한 그리드 셀은 갑작스러운 전환 없이 일관된 표면 법선을 생성해야 한다. 표면 표현의 일관성을 보장하려면 이러한 그리드 셀의 공동 최적화가 바람직하다. 그러나 모든 해당 그리드 셀이 동시에 샘플링되고 최적화되지 않는 한 해석적 기울기는 로컬 그리드 셀로 제한된다. 이러한 샘플링이 항상 보장되는 것은 아니다.

본 논문은 해시 인코딩의 해석적 기울기의 locality를 극복하기 위해 수치적 기울기를 사용하여 표면 법선을 계산하는 것을 제안한다. 수치적 기울기의 step 크기가 해시 인코딩의 그리드 크기보다 작은 경우 수치적 기울기는 해석적 기울기와 동일하다. 그렇지 않으면 여러 그리드 셀의 해시 엔트리가 표면 법선 계산에 참여하게 된다. 따라서 표면 법선을 통한 역전파를 통해 여러 그리드의 해시 엔트리가 동시에 최적화 업데이트를 받을 수 있다. 직관적으로 신중하게 선택한 step 크기의 수치적 기울기는 해석적 기울기 표현에 대한 smoothing 연산으로 해석될 수 있다. 법선 supervision의 대안은 teacher-student 커리큘럼으로, 예측된 noisy한 법선이 MLP 출력을 향해 구동되어 MLP들의 부드러움을 활용한다. 그러나 이러한 teacher-student loss로 인한 해석적 기울기는 여전히 해시 인코딩을 위해 로컬 그리드 셀로만 역전파된다. 대조적으로, 수치적 기울기는 추가 네트워크 없이도 locality 문제를 해결한다.

수치적 기울기를 사용하여 표면 법선을 계산하려면 추가 SDF 샘플이 필요하다. 샘플링된 포인트 $x_i$가 주어지면 step 크기 $\epsilon$ 부근 내에서 $x_i$ 주변의 표준 좌표의 각 축을 따라 두 개의 포인트를 추가로 샘플링한다. 예를 들어, 표면 법선의 $x$ 성분은 다음과 같이 구할 수 있다.

\[\begin{equation} \nabla_x f(x_i) = \frac{f(\gamma(x_i + \epsilon_x)) - f(\gamma(x_i - \epsilon_x))}{2 \epsilon}, \quad \epsilon_x = [\epsilon, 0, 0] \end{equation}\]

수치적 표면 법선 계산에는 총 6개의 추가 SDF 샘플이 필요하다.

3. Progressive Levels of Details

Coarse-to-fine 최적화는 잘못된 로컬 최소값에 빠지는 것을 방지하기 위해 loss 환경을 더 잘 형성할 수 있다. Neuralangelo는 점진적인 디테일 수준으로 표면을 재구성하기 위해 coarse-to-fine 최적화 방식을 채택하였다. 고차 도함수에 대한 수치적 기울기를 사용하면 자연스럽게 Neuralangelo가 두 가지 관점에서 coarse-to-fine 최적화를 수행할 수 있다.

Step size $\epsilon$

수치적 기울기는 step 크기 $\epsilon$가 해상도와 복구된 디테일의 양을 제어하는 smoothing 연산으로 해석될 수 있다. 수치적 표면 법선 계산을 위해 더 큰 $\epsilon$를 사용하여 \(\mathcal{L}_\textrm{eik}\)을 적용하면 표면 법선이 더 큰 규모에서 일관되게 유지되므로 일관되고 연속적인 표면이 생성된다. 반면, 더 작은 \(\epsilon$로 $\mathcal{L}_\textrm{eik}\)을 적용하면 더 작은 영역에 영향을 미치고 디테일을 매끄럽게 만드는 것을 방지한다. 실제로 step 크기 $\epsilon$을 가장 coarse한 해시 그리드 크기로 초기화하고 최적화 프로세스 전반에 걸쳐 다양한 해시 그리드 크기와 일치하도록 기하급수적으로 줄인다.

Hash grid resolution $V$

모든 해시 그리드가 최적화 시작부터 활성화되면 기하학적 디테일을 캡처하기 위해 fine한 해시 그리드는 먼저 큰 step 크기 $\epsilon$을 사용하여 coarse한 최적화에서 “unlearn”하고 더 작은 $\epsilon$을 사용하여 “relearn”해야 한다. 수렴 최적화로 인해 이러한 프로세스가 실패하면 기하학적 디테일이 손실된다. 따라서 초기의 coarse한 해시 그리드들만 활성화하고 $\epsilon$이 해당 공간 크기로 감소할 때 더 fine한 해시 그리드를 점진적으로 활성화한다. 따라서 디테일을 더 잘 포착하기 위해 재학습 과정을 피할 수 있다. 실제로 최종 결과를 지배하는 단일 해상도 feature를 피하기 위해 모든 파라미터에 대해 weight decay를 적용한다.

4. Optimization

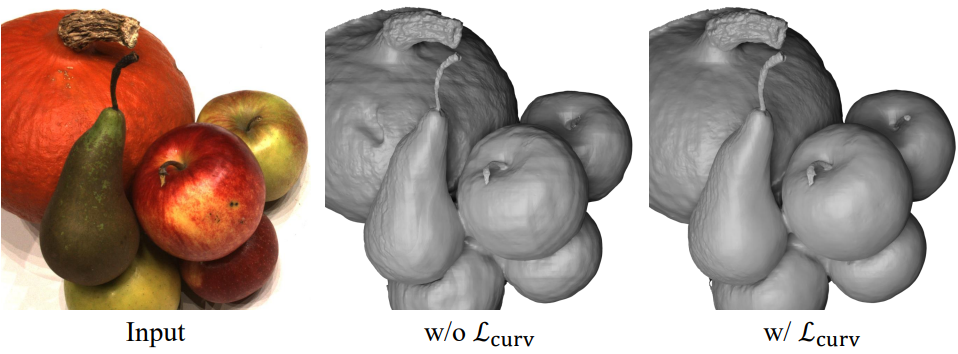
재구성된 표면의 매끄러움을 더욱 장려하기 위해 SDF의 평균 곡률을 정규화하여 prior를 적용한다. 평균 곡률은 표면 정규 계산과 유사한 discrete Laplacian에서 계산된다. 그렇지 않으면 trilinear interpolation을 사용할 때 해시 인코딩의 2차 해석적 기울기는 모든 곳에서 0이다. 곡률 loss \(\mathcal{L}_\textrm{curv}\)는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L}_\textrm{curv} = \frac{1}{N} \sum_{i=1}^N \vert \nabla^2 f(x_i) \vert \end{equation}\]

표면 법선 계산에 사용된 샘플을 곡률 계산에 사용할 수 있다. 총 loss는 loss의 가중 합으로 정의된다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{RGB} + w_\textrm{eik} \mathcal{L}_\textrm{eik} + w_\textrm{curv} \mathcal{L}_\textrm{curv} \end{equation}\]

MLP와 해시 인코딩을 포함한 모든 네트워크 파라미터는 공동으로 end-to-end로 학습된다.

Experiments

• 데이터셋: DTU, Tanks and Temples
• 구현 디테일
  • 해시 인코딩 해상도: $2^5$에서 $2^{11}$까지 16개의 레벨에 걸쳐 있음
  • 각 해시 엔트리의 채널 크기: 8
  • 각 해상도의 최대 해시 엔트리 수: $2^{22}$
  • 최적화 시작 시 활성화하는 해시 해상도 수: DTU는 4, Tanks and Temples는 8
  • 5000 iteration마다 새로운 해시 해상도를 활성화

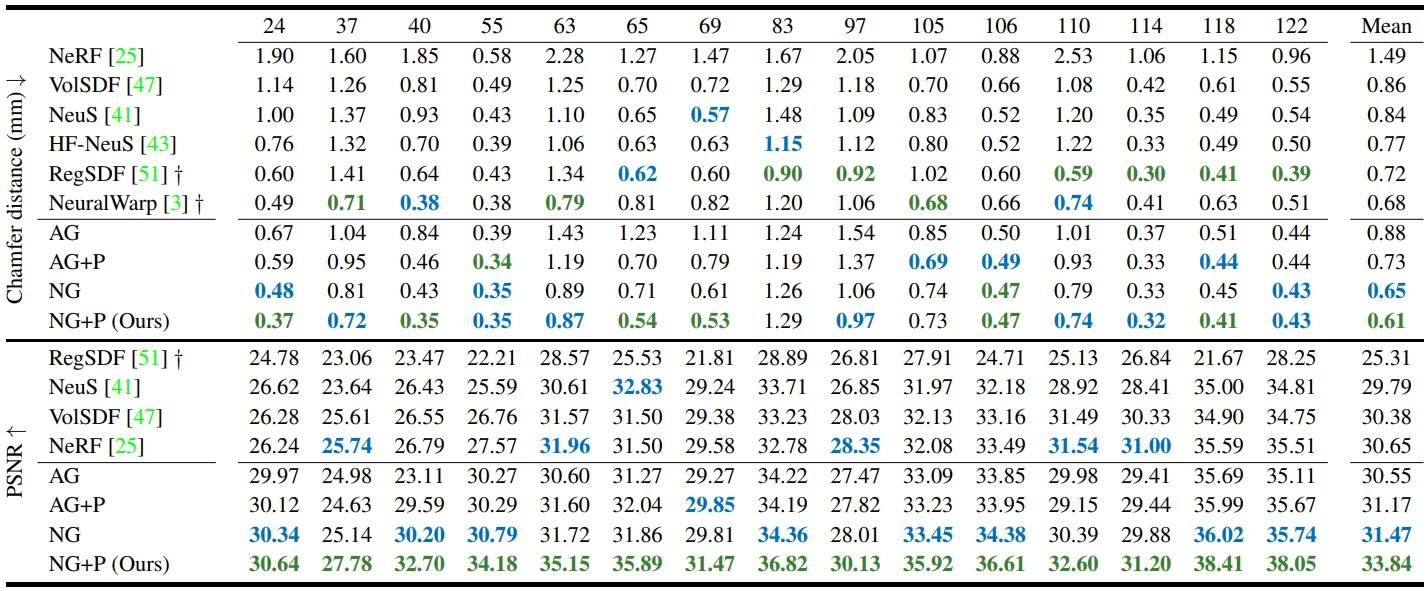
1. DTU Benchmark

다음은 DTU 벤치마크에서의 정성적 비교 결과이다.

다음은 DTU 벤치마크에서의 정량적 비교 결과이다.

다음은 여러 coarse-to-fine 방식에 대한 정석적 비교 결과이다.

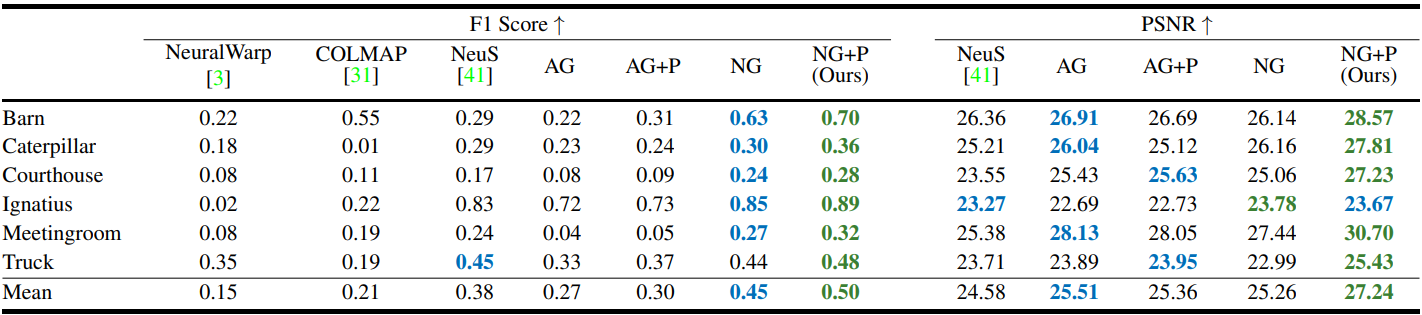
2. Tanks and Temples

다음은 Tanks and Temples 데이터셋에 대한 정성적 비교 결과이다.

다음은 Tanks and Temples 데이터셋에 대한 정량적 비교 결과이다.

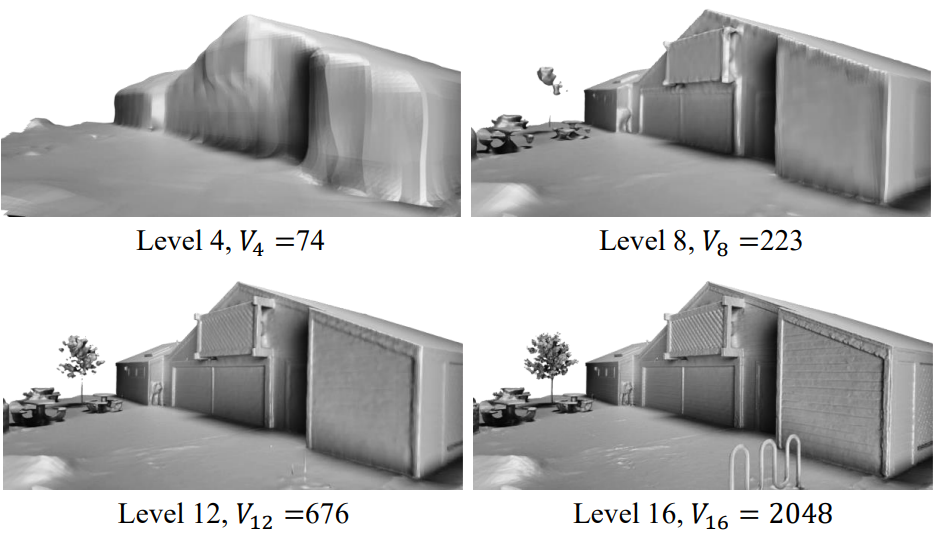
3. Level of Details

다음은 여러 해시 해상도에서의 결과이다.

4. Ablations

다음은 곡률 정규화에 대한 ablation 결과이다.

다음은 topology warmup에 대한 ablation 결과이다.