[논문리뷰] Neural Ordinary Differential Equations (Neural ODE)
NeurIPS 2018. [Paper] [Github]
Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, David Duvenaud
University of Toronto, Vector Institute
19 Jun 2018
Introduction
ResNet, RNN 디코더, normalizing flow와 같은 모델들은 변환들의 시퀀스를 hidden state로 구성하여 복잡한 변환을 구축한다.
\[\begin{equation} h_{t+1} = h_t + f(h_t, \theta_t), \quad \textrm{where} \; t \in \{0, \ldots, T\}, \; h_t \in \mathbb{R}^D \end{equation}\]이 반복적이 업데이트는 연속적인 변환의 Euler discretization으로 볼 수 있다.
더 많은 레이어를 추가하고 더 작은 step을 수행하면 어떻게 될까? 극한으로 가면 다음과 같이 신경망에 대한 상미분 방정식(ODE)을 사용하여 hidden unit의 연속적인 역학을 parameterize한다.
\[\begin{equation} \frac{dh(t)}{dt} = f(h(t), t, \theta) \end{equation}\]입력 레이어 $h(0)$에서 시작하여 출력 레이어 $h(T)$를 특정 시간 $T$에서 이 ODE 초기값 문제에 대한 해로 정의할 수 있다. 이 값은 블랙박스 ODE solver로 계산할 수 있다. 원하는 정확도로 해를 결정하는 데 필요할 때마다 hidden unit의 역학 $f$를 평가한다. 아래 그림은 이러한 두 가지 접근 방식을 대조한 것이다.

ODE solver를 사용하여 모델을 정의하고 평가하면 다음과 같은 이점이 있다.
- 메모리 효율성: 본 논문은 solver의 연산을 통해 역전파하지 않고 ODE solver의 모든 입력에 대해 스칼라 값 loss의 기울기를 계산하는 방법을 제시하였다. Forward pass의 중간 값들을 저장하지 않으면 모델 깊이에 대하여 일정한 메모리 비용으로 모델을 학습시킬 수 있다.
- 적응형 계산: Euler’s method는 아마도 ODE를 푸는 가장 간단한 방법일 것이다. 그 이후로 효율적이고 정확한 ODE solver가 개발된 지 120년이 넘었다. 최신 ODE solver는 근사 오차의 증가를 보장하고, 오차 수준을 모니터링하며, 평가 전략을 즉시 조정하여 요청된 정확도 수준을 달성한다. 이를 통해 문제의 복잡도에 따라 모델 평가 비용을 확장할 수 있다. 학습 후에는 실시간 또는 저전력 애플리케이션의 정확도가 낮아질 수 있다.
- Scalable하고 가역인 normalizing flow: 연속적인 변환의 예상치 못한 부수적 이점은 change of variables 수식을 계산하기가 더 쉬워진다는 것이다. 이를 통해 normalizing flow의 bottleneck을 피하고 maximum likelihood에 의해 직접 학습할 수 있는 새로운 클래스의 가역 밀도 모델을 구성할 수 있다.
- 연속적인 시계열 모델: 이산적인 관찰 및 방출 간격이 필요한 RNN과 달리 연속적으로 정의된 역학은 임의의 시간에 도착하는 데이터를 자연스럽게 통합할 수 있다.
Reverse-mode automatic differentiation of ODE solutions
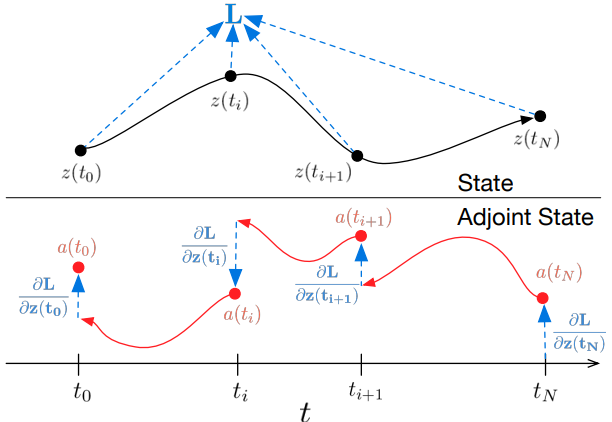
연속적인 깊이의 신경망을 학습할 때 가장 큰 기술적 어려움은 ODE solver를 통해 역방향 미분(역전파)을 수행하는 것이다. Forward pass의 연산을 통한 미분은 간단하지만 메모리 비용이 많이 들고 추가적인 수치적 오차가 발생한다.
ODE solver를 블랙박스로 취급하고 adjoint sensitivity method를 사용하여 기울기를 계산한다. 이 접근 방식은 새로운 두 번째 ODE를 시간에 대하여 거꾸로 풀어서 기울기를 계산하며 모든 ODE solver에 적용 가능하다. 이 접근 방식은 문제 크기에 따라 선형적으로 확장되고 메모리 비용이 낮으며 수치적 오차를 명시적으로 제어한다.
입력이 ODE solver의 결과인 스칼라 값 loss function $L$을 최적화하는 것을 고려해보자.
\[\begin{equation} L(z(t_1)) = L \bigg( z(t_0) + \int_{t_0}^{t_1} f(z(t), t, \theta \bigg) dt) = L (\textrm{ODESolve} (z(t_0), f, t_0, t_1, \theta)) \end{equation}\]$L$을 최적화하려면 $\theta$에 대한 기울기가 필요하다. 첫 번째 단계는 loss의 기울기가 각 순간의 hidden state $z(t)$에 어떻게 의존하는지 결정하는 것이다. 이 quantity를 adjoint $a(t) = \partial L / \partial z(t)$라고 한다. Adjoint의 역학은 또 다른 ODE에 의해 제공되며, 이는 chain rule의 순간적 유사체로 생각할 수 있다.
\[\begin{equation} \frac{d a(t)}{dt} = - a(t)^\top \frac{\partial f (z(t), t, \theta)}{\partial z} \end{equation}\]ODE solver에 대한 또 다른 call을 통해 $\partial L / \partial z(t_0)$를 계산할 수 있다. 이 solver는 $\partial L / \partial z(t_1)$의 초기 값부터 시작하여 거꾸로 실행되어야 한다. 한 가지 복잡한 점은 이 ODE를 풀려면 전체 궤적을 따라 $z(t)$의 값을 알아야 한다는 것이다. 그러나 최종 값 $z(t_1)$부터 시작하여 $z(t)$를 adjoint와 함께 시간에 대해 거꾸로 다시 계산할 수 있다.
파라미터 $\theta$에 대한 기울기를 계산하려면 $z(t)$와 $a(t)$에 따라 달라지는 세 번째 적분을 계산해야 한다.
\[\begin{equation} \frac{d L}{d \theta} = - \int_{t_1}^{t_0} a(t)^\top \frac{\partial f (z(t), t, \theta)}{\partial \theta} dt \end{equation}\](4)와 (5)의 vector-Jacobian product $a(t)^\top \frac{\partial f}{\partial z}$와 $a(t)^\top \frac{\partial f}{\partial \theta}$는 $f$를 평가하는 것과 유사한 시간 비용으로 자동 미분을 통해 효율적으로 평가할 수 있다. z, a를 풀기 위한 모든 적분
$z$, $a$, $\frac{\partial L}{\partial \theta}$를 풀기 위한 모든 적분은 원래 state, adjoint, 기타 편도함수를 하나의 벡터로 concatenate하고 ODE solver에 대한 하나의 call로 계산될 수 있다. Algorithm 1은 필요한 역학을 구성하고 ODE solver를 call하여 모든 기울기를 한 번에 계산하는 방법을 보여준다.

대부분의 ODE solver에는 state $z(t)$를 여러 번 출력하는 옵션이 있다. Loss가 이러한 중간 state에 따라 달라지는 경우 역방향 미분은 각각의 연속적인 출력 시간 쌍 사이에 하나씩 별도의 해석 시퀀스로 나누어야 한다. 각 관찰에서 adjoint는 해당 편도함수 $\partial L / \partial z(t_i)$의 방향으로 조정되어야 한다.
Replacing residual networks with ODEs for supervised learning
- ODE solver: Adams method (LSODE와 VODE에 구현되어 있음)
- 모델 아키텍처: 입력을 두 번 다운샘플링한 다음 6개의 표준 residual block을 적용하는 작은 ResNet (ODE-Net)
다음은 MNSIT에서의 성능을 비교한 표이다.

RK-Net은 동일한 아키텍처를 사용하지만 Runge-Kutta 적분기를 통해 기울기가 직접 역전파되는 네트워크이다. $L$은 ResNet의 레이어 수이고, $\tilde{L}$은 ODE solver가 한 번의 forward pass에서 요청한 함수 평가 횟수이다. ODE-Net과 RK-Net 모두 ResNet과 비슷한 성능을 달성하였다.
Error Control in ODE-Nets
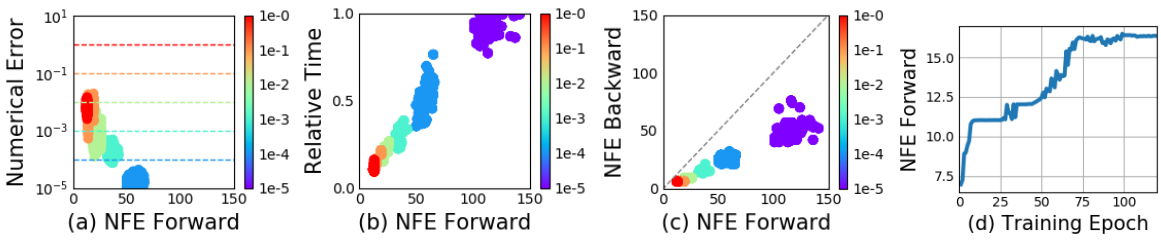
ODE solver는 출력이 실제 해의 주어진 허용오차 내에 있는지 대략적으로 확인할 수 있다. 이 허용오차를 변경하면 네트워크의 동작이 변경된다. 먼저 위 그림의 (a)를 보면 오차가 실제로 제어될 수 있음을 확인할 수 있다. Forward call에 소요되는 시간은 함수 평가 횟수(NFE)에 비례하므로 (위 그림의 (b)), 허용오차를 조정하면 정확도와 계산 비용 사이의 trade-off를 얻을 수 있다. 높은 정확도로 학습할 수 있지만 테스트 시 더 낮은 정확도로 전환할 수 있다.
위 그림의 (c)는 놀라운 결과를 보여준다. Backward pass의 평가 횟수는 forward pass의 대략 절반이다. 이는 adjoint sensitivity method가 적분기를 통해 직접 역전파하는 것보다 메모리 효율적일 뿐만 아니라 계산상 효율적이라는 것을 의미한다. 왜냐하면 직접 역전파 하는 접근 방식은 forward pass에서 각 함수 평가를 통해 역전파해야 하기 때문이다.
Network Depth
ODE 해의 ‘깊이’를 정의하는 방법은 명확하지 않다. 관련된 quantity는 필요한 hidden state 동역학의 평가 횟수이며, 세부 사항은 ODE solver에 위임되고 초기 state 또는 입력에 따라 달라진다. 위 그림의 (d)는 학습 전반에 걸쳐 함수 평가 횟수가 증가한다는 것을 보여 주며, 아마도 모델의 복잡도 증가에 적응할 것이다.
Continuous Normalizing Flows
이산화된 방정식 $\frac{dh(t)}{dt} = f(h(t), t, \theta)$는 normalizing flow와 NICE에서도 등장한다. 이 방법들은 샘플이 전단사 함수 $f$를 통해 변환되는 경우 change of variables 정리를 사용하여 확률의 정확한 변화를 계산한다.
\[\begin{equation} z_1 = f(z_0) \; \implies \; \log p(z_1) = \log p(z_0) - \log \bigg\vert \textrm{det} \frac{\partial f}{\partial z_0} \bigg\vert \end{equation}\]일반적으로 change of variables 공식의 주요 한계점은 $z$의 차원 또는 hidden unit 수에서 세제곱에 비례하는 비용을 갖는 Jacobian $\partial f / \partial z$의 determinant(행렬식)을 계산하는 것이다. 최근 연구들에서는 normalizing flow layer의 표현력과 계산 비용 간의 trade-off를 연구하였다.
놀랍게도 이산적인 레이어의 집합에서 연속적인 변환으로 이동하면 normalizing 상수의 변화 계산이 단순화된다.
$z(t)$를 시간에 따른 확률 $p(z(t))$를 갖는 유한하고 연속적인 확률 변수라고 하자. 그리고 $\frac{dz}{dt} = f(z(t), t)$를 $z(t)$의 시간에 대해 연속적인 변환을 설명하는 미분 방정식이라고 하자. $f$가 $z$에서 균일하게 Lipschitz 연속이고 $t$에서 연속이라고 가정하면 로그 확률의 변화는 다음과 같은 미분 방정식을 따른다.
\[\begin{equation} \frac{\partial \log p(z(t))}{\partial t} = -\textrm{tr} \bigg( \frac{df}{dz(t)} \bigg) \end{equation}\]Jacobian의 determinant를 계산하는 대신 trace(대각합) 연산만 하면된다. 또한 일반적인 유한한 flow와 달리 미분 방정식 $f$는 전단사일 필요가 없다. 왜냐하면 고유성이 만족되면 전체 변환이 자동으로 전단사이기 때문이다.
초기 분포 $p(z(0))$가 주어지면 $p(z(t))$에서 샘플링하고 이 결합된 ODE를 풀어 밀도를 평가할 수 있다.
Using multiple hidden units with linear cost
Determinant는 선형 함수가 아니지만 trace 함수는 선형 함수이다. 이는 $\textrm{tr}(\sum_n J_n) = \sum_n \textrm{tr}(J_n)$을 의미한다. 따라서 역학이 함수의 합으로 주어지면 로그 밀도에 대한 미분 방정식도 합이 된다.
\[\begin{equation} \frac{dz(t)}{dt} = \sum_{n=1}^M f_n (z(t)) \; \implies \; \frac{d \log p(z(t))}{dt} = \sum_{n=1}^M \textrm{tr} \bigg( \frac{df_n}{dz(t)} \bigg) \end{equation}\]이는 hidden unit이 많은 flow model을 낮은 비용으로 평가할 수 있음을 의미하며 비용은 hidden unit 수 $M$에 선형이다. 표준 normalizing flow를 사용하여 이러한 ‘넓은’ flow layer를 평가하는 데는 $\mathcal{O}(M^3)$의 비용이 든다. 이는 표준 normalizing flow 아키텍처가 하나의 hidden unit의 여러 레이어를 사용한다는 것을 의미한다.
Time-dependent dynamics
저자들은 flow의 파라미터를 $t$의 함수로 지정하여 미분 방정식 $f(z(t), t)$를 $t$에 따라 변경할 수 있도록 하였다. 이는 일종의 hypernetwork이다. 또한 각 hidden unit에 대한 gating 메커니즘인 $\frac{dz}{dt} = \sum_n \sigma_n (t) f_n(z)$를 도입하였다. 여기서 $\sigma_n (t) \in (0, 1)$은 역학 $f_n (z)$가 언제 적용되어야 하는지 학습하는 신경망이다. 이러한 모델을 continuous normalizing flow (CNF)라고 부른다.
1. Experiments with Continuous Normalizing Flows
Density matching
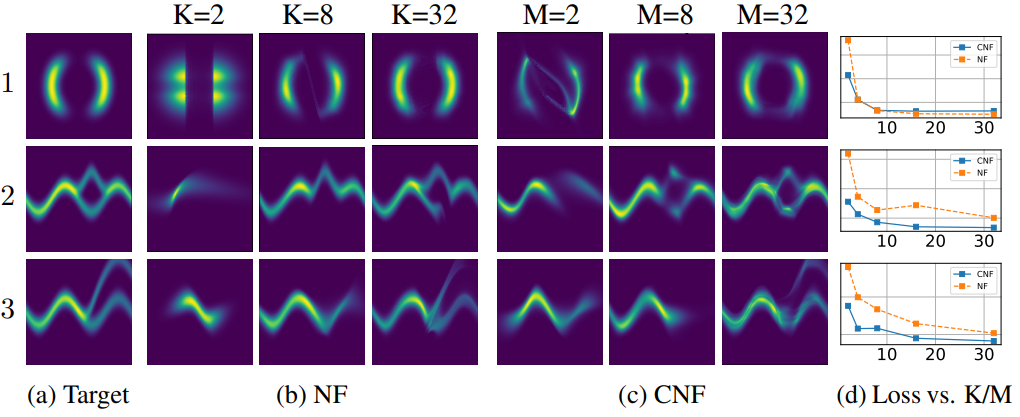
저자들은 위에서 설명한 대로 CNF를 구성하고 Adam을 사용하여 1만 번의 iteration으로 학습시켰다. 대조적으로, NF는 RMSprop을 사용하여 50만 번의 iteration으로 학습되었다. Flow model을 $q$라고 하면, 타겟 밀도 $p(\cdot)$가 평가될 수 있는 loss function인 \(\textrm{KL}(q(x)\|p(x))\)을 최소화한다. 위 그림은 CNF가 일반적으로 더 낮은 loss를 달성한다는 것을 보여준다.
Maximum Likelihood Training
CNF의 유용한 속성은 forward pass와 거의 동일한 비용으로 역변환을 계산할 수 있다는 것이다. 이는 NF는 불가능하다. 이를 통해 maximum likelihood estimation (MLE)을 수행하여 밀도 추정 task에 대한 flow model을 학습시킬 수 있다. 이는 적절히 change of variables 정리를 사용하여 $q(\cdot)$를 계산하고 $\mathbb{E}_p(x) [q(x)]$를 최대화한 다음 CNF를 역전시켜 $q(x)$에서 랜덤 샘플을 생성한다.
저자들은 64개의 hidden unit으로 CNF를 구성하였고, hidden unit이 1개인 레이어 64개를 쌓아 NF를 구성하였다.
다음은 noise에서 데이터로 변환하는 과정을 시각화한 것이다.
A generative latent function time-series model
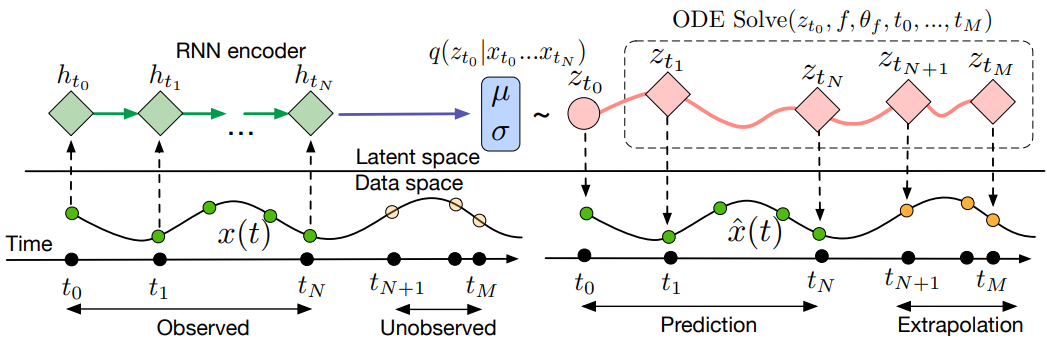
불규칙하게 샘플링된 데이터에 신경망을 적용하는 것은 어렵다. 일반적으로 관측값은 고정된 기간의 저장소에 저장되고 latent의 역학은 동일한 방식으로 이산화된다. 이로 인해 누락된 데이터와 잘못 정의된 latent 변수로 인해 어려움이 발생한다. 누락된 데이터는 생성적 시계열 모델 또는 데이터 대치를 사용하여 해결할 수 있다. 또 다른 접근 방식은 타임스탬프 정보를 RNN의 입력에 concatenate하는 것이다.
저자들은 시계열 모델링에 대한 연속적이고 생성적인 접근 방식을 제시하였다. 본 논문의 모델은 latent 궤적을 통해 각 시계열을 나타낸다. 각 궤적은 로컬한 초기 상태 $z_{t_0}$와 모든 시계열에서 공유되는 글로벌한 latent 역학 집합에서 결정된다. 관찰 시간 $t_0, t_1, \ldots, t_N$과 초기 상태 $z_{t_0}$가 주어지면 ODE solver는 $z_{t_1}, \ldots z_{t_N}$을 생성하며, 이는 각 관찰에서 latent 상태를 설명한다. 저자들은 다음과 같은 샘플링 절차를 통해 이 생성 모델을 정의하였다.
\[\begin{aligned} z_{t_0} &\sim p (z_{t_0}) \\ z_{t_1}, \ldots, z_{t_N} &= \textrm{ODESolve} (z_{t_0}, f, \theta, t_0, \ldots, t_N) \\ \textrm{each} \quad x_{t_i} &\sim p(x \vert z_{t_i}, \theta_x) \end{aligned}\]함수 $f$는 현재 timestep에서 $z$를 취하고 기울기 $\frac{\partial z(t)}{\partial t} = f(z(t), \theta_f)$를 출력하는 time-invariant(시불변) 함수이다. 저자들은 신경망을 사용하여 이 함수를 parameterize하였다. $f$는 time-invariant이므로 latent 상태 $z(t)$가 주어지면 전체 latent 궤적이 고유하게 정의된다. 이 latent 궤적을 추정하면 시간적으로 훨씬 앞이나 뒤로 임의로 예측할 수 있다.
Training and Prediction
시퀀스 값 관측을 사용하여 이 latent 변수 모델을 VAE로 학습시킬 수 있다. 인식 네트워크는 RNN으로, 시간을 거꾸로 거슬러 올라가 순차적으로 데이터를 소비하고 $q_\phi (z_0 \vert x_1, x_2, \ldots, x_N)$을 출력한다. ODE를 생성 모델로 사용하면 연속적인 타임라인에서 임의의 시점 $t_1, \ldots, t_M$에 대한 예측을 할 수 있다.
Poisson Process likelihoods
관찰이 발생했다는 사실은 종종 latent 상태에 대해 알려준다. 이벤트 비율은 latent 상태의 함수인 $p( \textrm{event at time } t \vert z(t)) = \lambda(z(t))$의 함수로 parameterize될 수 있다. 이 비율 함수가 주어지면 간격 내 일련의 독립적인 관측 시간의 likelihood는 다음과 같은 비균질 포아송 프로세스에 의해 제공된다.
\[\begin{equation} \log p(t_1, \ldots, t_N \; \vert \; t_\textrm{start}, t_\textrm{end}) = \sum_{i=1}^N \log \lambda(z(t_i)) - \int_{t_\textrm{start}}^{t_\textrm{end}} \lambda (z(t)) dt \end{equation}\]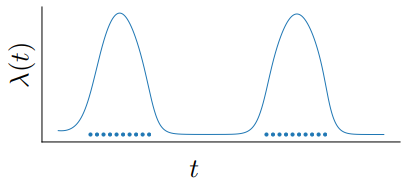
다른 신경망을 사용하여 $\lambda(\cdot)$를 parameterize할 수 있다. ODE solver에 대한 단일 call로 latent 궤적과 포아송 프로세스 likelihood를 편리하게 함께 평가할 수 있다. 위 그림은 토이 데이터셋에서 이러한 모델이 학습한 이벤트 비율을 보여준다.
관측 시간에 대한 포아송 프로세스 likelihood는 데이터 likelihood와 결합되어 모든 관측과 관측이 이루어진 시간을 공동으로 모델링할 수 있다.
1. Time-series Latent ODE Experiments
저자들은 latent ODE 모델이 시계열을 피팅하고 추정하는 능력을 조사하였다. 인식 네트워크는 25개의 hidden unit이 있는 RNN이며, 4차원의 latent space를 사용한다. 20개의 hidden unit이 있는 1개의 hidden layer 네트워크를 사용하여 역학 함수 $f$를 parameterize한다. $p(x_{t_i} \vert z_{t_i})$를 계산하는 디코더는 20개의 hidden unit이 있는 하나의 hidden layer가 있는 또 다른 신경망이다. Baseline은 negative Gaussian log-likelihood를 최소화하도록 학습된 25개의 hidden unit이 있는 RNN이다. 저자들은 불규칙한 관측으로 RNN을 돕기 위해 입력이 다음 관측과의 시간차와 concatenate되는 이 RNN의 두 번째 버전을 학습시켰다.
Bi-directional spiral dataset
저자들은 각각 다른 지점에서 시작하고 100개의 동일한 간격의 timestep으로 샘플링된 1000개의 2차원 나선 데이터셋을 생성했다. 데이터셋에는 두 가지 유형의 나선이 포함되어 있다. 절반은 시계 방향이고 나머지 절반은 시계 반대 방향이다. Task를 보다 현실적으로 만들기 위해 관측값에 Gaussian noise를 추가하였다.
Time series with irregular time points
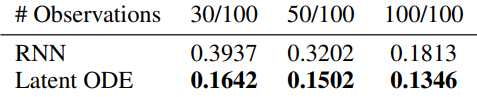
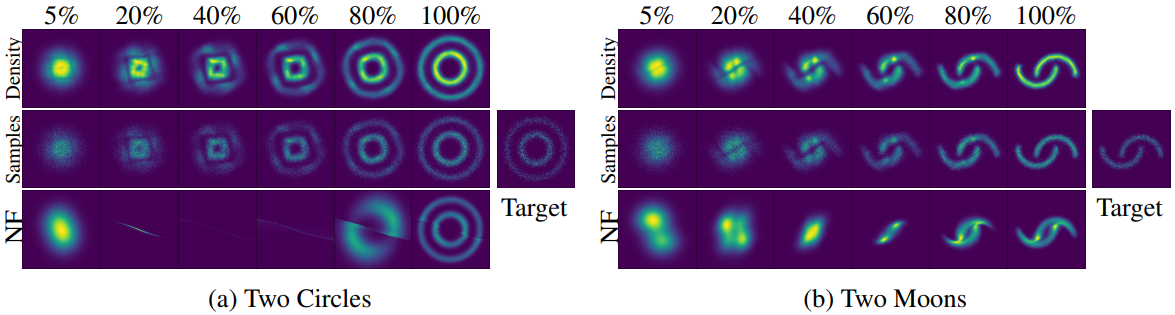
불규칙한 타임스탬프를 생성하기 위해 교체 없이 각 궤적에서 포인트를 무작위로 샘플링한다 (\(n = \{30, 50, 100\}\)). 저자들은 학습에 사용된 시점을 넘어서는 100개 시점에 대한 예측 RMSE(평균 제곱근 오차)를 측정하였다. 위 표는 latent ODE의 예측 RMSE가 상당히 낮다는 것을 보여준다.
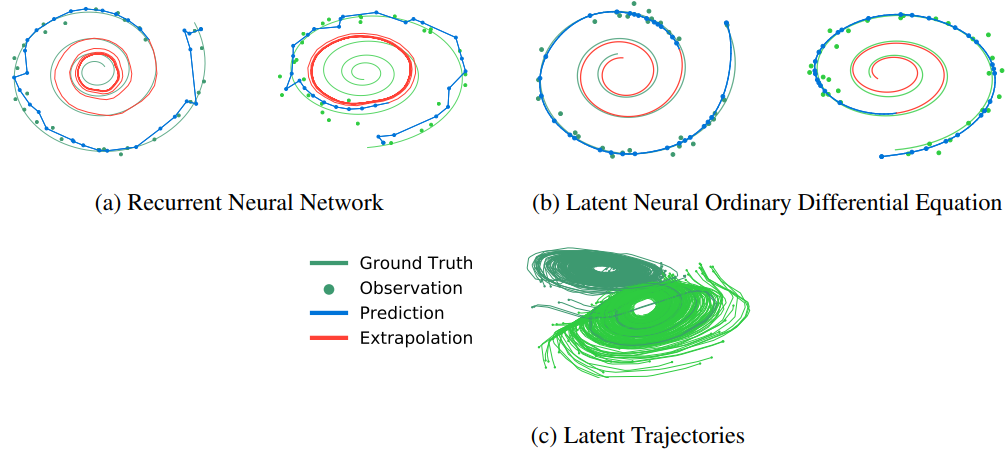
위 그림은 30개의 서브샘플링 포인트를 사용한 나선형 재구성의 예시이다. Latent ODE로부터의 재구성은 latent 궤적의 사후 확률(posterior)에서 샘플링하고 이를 데이터 공간으로 디코딩하여 얻었다. 관측된 지점 수와 noise에도 불구하고 재구성과 추정이 ground-truth와 일치한다는 것을 관찰할 수 있다.
Latent space interpolation
위 그림의 (c)는 latent space의 처음 두 차원에 project된 latent 궤적을 보여준다. 궤적은 두 개의 개별 궤적 클러스터를 형성한다. 하나는 시계 방향 나선으로 디코딩되고 다른 하나는 시계 반대 방향으로 디코딩된다.
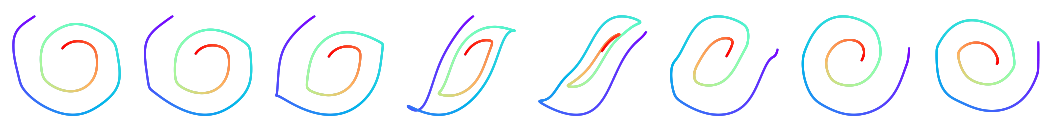
위 그림은 latent 궤적이 시계 방향에서 시계 반대 방향 나선형으로 전환하면서 초기 지점 $z(t_0)$의 함수로 부드럽게 변하는 것을 보여준다.
Limitations
- Minibatching: Mini-batch의 사용이 일반적인 신경망보다 덜 간단하다. 각 batch 요소의 상태를 함께 연결하여 차원 $D \times K$의 결합된 ODE를 생성함으로써 ODE solver를 통해 일괄적으로 평가를 수행할 수 있다. 경우에 따라 모든 batch 요소의 오차를 함께 제어하려면 결합된 시스템을 $K$배 더 평가해야 할 수도 있다. 각 시스템을 개별적으로 해결하는 경우보다 자주 발생한다. 그러나 실제로 mini-batch를 사용하면 평가 횟수가 크게 증가하지 않는다.
- 유일성: Picard의 존재성 정리는 미분 방정식이 $z$에서 균일하게 Lipschitz 연속이고 $t$에서 연속인 경우 초기 값 문제에 대한 해가 존재하고 유일하다는 것을 나타낸다. 이 정리는 신경망에 유한한 가중치가 있고 tanh 또는 relu와 같은 Lipshitz nonlinearity들을 사용하는 경우 모델에 적용된다.
- 오차 허용치 설정: 사용자가 속도와 정밀도를 절충할 수 있지만 학습 중에 forward 및 backward pass 모두에서 오차 허용치를 선택해야 한다.
- Forward 궤적 재구성: 역학을 거꾸로 실행하여 상태 궤적을 재구성하면 재구성된 궤적이 원본에서 벗어나는 경우 수치적 오차가 추가로 발생할 수 있다. 이 문제는 체크포인트를 통해 해결될 수 있다.