[논문리뷰] NeRF On-the-go: Exploiting Uncertainty for Distractor-free NeRFs in the Wild
CVPR 2024. [Paper] [Page] [Github]
Weining Ren, Zihan Zhu, Boyang Sun, Jiaqi Chen, Marc Pollefeys, Songyou Peng
ETH Zurich | Microsoft | MPI for Intelligent Systems
29 May 2024

Introduction
NeRF 모델을 학습시키려면 카메라 포즈가 주어진 RGB 이미지 세트가 필요하고 초점 거리, 노출, 화이트 밸런스와 같은 카메라 설정을 수동으로 조정해야 한다. 또한 NeRF는 움직이는 물체, 그림자 또는 기타 동적 요소와 같은 방해 요소 없이 캡처 프로세스 중에 장면이 완전히 정적이어야 한다.
하지만 현실 세계는 본질적으로 동적이므로 방해 요소 없는 이러한 요구 사항을 충족하는 것은 종종 비현실적이다. 또한 캡처된 데이터에서 방해 요소를 제거하는 것은 어려운 일이다. 각 이미지에 대한 픽셀별 주석이 필요하며, 특히 큰 장면을 오랫동안 캡처하는 경우 매우 노동 집약적인 절차이다. 이는 동적인 실제 환경에서 NeRF를 실제로 적용하는 데 있어 주요한 한계점이다.
NeRF-W는 볼륨 렌더링을 통해 무작위로 초기화된 임베딩에서 픽셀별 불확실성을 최적화하였다. 이러한 설계는 이미지의 사전 정보를 무시하고 불확실성을 radiance field 재구성과 얽히게 하는 문제점이 존재한다. D²NeRF은 동영상 입력을 위해 정적 장면과 동적 장면을 분해할 수 있지만 sparse한 이미지 입력에서는 성능이 저하된다. RobustNeRF는 방해 요소를 outlier로 모델링하고 간단한 시나리오에서 인상적인 결과를 보여주었다. 그럼에도 불구하고 복잡한 실제 장면에서는 성능이 크게 떨어진다.
방해 요소의 비율에 관계없이, 우연히 찍은 이미지로부터 실제 장면에 대한 NeRF를 구축할 수 있을까?
본 논문은 효과적인 방해물 제거를 위해 설계된 plug-and-play 모듈인 NeRF On-the-go를 소개하며, 이를 통해 우연히 촬영한 모든 이미지에서 NeRF를 빠르게 학습할 수 있다. NeRF On-the-go는 세 가지 핵심 측면에 기반을 두고 있다.
- DINOv2 feature를 활용하여 feature 추출에서 robustness와 시공간적 일관성을 확보하고, 이를 통해 작은 MLP가 샘플당 픽셀 불확실성을 예측한다.
- SSIM 기반 loss를 활용하여 불확실성 최적화를 개선하고, 전경 방해물과 정적 배경 간의 구분을 강화힌다.
- 분리된 학습 전략을 사용하여 NeRF의 이미지 재구성 loss에 추정된 불확실성을 통합하여 방해물 제거를 크게 개선한다.
NeRF On-the-go는 작은 물체가 있는 좁은 실내 장면에서부터 복잡하고 대규모의 거리 장면에 이르기까지 광범위한 시나리오에서 robustness를 보여주며, 다양한 수준의 방해물을 효과적으로 처리할 수 있다. 특히, On-the-go 모듈은 RobustNeRF와 비교했을 때 NeRF 학습을 최대 10배까지 상당히 가속화할 수 있다. 이러한 효율성은 최신 NeRF 프레임워크와의 간단한 통합과 결합되어 NeRF On-the-go를 역동적인 실제 환경에서 NeRF 학습을 향상시키는 데 접근 가능하고 강력한 도구로 만든다.
Method
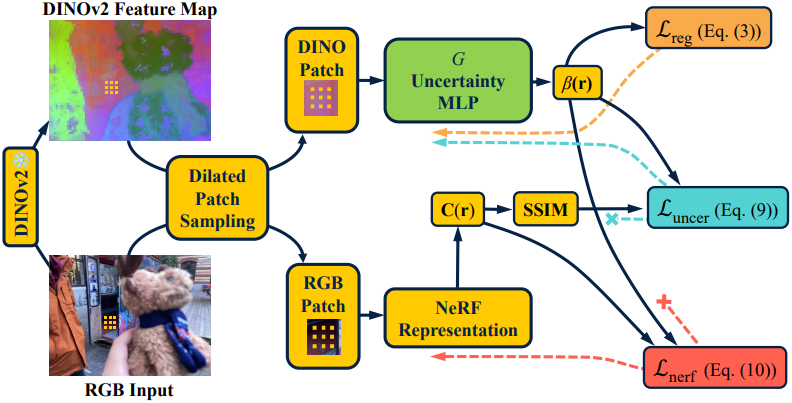
1. Uncertainty Prediction with DINOv2 Features
본 논문의 목표는 여러 이미지에 나타나는 방해 요소를 효과적으로 식별하고 제거하는 것이다. 이를 위해 뷰 전체에서 시공간적 일관성을 유지할 수 있는 것으로 나타난 DINOv2 feature를 활용한다.
이미지 feature 추출
RGB 이미지에 사전 학습된 DINOv2 feature 추출기 $\mathcal{E}$를 사용해 픽셀별 feature를 도출한다.
\[\begin{equation} \mathcal{F}_i = \mathcal{E} (\mathcal{I}_i), \quad \mathcal{E} \in \mathbb{R}^{H \times W \times 3} \rightarrow \mathbb{R}^{H \times W \times C} \end{equation}\]$\mathcal{E}$는 nearest-neighbor sampling을 통해 feature map을 원래 해상도로 업샘플링한다. ($C$는 feature 차원)
불확실성 예측
2D DINOv2 feature map을 얻으면 샘플링된 각 광선 $\textbf{r}$의 불확실성을 결정한다. 먼저 해당 feature \(\textbf{f} = \mathcal{F}_i (\textbf{r})\)을 쿼리한 다음 작은 MLP $G$에 입력하여 이 광선에 대한 불확실성을 추정한다.
\[\begin{equation} \beta (\textbf{r}) = G (\textbf{f}) \end{equation}\]불확실성 정규화
불확실성 예측에서 시공간적 일관성을 강화하기 위해 minibatch 내의 feature 벡터의 cosine similarity를 기반으로 하는 정규화 항을 도입한다. 구체적으로, 샘플링된 각 광선 $\textbf{r}$에 대해 동일한 batch의 광선으로 구성된 이웃 세트 $\mathcal{N}(\textbf{r})$을 정의한다. 이 이웃 세트는 threshold $\eta$를 충족하는 광선을 선택하여 형성된다.
\[\begin{equation} \mathcal{N} (\textbf{r}) = \{ \textbf{r}^\prime \vert \cos (\textbf{f}, \textbf{f}^\prime) > \eta \} \end{equation}\](\(\textbf{f}^\prime\)는 \(\textbf{r}^\prime\)의 feature)
광선 $\textbf{r}$에 대한 정제된 불확실성은 $\mathcal{N} (\textbf{r})$의 평균으로 계산된다.
\[\begin{equation} \bar{\beta} (\textbf{r}) = \frac{1}{\vert \mathcal{N} (\textbf{r}) \vert} \sum_{\textbf{r}^\prime \in \mathcal{N} (\textbf{r})} \beta (\textbf{r}^\prime) \end{equation}\]일관성을 강화하기 위해 불확실성의 분산에 페널티를 주는 정규화 항을 도입한다.
\[\begin{equation} \mathcal{L}_\textrm{reg} (\textbf{r}) = \frac{1}{\vert \mathcal{N} (\textbf{r}) \vert} \sum_{\textbf{r}^\prime \in \mathcal{N} (\textbf{r})} (\bar{\beta} (\textbf{r}) - \beta (\textbf{r}^\prime))^2 \end{equation}\]이 정규화는 이미지 전반의 유사한 feature를 갖는 광선들에서 불확실성 예측의 갑작스러운 변화를 완화하여, 불확실성 추정 과정의 전반적인 robustness와 일관성을 향상시키는 것을 목표로 한다.
2. Uncertainty for Distractor Removal in NeRF
저자들은 방해 요소와 상관관계가 있는 픽셀은 불확실성이 높고 정적 영역은 불확실성이 낮아야 한다고 가정하였다. 이 전제를 통해 예측된 불확실성을 NeRF의 loss function에 효과적으로 통합하여 점진적으로 방해 요소를 필터링하는 것을 목표로 한다.
먼저, NeRF의 loss function에 불확실성을 통합하는 고전적 방식의 잠재적 문제를 분석하고, 방해 요소를 robust하게 제거를 위해 불확실성을 통합하는 간단하면서도 효과적인 수정을 도입한다.
불확실성 수렴 분석
불확실성 예측은 다양한 분야에서 널리 사용되었다. 예를 들어, NeRF-W에서 loss는 다음과 같다.
\[\begin{equation} \mathcal{L} (\textbf{r}) = \frac{\| \textbf{C} (\textbf{r}) - \hat{\textbf{C}} (\textbf{r}) \|^2}{2 \beta (\textbf{r})^2} + \lambda_1 \log \beta (\textbf{r}) \end{equation}\]($\textbf{C} (\textbf{r})$는 GT 색상, $\hat{\textbf{C}} (\textbf{r})$는 렌더링된 색상)
불확실성 $\beta (\textbf{r})$은 가중치 함수로 처리된다. 정규화 항은 $\beta (\textbf{r}) = \infty$가 되는 것을 방지하는 데 중요하다.
Loss function에 대한 불확실성이 어떻게 변하는지 이해하기 위한 먼저 $\beta (\textbf{r})$에 대한 편미분을 구한다.
\[\begin{equation} \frac{\partial \mathcal{L}(\textbf{r})}{\partial \beta (\textbf{r})} = - \frac{\| \textbf{C} (\textbf{r}) - \hat{\textbf{C}} (\textbf{r}) \|^2}{\beta (\textbf{r})^3} + \lambda_1 \frac{1}{\beta (\textbf{r})} \end{equation}\]이 편미분이 0이 되는 최적의 불확실성에 대한 closed-form solution은 다음과 같다.
\[\begin{equation} \frac{\partial \mathcal{L}(\textbf{r})}{\partial \beta (\textbf{r})} = 0 \; \Rightarrow \; \beta (\textbf{r}) = \sqrt{\frac{1}{\lambda_1}} \| \textbf{C} (\textbf{r}) - \hat{\textbf{C}} (\textbf{r}) \| \end{equation}\]즉, 최적의 불확실성은 렌더링된 색상과 GT 색상 간의 오차에 비례한다.
그러나 $\ell_2$ loss를 사용할 때 문제가 발생한다. 특히 방해 요소와 배경의 색상이 가까우면 해당 영역의 불확실성 예측도 낮을 것이다. 이는 불확실성 기반 방해 요소 제거의 효과를 방해하고 렌더링된 이미지에 구름 아티팩트를 만든다.
불확실성 학습을 강화하기 위한 SSIM 기반 loss

SSIM은 휘도, 대비, 구조적 유사도로 구성된다. 이러한 구성 요소들은 장면 요소들을 구별하는 데 중요한 로컬한 구조 및 대비 차이를 포착한다. SSIM은 이 세 가지 요소를 함께 통합하여 방해 요소를 감지하는 데 효과적이다. SSIM loss는 다음과 같다.
$P$와 $\hat{P}$는 각각 GT 이미지와 렌더링된 이미지에서 샘플링한 패치이며, $L$, $C$, $S$는 각각 휘도, 대비, 구조적 유사도이다. 저자들은 위 식을 다음과 같이 수정하였다.
\[\begin{equation} \mathcal{L}_\textrm{SSIM} = (1 - L (P, \hat{P})) \cdot (1 - C (P, \hat{P})) \cdot (1 - S (P, \hat{P})) \end{equation}\]원래 SSIM loss와 비교했을 때, 수정된 SSIM loss는 동적 요소와 정적 요소 간의 차이에 더 큰 강조점을 둔다. 결과적으로 이 loss는 불확실성의 차이를 향상시켜 불확실성의 더 효과적인 최적화를 용이하게 한다.
이 수정된 SSIM loss를 기반으로 불확실성 학습에 맞춰진 새로운 loss를 도입한다.
\[\begin{equation} \mathcal{L}_\textrm{uncer} (\textbf{r}) = \frac{\mathcal{L}_\textrm{SSIM}}{2 \beta (\textbf{r})^2} + \lambda_1 \log \beta (\textbf{r}) \end{equation}\]\(\mathcal{L}_\textrm{uncer}\)는 불확실성 예측 MLP $G$를 학습시키는 데에만 적용된다. 이를 통해 NeRF 모델의 학습을 불확실성 예측에서 분리할 수 있으며, 이러한 분리는 학습된 불확실성이 다양한 유형의 방해 요소에 robustness를 보장한다.
3. Optimization
위에서 언급했듯이 불확실성 예측 모듈과 NeRF 모델을 별도로 최적화하는 것이 중요하다. 불확실성 예측 MLP를 최적화하기 위해 \(\mathcal{L}_\textrm{uncer}\)를 사용하고 정규화 항 \(\mathcal{L}_\textrm{reg} (\textbf{r})\)를 사용한다. 동시에, 다음 loss를 사용하여 NeRF 모델을 학습시킨다.
\[\begin{equation} \mathcal{L}_\textrm{nerf} (\textbf{r}) = \frac{\| \textbf{C} (\textbf{r}) - \hat{\textbf{C}} (\textbf{r}) \|^2}{2 \beta (\textbf{r})^2} \end{equation}\]\(\mathcal{L}_\textrm{uncer}\)가 이미 $\beta (\textbf{r}) = \infty$가 되는 것을 방지하기 때문에 이 loss는 정규화 항이 없다. 병렬 학습 프로세스는 \(\mathcal{L}_\textrm{uncer}\)에서 NeRF 표현으로, \(\mathcal{L}_\textrm{nerf}\)에서 MLP $G$로 gradient flow가 가지 못하게 막는다. 전체 loss는 모든 loss를 통합한 것이다.
\[\begin{equation} \lambda_2 \mathcal{L}_\textrm{nerf} (\textbf{r}) + \lambda_3 \mathcal{L}_\textrm{uncer} (\textbf{r}) + \lambda_4 \mathcal{L}_\textrm{reg} (\textbf{r}) \end{equation}\]추가로 NeRF 학습을 위해 Mip-NeRF 360의 interval loss와 distortion loss도 사용한다.
4. Dilated Patch Sampling
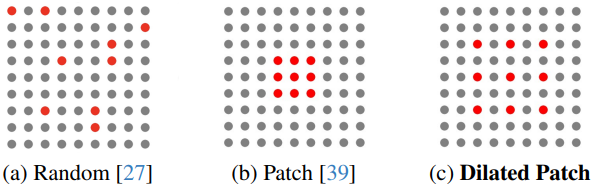
RobustNeRF는 패치 기반 광선 샘플링 (b)이 랜덤 샘플링 (a)보다 효과적임을 입증했다. 그러나 이 접근 방식에는 주로 샘플링된 패치의 크기가 작기 때문에 (ex. 16$\times$16) 한계가 있다. 특히 GPU 메모리의 제약으로 인해 batch size가 작은 경우 이 작은 컨텍스트는 방해 요소를 제거하기 위한 네트워크의 학습 용량을 제한하여 최적화 안정성과 수렴 속도에 영향을 미칠 수 있다.
이 문제를 해결하기 위해 dilated patch sampling (c)을 활용한다. 이 전략은 dilated patch에서 광선을 샘플링한다. 패치 크기를 확대함으로써 각 학습 iteration에서 사용 가능한 컨텍스트 정보의 양을 크게 늘릴 수 있다.
Experiments

저자들은 RobustNeRF 데이터셋과 함께 자체 제작한 On-the-go 데이터셋을 사용하였다. 위는 학습 이미지의 예시들이다.
1. Evaluation
다음은 On-the-go 데이터셋에 대한 novel view synthesis (NVS) 성능을 비교한 결과이다.
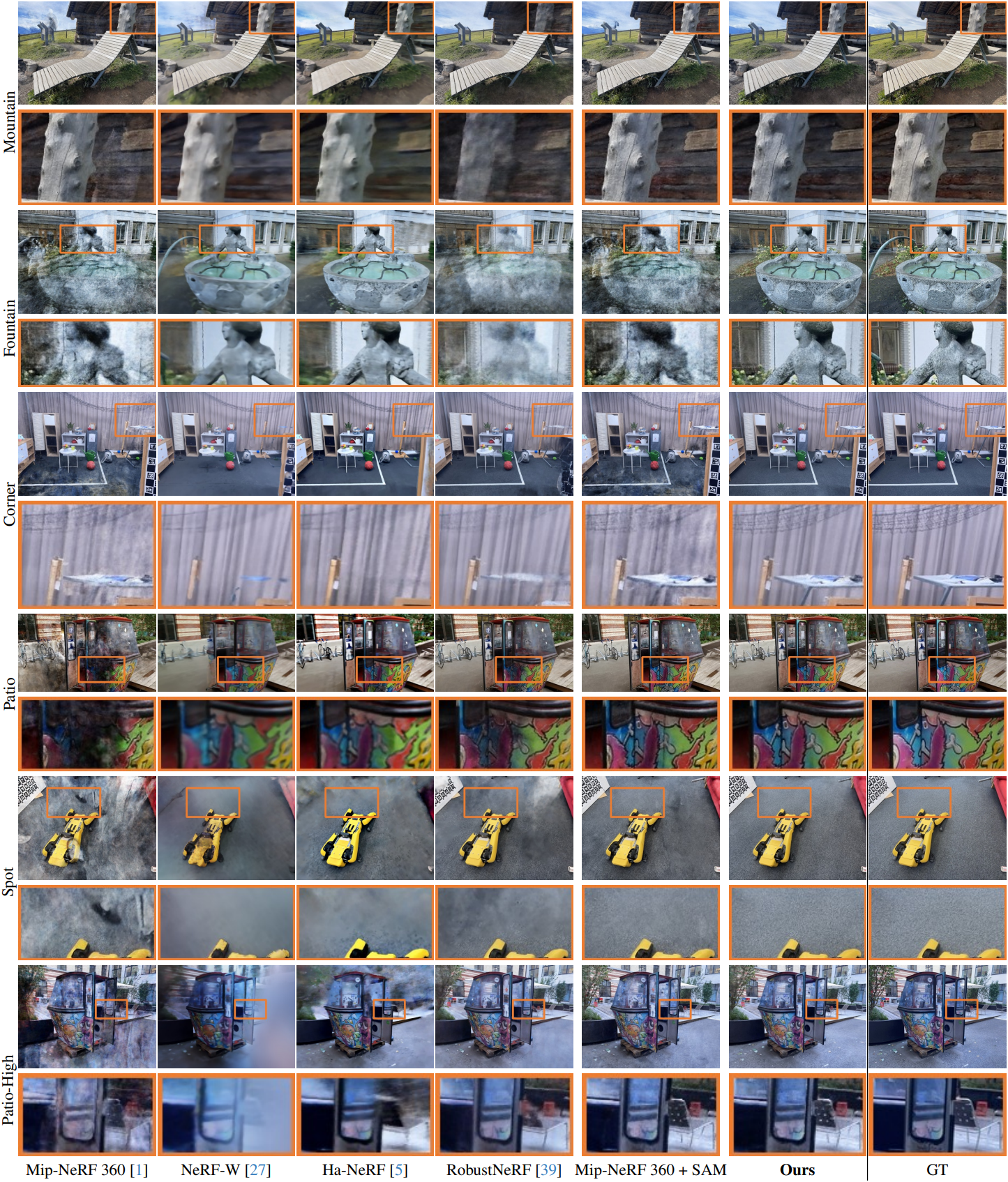

다음은 RobustNeRF 데이터셋에 대한 novel view synthesis (NVS) 성능을 비교한 결과이다.

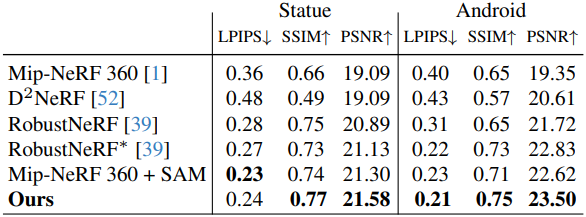
2. Ablation Study
다음은 patch dilation rate에 대한 ablation 결과이다.
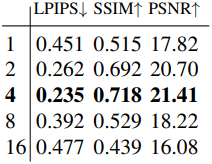
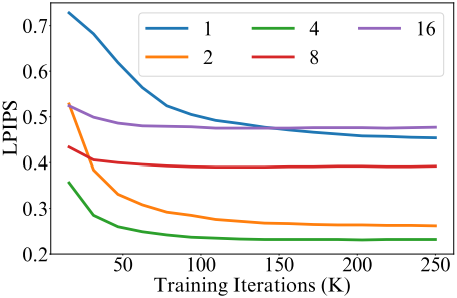
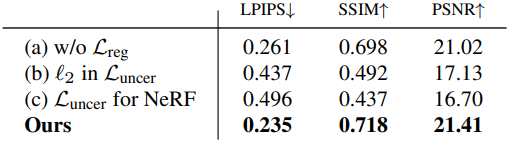
다음은 loss function에 대한 ablation 결과이다.

3. Analysis
다음은 RobustNeRF와 수렴 속도를 비교한 결과이다.

다음은 정적 장면에 대한 성능을 비교한 것이다.

다음은 큰 방해 요소를 다루는 예시들이다.
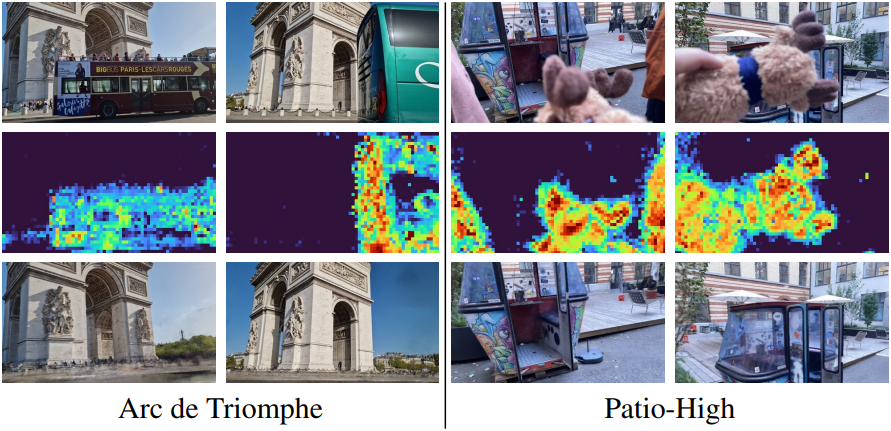
Limitation
창문이나 금속과 같은 반사되는 표면과 같이 강한 view-dependent 효과가 있는 영역에 대한 정확한 불확실성을 예측하는 데 어려움을 겪는다.