[논문리뷰] NeRF-Casting: Improved View-Dependent Appearance with Consistent Reflections

SIGGRAPH Asia 2024. [Paper] [Page]
Dor Verbin, Pratul P. Srinivasan, Peter Hedman, Ben Mildenhall, Benjamin Attal, Richard Szeliski, Jonathan T. Barron
Google | Carnegie Mellon University
23 May 2024

Introduction

NeRF는 신경망을 사용하여 3D 장면의 geometry와 색상을 표현하여, 관찰되지 않은 새로운 장면을 렌더링하는 것을 목표로 한다. 최근 NeRF 방법은 큰 MLP를 voxel grid와 유사한 데이터 구조 또는 grid와 작은 MLP의 조합으로 대체하여 NeRF의 효율성을 높이는 데 중점을 두고 있다. 이러한 방법을 통해 NeRF는 세부적인 대규모 장면을 표현할 수 있도록 확장할 수 있었지만, 그 이점은 3D geometry와 주로 diffuse color에 국한되었다.

NeRF가 view-dependent한 사실적인 외형을 모델링하는 능력을 확장하는 것은 여전히 ​​어려운 과제이다. SOTA 모델은 두 가지 측면에서 한계가 있다.

1. 먼 거리의 environment illumination에 대한 정확한 반사만 합성할 수 있고, 근처 장면 콘텐츠의 설득력 있는 반사를 렌더링하는 데 어려움을 겪는다.
2. 특정 지점에서 view-dependent한 outgoing radiance를 표현하기 위해 큰 MLP에 의존하고, 세부적인 반사를 포함하는 더 큰 실제 장면으로 확장하는 데 어려움을 겪는다.

본 논문은 NeRF 렌더링 모델에 ray tracing을 도입하여 이 두 가지 문제를 모두 해결하는 접근법을 제시하였다. 카메라 광선을 따라 각 지점의 view-dependent한 외형을 얻기 위해 큰 MLP를 쿼리하는 대신, 본 방법은 이러한 지점에서 반사 광선을 geometry로 투사하고, 반사된 장면 콘텐츠에서 적절하게 앤티앨리어싱된 feature를 샘플링한 후, 작은 MLP를 사용하여 이러한 feature를 반사 색상으로 디코딩한다. 복구된 NeRF에 ray casting을 하면 가깝고 먼 콘텐츠의 일관된 반사가 자연스럽게 합성된다. 또한, ray tracing을 통해 외형을 계산하면 장면의 각 지점에서 매우 세부적인 view-dependent한 함수를 큰 MLP로 표현하는 부담을 줄일 수 있다.

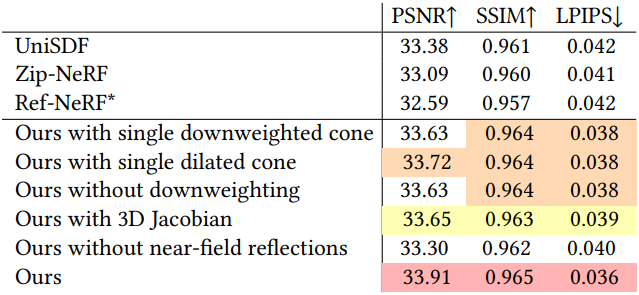
본 논문의 NeRF-Casting은 NeRF의 view-dependent한 외형을 개선하는 데 있어 이전 방법들보다 효율적이며, 특히 가까운 콘텐츠에 대한 더 높은 품질의 반사를 렌더링한다.

Method

저자들은 세 가지 목표를 염두에 두고 방법을 설계했다.

1. 계산량이 많은 MLP 계산에 의존하지 않고 정확하고 세부적인 반사를 모델링한다.
2. 적은 수의 반사 광선만 투사한다.
3. 이러한 반사 광선을 따라 각 지점에서 표현을 쿼리하는 데 필요한 계산을 최소화한다.

3D volume density와 feature 표현은 Zip-NeRF를 기반으로 한다. Zip-NeRF는 멀티스케일 해시그리드를 사용하여 3D feature를 저장하고, 작은 MLP(레이어 1개, 너비 64)를 사용하여 feature를 density로 디코딩하며, 더 큰 MLP(레이어 3개, 너비 256)를 사용하여 feature를 색상으로 디코딩한다. 즉, 광선을 따라 샘플의 density와 feature를 쿼리하는 것이 색상을 평가하는 것보다 저렴하다. 본 논문은 이러한 제약 조건을 고려하여 반사광을 렌더링하기 위한 다음과 같은 절차를 제안하였다.

1. 각 카메라 광선을 따라 volume density를 쿼리하여 광선의 예상 종료 지점과 표면 normal을 계산한다.
2. 반사 방향과 예상 종료 지점에 따라 반사 원뿔을 투사한다.
3. 작은 MLP를 사용하여 누적된 reflection feature를 다른 샘플링된 값 (ex. diffuse color feature, 블렌딩 가중치)과 결합하여 광선을 따라 각 샘플에 대한 색상 값을 생성한다.
4. 이러한 샘플과 density를 알파 블렌딩하여 최종 색상을 만든다.

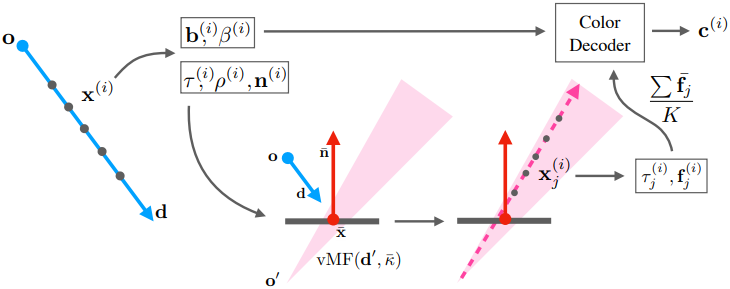
1. Reflection Cone Tracing

원점 $\textbf{o}$와 방향 $\textbf{d}$를 갖는 주어진 광선에 대해, 광선을 따라 $N$개의 점 \(\{\textbf{x}^{(𝑖)}\}_{i=1}^N\)을 샘플링하고, NeRF를 계산하여 표면 normal과 같은 3D 값들을 얻는다. 그런 다음, 이러한 값들을 알파 블렌딩하여 종료 지점 $\bar{\textbf{x}}$와 표면 normal $\bar{\textbf{n}}$을 구한다.

\[\begin{equation} \bar{\textbf{x}} = \sum_{i=1}^N w^{(i)} \textbf{x}^{(i)}, \quad \bar{\textbf{n}} = \sum_{i=1}^N w^{(i)} \textbf{n}^{(i)} \\ \textrm{where} \quad w^{(i)} = (1 - \exp(-\tau^{(i)} (t^{(i+1)} - t^{(i)}))) \exp \left( - \sum_{j < i} \tau^{(j)} (t^{(j+1)} - t^{(j)}) \right) \end{equation}\]

그런 다음, 초기 광선을 표면 normal에 대해 반사하여 방향 $\textbf{d}^\prime$를 갖는 새로운 반사 광선을 구성한다.

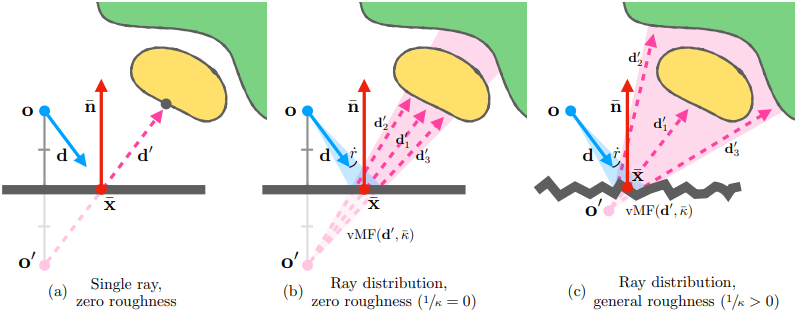
\[\begin{equation} \textbf{d}^\prime = \textbf{d} - 2(\bar{\textbf{n}} \cdot \textbf{d}) \bar{\textbf{n}} \end{equation}\]

반사 광선을 하나만 사용하는 것은 완벽한 거울이 아닌 material을 렌더링하는 데 사용할 수 없으며 Zip-NeRF가 각 픽셀에 대해 광선 대신 원뿔을 추적한다는 사실을 무시한다. 따라서 반사 광선의 원뿔형 분포를 모델링한다. 이 분포의 모양은 두 가지 요인의 영향을 받는다.

1. 카메라에서 투사된 원래 픽셀 원뿔의 반경
2. 카메라 광선의 예상 종료 지점에서 표면의 roughness

먼저 반사 광선의 원뿔형 분포와 표면 거칠기로 인한 반사 방향의 분포를 거울 반사 방향 d′를 중심으로 하는 von Mises-Fisher (vMF) 분포, 즉 정규화된 spherical Gaussian 분포로 모델링한다. 카메라 광선의 예상 종료 지점에서 반사된 광선 원뿔은 vMF 분포 $\textrm{vMF}(\textbf{d}^\prime, \bar{\kappa})$로 모델링되며, 픽셀 원뿔 분포에 대한 vMF 너비 $1/\kappa$는 픽셀 광선 원뿔의 반경 $\dot{r}$과 primary ray에 따라 합성된 roughness의 합이다.

\[\begin{equation} \bar{\kappa}^{-1} = \dot{r} + \bar{\rho} \end{equation}\]

표면에서 반사된 광선 원뿔의 단면이 입사 광선의 단면과 일치하도록 하기 위해, 반사 광선 원뿔의 원점에 roughness-dependent shift를 적용하여 입사 광선의 반지름이 \(\dot{r} \| \textbf{o} - \bar{\textbf{x}} \|\)가 되도록 한다.

\[\begin{equation} \textbf{o}^\prime = \bar{\textbf{x}} - \| \textbf{o} - \bar{\textbf{x}} \| \frac{\dot{r}}{\dot{r} + \bar{\rho}} \textbf{d}^\prime \end{equation}\]

누적된 roughness $\bar{\rho}$가 0일 때 $\textbf{o}^\prime$은 표면의 반대쪽에 완벽하게 미러링된다.

2. Conical Reflected Features

반사 광선에 대한 vMF 분포를 정의했으므로, vMF 분포에 대한 볼륨 렌더링된 feature 기댓값을 추정하여 반사된 색상으로 디코딩하는 것이다.

\[\begin{equation} \bar{\textbf{f}}^\ast = \mathbb{E}_{\boldsymbol{\omega} \sim \textrm{vMF}(\textbf{d}^\prime, \bar{\kappa})} [\bar{\textbf{f}}(\boldsymbol{\omega})] = \int_{\mathbb{S}^2} \bar{\textbf{f}}(\boldsymbol{\omega}) \textrm{vMF}(\boldsymbol{\omega}; \textbf{d}^\prime, \bar{\kappa}) d \boldsymbol{\omega} \end{equation}\]

(\(\bar{\textbf{f}}(\boldsymbol{\omega})\)는 \(\boldsymbol{\omega}\) 방향으로 누적된 feature 벡터)

랜덤하게 샘플링된 광선에 대해 몬테카를로 적분을 수행하는 것은 각 샘플이 광선을 따라 볼륨 렌더링을 필요로 하기 때문에 엄청나게 비싸다. 저자들은 Zip-NeRF에서 영감을 받아, feature downweighting과 결합된 소수의 대표 샘플 집합을 사용하여 이 적분을 근사하였다. 그러나 Zip-NeRF와 달리, 이 두 연산을 3D 유클리드 공간이 아닌 2D 방향 도메인에서 수행한다.

Directional Sampling

많은 수의 랜덤 반사 광선을 샘플링하는 대신, unscented directional sampling을 사용하여 $K$개의 광선을 선택한다 (실험에서는 $K = 5$). 구체적으로, 평균이 $\textbf{d}^\prime$과 $\bar{\kappa}$로 유지되도록 하기 위해, \(\textbf{d}_1^\prime = \textbf{d}^\prime\)로 설정하고, \(\{\textbf{d}_j^\prime\}_{j=2}^K\)는 반지름이 $\bar{\kappa}$에 따라 달라지는 \(\textbf{d}^\prime\) 주변의 원에 배치한다. 최적화 과정에서는 원 위에서 샘플을 랜덤하게 회전시키고, 평가 과정에서는 고정한다.

샘플링된 각 광선 \((\textbf{o}_j^\prime, \textbf{d}_j^\prime)\)에 대해 광선을 따라 $N^\prime$개의 포인트를 샘플링하고 해당 포인트에서 volume density와 feature를 평가하고, 이를 feature \(\bar{\textbf{f}} (\textbf{d}_j^\prime)\)으로 볼륨 렌더링한다. 그런 다음 $K$개의 feature를 평균화하여 반사 원뿔에 대한 하나의 feature 벡터를 생성한다.

\[\begin{equation} \bar{\textbf{f}} (\textbf{d}_j^\prime) = \sum_{i=1}^{N^\prime} w_j^{(i)} \textbf{f}(x_j^{(i)}), \quad \textbf{f} = \frac{1}{K} \sum_{j=1}^K \bar{\textbf{f}} (\textbf{d}_j^\prime) \end{equation}\]

Reflection Feature Downweighting

Directional sampling은 평균을 취할 적은 수의 대표 광선 집합을 선택하는 데 도움이 된다. 그러나 roughness가 높은 표면의 경우, 샘플링된 광선이 3D grid 셀에 비해 서로 떨어져 있을 수 있다. 즉, 위 식의 feature가 앨리어싱될 수 있으며, 반사된 광선 방향의 작은 변화도 외형에 큰 변화를 초래할 수 있다.

이를 방지하기 위해 Zip-NeRF의 “feature downweighting”을 적용한다. vMF 원뿔에 비해 작은 voxel에 해당하는 feature에 작은 multiplier를 곱하여 렌더링 색상에 미치는 영향을 줄인다. Zip-NeRF를 따라, 점 $\textbf{x}$에서 downweighting된 feature를 다음과 같이 정의한다.

\[\begin{equation} \textbf{f}_\textrm{aa}(\textbf{x}) = \textrm{erf} \left( \left( \sqrt{8} \boldsymbol{\nu} \sigma (\textbf{x}) \right)^{-1} \right) \odot \textbf{f}(\textbf{x}) \end{equation}\]

($\sigma (\textbf{x})$는 $\textbf{x}$에서의 원뿔의 스칼라 스케일, $\boldsymbol{nu}$는 NGP grid 해상도의 스케일을 나타내는 $\textbf{f}$와 동일한 차원의 벡터, $\odot$은 element-wise multiplication)

큰 장면의 경우 contraction function $C$를 사용해야 하기 때문에, $C$의 비선형 영역에서 $\sigma (\textbf{x})$의 동작을 고려하는 것이 특히 중요하다.

\[\begin{equation} C(\textbf{x}) = \begin{cases} \textbf{x} & \textrm{if} \; \| \textbf{x} \| \le 1 \\ \left( 2 - \frac{1}{\| \textbf{x} \|} \right) \frac{\textbf{x}}{\| \textbf{x} \|} & \textrm{if} \; \| \textbf{x} \| > 1 \end{cases} \end{equation}\]

Zip-NeRF는 $\sigma (\textbf{x})$를 contraction function $C$의 3D Jacobian의 eigenvalue들의 기하 평균으로 스케일링한다. 하지만 $C$가 원점 쪽으로 먼 점들을 강하게 수축시키기 때문에, 원점에서 멀리 떨어진 점에 대해서는 $\sigma (\textbf{x})$가 0에 가까워지는, 즉 downweighting이 적용되지 않는 결과가 발생한다. 결과적으로 ZipNeRF의 downweighting 함수를 사용하면 먼 콘텐츠의 반사에 상당한 앨리어싱이 발생한다.

따라서 2D 방향 도메인에 제한된 Jacobian을 사용하고 다음과 같이 $\sigma (\textbf{x})$를 정의한다.

\[\begin{aligned} \sigma (\textbf{x}) &= \gamma \cdot (\dot{r} + \bar{\rho}) \| \textbf{x} - \textbf{o}^\prime \| \sqrt{\textrm{det} \textbf{J}_C^\textrm{dir} (\textbf{x})} \\ &= \gamma \cdot (\dot{r} + \bar{\rho}) \| \textbf{x} - \textbf{o}^\prime \| \sqrt{\textrm{det} \textbf{J}_C (\textbf{x}) \cdot \left( \frac{\partial}{\partial \| \textbf{x} \|} \left( C(\textbf{x}) \cdot \frac{\textbf{x}}{\| \textbf{x} \|} \right) \right)^{-1}} \\ &= \gamma \cdot (\dot{r} + \bar{\rho}) \| \textbf{x} - \textbf{o}^\prime \| \cdot \frac{2 \max (1, \| \textbf{x} \|) - 1}{\max (1, \| \textbf{x} \|)^2} \end{aligned}\]

($\gamma$는 모든 실험에서 16으로 설정한 고정된 스케일 배수)

$\textbf{x}$가 원점에서 멀리 떨어져 있을 때, $\sigma (\textbf{x})$는 $2 \gamma (\dot{r} + \bar{\rho})$에 접근한다. 이는 Zip-NeRF의 스케일과는 대조적이다. Zip-NeRF의 스케일은 0에 가까워서 원거리 콘텐츠의 가중치를 낮추지 않는다. 원거리 조명의 반사에 대한 앨리어싱을 방지하기 위해서는 원거리 콘텐츠의 가중치를 적절히 낮추는 것이 중요하다.

3. Color Decoder

색상 디코더의 역할은 광선을 따라 샘플링된 모든 지점에 색상을 할당하는 것이다. UniSDF에서 영감을 받은 이 색상 디코더는 두 가지 색상을 결합하여 사용한다.

\[\begin{equation} \textbf{c} (\textbf{x}^{(i)}, \textbf{d}) = \beta^{(i)} \textbf{c}_v (\textbf{x}^{(i)}, \textbf{d}) + (1 - \beta^{(i)}) \textbf{c}_r (\textbf{x}^{(i)}, \textbf{d}^\prime) \end{equation}\]

($\beta^{(i)} \in [0, 1]$는 sigmoid가 적용된 geometry 인코더의 출력 가중치 계수)

\(\textbf{c}_v\)는 일반적인 NeRF의 view-dependent한 외형 모델과 유사하며, \(\textbf{c}_r\)은 광택이 있는 외형을 모델링하기 위해 설계되었다.

\[\begin{aligned} \textbf{c}_v (\textbf{x}^{(i)}, \textbf{d}) &= g(\textbf{x}^{(i)}, \textbf{b}^{(i)}, \textbf{n}^{(i)}, \textbf{d}) \\ \textbf{c}_r (\textbf{x}^{(i)}, \textbf{d}^\prime) &= h(\textbf{x}^{(i)}, \textbf{b}^{(i)}, \textbf{n}^{(i)}, \textbf{d} \cdot \textbf{n}^{(i)}, \textbf{d}^\prime, \bar{\textbf{f}}) \end{aligned}\]

($g$와 $h$는 MLP, $\textbf{b}$는 geometry feature를 MLP에 넣어 얻은 bottleneck 벡터)

UniSDF와 달리, $\beta$를 이미지 공간이 아닌 3D 공간에 적용하므로 $\bar{\textbf{f}}$가 카메라 광선을 따라 모든 샘플에서 색상 디코더에 입력된다. 최적화 초기, geometry가 아직 흐릿할 때 광선을 따라 모든 지점이 $\bar{\textbf{f}}$를 활용할 수 있기 때문에 이 방식이 더 수렴에 유용하다.

4. Geometry Representation and Regularization

본 논문의 geometry 표현은 Zip-NeRF의 표현 방식을 기반으로 한다. Ref-NeRF와 마찬가지로, normal에 orientation loss를 적용하고, NGP feature에 적용된 작은 MLP가 예측한 normal $\tilde{\textbf{n}}$을 활용한다. Ref-NeRF와 달리, 비대칭적인 normal loss를 사용하는데, 이는 $\textbf{n}$에서 $\tilde{\textbf{n}}$으로 흐르는 gradient와 $w$에서 $\tilde{\textbf{n}}$으로 흐르는 gradient에 대한 별도의 가중치를 허용하며, 그 반대의 경우도 마찬가지이다.

\[\begin{equation} \mathcal{L}_\textrm{pred} = \lambda_{\textbf{n}} \mathcal{L}_p (w, \textbf{n}, \textrm{sg}(\tilde{\textbf{n}})) + \lambda_{\tilde{\textbf{n}}} \mathcal{L}_p (\textrm{sg}(w), \textrm{sg}(\textbf{n}), \tilde{\textbf{n}}) \\ \textrm{where} \quad \mathcal{L}_p (w, \textbf{n}, \tilde{\textbf{n}}) = \sum_{i=1}^N w^{(i)} \| \textbf{n}^{(i)} - \tilde{\textbf{n}}^{(i)} \|^2 \end{equation}\]

($\textrm{sg}(\cdot)$는 stop-gradient 연산, \(\lambda_{\textbf{n}} = 10^{-3}\), \(\lambda_{\tilde{\textbf{n}}} = 0.3\))

이를 통해 예측된 normal을 NeRF의 density에 해당하는 normal과 강력하게 연결하면서도 geometry를 과도하게 매끄럽게 만들지 않는다. 이를 통해 예측된 normal은 geometry normal과 유사하면서도 훨씬 더 매끄러워지므로, 반사 방향을 계산하고 정확한 specular highlight를 생성하는 데 유용하다.

Experiments