[논문리뷰] NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

ECCV 2020. [Paper] [Page] [Github] [Data]
Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, Ren Ng
UC Berkeley | Google Research | UC San Diego
19 Mar 2020

Introduction

본 논문에서는 캡처된 이미지 세트를 렌더링하는 오차를 최소화하기 위해 연속적인 5D 장면 표현의 파라미터를 직접 최적화하여 뷰 합성의 오랜 문제를 새로운 방식으로 해결하였다.

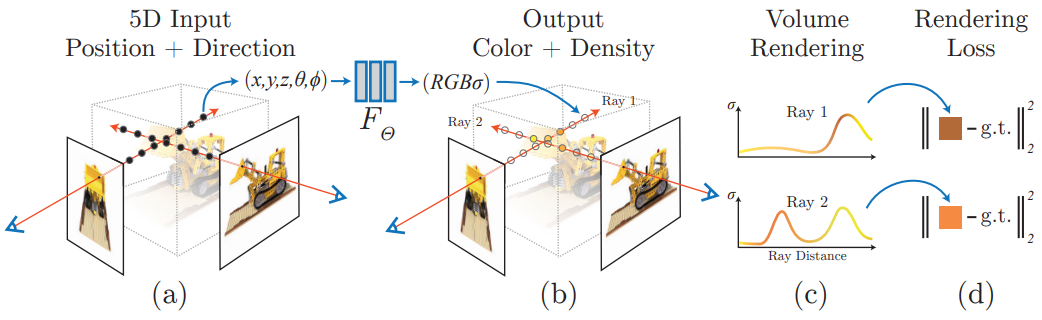
정적 장면을 공간의 각 지점 $(x, y, z)$에서 각 방향 $(\theta, \phi)$로 방출되는 광도(radiance)와 각 지점의 밀도를 출력하는 연속적인 5D 함수로 표현한다. 여기서 밀도는 얼마나 많은 광도가 $(x, y, z)$를 통과하는 광선에 의해 누적되는지를 제어하는 미분 가능한 투명도의 역할을 한다. 본 논문의 방법은 convolutional layer를 사용하지 않고 MLP만을 사용하여 이 함수를 표현하며, 하나의 5D 좌표 $(x, y, z, \theta, \phi)$에서 하나의 밀도와 뷰에 따른 RGB 색상으로 회귀하여 최적화한다. 특정 시점에서 이 neural radiance field (NeRF)를 렌더링하기 위해 다음을 수행한다.

1. 광선을 따라 이동하여 샘플링된 3D 포인트 집합을 생성
2. 해당 점들과 각 점에 대한 2D 시점 방향을 신경망에 대한 입력을 사용하여 색상과 밀도의 집합을 생성
3. 고전적인 볼륨 렌더링 기술을 사용하여 해당 색상과 밀도를 2D 이미지에 집계

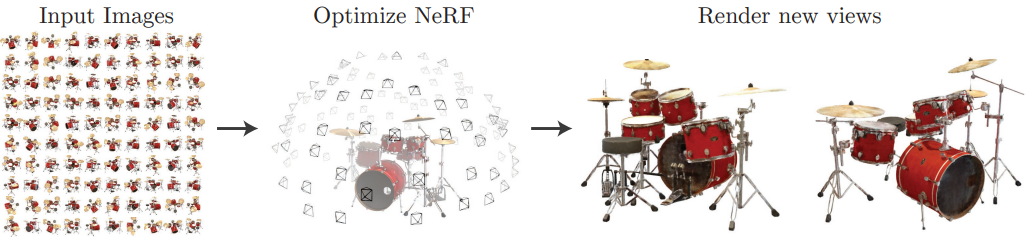
이 프로세스는 미분 가능하기 때문에 경사하강법(gradient descent)을 사용하여 관찰된 각 이미지와 렌더링된 해당 뷰 사이의 오차를 최소화하여 모델을 최적화할 수 있다. 여러 뷰에서 이 오차를 최소화하면 신경망이 실제 기본 장면 콘텐츠가 포함된 위치에 높은 밀도와 정확한 색상을 할당하여 장면의 일관된 모델을 예측할 수 있다. 전체 파이프라인은 아래 그림과 같다.

저자들은 복잡한 장면에 대한 NeRF 표현을 최적화하는 기본 구현이 충분히 높은 해상도의 표현으로 수렴되지 않으며 카메라 광선당 필요한 샘플 수가 비효율적이라는 것을 발견했다. 저자들은 MLP가 더 높은 주파수의 함수를 나타낼 수 있도록 하는 위치 인코딩으로 입력 5D 좌표를 변환하여 이러한 문제를 해결하고, 이 고주파수의 장면 표현을 적절하게 샘플링하는 데 필요한 쿼리 수를 줄이기 위한 계층적 샘플링 절차를 제안하였다.

본 논문의 접근 방식은 volumetric 표현의 이점을 상속한다. 둘 다 복잡한 실제 형상과 모양을 표현할 수 있으며 투영된 이미지를 사용하는 기울기 기반 최적화에 매우 적합하다. 결정적으로, 본 논문의 방법은 고해상도에서 복잡한 장면을 모델링할 때 이산화된 복셀 그리드의 엄청난 저장 비용을 극복한다.

Neural Radiance Field Scene Representation

입력이 3D 위치 $\mathbf{x} = (x, y, z)$와 2D 시점 방향 $(\theta, \phi)$이고 출력이 색상 $\mathbf{c} = (r, g, b)$와 밀도 $\sigma$인 5D 벡터 값 함수로 연속적인 장면을 나타낸다. 실제로 방향을 3D Cartesian 단위 벡터 $\mathbf{d}$로 표현한다. MLP 네트워크 $F_\Theta : (\mathbf{x}, \mathbf{d}) \rightarrow (\mathbf{c}, σ)$를 사용하여 이 연속적인 5D 장면 표현을 근사화하고 가중치 $\Theta$를 최적화하여 각 입력 5D 좌표에서 밀도와 색상으로 매핑한다.

네트워크가 위치 $x$의 함수로 밀도 $\sigma$를 예측하도록 제한하고 RGB 색상 $\mathbf{c}$가 위치와 시점 방향 모두의 함수로 예측되도록 하여 표현이 멀티뷰 일관성을 갖도록 권장한다. 이를 위해 MLP $F_\Theta$는 먼저 8개의 fully-connected layer (ReLU와 레이어당 256개 채널 사용)로 입력 3D 좌표 $\mathbf{x}$를 처리하고 $\sigma$와 256차원 feature 벡터를 출력한다. 그런 다음 이 feature 벡터는 카메라 광선의 시점 방향과 concatenate되어 뷰에 따른 RGB 색상을 출력하는 하나의 추가 fully-connected layer (ReLU와 128개 채널 사용)로 전달된다.

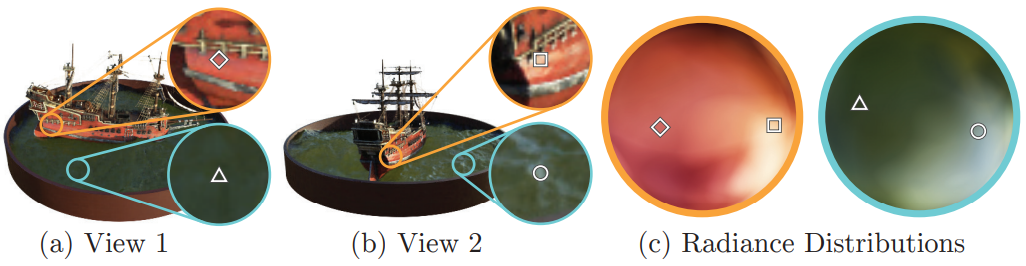
위 그림은 입력 뷰 방향을 사용하여 non-Lambertian effect를 표현하는 방법에 대한 예시이다.

위 그림에서 볼 수 있듯이 뷰 의존성 없이 학습된 모델 (입력으로 $\mathbf{x}$만)은 반사를 표현하는 데 어려움이 있다.

Volume Rendering with Radiance Fields

본 논문의 5D NeRF 표현은 공간의 모든 지점에서 밀도와 광도(radiance)로 장면을 나타낸다. 저자들은 고전적인 볼륨 렌더링의 원리를 사용하여 장면을 통과하는 모든 광선의 색상을 렌더링한다. 밀도 $\sigma(\mathbf{x})$는 광선이 위치 $\mathbf{x}$의 극소 입자에서 끝나는 미분 확률로 해석될 수 있다. Near bound $t_n$과 far bound $t_f$를 갖는 카메라 광선 $\mathbf{r}(t) = \mathbf{o} + t\mathbf{d}$의 예상 색상 $C(\mathbf{r})$은 다음과 같다.

\[\begin{equation} C(\mathbf{r}) = \int_{t_n}^{t_f} T(t) \sigma (\mathbf{r} (t)) \mathbf{c} (\mathbf{r} (t), \mathbf{d}) dt \quad \textrm{where} \quad T(t) = \exp \bigg( - \int_{t_n}^t \sigma (\mathbf{r} (s)) ds \bigg) \end{equation}\]

함수 $T(t)$는 $t_n$에서 $t$까지 광선을 따라 누적된 투과율, 즉 광선이 다른 입자에 부딪히지 않고 $t_n$에서 $t$로 이동할 확률을 나타낸다. 연속적인 NeRF에서 뷰를 렌더링하려면 원하는 가상 카메라의 각 픽셀을 통해 추적되는 카메라 광선에 대해 이 적분 $C(\mathbf{r})$을 추정해야 한다.

구적법(quadrature)을 사용하여 이 연속적인 적분을 수치적으로 추정한다. 일반적으로 이산화된 복셀 그리드를 렌더링하는 데 사용되는 결정론적 구적법은 MLP가 고정된 이산 위치 집합에서만 쿼리되기 때문에 표현의 해상도를 효과적으로 제한한다. 대신, 저자들은 $N$개의 균일한 간격의 bin으로 분할한 다음 각 bin 내에서 하나의 샘플을 무작위로 추출하는 계층화된 샘플링 접근 방식을 사용하였다.

\[\begin{equation} t_i \sim \mathcal{U} \bigg[ t_n + \frac{i-1}{N} (t_f - t_n), \, t_n + \frac{i}{N} (t_f - t_n) \bigg] \end{equation}\]

적분 값을 추정하기 위해 샘플들의 이산적인 집합을 사용하지만 계층화된 샘플링을 사용하면 최적화 과정에서 연속적인 위치에서 MLP가 평가되므로 연속적인 장면 표현을 나타낼 수 있다. 이러한 샘플들을 사용하여 다음과 같이 $C(\mathbf{r})$을 추정한다.

\[\begin{equation} \hat{C}(\mathbf{r}) = \sum_{i=1}^N T_i (1 - \exp (-\sigma_i \delta_i)) c_i \quad \textrm{where} \quad T_i = \exp \bigg( -\sum_{j=1}^{i-1} \sigma_j \delta_j \bigg) \end{equation}\]

여기서 $\delta_i = t_{i+1} − t_i$는 인접한 샘플 사이의 거리이다. $(c_i, \sigma_i)$ 값 집합에서 $\hat{C} (\mathbf{r})$을 계산하기 위한 이 함수는 간단하게 미분 가능하며 알파 값 $\alpha_i = 1 − \exp(−\sigma_i \delta_i)$를 사용한 전통적인 알파 합성이 된다.

Optimizing a Neural Radiance Field

본 논문은 고해상도의 복잡한 장면을 표현할 수 있도록 두 가지 개선 사항을 도입하였다. 첫 번째는 MLP가 고주파 함수를 나타내는 데 도움이 되는 입력 좌표의 위치 인코딩이고, 두 번째는 이 고주파 표현을 효율적으로 샘플링할 수 있는 계층적 샘플링 절차이다.

1. Positional encoding

저자들은 신경망 $F_\Theta$가 $xyz \theta \phi$ 좌표에서 직접 연산하도록 하면 색상과 형상의 고주파 변화를 나타내는 렌더링 성능이 좋지 않다는 것을 발견했다. 이는 On the spectral bias of neural networks 논문의 결과와 동일하다. 해당 논문은 신경망이 저주파 함수를 학습하는 쪽으로 편향되어 있음을 보여주었다. 또한 입력을 신경망에 전달하기 전에 고주파 함수를 사용하여 더 높은 차원 공간에 입력을 매핑하면 고주파 변화가 포함된 데이터를 더 잘 피팅할 수 있음을 보여주었다.

저자들은 이러한 발견을 활용하고 $F_\Theta$를 두 함수 $F_\Theta = F_\Theta^\prime \circ \gamma$의 구성 (하나는 학습되고 하나는 학습되지 않음)으로 재구성하면 성능이 크게 향상된다. 여기서 $\gamma$는 $\mathbb{R}$에서 더 높은 차원 공간인 $\mathbb{R}^{2L}$로의 매핑이고 $F_\Theta^\prime$은 여전히 단순하게 일반 MLP이다. 사용하는 인코딩 함수는 다음과 같다.

\[\begin{equation} \gamma(p) = (\sin(2^0 \pi p), \cos(2^0 \pi p), \cdots, \sin(2^{L-1} \pi p), \cos(2^{L-1} \pi p)) \end{equation}\]

$\gamma(\cdot)$는 $\mathbf{x}$의 3개 좌표 값 ($[-1, 1]$로 정규화됨) 각각과 Cartesian 시점 방향 단위 벡터 $\mathbf{d}$의 세 성분에 개별적으로 적용된다. 저자들은 실험에서 $\gamma(\mathbf{x})$에 대해 $L = 10$, $\gamma(\mathbf{d})$에 대해 $L = 4$로 설정했다.

유사한 매핑이 Transformer 아키텍처에서 사용되는데, 이를 위치 인코딩이라고 한다. 그러나 Transformer는 순서 개념이 포함되지 않은 아키텍처에 대한 입력으로 시퀀스에서 토큰의 이산적인 위치를 제공하려는 다른 목표를 위해 이를 사용한다. 대조적으로, 본 논문은 이러한 함수를 사용하여 연속적인 입력 좌표를 더 높은 차원 공간에 매핑하여 MLP가 더 높은 주파수의 함수에 더 쉽게 접근할 수 있도록 한다.

2. Hierarchical volume sampling

각 카메라 광선을 따라 $N$개의 쿼리 지점에서 NeRF 신경망을 조밀하게 평가하는 렌더링 전략은 비효율적이다. 렌더링된 이미지에 기여하지 않는 여유 공간과 가려지는 영역은 여전히 반복적으로 샘플링된다. 저자들은 볼륨 렌더링의 초기 연구에서 영감을 얻고 최종 렌더링에 대한 예상 효과에 비례하여 샘플을 할당하여 렌더링 효율성을 높이는 계층적 표현을 제안하였다.

장면을 표현하기 위해 하나의 신경망을 사용하는 대신, “coarse” 네트워크와 “fine” 네트워크 두 개를 동시에 최적화한다. 먼저 계층화된 샘플링을 사용하여 일련의 $N_c$개의 위치를 샘플링하고 이러한 위치에서 coarse 네트워크를 평가한다. 이 coarse 네트워크의 출력을 바탕으로 샘플이 물체의 관련된 부분으로 편향되는 각 광선을 따라 더 많은 정보에 기반한 포인트 샘플링을 생성한다. 이를 위해 먼저 coarse 네트워크 $\hat{C}_c (\mathbf{r})$의 알파 합성 색상을 광선을 따라 샘플링된 모든 색상 $c_i$의 가중 합으로 다시 쓴다.

\[\begin{equation} \hat{C}_c (\mathbf{r}) = \sum_{i=1}^{N_c} w_i c_i, \quad w_i = T_i (1 - \exp (-\sigma_i \delta_i)) \end{equation}\]

이러한 가중치를 \(\hat{w}_i = w_i / \sum_{j=1}^{N_c} w_j\)로 정규화하면 광선을 따라 부분적으로 일정한 확률밀도함수(PDF)가 생성된다. 역변환 샘플링(inverse transform sampling)을 사용하여 이 분포에서 $N_f$개의 위치들의 집합을 샘플링하고, 첫 번째와 두 번째 샘플 집합의 합집합에서 fine 네트워크를 평가하고, 모든 $N_c + N_f$개의 샘플을 사용하여 광선의 최종 렌더링된 색상 \(\hat{C}_f (\mathbf{r})\)을 계산한다.

이 절차에서는 보이는 콘텐츠가 포함될 것으로 예상되는 영역에 더 많은 샘플을 할당한다. 이는 중요도 샘플링과 비슷한 목표를 가지지만, 각 샘플을 전체 적분의 독립적인 확률적 추정으로 처리하는 대신 샘플링된 값을 전체 적분 영역의 nonuniform discretization으로 사용한다.

3. Implementation details

각 장면에 대해 별도의 NeRF 표현 신경망을 최적화한다. 이를 위해서는 장면의 캡처된 RGB 이미지, 해당 카메라 포즈, intrinsic parameter, 장면 경계로 구성된 데이터셋만 필요하다. 각 최적화 iteration에서 데이터셋의 모든 픽셀 집합에서 카메라 광선 batch를 무작위로 샘플링한 다음 계층적 샘플링을 따라 coarse 네트워크의 $N_c$개의 샘플과 fine 네트워크의 $N_c + N_f$개의 샘플을 쿼리한다. 그런 다음 볼륨 렌더링 절차를 사용하여 두 샘플 집합 모두에서 각 광선의 색상을 렌더링한다. Loss는 단순히 coarse 렌더링과 fine 렌더링 모두에 대해 렌더링된 픽셀 색상과 실제 픽셀 색상 간의 총 제곱 오차이다.

\[\begin{equation} \mathcal{L} = \sum_{\mathbf{r} \in \mathcal{R}} [ \| \hat{C}_c (\mathbf{r}) - C (\mathbf{r}) \|_2^2 + \| \hat{C}_f (\mathbf{r}) - C (\mathbf{r}) \|_2^2] \end{equation}\]

여기서 $\mathcal{R}$은 각 batch의 광선 집합이고, $C(\mathbf{r})$는 실제 RGB 색상, \(\hat{C}_c (\mathbf{r})\)는 coarse 네트워크의 예측 RGB 색상, \(\hat{C}_f (\mathbf{r})\)는 fine 네트워크의 예측 RGB 색상이다. 최종 렌더링이 \(\hat{C}_f (\mathbf{r})\)에서 나오지만 \(\hat{C}_c (\mathbf{r})\)의 loss도 최소화하여 coarse 네트워크의 가중치 분포를 사용하여 fine 네트워크에 샘플을 할당할 수 있다.

Experiments

• 데이터셋: 자체 제작
  • 합성 렌더링: Diffuse Synthetic 360◦, Realistic Synthetic 360◦
  • 현실 이미지: Real Forward-Facing
• 구현 디테일
  • batch size: 4096
  • $N_c$ = 64, $N_f$ = 128
  • optimizer: Adam ($\beta_1$ = 0.9, $\beta_2$ = 0.999)
  • learning rate: $5 \times 10^{-4}$
  • iteration: 한 장면당 10~30만 (NVIDIA V100 GPU 1개로 1~2일 소요)

1. Comparisons

다음은 각 데이터셋에 대하여 이전 연구들과 정량적으로 비교한 표이다.

다음은 합성 데이터셋에서의 새로운 뷰 합성 결과를 비교한 것이다.

다음은 현실 이미지 데이터셋에서의 새로운 뷰 합성 결과를 비교한 것이다.

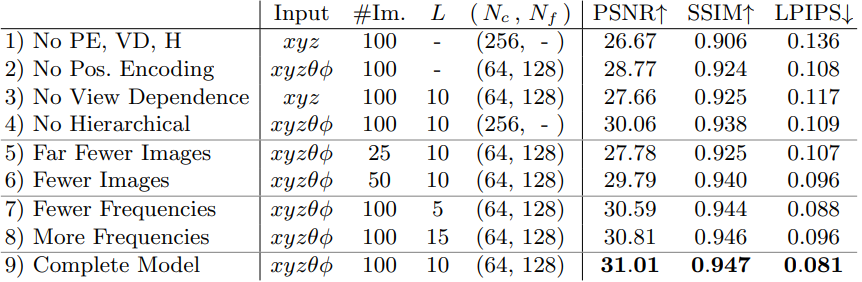
2. Ablation studies

다음은 ablation study 결과이다. PE는 위치 인코딩, VD는 뷰 의존성, H는 계층적 샘플링이다.