[논문리뷰] Neighborhood Attention Transformer (NAT)
CVPR 2023. [Paper] [Github]
Ali Hassani, Steven Walton, Jiachen Li, Shen Li, Humphrey Shi
SHI Labs | Picsart AI Research (PAIR) | Meta AI
14 Apr 2022

Introduction
CNN은 수년간 다양한 애플리케이션에서 컴퓨터 비전 모델을 위한 사실상의 표준 아키텍처였다. AlexNet은 ImageNet에서 유용성을 보여주었고 다른 많은 사람들도 VGG, ResNet, EfficientNet과 같은 아키텍처를 사용했다. 반면 Transformer는 원래 자연어 처리를 위한 attention 기반 모델로 제안되어 언어의 순차적 구조를 이용하려고 시도했다. Transformer는 BERT와 GPT가 구축된 기반이었으며 계속해서 NLP의 SOTA 아키텍처이다.
Vision Transformer (ViT)는 주로 대규모 학습을 위해 이미지 패치의 embedded space에서 작동하는 Transformer 인코더만 사용하는 이미지 classifier로 제안되었다. 그 뒤를 이어 데이터 효율성을 높이기 위한 여러 다른 방법이 뒤따랐고 결국 이러한 Transformer와 같은 모델을 ImageNet-1K 분류의 SOTA로 만들었다 (JFT-300M과 같은 대규모 데이터셋에 대한 사전 학습 없이).
이러한 고성능 Transformer와 같은 방법은 모두 원래 Transformer의 기본 빌딩 블록인 Self Attention (SA)를 기반으로 한다. SA는 임베딩 차원 (linear projection 제외)에 대하여 선형 복잡도를 갖지만 토큰 수에 대하여 2차 복잡도를 갖는다. 비전에서 토큰의 수는 일반적으로 이미지 해상도와 선형 상관 관계에 있다. 결과적으로 이미지 해상도가 높을수록 ViT와 같이 SA를 엄격하게 사용하는 모델에서 복잡도와 메모리 사용량이 2차적으로 증가한다. 2차 복잡도로 인해 ViT는 일반적으로 이미지 해상도가 classification보다 훨씬 더 큰 object detection과 segmentation과 같은 다운스트림 비전 task에 쉽게 적용할 수 없다. 또 다른 문제는 convolution이 locality나 2차원 공간 구조와 같은 inductive bias들로부터 이익을 얻는 반면, 내적 self attention은 정의상 글로벌한 1차원 연산이라는 것이다. 즉, 이러한 inductive bias 중 일부는 많은 양의 데이터나 고급 학습 기술과 augmentation을 통해 학습되어야 한다.
따라서 이러한 문제를 완화하기 위해 local attention 모듈이 제안되었다. Stand-Alone Self-Attention (SASA)는 각 픽셀이 주위의 window에 attend하는 local window 기반 attention의 초기 응용 중 하나였다. 명시적인 sliding window 패턴은 동일한 convolution과 동일하며 패딩이 0이고 간단한 2차원 rastar scan을 사용하므로 translational equivariance이 유지된다. SASA는 ResNet에서 convolution을 대체하는 것을 목표로 했으며 baseline에 비해 눈에 띄게 개선되었다. 그러나 SASA는 convolution과 유사한 효율적인 구현이 없기 때문에 속도 면에서 제한적이다.
반면에 Swin은 local self attention을 기반으로 한 최초의 계층적 ViT 중 하나였다. Swin의 디자인과 shifted-window self-attention은 계산적으로 실현 가능하게 만들었기 때문에 다운스트림 task에 쉽게 적용할 수 있게 해 주었고 추가 바이어스를 주입하여 성능을 향상시켰다. 그러나 Swin의 localized attention은 먼저 겹치지 않는 windwow에 self-attention을 적용한 다음 window를 이동시킨다. HaloNet은 픽셀 단위가 아니라 한 번에 픽셀 블록에 대한 self-attention을 localize하는 haloing 메커니즘을 사용했다.
본 논문에서는 명시적인 sliding window attention 메커니즘을 재검토하고 Neighborhood Attention (NA)를 제안한다. NA는 SA를 각 픽셀의 nearest neighbor로 localize하며, 이는 반드시 픽셀 주변의 고정된 window일 필요는 없다. 이러한 정의 변경으로 모든 픽셀이 동일한 attention 범위를 유지할 수 있으며, 이는 모서리 픽셀의 attention 범위가 줄어드는 zero padding 방법 (SASA)과 다르다. 또한 NA는 neighborhood 크기가 커짐에 따라 SA에 접근하며 최대 neighborhood에서 SA와 동일하며, translational equivariance을 유지하는 추가 이점이 있다. 저자들은 비전 task에서 경쟁력 있는 결과를 달성하는 Neighborhood Attention Transformer (NAT)를 구축하였다.
Method
1. Neighborhood Attention
Swin의 WSA (window self attention)는 2차 attention 비용을 줄이기 위해 self attention을 제한하는 가장 빠른 기존 방법 중 하나이다. 단순히 입력을 분할하고 각 분할에 개별적으로 self attention을 적용한다. WSA는 window 밖의 상호 작용을 허용하기 위해 분할선을 이동하는 SWSA (shifted WSA)와 쌍을 이루어야 한다. 이것은 receptive field를 확장하는 데 중요하다. 그럼에도 불구하고 self attention을 로컬로 제한하는 가장 직접적인 방법은 각 픽셀이 인접한 픽셀에 attend하도록 하는 것이다. 그 결과 대부분의 픽셀 주변에 동적으로 shifted window가 있어 receptive field가 확장되므로 수동으로 이동시킬 필요가 없다. 또한 convolution과 유사하게 이러한 제한된 self attention의 동적 형태는 translational equivariance를 보존할 수 있다.
여기서 영감을 받아 Neighborhood Attention (NA)를 도입한다. 행이 $d$차원 토큰 벡터인 입력 행렬 $X \in \mathbb{R}^{n \times d}$, $X$의 linear projection $Q$, $K$, $V$, 상대 위치 바이어스 $B(i, j)$가 주어지면, neighborhood 크기 $k$와 $i$번째 입력에 대하여 $i$번째 입력의 query projection과 $k$개의 nearest neighboring key projection의 내적으로 attention 가중치 $A_i^k$를 정의한다.
\[\begin{equation} A_i^k = \begin{bmatrix} Q_i K_{\rho_1 (i)}^\top + B_{(i, \rho_1 (i))} \\ Q_i K_{\rho_2 (i)}^\top + B_{(i, \rho_2 (i))} \\ \vdots \\ Q_i K_{\rho_k (i)}^\top + B_{(i, \rho_k (i))} \end{bmatrix} \end{equation}\]여기서 $\rho_j (i)$는 $i$의 $j$번째 nearest neighbor을 나타낸다. 그런 다음 neighboring value $V_i^k$를 행이 $i$번째 입력의 $k$번째 nearest neighboring value projection인 행렬로 정의한다.
\[\begin{equation} V_i^k = [V_{\rho_1 (i)}^\top \; V_{\rho_2 (i)}^\top \; \cdot \; V_{\rho_k (i)}^\top ]^\top \end{equation}\]Neighborhood 크기가 $k$인 $i$번째 토큰에 대한 Neighborhood Attention은 다음과 같이 정의된다.
\[\begin{equation} \textrm{NA}_k (i) = \textrm{softmax} \bigg(\frac{A_i^k}{\sqrt{d}}\bigg) V_i^k \end{equation}\]여기서 $\sqrt{d}$는 스케일링 파라미터이다. 이 연산은 feature map의 모든 픽셀에 대해 반복된다. 이 연산은 아래 그림에 나와 있다.
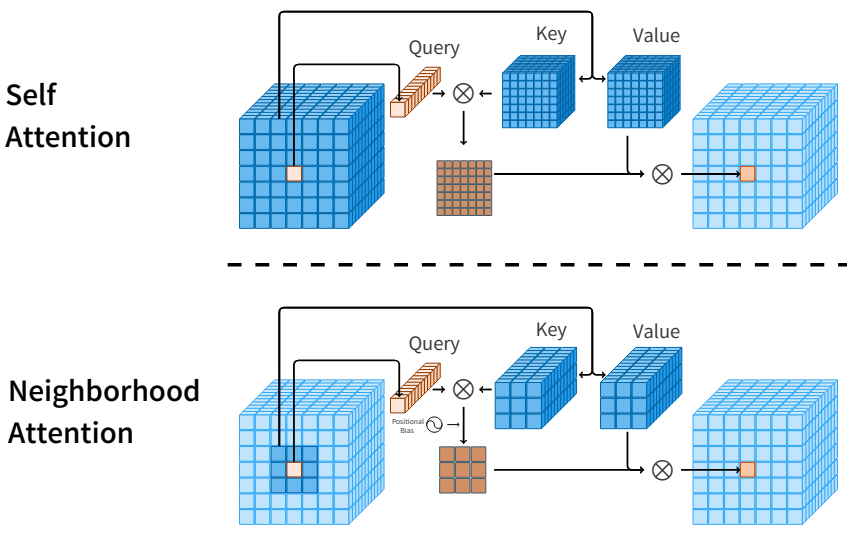
이 정의에서 $k$가 커짐에 따라 $A_i^k$는 self attention 가중치에 접근하고 $V_i^k$는 $V_i$ 자체에 접근하므로 Neighborhood Attention이 self attention에 접근한다는 것을 쉽게 알 수 있다. 이것이 NA와 SASA의 주요 차이점이다. SASA는 가장자리를 처리하기 위해 입력 주변에 패딩을 사용하여 주변 window에 attend한다. 입력 주변의 zero padding으로 인해 SASA는 self attention에 접근할 수 없지만, window 크기가 커짐에 따라 NA가 self attention에 접근하는 것은 이러한 차이 덕분이다.
2. Tiled NA and $\mathcal{N}$ATTEN
Pixel-wise 방식으로 self attention을 제한하는 것은 주로 낮은 수준의 재구현이 필요한 비용이 많이 드는 연산으로 간주되었기 때문에 과거에는 잘 탐색되지 않았다. Self attention 자체가 가속기에서 쉽게 병렬화할 수 있는 연산인 행렬 곱셈으로 분류되고, 계산 소프트웨어의 수많은 효율적인 알고리즘이 있기 때문이다. 또한 PyTorch와 같은 대부분의 딥러닝 플랫폼은 이러한 소프트웨어와 추가 패키지 (ex. cuDNN) 위에 작성된다. 백엔드가 하드웨어, 소프트웨어, 사용 사례에 따라 실행할 알고리즘을 결정하는 동안 행렬 곱셈 또는 convolution과 같은 연산의 추상화를 사용할 수 있으므로 매우 유용하다. 또한 일반적으로 자동 기울기 계산을 처리하므로 심층 신경망을 매우 간단하게 설계하고 학습할 수 있다.
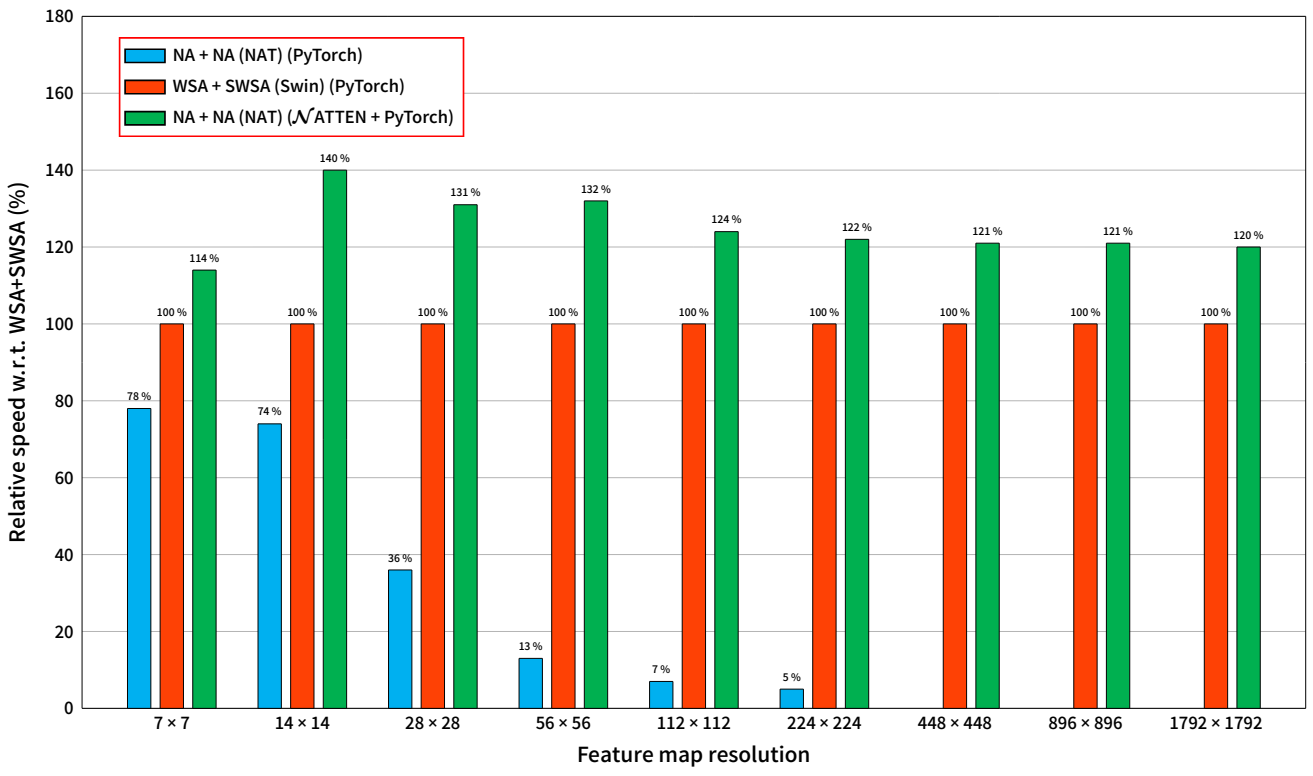
NA의 pixel-wise 구조와 NA에서 neighborhood 정의의 참신함 때문에 이러한 플랫폼에서 NA를 구현하는 유일한 방법은 여러 개의 비효율적인 연산들을 쌓아 neighborhood을 추출하고 중간 텐서로 저장한 다음 attention을 계산하는 것이다. 이로 인해 메모리 사용량이 기하급수적으로 증가하면서 연산 속도가 크게 느려진다. 이러한 문제를 해결하기 위해 저자들은 효율적인 CPU와 CUDA 커널 세트를 개발하고 이를 Python 패키지인 $\mathcal{N}$ATTEN (Neighborhood Attention Extension)으로 패키징했다 (링크). $\mathcal{N}$ATTEN에는 반정밀도 지원, 1D 및 2D 데이터 지원, PyTorch와의 autograd 호환 통합이 포함된다. 즉, 사용자는 NA를 PyTorch 모듈로 가져와서 기존 파이프라인에 통합할 수 있다. 또한 SASA는 NA의 특수한 경우이므로 기본 커널을 변경하지 않고 단순히 입력을 0으로 패딩하여 이 패키지로 쉽게 구현할 수 있다. 또한 겹치지 않는 query 타일을 공유 메모리에 로드하여 글로벌 메모리 읽기를 최소화하여 NA 가중치를 계산하는 tiled NA algorithm도 포함되어 있다. 순진한 구현과 비교할 때 tiled NA는 대기 시간을 최대 10배까지 줄일 수 있으며 NA 기반 모델이 유사한 Swin 모델보다 최대 40% 더 빠르게 실행할 수 있다 (아래 그래프 참조).
3. Neighborhood Attention Transformer
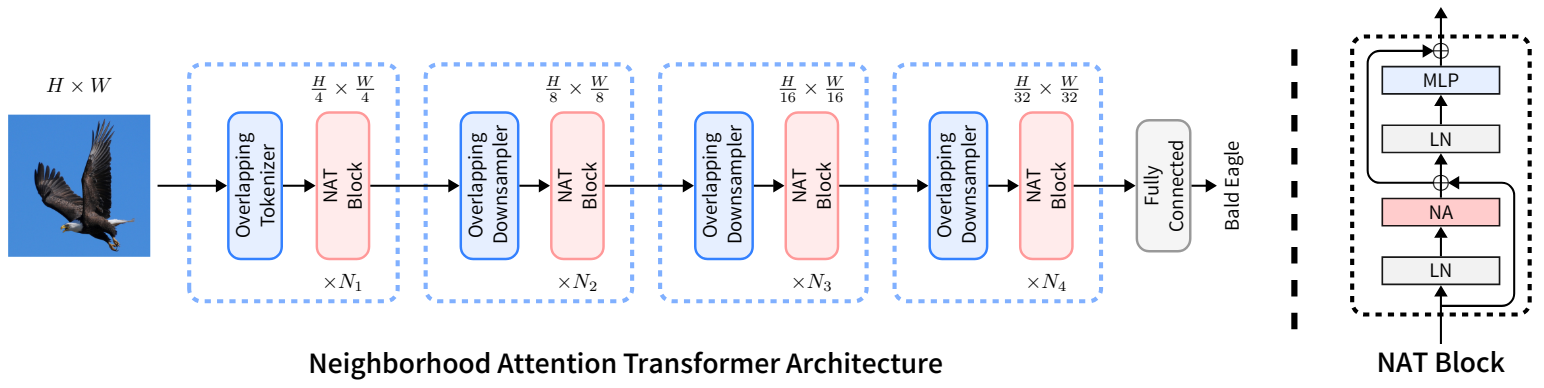
NAT는 2$\times$2 stride가 있는 2개의 연속 3$\times$3 convolution을 사용하여 입력을 임베딩하므로 공간 크기가 입력 크기의 1/4이 된다. 이것은 4$\times$4 패치가 있는 패치 및 임베딩 레이어를 사용하는 것과 유사하지만 유용한 inductive bias를 도입하기 위해 non-overlapping convolution 대신 overlapping convolution을 사용한다. 반면 overlapping convolution을 사용하면 비용이 증가하고 두 개의 convolution은 더 많은 파라미터를 발생시킨다. 그러나 모델을 재구성하여 더 나은 절충안을 도출한다. NAT는 4개 레벨로 구성되며 각 레벨 뒤에는 다운샘플러가 있다 (마지막 제외). 다운샘플러는 공간 크기를 절반으로 줄이면서 채널 수를 두 배로 늘린다. Swin이 사용하는 2$\times$2 non-overlapping convolution 대신 2$\times$2 stride가 있는 3$\times$3 convolution을 사용한다. Tokenizer가 4배로 다운샘플링하기 때문에 모델은 $\frac{h}{4} \times \frac{w}{4}$, $\frac{h}{8} \times \frac{w}{8}$, $\frac{h}{16} \times \frac{w}{16}$, $\frac{h}{32} \times \frac{w}{32}$ 크기의 feature map을 생성한다. 또한 더 큰 변형에서 안정성을 위해 LayerScale을 사용한다. 전체 네트워크 아키텍처에 대한 그림은 아래와 같다.
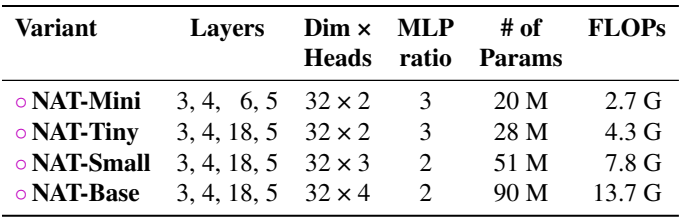
아래 표에는 다양한 NAT 변형에 대한 요약이 나와 있다.
4. Complexity Analysis
다양한 attention 패턴과 convolution에서 계산 비용과 메모리 사용량은 아래 표와 같다.

Experiments
1. Classification
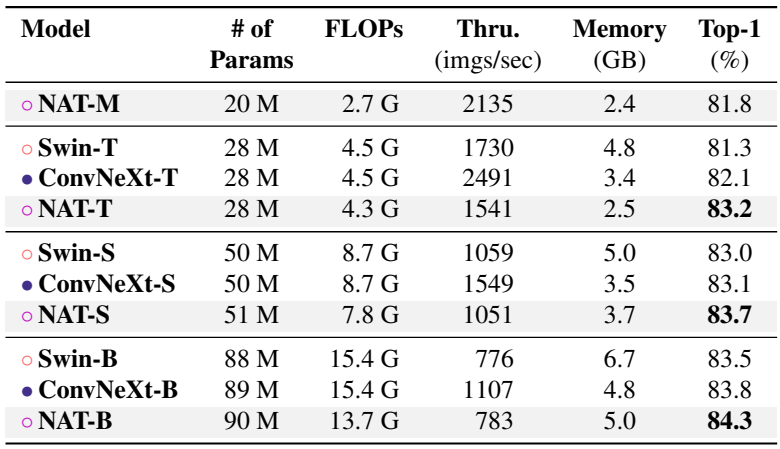
다음은 ImageNet-1K classification 성능이다.
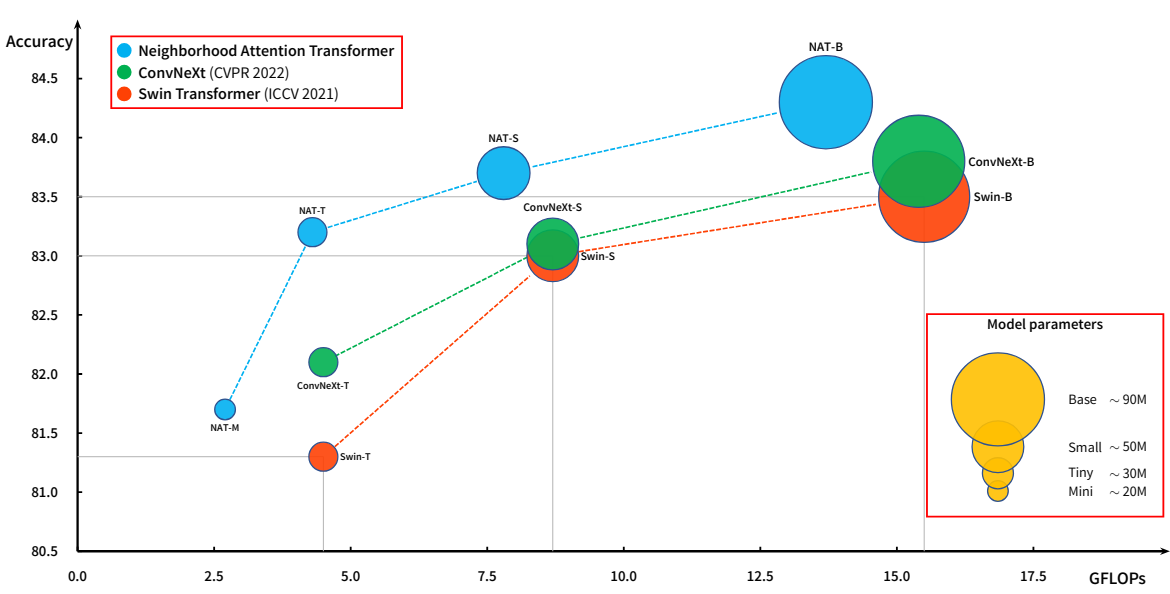
다음은 계산 비용에 따른 ImageNet-1K classification 성능을 나타낸 표이다. 원의 크기는 파라미터 수를 나타낸다.
2. Object Detection and Instance Segmentation
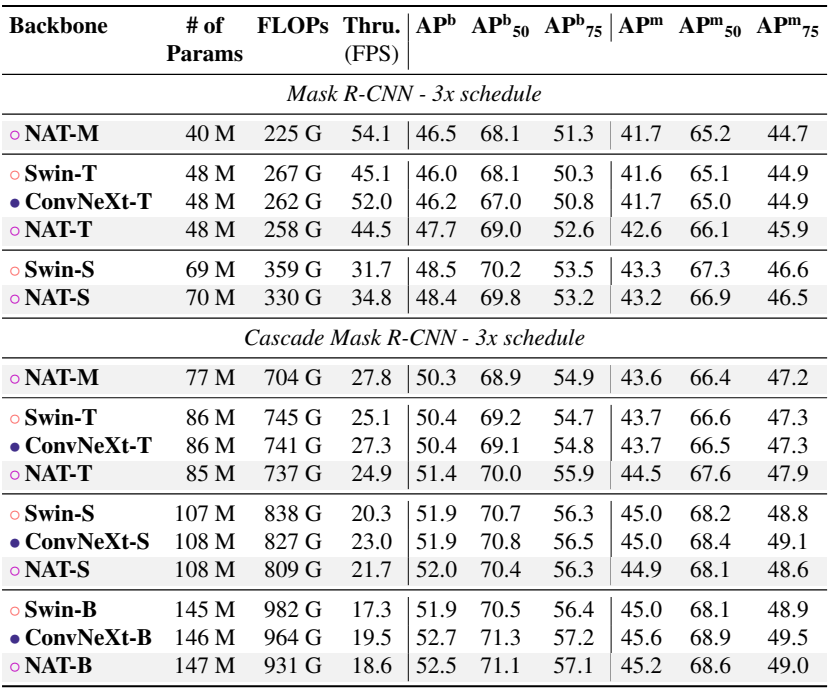
다음은 COCO object detection과 instance segmentation 성능이다.
3. Semantic Segmentation
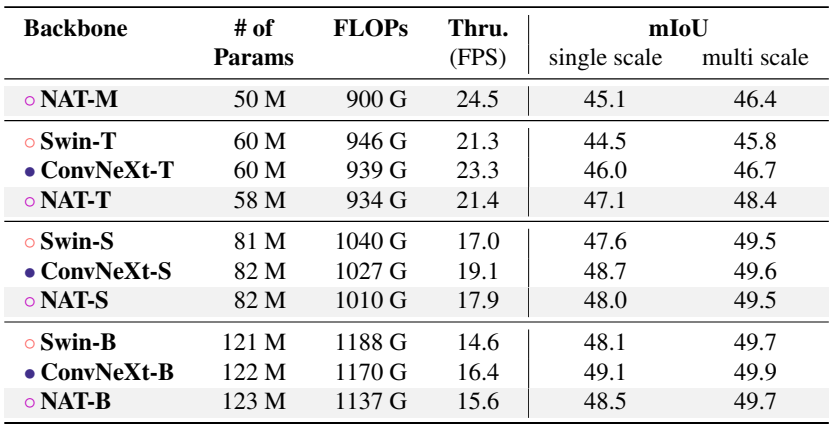
다음은 ADE20K semantic segmentation 성능이다.
4. Ablation Study
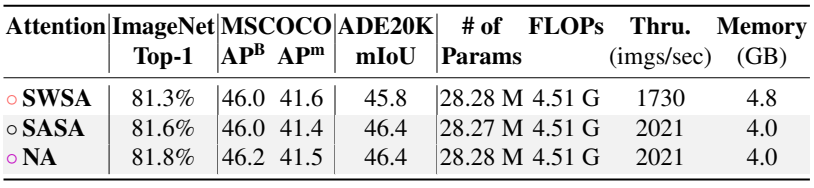
다음은 다양한 attention 메커니즘에 대한 성능을 비교한 표이다.
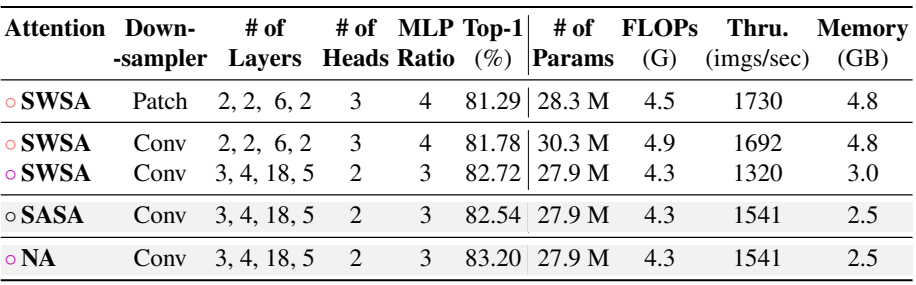
다음은 NAT에 대한 ablation study 결과이다.
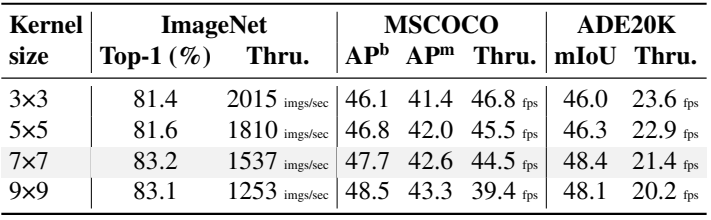
다음은 다양한 커널 크기에 대한 NAT-Tiny의 성능을 비교한 표이다.