[논문리뷰] Multiscale Vision Transformers (MViT)
arXiv 2021. [Paper] [Github]
Haoqi Fan, Bo Xiong, Karttikeya Mangalam, Yanghao Li, Zhicheng Yan, Jitendra Malik, Christoph Feichtenhofer
Facebook AI Research | UC Berkeley
22 Apr 2021
Introduction
컴퓨터 비전 커뮤니티는 “피라미드” 전략이라고도 하는 멀티스케일 처리를 개발했다. 두 가지 동기가 있었다.
- 낮은 해상도에서 연산하여 컴퓨팅 요구 사항을 줄일 수 있다.
- 낮은 해상도에서 더 나은 “컨텍스트” 감각을 제공하여 더 높은 해상도에서 처리를 가이드할 수 있다. (이는 오늘날 신경망의 “깊이”의 이점을 보여준다.)
Transformer 아키텍처를 사용하면 집합에 걸쳐 정의된 임의 함수를 학습할 수 있으며 언어 이해 및 기계 번역과 같은 시퀀스 task에서 확장성 있게 성공했다. 기본적으로 transformer는 두 가지 기본 연산이 있는 블록을 사용한다. 첫째는 요소 간 관계를 모델링하기 위한 attention 연산이고, 둘째는 요소 내의 관계를 모델링하는 MLP이다. 이러한 연산들을 정규화 및 residual connection과 얽히게 하면 transformer가 다양한 task로 일반화될 수 있다.
최근에는 이미지 분류와 같은 주요 컴퓨터 비전 task에 transformer가 적용되었다. ViT는 다양한 데이터 및 컴퓨팅 방식에 걸쳐 convolutional model의 성능에 접근하였다. ViT는 2D convolution 정신으로 입력을 패치화(patchify)하는 첫 번째 레이어와 transformer 블록 스택만 가짐으로써 inductive bias를 거의 사용하지 않고 transformer 아키텍처의 성능을 보여주는 것을 목표로 하였다.
본 논문의 목표는 멀티스케일 feature 계층의 아이디어를 transformer 모델과 연결하는 것이다. 저자들은 해상도 및 채널 스케일링의 기본 비전 원리가 다양한 비전 인식 task에 걸쳐 transformer 모델에 도움이 될 수 있다고 가정하였다.
본 논문은 이미지, 동영상 등의 시각적 데이터를 모델링하기 위한 transformer 아키텍처인 Multiscale Vision Transformers (MViT)를 소개한다. 네트워크 전체에서 일정한 채널 용량과 해상도를 유지하는 기존 transformer과 달리 멀티스케일 transformer는 여러 채널-해상도 ‘scale’ stage가 있다. 이미지 해상도와 작은 채널 차원에서 시작하여 stage는 공간 해상도를 줄이면서 채널 용량을 계층적으로 확장한다. 이는 transformer 네트워크 내부에 feature activation의 멀티스케일 피라미드를 생성하여 transformer의 원리를 멀티스케일 feature 계층과 효과적으로 연결한다.
이 개념적 아이디어는 ViT 모델에 효과적인 디자인 이점을 제공한다. 아키텍처의 초기 레이어는 가벼운 채널 용량 덕분에 높은 공간 해상도에서 작동하여 단순한 낮은 수준의 시각적 정보를 모델링할 수 있다. 결과적으로 더 깊은 레이어는 시각적 의미를 모델링하기 위해 공간적으로 대략적이지만 복잡한 상위 수준 feature에 효과적으로 집중할 수 있다. 멀티스케일 transformer의 근본적인 장점은 시각적 신호의 밀도가 매우 높은 특성에서 발생하며, 이는 동영상에 캡처된 시공간 시각적 신호에서 더욱 두드러지는 현상이다.
본 논문의 디자인의 주목할만한 이점은 동영상 멀티스케일 모델에 강력한 암시적 시간적 편향이 존재한다는 것이다. 저자들은 동영상으로 학습된 ViT 모델이 셔플된 프레임이 있는 동영상에서 테스트할 때 성능 저하가 발생하지 않음을 보여주었다. 이는 이러한 모델이 시간 정보를 효과적으로 사용하지 않고 대신 외형에 크게 의존하고 있음을 나타낸다. 대조적으로, 셔플된 프레임에서 MViT 모델을 테스트할 때에는 시간 정보의 강력한 사용을 나타내는 상당한 정확도 저하가 관찰되었다.
본 논문의 초점은 동영상 인식이며, 동영상 task (Kinetics, Charades, SSv2, AVA)을 위한 MViT를 설계하고 평가한다. MViT는 외부 사전 학습 데이터 없이 동영상 transformer에 비해 상당한 성능 향상을 제공한다.
Multiscale Vision Transformer (MViT)
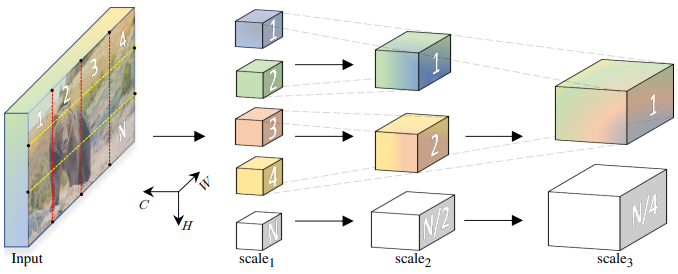
일반적인 Multiscale Transformer 아키텍처는 stage라는 핵심 개념을 기반으로 구축되었다. 각 stage는 특정 시공간 해상도와 채널 크기를 갖는 여러 transformer 블록으로 구성된다. Multiscale Transformer의 주요 아이디어는 네트워크의 입력에서 출력까지 해상도를 pooling하면서 채널 용량을 점진적으로 확장하는 것이다.
1. Multi Head Pooling Attention
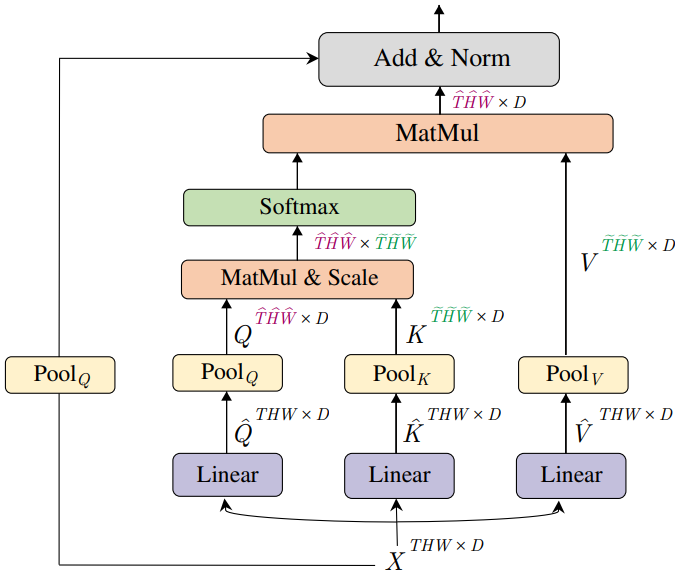
먼저 Multiscale Transformer가 점진적으로 변화하는 시공간 해상도에서 작동할 수 있도록 transformer 블록에서 유연한 해상도 모델링을 가능하게 하는 self-attention 연산자인 Multi Head Pooling Attention (MHPA)를 도입한다. 채널 차원과 시공간 해상도가 고정된 원래 Multi Head Attention (MHA) 연산자와 달리 MHPA는 latent 텐서 시퀀스를 pooling하여 attend된 입력의 시퀀스 길이(해상도)를 줄인다. 위 그림은 그 개념을 보여준다.
구체적으로, 시퀀스 길이가 $L$인 $D$차원 입력 텐서 $X \in \mathbb{R}^{L \times D}$를 고려하자. MHA를 따라 MHPA는 선형 연산을 통해 입력 $X$를 중간 query 텐서 $\hat{Q} \in \mathbb{R}^{L \times D}$, key 텐서 $\hat{K} \in \mathbb{R}^{L \times D}$, value 텐서 $\hat{V} \in \mathbb{R}^{L \times D}$에 $D \times D$ 차원 가중치 $W_Q$, $W_K$, $W_V$를 사용하여 project한다.
\[\begin{equation} \hat{Q} = X W_Q, \quad \hat{K} = XW_K, \quad \hat{V} = XW_V \end{equation}\]이 중간 텐서들은 pooling 연산자 $\mathcal{P}$를 사용하여 시퀀스 길이로 pooling된다.
Pooling Operator
입력에 attend하기 전에 중간 텐서 $\hat{Q}$, $\hat{K}$, $\hat{V}$는 MHPA를 확장하여 Multiscale Transformer 아키텍처의 초석인 pooling 연산자 $\mathcal{P}(\cdot; \Theta)$로 pooling된다.
연산자 $\mathcal{P}(\cdot; \Theta)$는 각 차원에 따라 입력 텐서에 대해 pooling 커널 계산을 수행한다. $\Theta$를 $\Theta := (k, s, p)$로 풀면 연산자는 $k_T \times k_H \times k_W$ 차원의 pooling 커널 $k$, $s_T \times s_H \times s_W$ 차원의 stride $s$, $p_T \times p_H \times p_W$ 차원의 패딩 $p$를 사용하여 입력 텐서 $L = T \times H \times W$를 $\tilde{L}$로 줄인다.
\[\begin{equation} \tilde{L} = \bigg\lfloor \frac{L + 2p - k}{s} \bigg\rfloor + 1 \end{equation}\]pooling된 텐서는 다시 평탄화되어 시퀀스 길이가 감소된 $\mathcal{P} (Y; \Theta) \in \mathbb{R}^{\tilde{L} \times D}$의 출력을 생성한다.
기본적으로 pooling attention 연산자에서 모양 보존 패딩 $p$와 중첩 커널 $k$를 사용하므로 출력 텐서 $\mathcal{P} (Y; \Theta)$의 시퀀스 길이인 $\tilde{L}$은 $s_T s_H s_W$배만큼 감소한다.
Pooling Attention
Pooling 연산자 $\mathcal{P} (\cdot; \Theta)$는 선택된 pooling 커널 $k$, stride $s$, 패딩 $p$와 독립적으로 모든 중간 텐서 $\hat{Q}$, $\hat{K}$, $\hat{V}$에 적용된다. 그러면 시퀀스 길이가 감소된 pre-attention 벡터 $Q = \mathcal{P} (\hat{Q}; \Theta_Q)$, $K = \mathcal{P} (\hat{K}; \Theta_K)$, $V = \mathcal{P} (\hat{V}; \Theta_V)$가 생성된다. 이러한 단축된 벡터에 대해 attention이 계산된다.
\[\begin{equation} \textrm{Attention}(Q, K, V) = \textrm{Softmax}(\frac{QK^\top}{\sqrt{D}}) V \end{equation}\]당연히 이 연산은 pooling 연산자에 대한 제약 조건 $s_K \equiv s_V$이 도입된다. 요약하면, pooling attention은 다음과 같이 계산된다.
\[\begin{equation} \textrm{PA} (\cdot) = \textrm{Softmax}(\frac{\mathcal{P}(Q; \Theta_Q) \mathcal{P} (K; \Theta_K)^\top}{\sqrt{d}}) \mathcal{P} (V; \Theta_V) \end{equation}\]여기서 $\sqrt{d}$는 내적한 행렬을 행 단위로 정규화한다. 따라서 pooling attention 연산의 출력은 $\mathcal{P}(\cdot)$에서 query 벡터 $Q$가 단축된 후 $s_T^Q s_H^Q s_W^Q$의 stride factor만큼 감소된 시퀀스 길이를 갖는다.
Multiple heads
각 head가 $D$ 차원 입력 텐서 $X$의 $D/h$ 채널의 겹치지 않는 부분집합에 대해 pooling attention을 수행하는 $h$개의 head를 고려하여 계산을 병렬화할 수 있다.
Computational Analysis
Attention 계산은 시퀀스 길이에 따라 2차적으로 확장되므로 key, query, value 텐서를 풀링하면 Multiscale Transformer 모델의 기본 계산 및 메모리 요구 사항에 극적인 이점이 있다. 시퀀스 길이가 각각 $f_Q$, $f_K$, $f_V$배만큼 감소한다고 하면, 모든 \(j \in \{Q, K, V\}\)에 대하여 $f_j = s_T^j \cdot s_H^j \cdot s_W^j$이다.
$\mathcal{P}(; \Theta)$에 대한 입력 텐서가 $D \times T \times H \times W$ 차원을 갖는 것을 고려하면 MHPA의 런타임 복잡도는 head당 $O(THWD/h(D + THW/f_Qf_K))$이고 메모리는 복잡도는 $O(THWh(D/h + THW/f_Qf_K))$이다.
채널 수 $D$와 시퀀스 길이 항 $THW/f_Qf_K$ 사이의 이러한 trade-off를 이용하여 저자들은 head 수와 레이어 너비와 같은 아키텍처 파라미터 선택을 결정하였다.
2. Multiscale Transformer Networks
본 논문은 Multi Head Pooling Attention을 기반으로 MHPA와 MLP 레이어만 사용하는 시각적 표현 학습을 위한 Multiscale Transformer 모델을 도입하였다.
Preliminaries: Vision Transformer (ViT)

ViT 아키텍처는 해상도 $T \times H \times W$의 입력 동영상을 각각 $1 \times 16 \times 16$ 크기의 겹치지 않는 패치로 분할하는 것으로 시작한다 (여기서 $T$는 프레임 수 $H$는 높이, $W$는 너비). 그런 다음 flatten된 이미지 패치에 linear layer를 point-wise로 적용하여 이를 transformer의 latent 차원 $D$에 project한다. 이는 동일한 커널 크기와 $1 \times 16 \times 16$의 stride를 갖는 convolution과 동일하며 위 표의 모델 정의에서 patch1 stage로 표시된다.
다음으로, 위치 정보를 인코딩하고 순열 불변성을 깨기 위해 차원이 $D$이고 길이가 $L$인 project된 시퀀스의 각 요소에 위치 임베딩 $E \in \mathbb{R}^{L \times D}$가 추가된다. 학습 가능한 클래스 임베딩이 project된 이미지 패치에 추가된다.
길이가 $L + 1$인 결과 시퀀스는 $N$개의 transformer 블록 스택에 의해 순차적으로 처리되며, 각 블록은 attention (MHA), MLP, layer normalization (LN) 연산을 수행한다. $X$를 블록의 입력으로 간주하면 하나의 transformer 블록의 출력인 $\textrm{Block}(X)$는 다음과 같이 계산된다.
\[\begin{aligned} X_1 &= \textrm{MHA} (\textrm{LN} (X)) + X \\ \textrm{Block} (X) &= \textrm{MLP} (\textrm{LN} (X_1)) + X_1 \end{aligned}\]$N$개의 연속되는 블록 이후의 결과 시퀀스는 layer-normalize되고 클래스 임베딩이 추출되어 linear layer를 통과하여 원하는 출력(ex. 클래스)을 예측한다. 기본적으로 MLP의 hidden 차원은 $4D$이다.
본 논문의 맥락에서 ViT가 모든 블록에 걸쳐 일정한 채널 용량과 공간 해상도를 유지한다는 점은 주목할 만하다.
Multiscale Vision Transformers (MViT)

본 논문의 핵심 개념은 채널 해상도 (즉, 차원)를 점진적으로 늘리는 동시에 네트워크 전체에서 시공간 해상도 (즉, 시퀀스 길이)를 줄이는 것이다. 설계상 MViT 아키텍처는 초기 레이어에서 세밀한 시공간 해상도와 대략적인 채널 해상도를 가지며, 나중 레이어에서는 대략적인 시공간 해상도와 세밀한 채널 해상도로 업/다운샘플링된다. MViT는 위 표에 나와 있다.
Scale stages
Scale stage는 채널 및 시공간 차원 $D \times T \times H \times W$ 전체에서 동일한 해상도로 동일한 스케일에서 작동하는 $N$개의 transformer 블록 집합으로 정의된다. 입력 (위 표의 cube1)에서 패치(또는 시간 범위가 있는 경우 큐브)를 더 작은 채널 차원 (ex. 일반적인 ViT 모델보다 8배 더 작음)으로 project하지만 긴 시퀀스 (ex. 일반적인 ViT 모델보다 밀도가 16배 더 높다)를 가진다.
Stage 전환 시 처리된 시퀀스의 채널 차원은 업샘플링되는 반면 시퀀스의 길이는 다운샘플링된다. 이는 기본 시각적 데이터의 시공간 해상도를 효과적으로 줄이는 동시에 네트워크가 더 복잡한 feature의 처리된 정보를 받아들일 수 있도록 한다.
Channel expansion
한 stage에서 다음 stage로 전환할 때 이전 stage의 최종 MLP layer의 출력을 증가시켜 채널 차원을 확장한다. 구체적으로 시공간 해상도를 4배로 다운샘플링하면 채널 차원이 2배 증가한다. 이는 stage 전체에서 계산 복잡도를 대략적으로 유지하며 ConvNet 디자인 원칙과 유사하다.
Query pooling
Pooling attention 연산은 key와 value 벡터의 길이뿐만 아니라 query의 길이와 그에 따른 출력 시퀀스에도 유연성을 제공한다. Query 벡터 $\mathcal{P}(Q; k; p; s)$를 커널 $s \equiv (s_T^Q, s_H^Q, s_W^Q)$로 pooling하면 $s_T^Q \cdot s_H^Q \cdot s_W^Q$만큼 시퀀스가 줄어든다. 저자들의 의도는 stage 시작 부분에서 해상도를 낮추고 stage 전체에서 이 해상도를 유지하는 것이므로 각 stage의 첫 번째 pooling attention 연산자만 감소하지 않는 query stride $s^Q > 1$에서 작동하고 다른 모든 연산자는 $s^Q \equiv (1, 1, 1)$로 제한된다.
Key-Value pooling
Query 풀링과 달리 key $K$와 value $V$ 텐서의 시퀀스 길이를 변경해도 출력 시퀀스 길이가 변경되지 않으므로 시공간 해상도도 변경되지 않는다. 그러나 이는 pooling attention 연산자의 전반적인 계산 요구량에서 중요한 역할을 한다.
저자들은 $K$, $V$, $Q$ pooling의 사용을 분리하였다. $Q$ pooling은 각 stage의 첫 번째 레이어에서 사용되고 $K$, $V$ pooling은 다른 모든 레이어에서 사용된다. Attention 가중치 계산을 위해서는 key 텐서와 value 텐서의 시퀀스 길이가 동일해야 하므로 key 텐서와 value 텐서에 사용되는 pooling stride가 동일해야 한다. 기본 설정에서는 모든 pooling 매개변수 $(k; p; s)$가 한 stage 내에서 동일하도록 (즉, $\Theta_K = \Theta_V$) 제한하지만 stage 전체의 스케일에 따라 $s$는 적응적으로 달라진다.
Skip connections
Residual block 내에서 채널 차원과 시퀀스 길이가 변경되므로 두 끝 사이의 차원 불일치에 적응하기 위해 skip connection을 pooling한다. MHPA는 query pooling 연산자 $\mathcal{P}(\cdot; \Theta_Q)$를 residual 경로에 추가하여 이러한 불일치를 처리한다. MHPA의 입력 $X$를 출력에 직접 추가하는 대신 pooling된 입력 $X$를 출력에 추가하여 attend된 query $Q$와 해상도를 일치시킨다.
Stage 변경 간의 채널 차원 불일치를 처리하기 위해 MHPA 연산의 layer-normalize된 출력에서 연산하는 추가 linear layer를 사용한다. 이는 정규화되지 않은 신호에서 작동하는 다른 skip connection과 다르다.
3. Network instantiation details
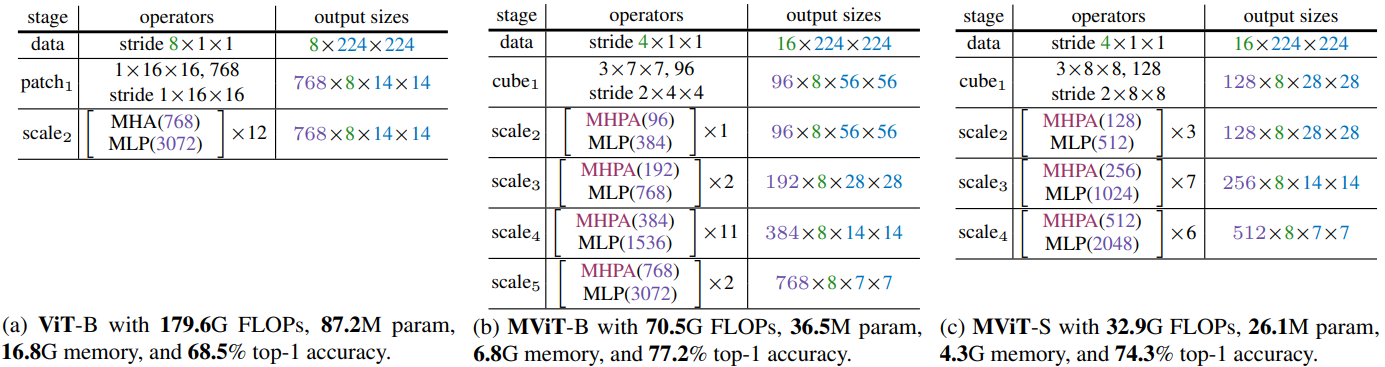
위 표는 ViT와 MViT에 대한 기본 모델의 구체적인 인스턴스화를 보여준다. ViT-Base (a)는 처음에 입력을 차원 $D = 768$의 1$\times$16$\times$16 모양 패치에 project한 다음 $N = 12$개의 transformer 블록을 쌓는다. 8$\times$224$\times$224 입력의 경우 해상도는 모든 레이어에서 768$\times$8$\times$14$\times$14로 고정된다. 시퀀스 길이 (시공간 해상도 + 클래스 토큰)는 8$\times$14$\times$14 + 1 = 1569이다.
MViT-Base (b)는 4개의 scale stage로 구성되어 있으며 각 stage에는 일관된 채널 크기의 여러 transformer 블록이 있다. MViT-B는 처음에 3$\times$7$\times$7 모양의 중첩된 시공간 큐브를 사용하여 $D = 96$의 채널 차원에 입력을 project한다. 길이 8$\times$56$\times$56 + 1 = 25089의 결과 시퀀스는 각 추가 stage에 대해 4배로 줄어들어 scale4에서 최종 시퀀스 길이는 8$\times$7$\times$7 + 1 = 393이 된다. 동시에 채널 차원은 각 단계에서 2배로 업샘플링되어 scale4에서 768로 증가한다. 모든 pooling 연산과 이에 따른 해상도 다운샘플링은 처리된 클래스 토큰 임베딩을 포함하지 않고 데이터 시퀀스에서만 수행된다.
scale1 stage에서 MHPA head 수를 $h = 1$로 설정하고 채널 차원으로 head 수를 늘린다 (head당 채널 $D/h$는 96으로 일정하게 유지됨). 각 stage 전환에서 이전 stage의 출력 MLP 차원은 2배로 증가하고 $Q$ 텐서의 MHPA는 다음 stage의 입력에서 $s^Q = (1, 2, 2)$로 pooling한다.
모든 MHPA 블록에서 $K$, $V$ pooling을 사용하고 scale1에서 $\Theta_K \equiv \Theta_V$와 $s^Q = (1, 8, 8)$을 사용하고 이 stride를 적응적으로 감소시킨다. $K$, $V$ 텐서가 모든 블록에서 일관된 스케일을 갖도록 stage 전체에 걸쳐 스케일을 조정한다.
Experiments: Video Recognition
- 데이터셋: Kinetics-400 (K400), Kinetics-600 (K600), Something-Something-v2, Charades, AVA
1. Main Results
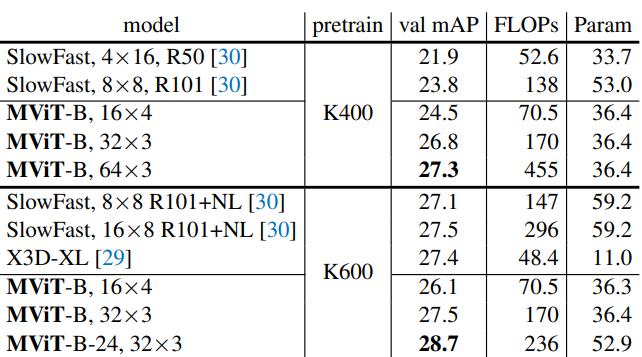
다음은 Kinetics-400에서 이전 연구들과 비교한 표이다.

다음은 Kinetics-600에서 이전 연구들과 비교한 표이다.
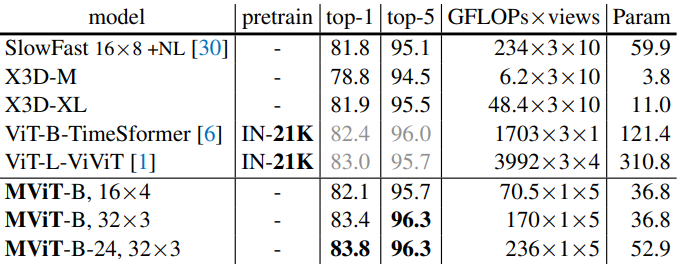
다음은 SSv2에서 이전 연구들과 비교한 표이다.
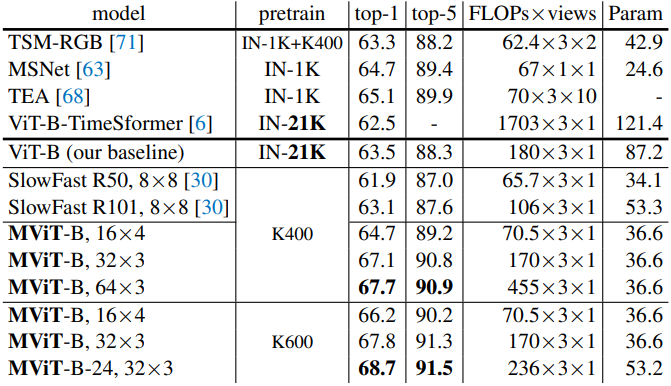
다음은 Charades에서 이전 연구들과 비교한 표이다.
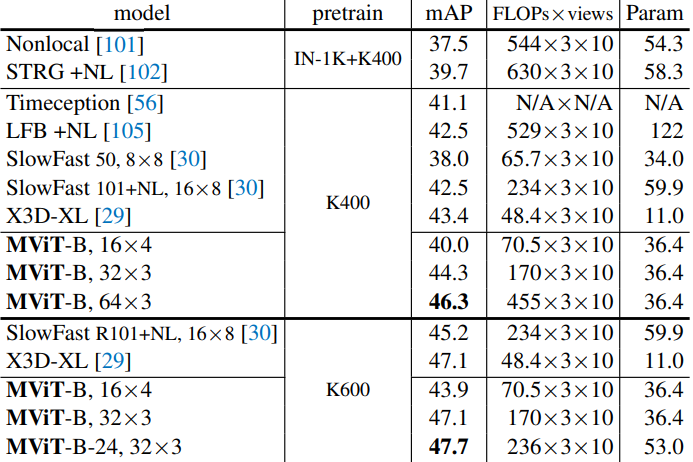
다음은 AVA v2.2에서 이전 연구들과 비교한 표이다.
2. Ablations on Kinetics
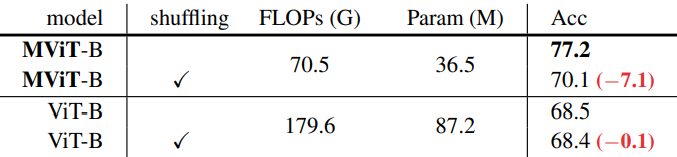
다음은 프레임 셔플링에 대한 ablation study이다.
다음은 query 및 key-value pooling에 대한 ablation study이다. (ViT-B)

다음은 시간-공간 위치 임베딩 분리에 대한 ablation study이다.

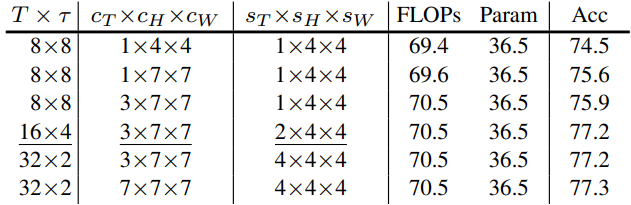
다음은 입력 샘플링에 대한 ablation study이다.
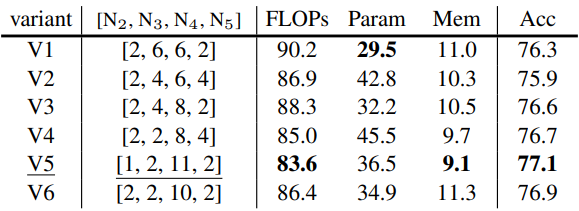
다음은 stage 설정에 대한 ablation study이다. (MViT-B)
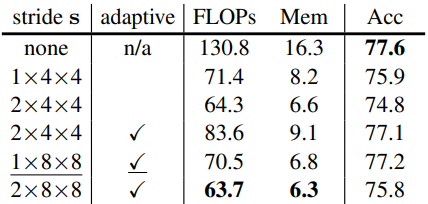
다음은 key-value pooling에 대한 ablation study이다.
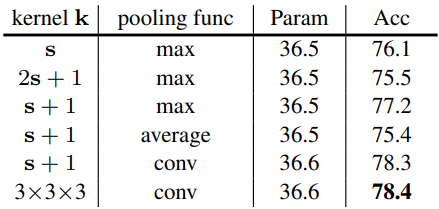
다음은 pooling 함수에 대한 ablation study이다.
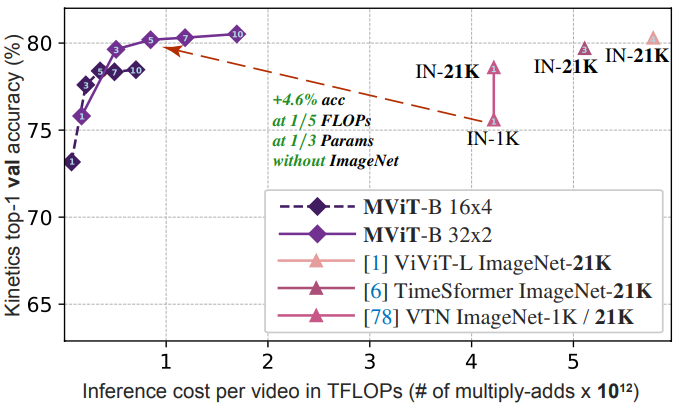
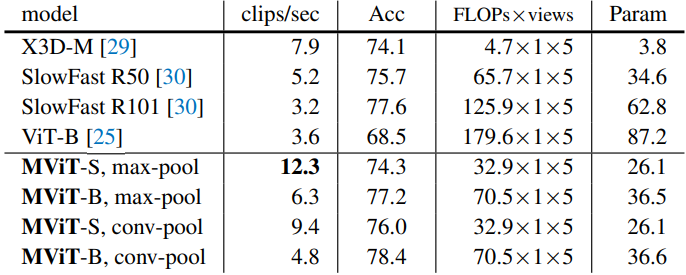
다음은 Kinetics-400에서의 속도-정확도 trade-off이다.
Experiments: Image Recognition
- 데이터셋: ImageNet-1K
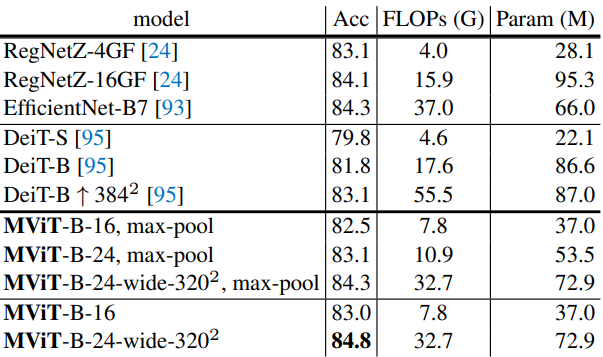
다음은 ImageNet에서 이전 연구들과 비교한 표이다.