[논문리뷰] Zero-Shot Novel View and Depth Synthesis with Multi-View Geometric Diffusion

CVPR 2025. [Paper] [Page]
Vitor Guizilini, Muhammad Zubair Irshad, Dian Chen, Greg Shakhnarovich, Rares Ambrus
Toyota Research Institute
30 Jan 2025

Introduction

본 논문은 새로운 뷰와 depth map을 조건부 생성 task로 직접 렌더링하는 것을 목표로 한다. 지금까지의 새로운 뷰 합성을 위한 diffusion 기반 방법은 더 간단한 설정이나 다운스트림 3D 재구성을 위한 2D prior로 제한되었다. 이는 중간 3D 장면 표현 없이 새로운 뷰를 생성할 때 멀티뷰 일관성을 적용하는 것이 어렵기 때문이다. 이 문제에 대한 본 논문의 해결책은 raymap conditioning을 통해 입력 뷰와 입력 카메라에 대한 직접 컨디셔닝을 사용하여 새로운 뷰와 깊이 합성의 공동 task를 위한 하나의 diffusion model을 학습시키는 것이다. 이를 통해 중간 3D 표현이나 특별한 메커니즘 없이도 scale이 정확하고 멀티뷰에서 일관된 예측을 생성할 수 있다.

저자들은 sparse한 관측으로부터 멀티뷰에서 일관된 3D 장면을 implicit하게 표현하도록 학습하는 모델을 학습시키기 위해, 다양한 시나리오에서 얻은 현실 및 합성 이미지를 포함하여 공개적으로 이용 가능한 데이터셋에서 6천만 개 이상의 멀티뷰 샘플을 선별했다. 이러한 다양한 데이터를 적절히 활용하여 효과적으로 학습하기 위한 새로운 기법을 도입했다.

1. Sparse할 수 있는 현실 깊이를 처리하기 위해 효율적인 transformer 아키텍처를 사용하여 pixel-level diffusion을 수행하여 전용 오토인코더의 필요성을 없앴다.
2. 학습 가능한 task 임베딩을 사용하여 동일하게 컨디셔닝된 latent 토큰에서 어떤 출력을 생성해야 하는지 결정함으로써 깊이 레이블의 유무에 상관없는 통합 학습을 가능하게 하였다.
3. Non-metric 데이터셋을 처리하기 위해, 여러 시점에서 일관된 depth map을 생성하는 새로운 scene scale normalization (SSN) 절차를 제안하였다.

제안된 Multi-View Geometric Diffusion (MVGD) 프레임워크는 여러 벤치마크에서 기존 방법들을 능가하는 성능을 보이며, 다양한 양의 뷰 컨디셔닝(2-9)을 적용한 novel view synthesis에서 SOTA를 확립하였다. MVGD는 100개 이상의 임의 개수의 컨디셔닝 뷰를 처리할 수 있으며, 저자들은 긴 시퀀스에서 멀티뷰 일관성을 더욱 향상시키도록 incremental conditioning 전략을 제안하였다. 또한, 모델 복잡도 증가에 따라 결과가 향상되는 유망한 scaling behavior를 보이며, 더 작은 모델에서 점진적으로 fine-tuning하여 학습 시간을 최대 70%까지 단축할 수 있다.

Method

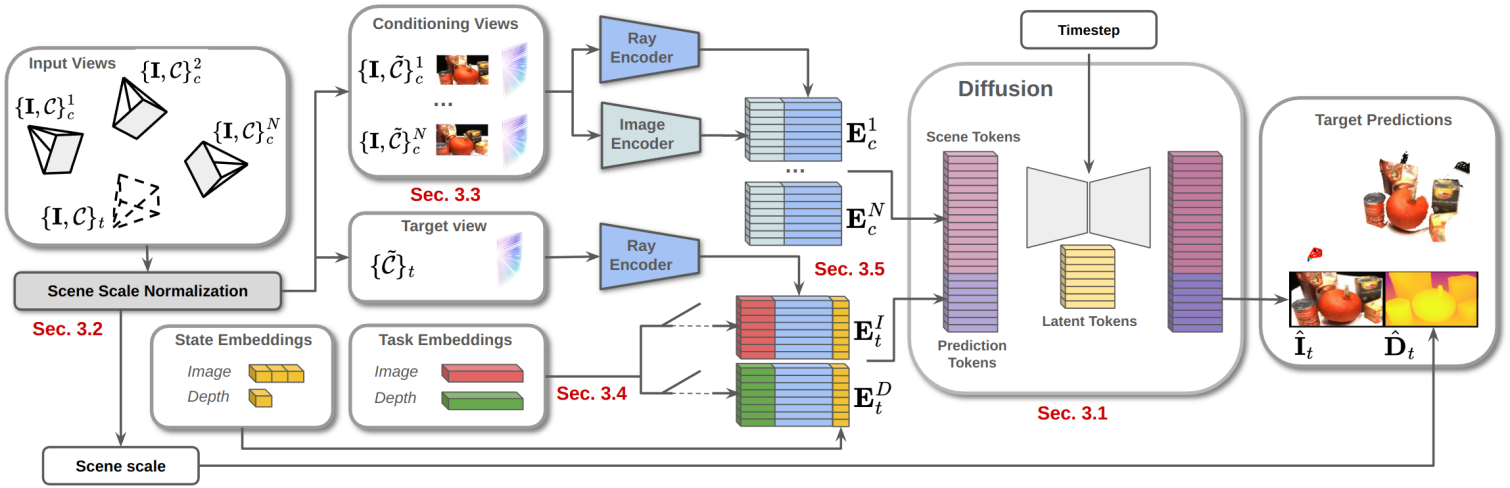
• 입력
  • 이미지 컬렉션 \(\{\textbf{I}_n\}_{n=1}^N\)
  • 카메라 \(\{\mathcal{C}_n\}_{n=1}^N = \{\textbf{K}_n, \textbf{T}_n\}_{n=1}^N\)
    • intrinsics \(\textbf{K}_n \in \mathbb{R}^{3 \times 3}\)
    • extrinsics \(\textbf{T}_n \in \mathbb{R}^{4 \times 4}\)
  • 타겟 카메라 \(\mathcal{C}_t\)
• 목표
  • 이미지 \(\hat{\textbf{I}}_t \in \mathbb{R}^{H \times W \times 3}\)
  • depth map \(\hat{\textbf{D}}_t \in \mathbb{R}^{H \times W}\)

새로운 \(\hat{\textbf{I}}_t\)와 \(\hat{\textbf{D}}_t\)를 샘플링하기 위한 조건부 분포를 학습하기 위해, diffusion model \(f_\theta \sim p (\hat{\textbf{I}}_t, \hat{\textbf{D}}_t \vert \mathcal{C}_t, \{\textbf{I}_n\}_{n=1}^N, \{\mathcal{C}_n\}_{n=1}^N)\)를 사용한다.

1. Scene Scale Normalization

스케일 추정은 본질적으로 모호한 문제이다. 프레임을 하나만 사용하는 방법은 스케일을 직접 추정할 수 없으며, 모호성을 해소하기 위해 다른 소스에 의존해야 한다. 여러 프레임을 사용하는 방법은 형상 구조를 유지하기 위해 extrinsics에서 제공하는 스케일을 상속해야 한다. 이는 추가 센서의 metric 스케일이나 COLMAP의 임의 스케일과 같이 서로 다른 calibration 절차를 사용하는 여러 데이터셋으로 학습시킬 때 특히 어렵다.

저자들은 diffusion process에 대한 입력을 정규화함으로써, 컨디셔닝 카메라와 실제 깊이로부터 장면 스케일을 자동으로 추출하도록 설계된 간단한 기법을 제안하였다. 이 장면 스케일은 생성된 예측에 다시 주입되어 멀티뷰에서 일관된 depth map을 생성한다. 먼저, 모든 컨디셔닝 extrinsics \(\textbf{T}_c^n\)은 새로운 타겟 extrinsics \(\textbf{T}_t\)를 기준으로 표현되므로

\[\begin{equation} \tilde{\textbf{T}}_c^n = \textbf{T}_c^n \textbf{T}_t^{-1} \end{equation}\]

이다. 이는 새로운 정규화된 타겟 카메라 \(\tilde{\mathcal{C}}_t = \{\textbf{K}, \tilde{\textbf{T}}\}_t\)가 항상 원점에 위치함을 의미한다. 이는 장면 수준의 좌표 변화에 대한 translation 및 rotation 불변성을 강화한다.

장면 스케일 $s$를 모든 공간 좌표에서 가장 큰 절대 카메라 translation을 나타내는 스칼라로 정의한다.

\[\begin{equation} s = \max \{\{\vert \tilde{x} \vert, \vert \tilde{y} \vert, \vert \tilde{z} \vert\}_c^n\}_{n=1}^N \\ \textrm{where} \; \textbf{t}_c^n = [x, y, z]^\top, \; \textbf{T}_c^n = \begin{bmatrix} \textbf{R}_c^n & \textbf{t}_c^n \\ \textbf{0} & 1 \end{bmatrix} \end{equation}\]

그런 다음 모든 translation 벡터 \(\textbf{t}_c^n\)를 $s$로 나눈다.

\[\begin{equation} \tilde{\textbf{t}}_c^n = \left[ \frac{x}{s}, \frac{y}{s}, \frac{z}{s} \right]^\top \end{equation}\]

학습 중에, 타겟 depth map \(\textbf{D}_t\)가 GT로 사용되는 경우, 장면 형상을 뷰 전체에서 일관되게 유지하기 위해 $s$로 나누어

\[\begin{equation} \tilde{\textbf{D}}_t = \frac{\textbf{D}_t}{s} \end{equation}\]

가 되도록 한다. \(\tilde{\textbf{D}}_t\)가 모델이 추정할 수 있는 최댓값 $d_\textrm{max}$보다 크면, 정규화된 실제 값이 범위 내에 있도록 장면 스케일을

\[\begin{equation} \textbf{s}^\prime = s \cdot \frac{d_\textrm{max}}{\max \{ \tilde{\textbf{D}}_t \}} \end{equation}\]

로 재계산하고, 이 새로운 값을 사용하여 \(\{\textbf{t}_c^n\}_{n=1}^N\)을 재계산한다.

Inference 과정에서 \(\hat{\textbf{D}}_t\)가 생성되면, 컨디셔닝된 카메라와의 일관성을 유지하기 위해 $s$를 곱한다. 즉, 생성된 depth map은 컨디셔닝된 카메라와 동일한 스케일을 갖게 된다.

2. Conditioning Embeddings

이미지 인코더

EfficientViT를 사용하여 입력 컨디셔닝 뷰를 tokenize하여 새로운 생성을 위한 시각적 장면 정보를 제공한다. 구체적으로, 사전 학습된 EfficientViT-SAM-L2 모델을 기반으로 학습 과정에서 end-to-end fine-tuning을 수행한다.

입력 이미지 $\textbf{I} \in \mathbb{R}^{H \times W \times 3}$은 feature \(\textbf{F}_\textbf{I} \in \mathbb{R}^{\frac{H}{4} \times \frac{W}{4} \times 448}\)가 된다. 이러한 feature들은 flatten되고 linear layer \(\mathcal{L}_{448 \rightarrow D_I}^I\)에 의해 처리되어 이미지 임베딩 \(E_c^{I,n} \in \mathbb{R}^{\frac{HW}{16} \times D_I}\)가 된다. 이 과정은 각 컨디셔닝 뷰에 대해 반복되어 $N$개의 이미지 임베딩을 생성한다.

광선 인코더

푸리에 인코딩을 사용하여 입력 카메라를 tokenize하며, 카메라 $k$의 각 픽셀 \(\textbf{p}_{ij}\)에 대해 원점 \(\textbf{t}_{ijk}\)와 시점 방향 \(\textbf{r}_{ijk}\)를 포함하는 raymap으로 parameterize된다.

\[\begin{aligned} \textbf{t}_{ijk} &= [x, y, z]_k^\top \\ \textbf{r}_{ijk} &= (\textbf{K}_k \textbf{R}_k)^{-1} [u_{ij}, v_{ij}, 1]^\top \end{aligned}\]

이 정보는 3D 공간에서 컨디셔닝 뷰에서 추출한 feature를 배치하고, 이미지 및 깊이 합성을 위한 새로운 뷰를 결정하는 데 사용된다. 컨디셔닝 카메라 \(\mathcal{C}_n\)은 이미지 임베딩의 해상도에 맞게 크기가 조정되고, 타겟 카메라 \(\textbf{C}_t\)는 동일하게 유지돤다. \(\textbf{t}_t\)는 항상 원점에 있고 \(\textbf{R}_t = \textbf{I}\)이다.

원점과 시점 방향에 대한 푸리에 인코딩 주파수를 각각 $N_o$와 $N_r$이라 하면, 광선 임베딩 \(E_c^{R,n} \in \mathbb{R}^{\frac{HW}{16} \times D_R}\)의 차원은 $D_R = 3 (N_o + N_r + 1)$이다.

3. Multi-Task Learning

다른 방법들과 달리 MVGD는 중간 3D 표현을 유지하지 않는다. 대신, implicit model에서 직접 새로운 렌더링을 생성하여 멀티뷰 일관성을 유지한다. 이는 새로운 뷰와 깊이 합성을 함께 학습함으로써, 즉 이미지와 함께 새로운 뷰의 depth map을 직접 렌더링함으로써 달성된다.

간단한 접근법은 RGB-D 예측을 하나의 task로 생성하는 것이다. 그러나 이 경우 학습 데이터셋이 dense한 GT 깊이를 가진 데이터셋으로만 제한된다. 다른 대안은 task별 토큰을 추가하여 latent 토큰 자체를 컨디셔닝하는 것이다. 그러나 이 경우 두 task에 대한 예측을 동시에 생성하는 것이 불가능해지고, latent space의 전용 latent 토큰 부분을 생성하여 appearance prior와 geometric prior를 분리한다. 따라서 학습 가능한 task 임베딩 \(\textbf{E}^\textrm{task} \in \mathbb{R}^{D_\textrm{task}}\)를 사용하여 각 생성이 특정 task를 수행하도록 가이드한다. 모델의 예측은 task에 따라 다음과 같이 parameterize된다.

RGB Parameterization

Pixel-level diffusion에는 오토인코더가 필요하지 않으므로, 실제 이미지는 다음과 같이 간단히 $[-1, 1]$로 정규화된다.

\[\begin{aligned} \textbf{P}_\textrm{RGB} &= \frac{\textbf{I} + 1}{2} \\ \hat{\textbf{I}} &= 2 \hat{\textbf{P}}_\textrm{RGB} + 1 \end{aligned}\]

Depth Parameterization

멀티뷰 일관성을 유지하기 위해 생성된 깊이 예측은 스케일을 반영해야 하며, 따라서 가능한 값의 범위가 넓어야 한다. 저자들은 \(d_\textrm{min} = 0.1\), \(d_\textrm{max} = 200\)으로 가정하여 MVGD가 실내 및 실외 시나리오에 적합하도록 하였다. 이 값들은 장면 스케일 정규화 이후에 고려되므로 metric 값이 아니다.

깊이는 다음과 같이 로그 스케일로 parameterize된다.

\[\begin{aligned} \textbf{P}_D &= 2 \left( \log \left( \frac{\textbf{D}}{s \cdot d_\textrm{min}} \right) / \log \left( \frac{d_\textrm{max}}{d_\textrm{min}} \right)\right) - 1 \\ \hat{\textbf{D}} &= \exp \left( (2 \hat{\textbf{P}}_D + 1) \log \left( \frac{d_\textrm{max}}{d_\textrm{min}} \right) \right) d_\textrm{min} \cdot s \end{aligned}\]

4. Novel View and Depth Synthesis

위에 설명된 단계는 두 가지 서로 다른 입력 세트를 생성한다.

1. 장면 토큰: diffusion process가 장면을 이해하는 데 사용
2. 예측 토큰: 원하는 예측을 생성하도록 diffusion process를 가이드하는 데 사용

장면 토큰은 각 컨디셔닝 뷰에서 이미지 임베딩과 광선 임베딩을 먼저 concat한 다음, 모든 컨디셔닝 뷰에서 임베딩을 concat하여 얻는다.

\[\begin{aligned} \textbf{E}_c^n &= \textbf{E}_c^{I,n} \oplus \textbf{E}_c^{R,n} \in \mathbb{R}^{\frac{HW}{16} \times (D_I + D_R)} \\ \textbf{E}_c &= \textbf{E}_c^1 \oplus \cdots \oplus \textbf{E}_c^N \in \mathbb{R}^{\frac{NHW}{16} \times (D_I + D_R)} \end{aligned}\]

학습 효율성을 높이기 위해 컨디셔닝으로 $M_s$개의 장면 토큰을 무작위로 샘플링한다.

예측 토큰은 타겟 카메라의 광선 임베딩 \(\mathbb{E}_t^R\)를 원하는 task 임베딩 \(\mathbb{E}^\textrm{task}\)와 상태 임베딩 \(\textbf{S}_t^\textrm{task}\)와 concat하여 얻는다. 상태 임베딩에는 diffusion model 예측에 대한 진화하는 상태가 포함되어 있으며, 다음과 같이 정의된다.

학습

상태 임베딩 \(\textbf{S}_t\)는 입력 이미지 \(\textbf{I}_t\) 또는 depth map \(\textbf{D}_t\)를 parameterize한 것이며, 무작위로 샘플링된 timestep $t \in [1, T]$가 주어졌을 때 noise scheduler $n(t)$에 의해 결정된 랜덤 noise가 추가된다. 이미지 생성과 깊이 생성을 각각 학습시키기 위해 L2 loss외 L1 loss를 사용한다. 깊이 추정을 위해 유효한 GT를 가진 픽셀에 대해서만 예측 토큰을 생성한다. 두 task 모두 효율성을 높이기 위해 $M_p$개의 예측 토큰을 무작위로 샘플링한다.

Inference

상태 임베딩 \(\textbf{S}_t^T \sim \mathcal{N} (0,I)\)은 이미지 생성을 위한 3차원 벡터 또는 깊이 생성을 위한 스칼라로 샘플링된다. $T$ step 동안 반복적으로 noise를 제거하여 $t = 0$에서의 상태 임베딩 \(\textbf{S}_t^0\)을 구하고, \(\textbf{S}_t^0\)은 \(\hat{\textbf{I}}_t\) 또는 \(\hat{\textbf{D}}_t\)로 다시 변환된다. 확률론적 문제를 완화하기 위해 5개의 샘플에 대해 test-time 앙상블을 수행한다.

5. Incremental Multi-View Generation

Diffusion process의 확률성으로 인해, 관측되지 않은 영역에서 여러 예측을 생성하면 각 예측이 동등하게 유효하더라도 불일치가 발생할 수 있다. 이러한 모호성을 해결하기 위해 생성된 이미지의 이력 \(\{\hat{\textbf{I}}, \mathcal{C}\}_{g=1}^G\)을 유지하여 향후 생성을 위한 추가 조건으로 사용한다. 이 접근법은 추가적인 장면 토큰을 생성하지만, latent 토큰의 수는 동일하게 유지되어 효율성을 크게 향상시킨다. 실제로, 하나의 GPU에서 수천 개의 뷰로 확장될 수 있으며, 이는 추가 정보 없이도 추가적인 개선을 가능하게 한다.

6. Fine-Tuning Larger Models

Latent 토큰 $\textbf{Z}$의 고정된 차원은 입력 토큰 $\textbf{X}$의 개수 측면에서 효율적인 학습 및 inference를 가능하게 한다. 그러나 이러한 표현은 특히 대규모 학습을 고려할 때 생성된 샘플의 품질을 저해할 수 있다. 이 가설이 맞다면 latent 토큰의 개수를 늘리면 학습 시간이 느려지지만 개선 효과가 있을 것이다.

Latent 토큰을 더 많이 도입하더라도 아키텍처는 전혀 변경되지 않는다. 즉, 입력과의 cross-attention과 latent 토큰 간의 self-attention은 동일하게 유지된다. 따라서 더 큰 모델을 처음부터 학습하는 것을 피하기 위해, 특정 개수의 latent 토큰으로 학습한 후에는 단순히 복제하고 concat하여 구조적으로 유사하지만 용량은 두 배인 표현을 얻을 수 있다. 이렇게 더 큰 모델을 더욱 최적화할 수 있으며, 이러한 점진적인 fine-tuning 전략이 새로운 모델을 처음부터 학습하지 않고도 상당한 개선 효과를 가져온다.

Experiments

• 아키텍처 디테일
  • base model: RIN
    • block 6개, 깊이 4
    • latent 16개, \(\textbf{Z} \in \mathbb{R}^{256 \times 1024}\)
  • 광선 임베딩: $N_o$ = $N_r$ = 8, 최대 주파수 = 100
  • Task 임베딩: $D_\textrm{task}$ = 128, $D_I$ = 256
  • 토큰 수: $M_s$ = 1,024, $M_p$ = 4,096
  • 학습 컨디셔닝 뷰 수: 2~5
  • DDIM
    • timestep: 학습은 1,000, inference는 10
    • noise schedule: sigmoid
    • EMA 사용 ($\beta$ = 0.999)
  • optimizer: AdamW (\(\beta_1\) = 0.9, \(\beta_2\) = 0.99)
  • batch size: 512
  • weight decay: 0.01
  • learning rate: $10^{-4}$ (1만 step linear warm-up, cosine decay)
  • 총 학습 step: 30만
  • GPU: 약 6천 A100 GPU-hour

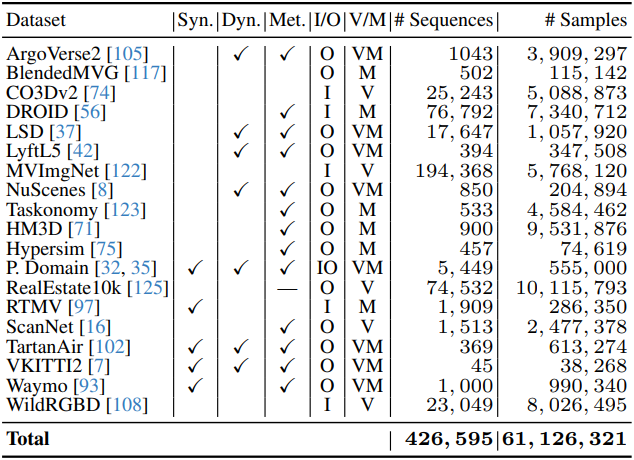
학습 데이터셋은 아래 표와 같다.

1. Novel View Synthesis

다음은 새로운 뷰 및 깊이 합성의 예시들이다.

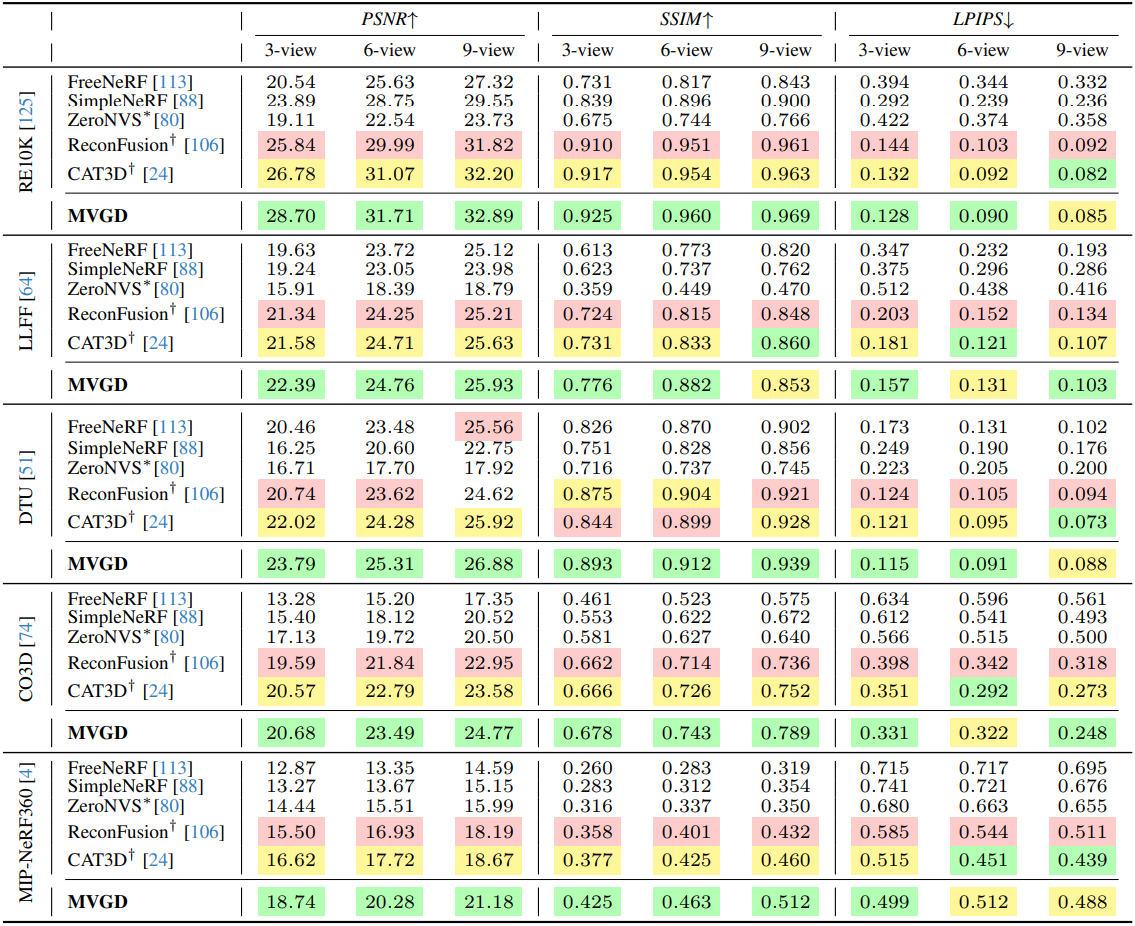
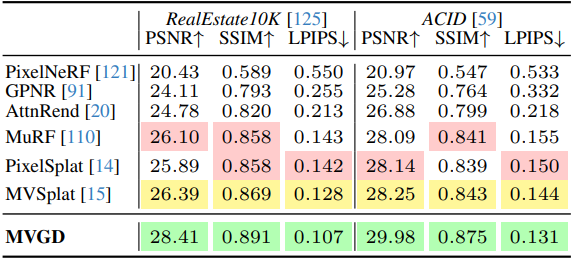
다음은 novel view synthesis 결과를 비교한 것이다. (조건 뷰: 위 3~9개, 아래 2개) 건

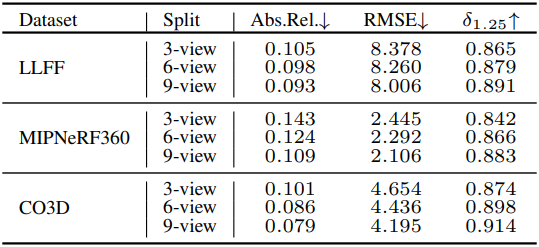
다음은 깊이 합성 결과이다. (조건 뷰: 3~9개)

2. Multi-View Depth Estimation

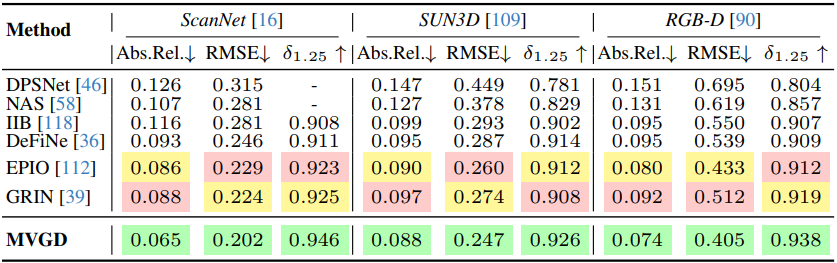
다음은 stereo depth 예측 결과를 비교한 것이다. (조건 뷰: 2개)

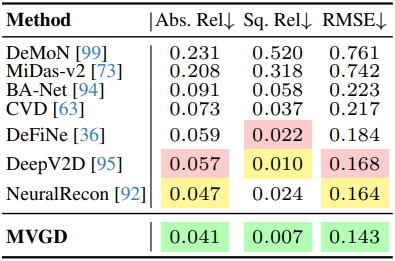
다음은 ScanNet에서의 동영상 깊이 예측 결과를 비교한 것이다. (조건 뷰: 10개)

3. Incremental Fine-Tuning

다음은 incremental fine-tuning에 따른 성능을 비교한 것이다.

4. Ablation Study

다음은 ablation 결과이다.