[논문리뷰] Simple and Controllable Music Generation (MusicGen / Audiocraft)

NeurIPS 2023. [Paper] [Github]
Jade Copet, Felix Kreuk, Itai Gat, Tal Remez, David Kant, Gabriel Synnaeve, Yossi Adi, Alexandre Défossez
Meta AI
8 Jun 2023

Introduction

Text-to-music은 텍스트 설명이 주어진 음악 작품을 생성하는 task이다. 음악을 생성하는 것은 긴 범위의 시퀀스를 모델링해야 하므로 어려운 task이다. 음성과 달리 음악은 전체 주파수 스펙트럼을 사용해야 한다. 즉, 더 높은 속도로 신호를 샘플링한다는 의미이다. 즉, 음악 녹음의 표준 샘플링 속도는 음성의 경우 16kHz인 것에 비해 44.1kHz 또는 48kHz이다. 또한 음악에는 다양한 악기의 화음과 선율이 포함되어 있어 복잡한 구조를 만든다. 인간은 부조화에 매우 민감하므로 음악을 생성해도 멜로디 오차가 작아야한다. 마지막으로, 조(key), 악기, 선율, 장르 등 다양한 방식으로 생성 과정을 제어하는 능력은 음악 제작자에게 필수적이다.

Self-supervised 방식의 오디오 표현 학습, 순차 모델링, 오디오 합성의 최근 발전은 이러한 모델을 개발할 수 있는 조건을 제공한다. 오디오 모델링을 보다 다루기 쉽게 만들기 위해 최근 연구에서는 동일한 신호를 나타내는 개별 토큰의 여러 스트림으로 오디오 신호를 나타내는 것을 제안했다. 이를 통해 고품질 오디오 생성과 효과적인 오디오 모델링이 모두 가능하다. 그러나 이것은 여러 병렬 종속 스트림을 공동으로 모델링하는 비용이 든다.

본 논문에서는 텍스트 설명을 통해 고품질 음악을 생성할 수 있는 간단하고 제어 가능한 음악 생성 모델인 MusicGen을 소개한다. 본 논문은 이전 연구들의 일반화 역할을 하는 음향 토큰의 여러 병렬 스트림을 모델링하기 위한 일반적인 프레임워크를 제안한다. 생성된 샘플의 제어 가능성을 개선하기 위해 supervise되지 않은 멜로디 컨디셔닝을 추가로 도입하여 모델이 주어진 하모닉 및 멜로디 구조와 일치하는 음악을 생성할 수 있도록 한다.

Method

MusicGen은 autoregressive Transformer 기반 디코더로 구성되어 있으며 텍스트 또는 멜로디 표현을 기반으로 한다. 언어 모델은 EnCodec 오디오 토크나이저의 양자화된 unit 위에 있으며, 낮은 프레임 속도의 이산적인 표현에서 충실도 높은 재구성을 제공한다. High Fidelity Neural Audio Compression와 같은 압축 모델은 Residual Vector Quantization (RVQ)를 사용하여 여러 병렬 스트림을 생성한다. 이 설정에서 각 스트림은 서로 다른 학습된 코드북에서 발생하는 개별 토큰으로 구성된다. 이전 연구들에서는 이 문제를 처리하기 위해 몇 가지 모델링 전략을 제안했다. 본 논문에서는 다양한 codebook interleaving pattern으로 일반화되는 새로운 모델링 프레임워크를 소개하고 몇 가지 변형을 탐색한다. 패턴을 통해 양자화된 오디오 토큰의 내부 구조를 활용할 수 있다. 마지막으로 MusicGen은 텍스트 또는 멜로디를 기반으로 조건부 생성을 지원한다.

1. Audio tokenization

Residual Vector Quantization (RVQ)을 사용하여 양자화된 latent space와 adversarial reconstruction loss가 있는 convolution autoencoder인 EnCodec을 사용한다. 참조 오디오 확률 변수 $X \in \mathbb{R}^{d \cdot f_s}$가 주어지면 ($d$는 오디오 지속 시간, $f_s$는 샘플 속도) EnCodec은 이를 프레임 속도 $f_r \ll f_s$로 연속 텐서로 인코딩한다. 그런 다음 이 표현은 \(Q \in \{1, \cdots, N\}^{K \times d \cdot f_r}\)로 양자화되며, $K$는 RVQ에서 사용되는 코드북의 수이고 $N$은 코드북의 크기이다. 양자화 후에 오디오 샘플을 나타내는 각각의 길이가 $T = d \cdot f_r$인 $K$개의 병렬 이산 토큰 시퀀스가 남는다. RVQ에서 각 quantizer는 이전 quantizer가 남긴 양자화 오차를 인코딩하므로 서로 다른 코드북에 대한 양자화 값은 일반적으로 독립적이지 않으며 첫 번째 코드북이 가장 중요하다.

2. Codebook interleaving patterns

Exact flattened autoregressive decomposition

Autoregressive model에는 이산적인 랜덤 시퀀스 \(U \in \{1, \cdots, N\}^S\)가 필요하다 ($S$는 시퀀스 길이). 규칙에 따라 시퀀스의 시작을 나타내는 deterministic한 특수 토큰인 $U_0 = 0$을 사용한다. 그런 다음 분포를 다음과 같이 모델링할 수 있다.

\[\begin{equation} \forall t > 0, \quad p_t (U_{t-1}, \cdots, U_0) = \mathbb{P}[U_t \vert U_{t-1}, \cdots, U_0] \end{equation}\]

재귀적으로 $\widetilde{U}_0 = 0$을 정의하고, 모든 $t > 0$에 대해

\[\begin{equation} \forall t > 0, \quad \mathbb{P} [\widetilde{U}_t] = p_t (\widetilde{U}_{t-1}, \cdots, \widetilde{U}_0) \end{equation}\]

가 성립한다고 하자. 그러면 즉시 $U$와 $\widetilde{U}$가 동일한 분포를 따른다. 이는 $p$의 완벽한 모델 $\hat{p}$를 피팅할 수 있다면 $U$의 분포를 정확히 맞출 수 있음을 의미한다.

앞에서 언급했듯이 EnCodec 모델에서 얻은 표현 $Q$의 주요 문제는 각 timestep에 대해 $K$개의 코드북이 있다는 것이다. 한 가지 해결책은 $Q$를 평탄화하여 $S = df_s \cdot K$를 취하는 것이다. 즉, 먼저 첫 번째 timestep의 첫 번째 코드북을 예측한 다음 첫 번째 timestep의 두 번째 코드북 등을 예측한다. 그러면 위의 두 식들을 사용하여 이론적으로 $Q$ 분포의 정확한 모델을 피팅할 수 있다. 그러나 단점은 복잡성이 증가하고, 가장 낮은 샘플 속도 $f_r$에서 오는 이득의 일부가 손실된다는 것이다.

하나 이상의 가능한 평탄화가 존재하며 단일 모델을 통해 모든 $\hat{p_t}$ 함수를 추정할 필요는 없다. 예를 들어, MusicLM은 두 가지 모델을 사용한다. 하나는 첫 번째 모델의 결정에 따라 평탄화된 처음 $K/2$개의 코드북을 모델링하고 다른 하나는 나머지 $K/2$개의 평탄화된 코드북을 모델링한다. 이 경우 autoregressive step의 수는 여전히 $df_s \cdot K$이다.

Inexact autoregressive decomposition

또 다른 가능성은 일부 코드북이 병렬로 예측되는 autoregressive decomposition을 고려하는 것이다. 예를 들어, $V_0 = 0$이고 모든 \(t \in \{1, \cdots, N\}\)와 \(k \in \{1, \cdots, K\}\)에서 $V_{t,k} = Q_{t,k}$인 또다른 시퀀스를 정의하자. 코드북 인덱스 $k$를 삭제할 때, 예를 들어 $V_t$를 삭제할 때, 시간 $t$에서 모든 코드북의 연결을 의미한다.

\[\begin{equation} p_{t,k} (V_{t-1}, \cdots, V_0) = \mathbb{P} [V_{t,k} \vert V_{t-1}, \cdots, V_0] \end{equation}\]

재귀적으로 $\widetilde{V}_0 = 0$을 정의하고, 모든 $t > 0$에 대해

\[\begin{equation} \forall t > 0, \quad \mathbb{P} [\widetilde{V}_t] = p_t (\widetilde{V}_{t-1}, \cdots, \widetilde{V}_0) \end{equation}\]

가 성립한다고 하자. $\widetilde{U}$와 달리, 정확한 분포 $p_{t,k}$에 접근할 수 있다고 가정하더라도 $\widetilde{V}$가 $V$와 동일한 분포를 따르는 일반적인 경우를 더 이상 가지지 않는다. 사실, 모든 $t$에 대해 \((V_{t,k})_k\)가 $V_{t−1}, \cdots, V_0$에 대해 조건부로 독립인 경우에만 적절한 생성 모델을 갖게 된다. $t$가 증가함에 따라 오차가 복잡해지고 두 분포가 더 멀어질 수 있다. 이러한 decomposition는 정확하지 않지만, 특히 긴 시퀀스의 경우 원래 프레임 속도를 유지할 수 있어 학습 속도와 inference 속도를 상당히 높일 수 있다. 흥미롭게도 VALL-E의 음성 생성 모델은 부정확한 autoregressive decomposition을 사용한다. 먼저 모든 timestep에 대한 첫 번째 코드북을 순차적으로 예측한 다음 나머지 모든 코드북을 병렬로 예측한다. 모든 timestep에 대해 첫 번째 코드북에서 조건부로 독립적이라고 암시적으로 가정한다.

Arbitrary codebook interleaving patterns

이러한 다양한 decomposition을 실험하고 부정확한 decomposition 사용의 영향을 정확하게 측정하기 위해 codebook interleaving patterns을 도입한다.

\[\begin{equation} \Omega = \{(t, k) : \{1, \cdots, d \cdot f_r \}, k \in \{1, \cdots, K\}\} \end{equation}\]

를 모든 timestep과 코드북 인덱스 쌍의 집합이라고 하자. 코드북 패턴은 시퀀스

\[\begin{equation} P = (P_0, P_1, P_2, \cdots, P_S) \end{equation}\]

이며 $P_0 = \emptyset$이고 모든 $0 < i \le S$, $P_i \subset \Omega$에 대해 $P$는 $\Omega$의 파티션이다. $P_0, P_1, \cdots, P_T$의 모든 위치에 대해 조건부로 $P_t$의 모든 위치를 병렬로 예측하여 $Q$를 모델링한다. 실용적으로 각 코드북 인덱스가 $P_s$에서 최대 한 번 나타나는 패턴으로 제한한다.

이제 다음과 같이 여러 가지 decomposition을 쉽게 정의할 수 있다.

\[\begin{equation} P_s = \{(s, k) : k \in \{1, \cdots, K\}\} \end{equation}\]

비슷하게, VALL-E의 패턴은 다음과 같이 정의할 수 있다.

\[\begin{equation} \begin{cases} P_s = \{(s,1)\} & \quad \textrm{if } s \le T P_s = \{(s,k) : k \in \{2, \cdots, K\}\} & \quad \textrm{otherwise} \end{cases} \end{equation}\]

코드북 사이에 “딜레이”를 도입하는 것도 가능하다.

\[\begin{equation} P_s = \{(s-k+1, k) : k \in \{1, \cdots, K\}, s - k \ge 0\} \end{equation}\]

3. Model conditioning

Text conditioning

입력 오디오 $X$와 일치하는 텍스트 설명이 주어지면 조건 텐서 $C \in \mathbb{R}^{T_C \times D}$를 계산한다. 여기서 $D$는 autoregressive model에서 사용되는 내부 차원이다. 일반적으로 조건부 오디오 생성을 위해 텍스트를 나타내는 세 가지 주요 접근 방식이 있다.

1. T5 encoer: 사전 학습된 텍스트 인코더
2. FLAN-T5: 명령어 기반 언어 모델
3. CLAP: 텍스트-오디오 공동 표현 사용

Melody conditioning

텍스트는 오늘날 조건부 생성 모델에서 두드러진 접근 방식이지만 음악에 대한 보다 자연스러운 접근 방식은 다른 오디오 트랙의 멜로디 구조나 심지어 휘파람이나 흥얼거림을 조건으로 하는 것이다. 이러한 접근 방식을 통해 모델 출력을 반복적으로 개선할 수도 있다. 이를 지원하기 위해 입력의 크로마그램과 텍스트 설명으로 동시에 컨디셔닝하여 멜로디 구조를 제어한다. 예비 실험에서 저자들은 크로마그램에 대한 컨디셔닝이 종종 원래 샘플을 재구성하여 overfitting을 초래한다는 것을 관찰했다. 이를 줄이기 위해 각 timestep에서 우세한 시간-주파수 bin을 선택하여 information bottleneck을 도입한다. 본 논문에서는 unsupervised 접근 방식을 사용하여 supervise된 데이터에 대한 요구 사항을 제거한다.

4. Model architecture

Codebook projection and positional embedding

코드북 패턴이 주어지면 각 패턴 step $P_s$에는 일부 코드북만 존재한다. $Q$에서 $P_s$의 인덱스에 해당하는 값을 검색g한다. 앞서 언급한 바와 같이 각 코드북은 $P_s$에 최대 한 번만 존재하거나 전혀 존재하지 않는다. 존재하는 경우 $N$개의 entry가 있고 차원이 $D$인 학습된 임베딩 테이블을 사용하여 $Q$의 관련 값을 나타낸다. 그렇지 않으면 부재(absence)를 나타내는 특수 토큰을 사용한다. 이 변환 후 각 코드북의 기여도를 합산한다. $P_0 = \emptyset$이므로 첫 번째 입력은 항상 모든 특수 토큰의 합계이다. 마지막으로 현재 step을 인코딩하기 위해 sinusoidal embedding을 더한다.

Transformer decoder

입력은 $L$개의 레이어가 있고 차원이 $D$인 Transformer로 공급된다. 각 레이어는 causal self-attention block으로 구성된다. 그런 다음 컨디셔닝 신호 $C$가 공급되는 cross-attention block을 사용한다. 멜로디 컨디셔닝을 사용할 때 컨디셔닝 텐서 $C$를 Transformer 입력의 prefix로 대신 제공한다. 레이어는 $D$에서 $4D$ 채널까지의 linear layer, ReLU, 다시 $D$ 채널까지의 linear layer로 구성된 fully-connected block으로 끝난다. Attention block과 fully-connected block은 residual skip connection으로 래핑된다. Layer normalization은 residual skip connection과 합산되기 전에 각 block에 적용된다 (pre-norm).

Logits prediction

패턴 step $P_s$에서 Transformer decoder의 출력은 $P_{s+1}$에 의해 주어진 인덱스에서 취한 $Q$ 값에 대한 로짓 예측으로 변환된다. 각 코드북은 $P_{s+1}$에 최대 한 번만 존재한다. 코드북이 있는 경우 $D$ 채널부터 $N$ 채널까지 코드북용 linear layer로 적용하여 logit 예측을 얻는다.

Experiments

• 모델 및 hyperparameter
  • Audio tokenization model
    • non-causal 5 layers EnCodec model 사용
    • 32kHz, stride 640, 최종 frame rate 50Hz
    • 초기 hidden size는 64이고 각 레이어마다 2배가 됨
    • 1초 간격의 오디오로 학습됨
  • Transformer model
    • 메모리 효율적인 Flash attention 사용
    • 30초 간격의 오디오로 학습됨
    • AdamW optimizer, batch size 192, $\beta_1 = 0.9$, $\beta_2 = 0.95$
    • weight decay 0.1, gradient clipping 0.1
    • 300M model의 경우 D-Adaptation 기반 자동 step size 사용 (더 큰 모델은 효과가 없었다고 함)
    • cosine learning rate 사용 (warm-up 4,000 step)
    • exponential moving average 사용 (decay = 0.99)
    • 샘플링 시 top-k sampling 사용 (250 토큰, temperature = 1.0)
  • Text preprocessing
    • AudioGen의 text-normalization 사용
  • Codebook patterns and conditioning
    • “delay” interleaving pattern 사용
    • 30초의 오디오가 1,500개의 autoregressive step으로 변환됨
    • 멜로디 컨디셔닝의 경우 크로마그램 계산에 window size $2^14$, hop size $2^12$ 사용
    • 각 timestep에서 argmax를 취해 크로마그램을 양자화
    • logit 샘플링에 classifier-free guidance 적용 (학습 중에 20%로 컨디셔닝 제거, guidance scale 3.0)
• 데이터셋: 총 2만 시간의 음악 (내부 데이터셋, ShutterStock, Pond5 사용)
• Metric
  • Fréchet Audio Distance (FAD)
  • KL-Divergence (KL)
  • CLAP score (CLAP)

1. Comparison with the baselines

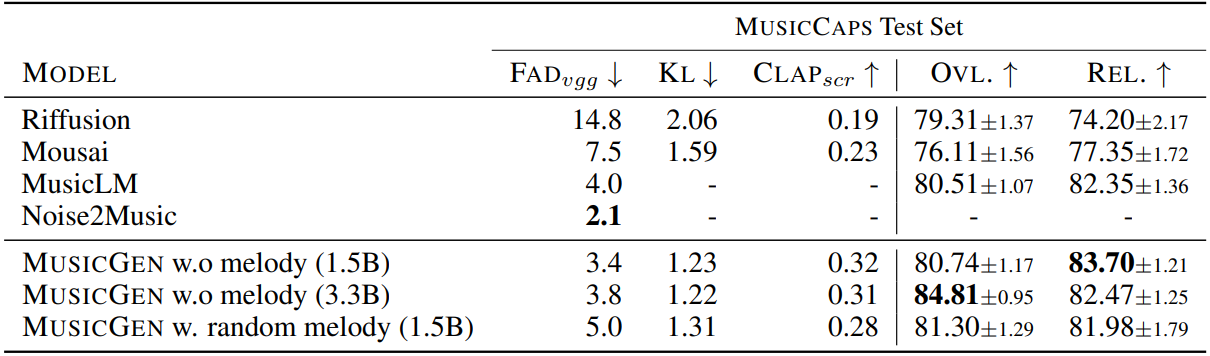
2. Melody evaluation

3. Ablation

The effect of the codebook interleaving patterns

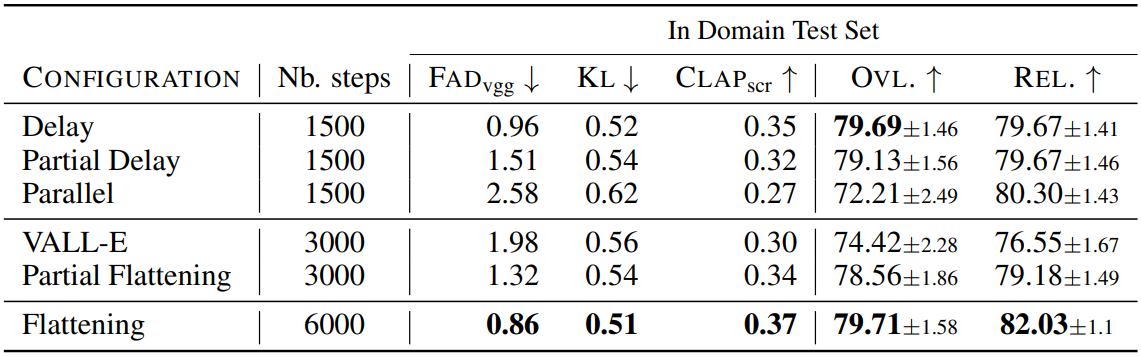
The effect of model size