[논문리뷰] MultiDiffusion: Fusing Diffusion Paths for Controlled Image Generation

ICML 2023. [Paper] [Page] [Github]
Omer Bar-Tal, Lior Yariv, Yaron Lipman, Tali Dekel
Weizmann Institute of Science
16 Feb 2023

Introduction

Text-to-image 생성 모델은 텍스트 프롬프트에서 고품질의 다양한 이미지를 합성하는 전례 없는 능력을 보여주는 “파괴적 기술”로 부상했으며, 현재 diffusion model이 SOTA으로 확립되어 있다. 이러한 발전은 디지털 콘텐츠를 생성하는 방식을 변화시키는 큰 가능성을 제시하지만, 생성된 콘텐츠에 대한 직관적인 제어를 사용자에게 제공하기 어렵기 때문에 text-to-image 모델을 실제 애플리케이션에 배포하는 것은 여전히 어려운 일이다. 현재 diffusion model에 대한 제어 가능성은 두 가지 방법으로 달성된다.

1. 처음부터 모델을 학습하거나 당면한 task에 대해 주어진 diffusion model을 fine-tuning한다. 모델 및 학습 데이터의 규모가 계속 증가함에 따라 이 접근 방식은 fine-tuning 설정에서도 광범위한 컴퓨팅과 긴 개발 기간이 필요한 경우가 많다.
2. 사전 학습된 모델을 재사용하고 일부 제어된 생성 능력을 추가한다. 이전에는 이러한 방법이 특정 task에 집중되어 맞춤형 방법론을 디자인했다.

본 논문의 목표는 사전 학습된 참조 diffusion model을 제어된 이미지 생성에 적용하는 유연성을 크게 높이는 새로운 통합 프레임워크인 MultiDiffusion을 설계하는 것이다. MultiDiffusion의 기본 아이디어는 일련의 공유 파라미터 또는 제약 조건과 함께 결합된 여러 참조 diffusion process로 구성된 새로운 생성 프로세스를 정의하는 것이다. 더 자세히 말하면, 참조 diffusion model은 생성된 이미지의 서로 다른 영역에 적용되어 각각에 대한 denoising step을 예측한다. 결과적으로 MultiDiffusion은 최소 제곱 최적해를 통해 이러한 모든 step을 조정하는 글로벌한 denoising step을 수행한다.

예를 들어, 정사각형 이미지에 대해 학습된 참조 diffusion model이 주어졌을 때 임의의 종횡비로 이미지를 생성하는 task을 생각해 보자. 각 denoising step에서 MultiDiffusion은 참조 모델이 제공하는 모든 정사각형 crop의 denoising 방향을 융합하고 인근 crop이 공통 픽셀을 공유한다는 사실로 인해 제한을 받아 가능한 한 모든 방향을 밀접하게 따르려고 노력한다. 직관적으로 각 crop이 참조 모델의 실제 샘플이 되도록 권장한다. 각 crop이 서로 다른 denoising 방향으로 이동할 수 있지만 본 논문의 프레임워크는 통합된 denoising step을 생성하므로 고품질의 원활한 이미지를 생성한다.

MultiDiffusion을 사용하면 사전 학습된 참조 text-to-image 모델을 원하는 해상도 또는 종횡비로 이미지를 합성하거나 대략적인 영역 기반 텍스트 프롬프트를 사용하여 이미지를 합성하는 등 다양한 애플리케이션에 활용할 수 있다. 특히, 본 논문의 프레임워크는 공통 생성 프로세스를 사용하여 이러한 task를 동시에 해결할 수 있다. 이러한 task를 위해 특별히 학습된 방법과 비교해도 본 논문의 접근 방식은 SOTA 제어 생성 품질을 달성하였다. 또한 계산 오버헤드 없이 효율적으로 작동한다.

Method

이미지 공간 $\mathcal{I} = \mathbb{R}^{H \times W \times C}$와 조건 공간 $\mathcal{Y}$에서 작동하는 참조 모델 역할을 하는 사전 학습된 diffusion model $\Phi$를 고려하자.

\[\begin{equation} \Phi : \mathcal{I} \times \mathcal{Y} \rightarrow \mathcal{I} \end{equation}\]

가우시안 분포 \(P_\mathcal{I}\)에 대하여 \(I_T \sim P_\mathcal{I}\)로 초기화하고, 조건을 $y \in \mathcal{Y}$로 설정한다. 그러면 diffusion model은 noisy한 이미지 $I_T$를 꺠끗한 이미지 $I_0$로 점진적으로 변환하는 이미지의 시퀀스를 구축한다.

\[\begin{equation} I_T, I_{T-1}, \ldots, I_0, \quad \textrm{s.t.} \quad I_{t-1} = \Phi (I_t \vert y) \end{equation}\]

MultiDiffusion

본 논문의 목표는 학습이나 fine-tuning 없이 $\Phi$를 활용하여 잠재적으로 다른 이미지 공간 $\mathcal{J} = \mathbb{R}^{H^\prime \times W^\prime \times C}$와 조건 공간 $\mathcal{Z}$에서 이미지를 생성하는 것이다. 이를 위해 MultiDiffuser $\Psi$라는 함수로 정의된 MultiDiffusion 프로세스를 정의한다.

\[\begin{equation} \Psi : \mathcal{J} \times \mathcal{Z} \rightarrow \mathcal{J} \end{equation}\]

MultiDiffusion은 diffusion process와 유사하게 일부 초기 noisy한 입력 \(J_T \sim P_\mathcal{J}\)로 시작해서 일련의 이미지를 생성한다. 여기서 \(P_\mathcal{J}\)는 $\mathcal{J}$에 대한 noise 분포이다.

\[\begin{equation} J_T, J_{T-1}, \ldots, J_0, \quad \textrm{s.t.} \quad J_{t-1} = \Psi (J_t \vert z) \end{equation}\]

본 논문의 핵심 아이디어는 $\Psi$를 $\Phi$와 가능한 한 일치하도록 정의하는 것이다. 보다 구체적으로, 타겟 이미지 공간과 참조 이미지 공간 사이의 매핑 집합 $F_i : \mathcal{J} \rightarrow \mathcal{I}$와 조건 공간 사이의 대응되는 매핑 집합 $\lambda_i : \mathcal{Z} \rightarrow \mathcal{Y}$를 정의한다. 여기서 \(i \in = \{1, \ldots, N\}\)이다. 이러한 매핑은 애플리케이션에 따라 다르다. 본 논문의 목표는 모든 MultiDiffuser step $J_{t−1} = \Psi (J_t \vert z)$가 가능한 한 가깝게 $\Phi (I_t^i \vert y_i), i \in [n]$, 즉 $\Phi$의 denoising step을 따르도록 만드는 것이다.

\[\begin{equation} I_t^i = F_i (J_t), \quad y_i = \lambda_i (z) \end{equation}\]

새로운 프로세스는 다음 최적화 문제를 해결하여 얻을 수 있다.

\[\begin{equation} \Psi (J_t \vert z) = \underset{J \in \mathcal{J}}{\arg \min} \mathcal{L}_\textrm{FTD} (J \vert J_t, z) \\ \mathcal{L}_\textrm{FTD} (J \vert J_t, z) = \sum_{i=1}^n \| W_i \otimes [F_i(J) - \Phi (I_t^i \vert y_i)] \|^2 \end{equation}\]

여기서 $W_i \in \mathbb{R}_{+}^{H \times W}$는 픽셀별 가중치이고 $\otimes$는 element-wise 곱셈이다. 직관적으로 FTD loss는 생성된 이미지 $J_t$의 서로 다른 영역 $F_i(J_t)$에 제안된 서로 다른 denoising step $\Phi (I_t^i \vert y_i)$를 최소 제곱 방식으로 조정한다. 아래 그림은 MultiDiffuser의 한 step을 보여준다. Algorithm 2는 MultiDiffusion 샘플링 프로세스를 요약한다.

Closed-form formula

본 논문에서 설명하는 애플리케이션에서 $F_i$는 직접적인 픽셀 샘플로 구성된다 (ex. 이미지 $J_t$에서 crop). 이 경우, FTD loss는 minimizer $J$의 각 픽셀이 모든 diffusion 샘플 업데이트의 가중 평균인 quadratic Least-Squares (LS)이다.

\[\begin{equation} \Psi (J_t \vert z) = \sum_{i=1}^n \frac{F_i^{-1} (W_i)}{\sum_{j=1}^n F_j^{-1} (W_j)} \otimes F_i^{-1} (\Phi (I_t^i \vert y_i)) \end{equation}\]

Properties of MultiDiffusion

$\Psi$의 정의에 대한 주요 동기는 다음과 같은 관찰에서 비롯된다.

\[\begin{equation} F_i (J_T) \sim P_\mathcal{I}, \quad \forall i \in [n] \end{equation}\]

를 만족하는 확률 분포 \(P_\mathcal{J}\)를 선택하고 $J_{t−1} = \Psi (J_t \vert z)$를 계산한다. FTC loss가 0에 도달하면, 즉 \(\mathcal{L}_\textrm{FTD} (J_{t−1} \vert J_t, z) = 0\)이면 다음이 성립한다.

\[\begin{equation} I_{t−1}^i = F_i (J_t) = \Phi (I_t^i \vert y_i) \end{equation}\]

즉, 모든 $i \in [n]$에 대해 $I_t^i$는 diffusion 시퀀스이므로 $I_0^i$는 이미지 공간 $\mathcal{I}$에 대해 $\Phi$로 정의된 분포에 따라 분포된다.

이 성질에 대한 의미는 광범위하다. 하나의 참조 diffusion process를 사용하면 참조 diffusion model과의 일관성을 유지하면서 모델을 재학습할 필요 없이 다양한 이미지 생성 시나리오에 유연하게 적응할 수 있다.

Applications

1. Panorama

본 논문의 프레임워크를 사용하여 이미지 공간 $\mathcal{I}$에서 작동하는 학습된 모델 $\Phi$에서 직접 $H^\prime \ge H$, $W^\prime \ge H$인 이미지 공간 $\mathcal{J}$의 diffusion model을 정의한다. $\mathcal{J} = \mathcal{Y}$로 설정한다 (즉, 주어진 텍스트 프롬프트에 대한 파노라마 이미지 생성). $F_i(J) \in \mathcal{I}$는 이미지 $J$의 $H \times W$ crop이고 $z = \lambda_i (z)$이다. 원본 이미지 $J$를 덮는 $n$개의 crop을 고려한다. $W_i = 1$로 설정하면 다음을 얻는다.

\[\begin{equation} \Psi (J_t, z) = \underset{J \in \mathcal{J}}{\arg \min} \sum_{i=1}^n \| F_i (J) - \Phi (F_i (J), z) \|^2 \end{equation}\]

이는 최소 제곱 문제이며, 그 해는 수치적으로 계산된다.

MultiDiffusion은 참조 모델 $\Phi$에서 제공하는 여러 diffusion 경로를 조정한다. $H \times 4W$의 파노라마를 고려한 위 그림에서 이 속성을 설명한다. 위 그림의 (a)는 겹치지 않는 4개의 crop에 $\Phi$를 독립적으로 적용한 경우의 생성 결과를 보여준다. 예상한 대로, 이는 모델에서 무작위로 추출된 4개의 샘플에 해당하므로 crop 간에 일관성이 없다. 동일한 초기 noise에서 시작하는 생성 프로세스를 통해 초기에 관련이 없는 diffusion 경로를 융합하고 생성을 고품질의 일관된 파노라마 (b)로 유도할 수 있다.

2. Region-based text-to-image-generation

영역 마스크 집합 \(\{M_i\}_{i=1}^n \subset \{0, 1\}^{H \times W}\)와 해당 텍스트 프롬프트 집합 \(\{y_i\}_{i=1}^n \subset \mathcal{Y}^n\)이 주어지면 각 영역별로 원하는 내용을 표현한 고품질 이미지 $I \in \mathcal{I}$를 생성하는 것이 목표이다. 즉, 이미지 세그먼트 $I \otimes M_i$가 $y_i$를 나타내야 한다. MultiDiffusion 프로세스는 조건 공간 $\mathcal{Z} = \mathcal{Y}^n$, 즉 $z = (y_1, \ldots, y_n)$에 대해 정의되며 타겟 이미지 공간 $\mathcal{J} = \mathcal{I}$는 참조 모델과 동일하다.

\[\begin{equation} \Psi : \mathcal{I} \times \mathcal{Y}^n \rightarrow \mathcal{I} \end{equation}\]

또한 영역 선택 맵은 $F_i(I) = I$로 정의되고 픽셀 가중치는 마스크에 따라 $W_i = M_i$로 설정되며 $\Psi$ step은 최소 제곱 문제의 해로 정의된다.

\[\begin{equation} \Psi (J_t, z) = \underset{J \in \mathcal{I}}{\arg \min} \sum_{i=1}^n \| M_i \otimes [J - \Phi (J_t \vert y_i)] \|^2 \end{equation}\]

이 LS 문제에 대한 해는 수치적으로 계산된다. 각 step에서 주어진 각 프롬프트에 대해 사전 학습된 diffusion model을 적용하며, 결과로 여러 diffusion 방향 $\Phi (J_t \vert y_i)$가 나온다. $J_t$의 각 픽셀이 이를 포함하는 영역 $M_i$와 관련된 평균 방향을 따르도록 권장한다.

Fidelity to tight masks

사용자가 타이트한 마스크를 제공하는 경우 타이트한 마스크에 대한 높은 충실도를 얻는 것이 가능하다. 저자들은 diffusion process에서 레이아웃이 초기에 결정된다는 점을 인지하고, 원하는 레이아웃을 일치시키기 위해 $\Phi (J_t \vert y_i)$가 프로세스 초기에 $M_i$ 영역에 집중하도록 유도하고, 조화로운 결과를 얻기 위해 다음 이미지의 전체 컨텍스트를 살펴보았다. 저자들은 $F_i$ 맵에 시간 의존성을 통합하여 부트스트래핑 단계를 도입하였다.

\[\begin{equation} F_i (J, t) = \begin{cases} J_t & \quad \textrm{if} \; t \le T_\textrm{init} \\ M_i \otimes J_t + (1 - M_i) \otimes S_t & \quad \textrm{otherwise} \end{cases} \end{equation}\]

여기서 $T_\textrm{init}$은 부트스트래핑 중지 단계를 나타내는 파라미터이고 $S_t$는 배경으로 사용되는 일정한 색상을 갖는 랜덤 이미지이다.

Results

모든 실험에서 Stable Diffusion을 사용하였다. 사용된 Stable Diffusion은 diffusion process가 latent space $\mathcal{I} \in \mathbb{R}^{64 \times 64 \times 4}$에서 정의되었고 디코더가 $[0, 1]^{512 \times 512 \times 3}$로 이미지를 복구하도록 학습되었다. 이와 비슷하게 MultiDiffusion 프로세스에서 $\Psi$는 latent space $\mathcal{J} \in \mathbb{R}^{H^\prime \times W^\prime \times 4}$에서 정의되었고 디코더는 타겟 이미지 공간 $[0, 1]^{8H^\prime \times 8W^\prime \times 3}$의 이미지를 생성한다.

1. Panorama Generation

다음은 Blended Latent Diffusion (BLD), Stable Inpainting (SI)과 text-to-paranoma 결과를 비교한 것이다.

다음은 파라노마 생성에 대한 정량적 비교 결과이다.

2. Region-based Text-to-Image Generation

다음은 주어진 대략적인 장면 레이아웃 guidance (왼쪽)에 대하여 MultiDiffusion이 생성한 다양한 샘플들이다.

다음은 다양한 레이아웃에 대하여 생성된 샘플들이다.

다음은 영역 기반 text-to-image 생성 결과를 비교한 것이다.

다음은 부트스트래핑에 대한 ablation 결과이다.

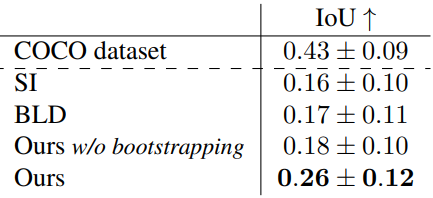
다음은 COCO 데이터셋에서 영역 기반 생성 결과를 비교한 표이다.

Limitations

본 논문의 방법은 참조 diffusion model의 generative prior에 크게 의존한다. 즉, 결과의 품질은 모델이 제공하는 diffusion 경로에 따라 달라진다. 따라서 참조 모델이 “나쁜” 경로를 선택하면 (ex. 나쁜 시드, 편향된 텍스트 프롬프트) 결과도 영향을 받는다. 어떤 경우에는 프레임워크에 더 많은 제약 조건을 도입하거나 프롬프트 엔지니어링을 적용하여 이를 완화할 수 있다.