[논문리뷰] Human Motion Diffusion Model

ICLR 2023. [Paper] [Page] [Github]
Guy Tevet, Sigal Raab, Brian Gordon, Yonatan Shafir, Daniel Cohen-Or, Amit H. Bermano
Tel Aviv University
29 Sep 2022

Introduction

인간 모션 생성은 가능한 모션의 범위가 넓고 고품질 데이터를 수집하는 데 드는 어려움과 비용을 포함하여 여러 가지 이유로 어려운 분야이다. 모션이 자연어에서 생성되는 최근 등장한 text-to-motion 설정의 경우 또 다른 고유한 문제는 데이터 라벨링이다. 예를 들어, “kick”이라는 레이블은 가라테 킥뿐만 아니라 축구 킥을 의미할 수 있다. 동시에 특정 킥이 주어지면 이를 수행하는 방법에서 전달하는 감정에 이르기까지 다대다 문제를 구성하는 여러 가지 방법이 있다. 현재 접근 방식은 텍스트에서 모션으로 그럴듯한 매핑을 보여준다. 그러나 이러한 모든 접근 방식은 주로 오토인코더 또는 VAE를 사용하기 때문에 학습된 분포를 여전히 제한한다. 이러한 측면에서 diffusion model은 타겟 분포에 대한 가정이 없고 다대다 분포 일치 문제를 잘 표현하는 것으로 알려져 있기 때문에 인간 모션 생성에 더 적합한 후보이다.

Diffusion model은 컴퓨터 비전과 그래픽 커뮤니티에서 상당한 주목을 받고 있는 생성적 접근 방식이다. 조건부 생성을 위해 학습되었을 때 최근 diffusion model은 이미지 품질과 semantic 측면에서 획기적인 발전을 보여주었다. Diffusion model의 역량은 동영상과 3D 포인트 클라우드를 포함한 다른 영역에서도 나타났다. 그러나 diffusion model의 문제점은 리소스를 많이 요구하고 제어하기 어렵다는 점이다.

본 논문에서는 인간 모션 도메인에 대해 신중하게 조정된 diffusion 기반 생성 모델인 Motion Diffusion Model (MDM)을 소개한다. Diffusion 기반인 MDM은 앞서 언급한 도메인의 기본 다대다 표현으로부터 이득을 얻으며, 이는 결과 모션 품질과 다양성에서 알 수 있다. 또한 MDM은 모션 생성 도메인에서 이미 잘 확립된 통찰력을 결합하여 훨씬 더 가볍고 제어할 수 있도록 한다.

첫째, MDM은 일반적으로 사용하는 U-net backbone 대신에 transformer 기반이다. 아키텍처는 가볍고 모션 데이터 (조인트 모음)의 시간적 및 비공간적 특성에 더 잘 맞는다. 많은 양의 모션 생성 연구가 기하학적 loss를 사용한 학습에 전념하고 있다. 예를 들어 일부 연구들은 jitter를 방지하기 위해 모션의 속도를 조절하거나 전용 항을 사용하여 특히 발 미끄러짐을 고려한다. 이러한 연구들과 일관되게 diffusion 설정에서 기하학적 loss를 적용하면 생성이 향상된다.

MDM 프레임워크에는 다양한 형태의 컨디셔닝을 가능하게 하는 일반 디자인이 있다. 본 논문은 text-to-motion, action-to-motion, unconditional 생성의 세 가지 task를 선보인다. Classifier-free 방식으로 모델을 학습하여 다양성과 충실도를 절충하고 동일한 모델에서 조건부 및 unconditional 샘플링을 수행할 수 있다. Text-to-motion task에서 모델은 HumanML3D와 KIT 벤치마크에서 SOTA 결과를 달성하는 일관된 모션을 생성한다. 또한 user study에 따르면 42%의 시간 동안 실제 모션보다 생성된 모션을 선호한다. Action-to-motion에서 MDM은 HumanAct12와 UESTC 벤치마크에서 이 task를 위해 특별히 설계되었지만 SOTA를 능가한다.

마지막으로 저자들은 완성과 편집의 시연도 하였다. Diffusion 이미지 인페인팅을 적용하여 모션 prefix와 suffix를 설정하고 모델을 사용하여 간격을 채운다. 텍스트 조건에서 그렇게 하면 MDM이 원래 입력의 의미를 여전히 유지하는 특정 모션으로 간격을 채우도록 가이드한다. 시간적으로가 아니라 joint space에서 인페인팅을 수행함으로써 다른 부분을 변경하지 않고 특정 신체 부분의 semantic 편집을 시연하였다.

Motion Diffusion Model

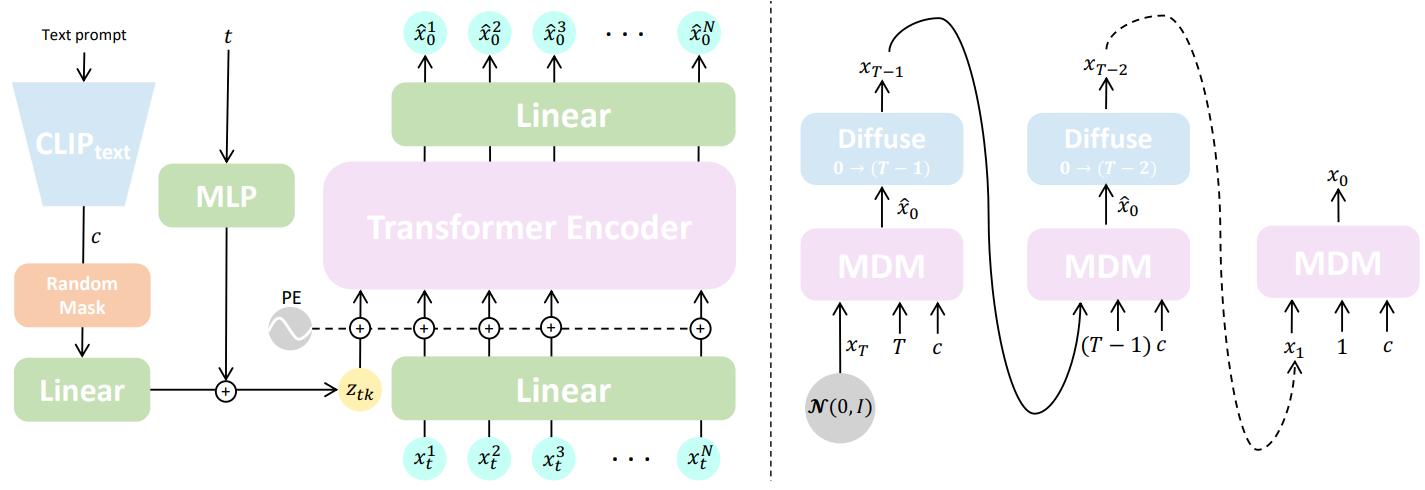
본 논문의 방법의 개요는 위 그림에 설명되어 있다. 주어진 임의의 조건 $c$에서 길이 $N$의 인간 모션 $x^{1:N}$을 합성하는 것이 목표이다. 이 조건은 오디오, 자연어 (text-to-motion), discrete한 클래스 (action-to-motion)와 같이 합성을 지시하는 실제 신호일 수 있다. 또한 unconditional한 모션 생성도 가능하며 이를 null 조건 $c = \emptyset$로 표시한다. 생성된 모션 \(x^{1:N} = \{x^i\}_{i=1}^N\)은 관절 회전 또는 위치 $x^i \in \mathbb{R}^{J \times D}$로 표현되는 일련의 인간 포즈이며, 여기서 $J$는 관절 수이고 $D$는 관절 표현의 차원이다. MDM은 위치, 회전 또는 둘 다로 표시되는 모션을 허용할 수 있다.

Framework

Diffusion은 Markov noising process \(\{x_t^{1:N}\}_{t=0}^T\)으로 모델링되며, 여기서 $x_0^{1:N}$은 데이터 분포에서 도출되고

\[\begin{equation} q(x_t^{1:N} \vert x_{t-1}^{1:N}) = \mathcal{N} (\sqrt{\alpha_t} x_{t-1}^{1:N}, (1 - \alpha_t) I) \end{equation}\]

이다. 여기서 $\alpha_t \in (0, 1)$은 hyperparameter이다. $\alpha_t$가 충분히 작으면 \(x_T^{1:N} \sim \mathcal{N}(0, I)\)로 근사할 수 있다. 여기에서 noising step $t$에서 전체 시퀀스를 나타내기 위해 $x_t$로 표기한다.

컨디셔닝된 모션 합성은 분포 $p(x_0 \vert c)$를 점진적으로 깨끗하게 만드는 $x_T$의 reverse diffusion process로 모델링한다. DDPM에서와 같이 $\epsilon_t$를 예측하는 대신, unCLIP을 따라 다음과 같은 간단한 목적 함수를 사용하여 신호 자체, 즉 \(\hat{x}_0 = G(x_t, t, c)\)를 예측한다.

\[\begin{equation} \mathcal{L}_\textrm{simple} = \mathbb{E}_{x_0 \sim q(x_0 \vert c), t \sim [1,T]} [\| x_0 - G (x_t, t, c) \|_2^2] \end{equation}\]

Geometric losses

모션 도메인에서 생성 네트워크는 기하학적 loss들을 사용하여 표준으로 정규화된다. 이러한 loss들은 물리적 속성을 적용하고 아티팩트를 방지하여 자연스럽고 일관된 모션을 장려한다. 본 논문에서는

1. 위치 (회전을 예측하는 경우)
2. 발 접촉
3. 속도

를 조절하는 세 가지 일반적인 기하학적 loss들을 실험하였다.

\[\begin{equation} \mathcal{L}_\textrm{pos} = \frac{1}{N} \sum_{i=1}^N \| \textrm{FK} (x_0^i) - \textrm{FK} (\hat{x}_0^i) \|_2^2 \\ \mathcal{L}_\textrm{foot} = \frac{1}{N-1} \sum_{i=1}^{N-1} \| (\textrm{FK} (\hat{x}_0^{i+1}) - \textrm{FK} (\hat{x}_0^i)) \cdot f_i \|_2^2 \\ \mathcal{L}_\textrm{vel} = \frac{1}{N-1} \sum_{i=1}^{N-1} \| (x_0^{i+1} - x_0^i) - (\hat{x}_0^{i+1} - \hat{x}_0^i) \|_2^2 \end{equation}\]

관절 회전을 예측하는 경우 $\textrm{FK}(\cdot)$는 관절 회전을 관절 위치로 변환하는 forward kinematic 함수를 나타낸다. 관절 회전을 예측하지 않는 경우 항등 함수를 나타낸다. \(f_i \in \{0, 1\}^J\)는 각 프레임 $i$에 대한 발 접촉 이진 마스크이다. 발에만 해당되며 땅에 닿았는지 여부를 나타내고 이진 ground-truth 데이터에 따라 설정된다. 본질적으로 지면에 닿았을 때 속도를 무효화하여 발이 미끄러지는 효과를 완화한다.

전체적으로 학습 loss는 다음과 같다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{simple} + \lambda_\textrm{pos} \mathcal{L}_\textrm{pos} + \lambda_\textrm{vel} \mathcal{L}_\textrm{vel} + \lambda_\textrm{foot} \mathcal{L}_\textrm{foot} \end{equation}\]

Model

간단한 transformer 인코더 아키텍처로 $G$를 구현한다. Transformer 아키텍처는 시간적으로 인식되어 임의 길이 모션을 학습할 수 있으며 모션 도메인에 대해 잘 입증되었다. Denoising step $t$와 조건 코드 $c$는 각각 별도의 feed-forward network에 의해 transformer 차원으로 project된 다음 합산되어 토큰 $z_{tk}$를 생성한다. Noisy한 입력 $x_t$의 각 프레임은 transformer 차원으로 선형적으로 project되고 표준 위치 임베딩과 합산된다. $z_{tk}$와 project된 프레임은 인코더에 공급된다. 첫 번째 출력 토큰을 제외하고 인코더 결과는 원래 모션 차원으로 다시 project되며 예측 \(\hat{x}_0\)로 사용된다. CLIP 텍스트 인코더를 사용하여 텍스트 프롬프트를 $c$로 인코딩하여 text-to-motion을 구현하고 클래스별로 학습된 임베딩을 사용하여 action-to-motion을 구현한다.

Sampling

$p(x_0 \vert c)$에서의 샘플링은 DDPM에 따라 반복적인 방식으로 수행된다. 모든 timestep $t$에서 깨끗한 샘플 \(\hat{x}_0 = G(x_t, t, c)\)를 예측하고 다시 $x_{t−1}$로 noise 처리한다. 이것은 $x_0$가 될 때까지 $t = T$에서 반복된다. Classifier-free guidance를 사용하여 모델 $G$를 학습한다. 실제로 $G$는 $G(x_t, t, \emptyset)$가 $p(x_0)$에 가까워지도록 샘플의 10%에 대해 $c = \emptyset$를 임의로 설정하여 조건부 분포와 unconditional 분포를 모두 학습한다. 그런 다음 $G$를 샘플링할 때 $s$를 사용하여 두 변형을 보간하거나 외삽하여 다양성과 충실도를 절충할 수 있다.

\[\begin{equation} G_s (x_t, t, c) = G (x_t, t, \emptyset) + s \cdot (G (x_t, t, c) - G (x_t, t, \emptyset)) \end{equation}\]

Editing

모션 데이터에 diffusion 인페인팅을 적용하여 시간 도메인에서 모션 중간, 공간 도메인에서 신체 부분 편집을 가능하게 한다. 편집은 학습 없이 샘플링 중에만 수행된다. 모션 시퀀스 입력의 부분 집합이 주어지면 모델을 샘플링할 때 각 iteration에서 모션의 입력 부분으로 \(\hat{x}_0\)를 덮어쓴다. 이렇게 하면 누락된 부분을 완성하면서 생성이 원래 입력과 일관성을 유지하도록 한다. 시간적 설정에서는 모션 시퀀스의 prefix 프레임과 suffix 프레임이 입력되어 모션 중간 문제를 해결한다. 편집은 조건부 또는 unconditional ($c = \emptyset$)로 수행할 수 있다. 공간적 설정에서 동일한 완성 기법을 사용하여 나머지 부분은 그대로 유지하면서 조건 $c$에 따라 신체 부분을 다시 합성할 수 있다.

Experiments

1. Text-to-Motion

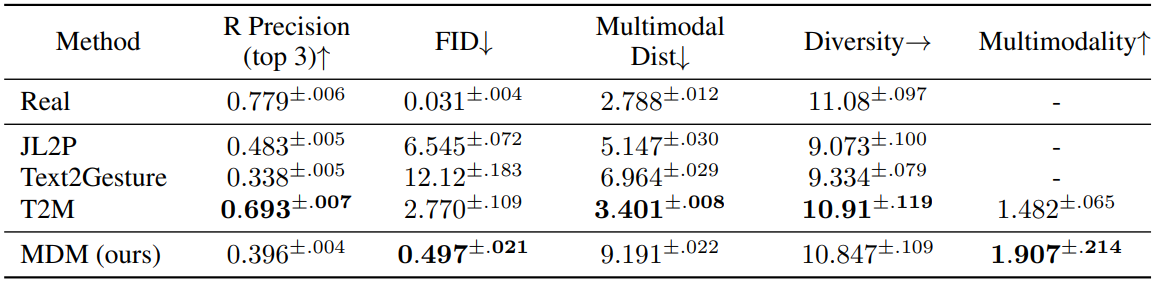
다음은 HumanML3D test set에서 정량적으로 평가한 표이다.

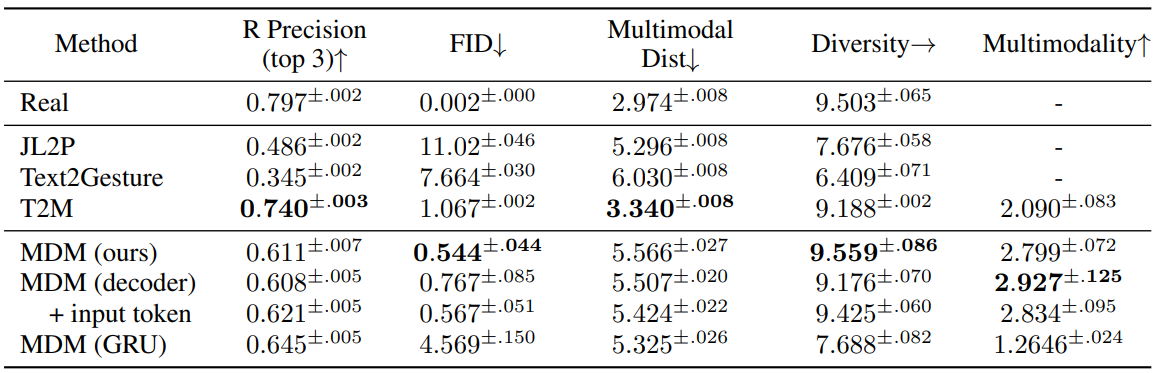
다음은 KIT test set에서 정량적으로 평가한 표이다.

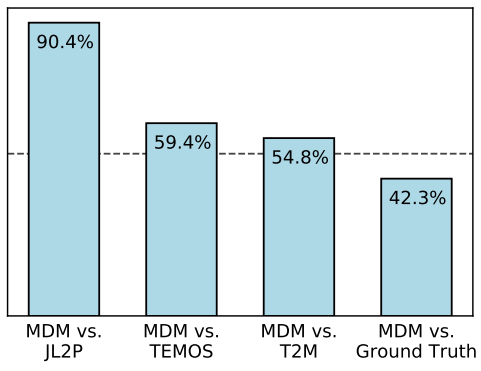
다음은 KIT에 대한 user study 결과이다.

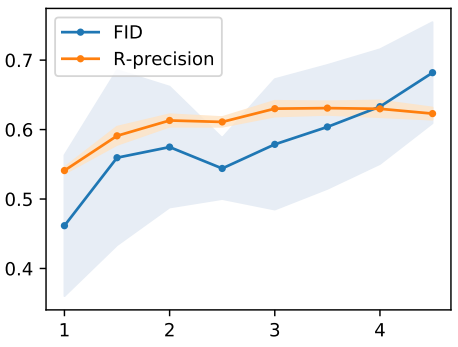
다음은 HumanML3D에서 guidance scale $s$에 따른 FID와 R-precision을 나타낸 그래프이다.

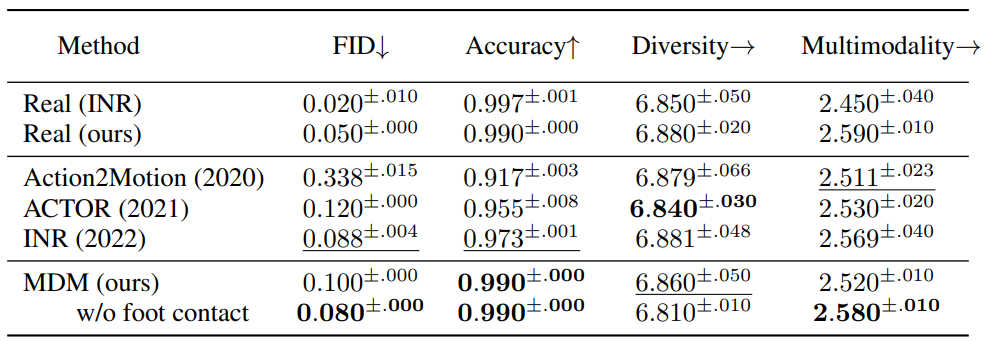
2. Action-to-Motion

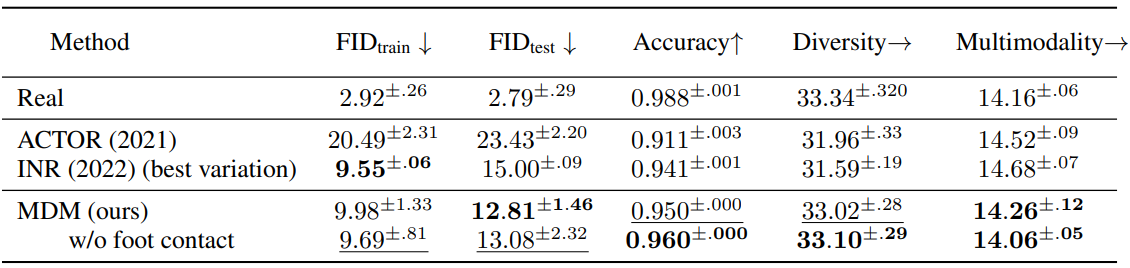
다음은 HumanAct12에서 정량적으로 action-to-motion을 평가한 표이다.

다음은 UESTC에서 정량적으로 action-to-motion을 평가한 표이다.

Additional Applications

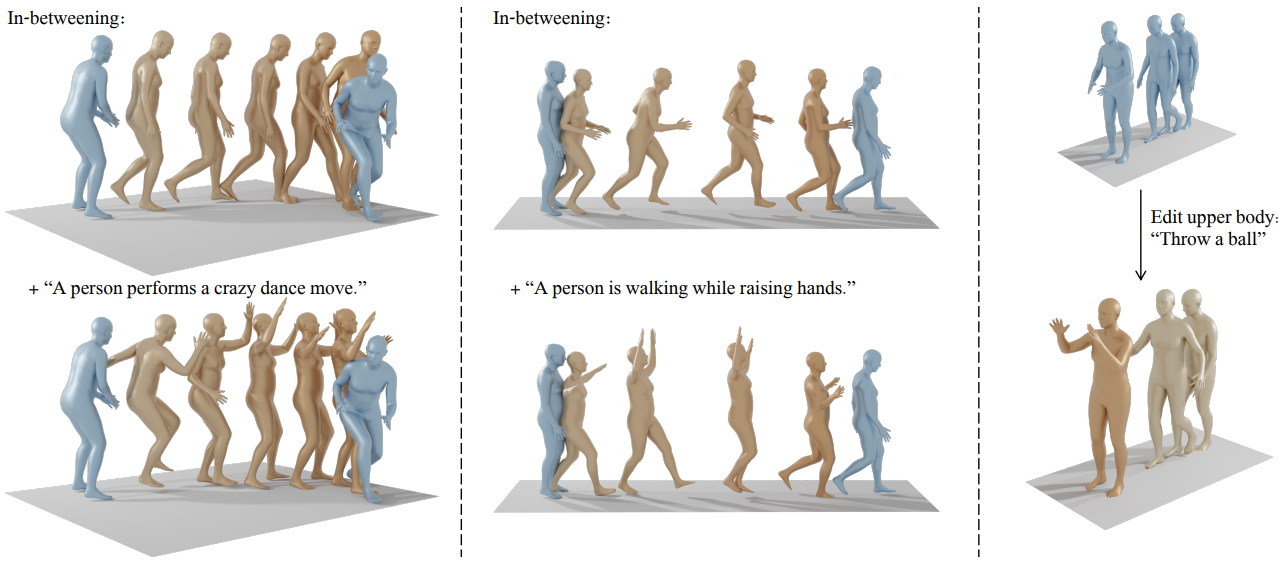
1. Motion Editing

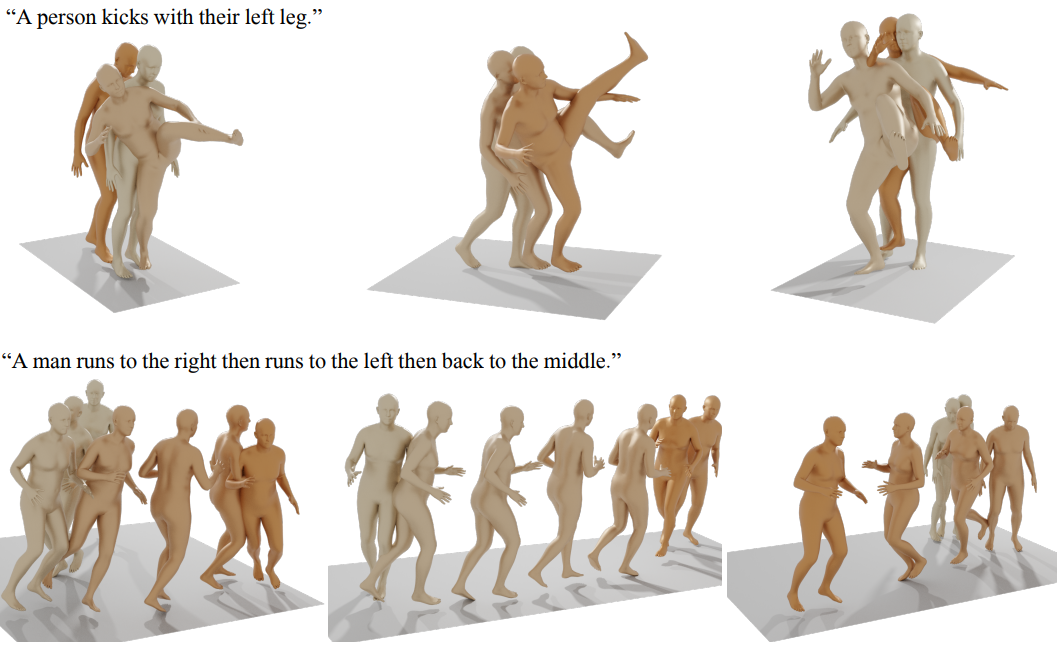
다음은 모션 편집의 예시이다. 하늘색 프레임은 모션 입력을 나타내고 갈색 프레임은 생성된 모션을 나타낸다.

2. Unconstrained Synthesis

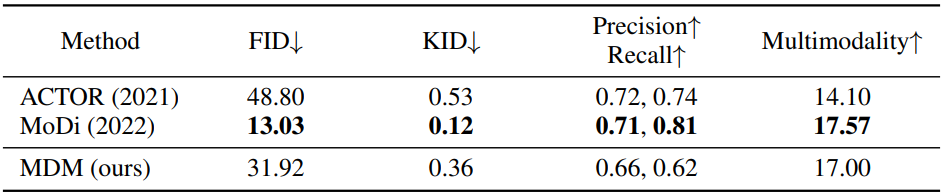
다음은 HumanAct12에서 정량적으로 제약 없는 합성을 평가한 표이다.