[논문리뷰] Mixture-of-Recursions: Learning Dynamic Recursive Depths for Adaptive Token-Level Computation
arXiv 2025. [Paper] [Github]
Sangmin Bae, Yujin Kim, Reza Bayat, Sungnyun Kim, Jiyoun Ha, Tal Schuster, Adam Fisch, Hrayr Harutyunyan, Ziwei Ji, Aaron Courville, Se-Young Yun
KAIST AI | Mila | Google Cloud | Google DeepMind | Google Research | Université de Montréal
14 Jul 2025
Introduction
Transformer 네트워크를 수천억 개의 파라미터로 scaling함으로써 인상적인 few-shot 일반화와 추론이 가능해졌지만, 이에 따른 메모리 사용량과 연산 요구량으로 인해 학습 및 배포가 어려워졌다. 이러한 어려움으로 인해 연구자들은 효율적인 디자인을 모색하게 되었다. 그 중, 파라미터 효율성 (모델 가중치를 줄이거나 공유하는 방식)과 적응형 연산 (필요할 때만 더 많은 연산을 사용하는 방식)은 활발하게 연구되고 있는 연구 방향이다.
파라미터 효율성을 높이는 검증된 방법 중 하나는 공유 가중치 세트를 여러 레이어에서 재사용하는 layer tying이다. 적응형 연산의 경우, 일반적인 접근 방식은 조기 종료로, 더 간단한 토큰을 예측할 때 네트워크에서 더 일찍 종료하여 계산을 동적으로 할당한다. 각각에서 달성된 진전에도 불구하고 파라미터 효율성과 적응형 연산을 효과적으로 통합하는 아키텍처는 여전히 부족하다.
동일한 공유 레이어들을 여러 번 반복적으로 적용하는 모델인 Recursive Transformer는 내장된 가중치 공유로 인해 강력한 기반을 제공한다. 그러나 동적 재귀에 대한 이전 방법들은 추가적인 학습 절차가 필요하거나 효율적인 배포에 어려움을 겪는 등 실질적인 장애물로 인해 종종 제한되었다. 이로 인해 대부분의 방법들은 여전히 더 간단한 고정 깊이 재귀를 기본으로 사용하는데, 이는 모든 토큰에 동일한 양의 계산을 적용하므로 진정한 토큰 수준의 적응형 연산 할당을 제공할 수 없다.
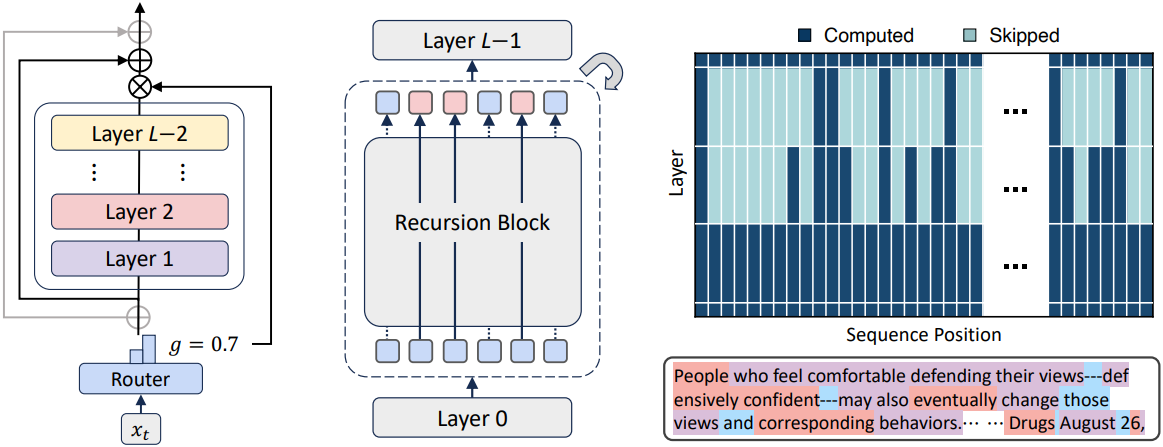
본 연구에서는 Recursive Transformer의 잠재력을 최대한 활용하는 통합 프레임워크인 Mixture-of-Recursions (MoR)를 소개한다. MoR은 가벼운 라우터를 end-to-end 방식으로 학습시켜 토큰별 재귀 깊이를 할당한다. 즉, 각 토큰에 필요한 사고의 깊이에 따라 공유 파라미터 블록을 적용하는 횟수를 결정하여 연산이 가장 필요한 곳에 집중한다. 이러한 동적인 토큰 수준의 재귀는 재귀 기반 KV 캐싱을 본질적으로 용이하게 하여 각 토큰에 할당된 재귀 깊이에 해당하는 key-value 쌍을 선택적으로 저장하고 검색한다. 이러한 캐싱 전략은 메모리 트래픽을 줄여 사후 수정에 의존하지 않고도 처리량을 향상시킨다. 따라서 MoR은 단일 아키텍처 내에서 가중치를 연결하여 파라미터를 줄이고, 토큰을 라우팅하여 중복 연산을 줄이고, key-value를 재귀적으로 캐싱하여 메모리 트래픽을 줄인다.
개념적으로 MoR은 latent space 추론을 위한 사전 학습 프레임워크를 제공한다. 즉, 하나의 파라미터 블록을 반복적으로 적용하여 비언어적 사고를 수행하며, 각 토큰의 디코딩 과정에서 이러한 latent 사고를 직접 활성화한다. 또한, 라우팅 메커니즘은 적응적 추론을 용이하게 하며, 기존 연구들의 고정된 사고 깊이를 넘어섰다. 본질적으로, MoR은 모델이 토큰별로 사고 깊이를 효율적으로 조정하여 파라미터 효율성과 적응적 계산을 통합할 수 있도록 한다.
Method
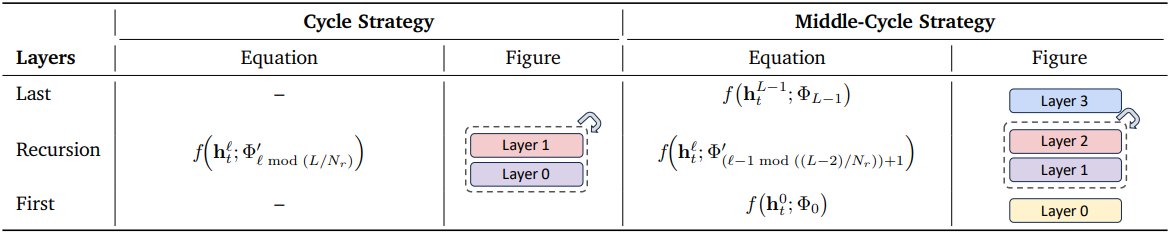
Recursive Transformer는 4가지 파라미터 공유 전략, Cycle, Sequence, Middle-Cycle, Middle-Sequence를 사용할 수 있다. 예를 들어, 레이어가 9개이고 $N_r = 3$번 재귀를 하는 경우, Cycle은 [(0, 1, 2), (0, 1, 2), (0, 1, 2)]로, Sequence는 [(0, 0, 0), (1, 1, 1), (2, 2, 2)]로 재귀를 한다. Middle은 첫 번째 레이어와 마지막 레이어를 공유하지 않는다.
모델 파라미터는 연결되어 있지만, 일반적으로 각 깊이에 대해 별도의 KV 캐시가 사용되므로 캐시 크기를 줄이지 못한다. 또한, 대부분의 기존 재귀 모델은 다양한 복잡성을 무시하고 모든 토큰에 고정된 재귀 깊이를 적용한다. 이상적으로는 재귀 깊이가 사전 학습 과정에서 동적으로 학습되어 모델이 데이터 기반 방식으로 각 토큰의 난이도에 맞춰 계산 경로를 조정할 수 있어야 한다. 그러나 이러한 동적 경로를 사용할 경우 종료된 토큰은 후속 재귀 깊이에서 KV 쌍이 누락될 수 있다.
MoR의 핵심은 두 가지 구성 요소로 구성된다.
- 라우팅 메커니즘: 토큰별 재귀 단계를 할당하여 더 어려운 토큰에 계산을 적응적으로 집중시킨다.
- KV 캐싱 전략: 각 재귀 단계에서 KV 쌍을 저장하고 선택적으로 활용한다.
1. Routing Strategies: Expert-choice vs. Token-choice
Expert-choice routing
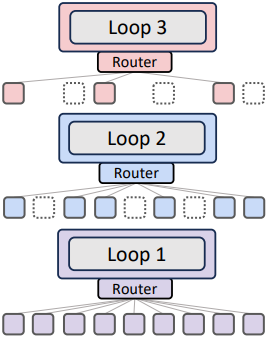
MoD 모델의 top-k gating에서 영감을 받은 expert-choice routing에서 각 재귀 깊이는 expert가 되어 선호하는 상위 $k$개의 토큰을 선택한다. 예를 들어, expert가 3명인 경우 ($N_r = 3$), expert 1은 첫 번째 재귀 단계를 적용하고, expert 2는 두 번째 재귀 단계를 적용하는 방식이다. 각 재귀 단계 $r$에서 해당 라우터는 hidden state \(\mathcal{H}_t^r\) ($r$번째 재귀 블록의 입력)와 라우팅 파라미터 \(\theta_r\)을 사용하여 토큰 $t$에 대한 스칼라 점수 $g_t^r$을 계산한다.
($\mathcal{G}$는 sigmoid나 tanh와 같은 activation function)
그러면 상위 $k$개의 토큰이 재귀 블록을 통과하도록 선택된다.
\[\begin{equation} \mathcal{H}_t^{r+1} = \begin{cases} g_t^r f (\mathcal{H}_t^r, \Phi^\prime) + \mathcal{H}_t^r & \textrm{if } g_t^r > P_\beta (G^r) \\ \mathcal{H}_t^r & \textrm{otherwise} \end{cases} \end{equation}\](\(P_\beta (G^r)\)은 재귀 단계 $r$에서 모든 점수에 대한 $\beta$-percentile threshold)
단계적으로 일관된 진행을 보장하기 위해 계층적 필터링을 채택했다. 재귀 단계 $r$에서 선택된 토큰만 $r+1$에서 재평가될 수 있다. 이는 처음부터 학습하면서 조기 종료 동작을 시뮬레이션한다. 더 깊은 레이어는 점점 더 추상적이고 sparse한 정보를 인코딩하는 경향이 있으므로, 이 메커니즘은 가장 까다로운 토큰에 대해서만 계산을 우선시한다.
Token-choice routing
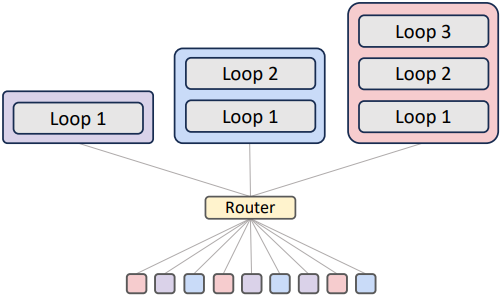
각 재귀 단계마다 토큰을 선택하는 expert-choice와 달리, token-choice는 각 토큰을 처음부터 전체 재귀 블록 시퀀스에 할당한다. Hidden state \(\mathcal{H}_t^1\)가 주어지면 라우터는 expert에 대한 non-linear function (softmax 또는 sigmoid)을 계산한다.
($g_t^j$는 expert $j$에 대한 라우팅 점수)
토큰은 expert \(i = \textrm{argmax}_j g_t^j\)에 할당되며, 이는 재귀를 $i$번 순차적으로 적용하는 것과 같다. 그러면 hidden state는 다음과 같이 재귀적으로 업데이트된다.
\[\begin{equation} \mathcal{H}_t^{r+1} = \begin{cases} g_t^r f (\mathcal{H}_t^r, \Phi^\prime) + \mathcal{H}_t^1 & \textrm{if } r = i \\ g_t^r f (\mathcal{H}_t^r, \Phi^\prime) & \textrm{otherwise} \end{cases} \end{equation}\]강점과 한계점
Expert-choice routing은 정적인 top-k 선택으로 완벽한 부하 분산을 보장하지만, 정보 누출이라는 문제점을 안고 있다. 학습 중 이러한 인과관계 위반은 보조 라우터 또는 regularization loss을 악용하여 inference 시점에 상위 $k$개의 토큰을 미래 토큰 정보에 접근하지 않고 정확하게 감지하도록 한다. 한편, token-choice routing은 이러한 누출이 없지만, 고유한 부하 분산 문제로 인해 일반적으로 balancing loss 또는 loss-free 알고리즘이 필요하다.
2. KV Caching Strategies: Recursion-wise Caching vs. Recursive Sharing
동적 깊이 모델은 autoregressive 디코딩 중 KV 캐시 일관성 문제로 어려움을 겪는 경우가 많다. 토큰이 조기에 종료되는 경우, 후속 토큰에 중요한 정보가 될 수 있는 더 깊은 레이어의 해당 key와 value가 누락된다. 본 논문은 MoR 모델에 맞춘 두 가지 KV 캐시 전략을 탐구하였다.
Recursion-wise KV caching
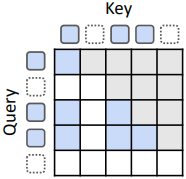
Recursion-wise caching은 특정 재귀 단계로 라우팅된 토큰만 해당 레벨에 key-value 항목을 저장한다. 따라서 각 재귀 깊이에서의 KV 캐시 크기는 expert-choice의 경우 $k$에 의해, token-choice의 경우 실제 균형 비율에 따라 결정된다. 따라서 attention은 로컬하게 캐싱된 토큰으로 제한된다. 이 디자인은 블록 로컬 계산을 촉진하여 메모리 효율성을 향상시키고 IO 요구량을 줄인다.
Recursive KV sharing
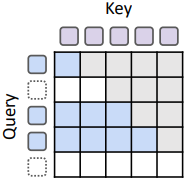
MoR 모델의 핵심 디자인 선택은 모든 토큰이 최소한 첫 번째 재귀 블록을 통과한다는 것이다. Recursive sharing은 이 초기 단계에서 KV 쌍만 캐싱하고 이후 모든 재귀에서 재사용한다. 따라서 선택 용량에 따라 각 재귀 깊이에서 query 길이가 짧아질 수 있지만, key와 value 길이는 전체 시퀀스를 일관되게 유지한다. 이를 통해 모든 토큰은 재계산 없이 이전 컨텍스트에 접근할 수 있다.
강점과 한계점
Recursion-wise caching은 전체 모델에서 KV 메모리와 IO를 약 $(N_r + 1)/2N_r$배로 줄인다. 또한 레이어당 attention FLOPs를 $(k / N_\textrm{ctx})^2$배로 줄여 학습 및 inference 모두에서 효율성을 크게 향상시킨다.
Recursive sharing은 컨텍스트를 글로벌하게 재사용하여 메모리를 $1/N_r$배로 최대한 줄인다. 특히, 공유된 깊이에서 KV projection 및 prefill 연산을 건너뛰면 상당한 속도 향상을 얻을 수 있다. 그러나 attention FLOPs는 $k / N_\textrm{ctx}$배로만 감소하며, IO는 줄지 않기 때문에 IO가 양이 많으면 여전히 디코딩 병목 현상이 발생한다.
Experiments
1. Main Results
다음은 고정된 FLOPs(16.5e18)와 토큰 수(20B)에 대하여 Transformer, Recursive Transformer, MoR을 비교한 결과이다.
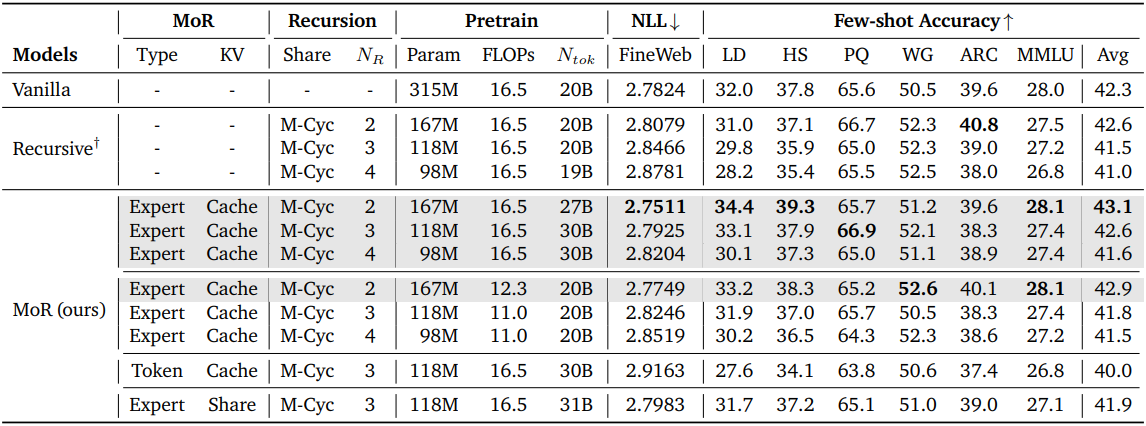
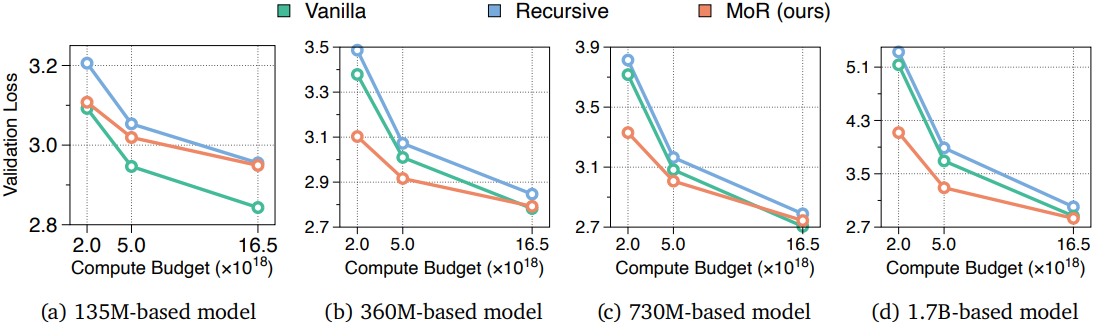
다음은 다양한 연산량 예산과 모델 크기에 대한 validation loss를 비교한 결과이다. (MoR 모델은 expert-choice routing과 recursion-wise caching을 사용)
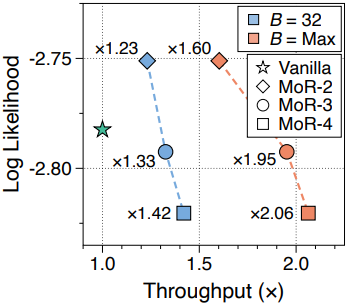
다음은 inference 처리량을 비교한 결과이다.
2. Ablation Studies
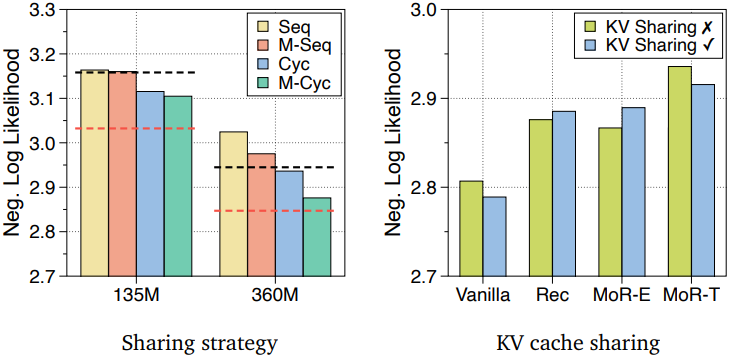
다음은 (왼쪽) Recursive Transformer의 파라미터 공유 전략과 (오른쪽) KV 캐싱 전략에 대한 ablation 결과이다.
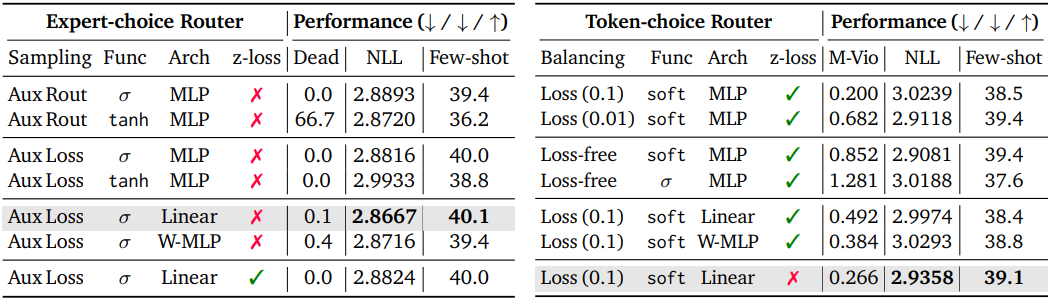
다음은 라우팅 전략에 대한 ablation 결과이다.
3. Analysis
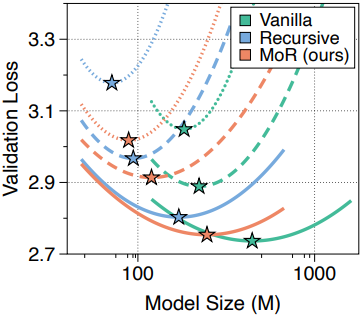
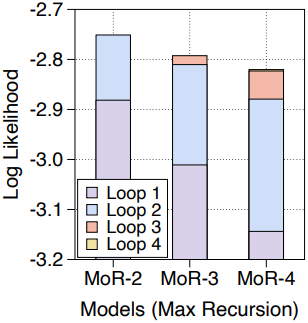
다음은 (왼쪽) compute-optimal scaling 분석 결과와 (오른쪽) \(N_r = \{2, 3, 4\}\)인 MoR 모델에 대한 test-time scaling 분석 결과이다.
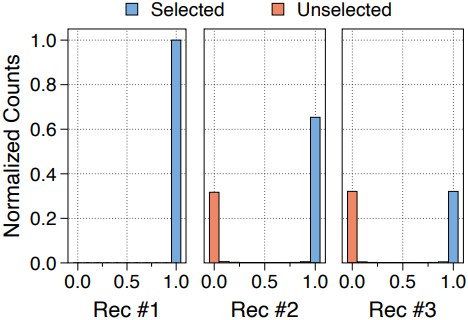
다음은 360M MoR 모델의 학습된 라우터 점수의 예시이다. ($N_r = 3$, expert-choice routing, recursion-wise caching)