Diffusion은 신이고 GPT는 무적이다

NeurIPS 2025. [Paper] [Page] [Github]
Ruicheng Wang, Sicheng Xu, Cassie Dai, Jianfeng Xiang, Yu Deng, Xin Tong, Jiaolong Yang
USTC | Microsoft Research | Tsinghua University
3 Jul 2025

MoGe의 후속 논문

Introduction

MoGe는 단일 이미지로부터 affine-invariant point map을 예측하고 SOTA geometry 정확도를 달성하였다. 본 논문은 metric geometry 예측 능력을 도입하고 geometry 세분성을 개선하여 복잡한 디테일을 포착함으로써 MoGe를 확장하였다.

Metric geometry 추정의 경우, 간단한 해결책은 metric space에서 절대적인 point map을 직접 예측하는 것이지만, 초점 거리 모호성 문제가 존재한다. 이를 해결하기 위해, 저자들은 두 가지 간단하고 직관적이면서도 효과적인 대안을 살펴보았다.

  1. Metric scale을 point map 예측에 직접 통합하는 shift-invariant point map 표현을 사용
  2. Affine-invariant 표현을 유지하면서 분리된 방식으로 글로벌 metric scale을 추가로 예측

두 방법 모두 초점 거리 모호성을 완화하지만, 후자가 더 정확한 결과를 제공하는데, 이는 relative geometry를 더 잘 보존하는 잘 정규화된 point map 공간 덕분일 가능성이 높다.

저자들은 실제 학습 데이터에 대한 선명한 깊이 레이블을 생성하기 위한 실용적인 데이터 정제 접근법을 제안하였다. 실제 데이터 레이블은 종종 노이즈가 많고 불완전하며, 특히 물체 경계 부분에서 더욱 그렇다. 이는 미세한 geometry 학습을 방해한다. Depth Anything V2와 같은 이전 연구들은 합성 데이터 레이블만 사용하여 2D 시각화에서는 선명하지만 geometry 정확도는 떨어진다. 마찬가지로 Depth Pro는 두 단계 중 두 번째 단계에서는 합성 데이터만 사용한다.

이와는 대조적으로, 본 논문에서는 높은 geometry 정확도를 보장하기 위해 학습 과정 전반에 걸쳐 실제 데이터를 활용한다. 파이프라인은 실제 데이터에서 주로 물체 경계 주변에서 발견되는 불일치하거나 잘못된 깊이 값을 필터링한 후, 합성 데이터로 학습된 모델을 사용하여 깊이 인페인팅을 통해 누락된 영역을 채운다. 이 접근법은 훨씬 더 미세한 디테일을 제공하며, geometry 정확도는 처리되지 않은 전체 실제 데이터로 학습된 모델과 유사하다.

Method


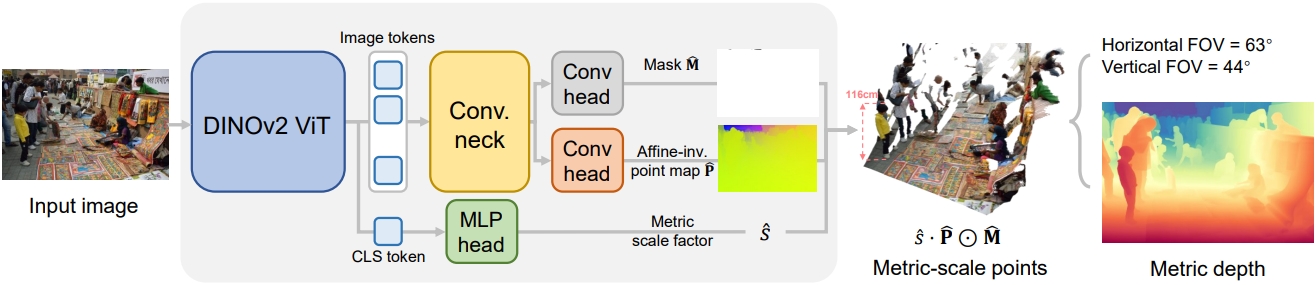
본 논문의 방법은 단일 이미지를 처리하여 장면의 3D point map을 예측함으로써 정확한 relative geometry, metric scale, 그리고 세밀한 디테일을 구현한다. 이 방법은 affine-invariant point map 재구성에 중점을 둔 MoGe를 기반으로 한다. 본 논문에서는 정확한 metric geometry 추정으로 확장하기 위한 효과적인 전략들을 모색하였다. 또한, 실제 학습 데이터를 최대한 활용하여 정밀하고 상세한 geometry 재구성을 동시에 달성하는 데이터 정제 방법을 개발하였다.

1. Metric Scale Geometry Estimation


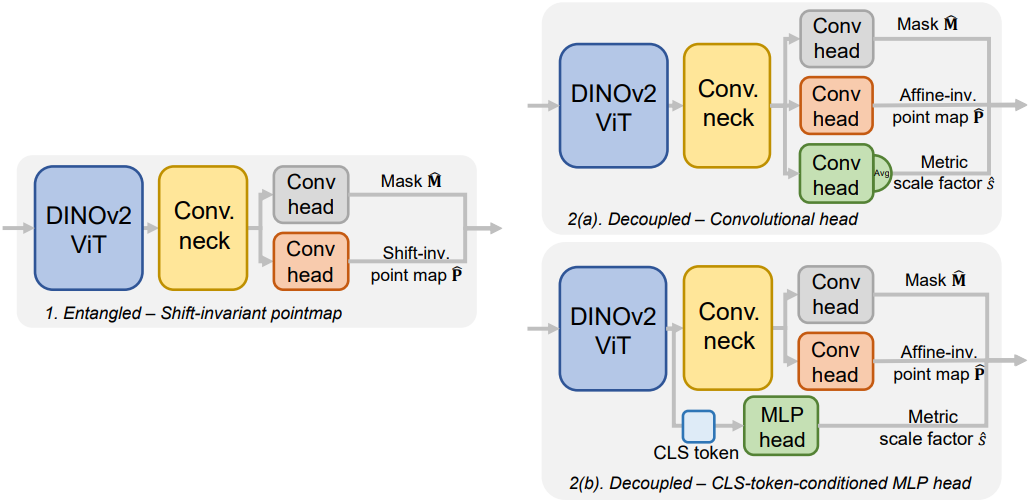
저자들은 MoGe를 metric scale 예측으로 확장하기 위한 두 가지 대안을 탐구했다.

Shift-invariant geometry prediction

MoGe의 자연스러운 확장은 affine-invariant point map에 metric scale $s$를 흡수하여 shift-invariant point map을 예측하는 동시에, 학습 과정에서 ROE alignment를 통해 global shift $\textbf{t}$를 계산하고 inference 시에 다시 해결하는 것이다. 이 디자인은 초점 거리 모호성을 우회하고 합리적인 metric 재구성 결과를 제공한다.

그러나 장면 스케일의 큰 변화로 인해 (ex. 실내 vs. 풍경), shift-invariant space에서 예측된 값은 넓은 범위를 포괄한다. 이는 scale 학습의 안정성을 떨어뜨리고, 부정확한 scale 예측은 relative geometry 학습을 방해하는 큰 gradient를 생성할 수 있다. 이러한 이유로 저자들은 scale 추정과 point map 예측을 완전히 분리하기로 결정했다.

Scale and relative geometry decomposition

Scale이 relative geometry 정확도에 영향을 미치는 것을 방지하기 위해 MoGe에서처럼 affine-invariant point map에 대한 geometry branch를 유지하고, 다음과 같은 scale 예측에 위한 추가 branch를 도입한다.

\[\begin{equation} \mathcal{L}_s = \| \log (\hat{s}) - \textrm{stopgrad} (\log (s^\ast)) \|_2^2 \end{equation}\]

$\hat{s}$는 예측된 metric scale이며, $s^\ast$는 예측된 affine-invariant point map $\hat{\textbf{P}}$에서 GT 사이에서 ROE solver를 사용하여 온라인으로 계산된 최적 scale이다. 최종 metric geometry는 예측된 scale과 affine-invariant point map을 곱하여 얻는다. 추가 scale 예측 branch에 대한 두 가지 디자인 옵션이 있다.

Convolutional head. 단순한 디자인은 convolutional head를 추가하여 단일 scale 값을 출력하고, convolution neck을 affine-invariant point map과 공유하는 것이다. 그러나 이 방식은 relative geometry 개선에 도움이 되지 않고 metric scale 예측을 저하시킨다. 단순히 convolutional head를 추가하면 대부분의 정보가 convolution neck에서 처리되어 scale 예측과 relative geometry에 미치는 영향을 분리하지 못한다. 또한, 작은 출력 head는 convolution neck에서 로컬 feature를 통합하는 데 효과적이지 않은 반면, 정확한 metric scale 예측에는 글로벌 정보가 필요하다.

CLS-token-conditioned MLP. Relative geometry와 metric scale 예측을 더욱 효과적으로 분리하기 위해, 두 번째 디자인은 MLP head를 사용하여 DINOv2 인코더의 CLS 토큰에서 metric scale을 직접 학습한다. 토큰의 글로벌 정보를 통해 네트워크는 정확한 metric scale을 예측할 수 있다. 이러한 간단한 디자인은 정확한 relative geometry를 유지하면서 convolutional head 방식보다 metric geometry 정확도를 향상시킨다. 따라서 저자들은 이 디자인을 최종적으로 채택하였다.

2. Real Data Refinement for Detail Recovery


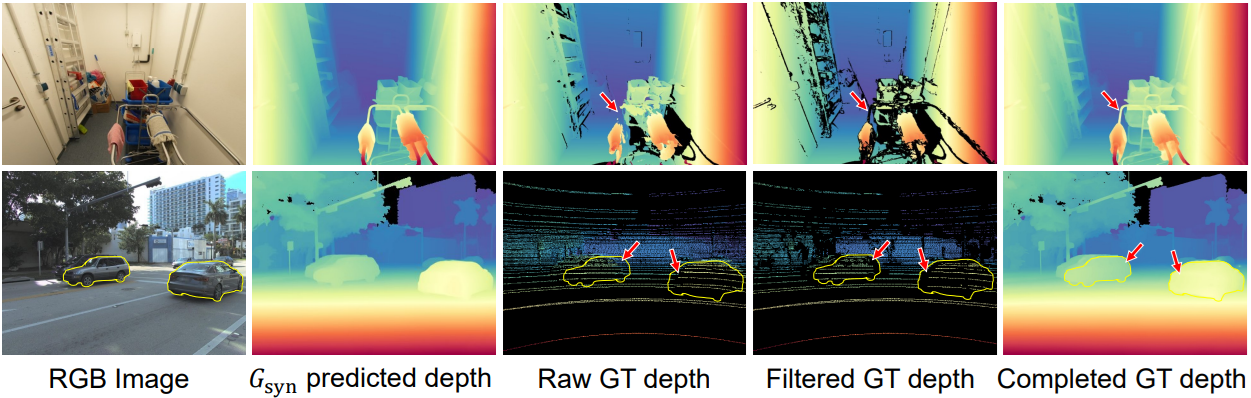
저자들은 MoGe 모델이 실제 학습 데이터의 노이즈와 불완전성으로 인해 세밀한 구조를 정확하게 재구성하는 데 어려움을 겪는다는 것을 발견했다. 그러나 합성 데이터는 현실의 다양성을 거의 포착하지 못하기 때문에 여전히 geometry 정확도에 한계가 있다. 따라서 실제 데이터를 사용하면서 노이즈와 불완전성을 줄이는 것은 정확한 geometry 추정을 위해 매우 중요하다. 이 문제를 해결하기 위해, 저자들은 실제 데이터에서 흔히 발생하는 실패 패턴을 완화하기 위해 합성 레이블을 통합하는 실제 데이터 정제 파이프라인을 설계했다.

실패 패턴 분석

실제 데이터는 종종 LiDAR 스캔이나 SfM 재구성에서 생성된다. LiDAR 데이터는 동기화 문제로 인해 깊이 및 색상 불일치가 발생할 수 있으며, 특히 물체 경계에서 그렇다. SfM 데이터는 반사 표면, 얇은 구조, 날카로운 경계와 같은 구조를 놓칠 수 있다. 본 논문의 정제 방식은 합성 데이터로 학습된 모델이 정확한 색상-깊이 매칭을 달성하고 선명하고 완전한 로컬 geometry를 포착한다는 사실을 활용한다. 이러한 pseudo label은 정확한 로컬 geometry가 주어졌을 때 잘못된 깊이를 걸러내고 실제 데이터에서 누락된 부분을 채우는 데 도움이 될 수 있다.

불일치 필터링


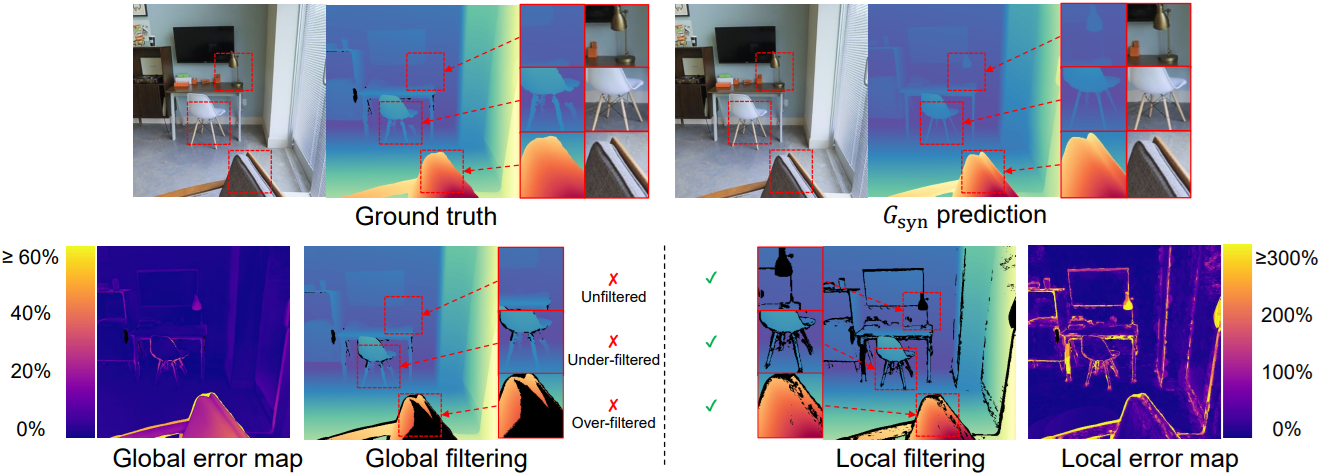
실제 촬영된 깊이 데이터를 필터링하기 위해, 합성 데이터만을 사용하여 MoGe 모델 \(G_\textrm{syn}\)를 학습시킨다. 그런 다음, \(G_\textrm{syn}\)로 실제 이미지에서 geometry를 추론한다. \(G_\textrm{syn}\)의 절대적인 깊이 예측에는 잠재적인 부정확성이 있으므로, 실제 깊이와 예측 깊이에서 로컬 영역의 상대적인 구조를 비교하는 데 중점을 둔다. 위치 \(\hat{\textbf{p}}_j\)의 각 추정 포인트에 대해, \(\hat{\textbf{p}}_j\)를 중심으로 하고 특정 반경 \(\hat{r}_j\)를 갖는 구형 영역 \(\hat{\mathcal{S}}_j\)를 샘플링한다.

\[\begin{equation} \hat{\mathcal{S}}_j = \{i \; \vert \; \| \hat{\textbf{p}}_i - \hat{\textbf{p}}_j \| \le \hat{r}_j, i \in \mathcal{M}\} \end{equation}\]

ROE solver를 통해 실제 캡처된 점 \(\{\textbf{p}_i\}_{i \in \hat{\mathcal{S}}_j}\)를 예측 \(\{\hat{\textbf{p}}_i\}_{i \in \hat{\mathcal{S}}_j}\)와 정렬하고 지정된 반경을 넘어 예측에서 벗어나는 경우 실제 캡처된 점을 outlier로 표시하여 집합 \(\mathcal{O}_j\)를 형성한다.

\[\begin{equation} \mathcal{O}_j = \{i \; \vert \; \| s_j^\ast \textbf{p}_i + \textbf{t}_j^\ast - \hat{\textbf{p}}_i \| > \hat{r}_j, i \in \} \end{equation}\]

\((s_j^\ast, \textbf{t}_j^\ast)\)를 로컬 영역에 대한 최적 alignment factor로 사용한다. 서로 다른 \(\hat{r}_j\)의 모든 샘플링된 로컬 영역에서 파생된 outlier 집합을 결합하고 마스크에서 제외하여 최종 유효 영역을 생성한다.

\[\begin{equation} \mathcal{M}_\textrm{filtered} = \mathcal{M} \setminus \left( \bigcup_j \mathcal{O}_j \right) \end{equation}\]

예측된 깊이와 실제 데이터를 로컬에서 비교하면 예측된 깊이의 절대적인 편향을 크게 피할 수 있다. 대신 global alignment를 사용하면 잘못된 필터링이 발생할 수 있다.

Geometry completion

불일치 영역을 필터링한 후, \(G_\textrm{syn}\)으로 예측된 ​​세부 구조와 남은 실제 깊이를 통합하여 완전한 depth map을 생성한다. 구체적으로, 필터링된 영역의 깊이 \(\{d_i^c\}_{i \in \mathcal{M}_\textrm{filtered}^c}\)를 log-space Poisson completion을 사용하여 재구성한다.

\[\begin{equation} \min \sum_{i \in \mathcal{M}_\textrm{filtered}^c} \| \nabla (\log d_i^c) - \nabla (\log \hat{d}_i) \|^2, \quad \textrm{s.t.} \quad d_i^c = d_i, \forall i \in \partial \mathcal{M}_\textrm{filtered}^c \end{equation}\]

(\(\mathcal{M}_\textrm{filtered}^c\)는 \(\mathcal{M}_\textrm{filtered}\)가 아닌 영역, \(\hat{d}_i\)와 $d_i$는 각각 \(G_\textrm{syn}\)로 예측한 깊이와 실제 획득한 깊이)

이 전략은 재구성된 깊이가 경계 조건으로 실제 깊이를 유지하면서 로컬 영역에서 예측된 깊이의 gradient와 일치하도록 한다.

본 방법은 LiDAR 스캔에서 불일치하는 깊이를 효과적으로 제거하고 SfM으로 재구성된 depth map에서 누락된 부분을 채운다. 완성된 depth map은 입력 이미지와 일치하는 선명한 기하학적 경계를 유지하는 동시에 원본 depth map의 robust한 절대적인 깊이를 유지한다. 정제된 학습 데이터는 모델의 선명도를 효과적으로 향상시키고 정확한 geometry 추정을 유지한다.

Experiments

  • 구현 디테일
    • backbone: DINOv2-ViT-Large
    • convolutional head: MoGe와 동일하지만 속도를 느리게 만드는 normalization layer를 제거
    • iteration: 12만
    • learning rate: backbone은 $1 \times 10^{-5}$, neck과 head는 $1 \times 10^{-4}$, 2.5만 iteration마다 절반
    • GPU: NVIDIA A100 32개로 120시간 학습

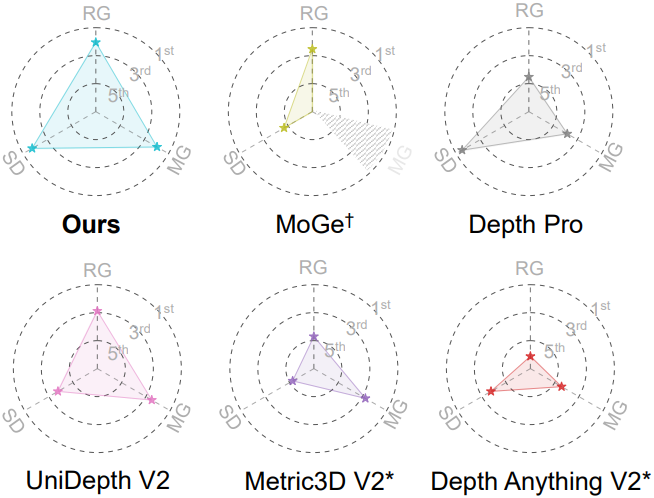
1. Quantitative Evaluation

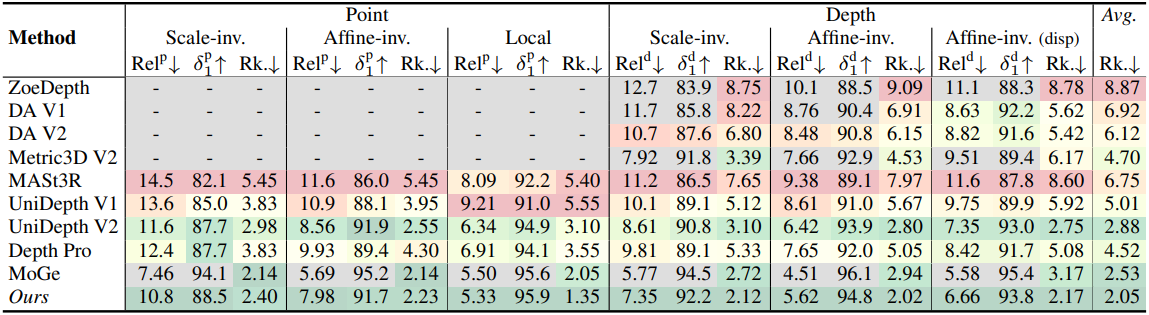
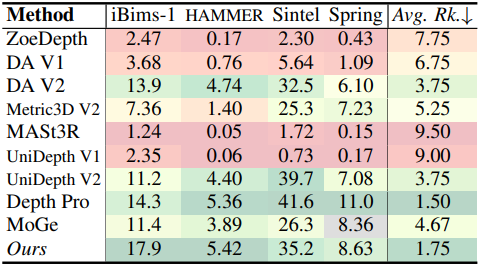
다음은 relative geometry에 대한 평가 결과이다.


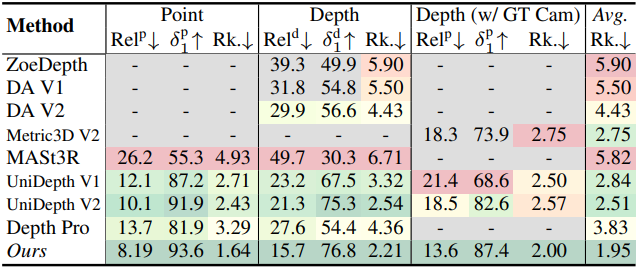
다음은 metric geometry에 대한 평가 결과이다.


다음은 boundary sharpness에 대한 평가 결과이다.

2. Qualitative Evaluation

다음은 metric scale의 point map과 disparity map을 비교한 결과이다.

3. Ablation Study

다음은 ablation study 결과이다.

You may also enjoy