[논문리뷰] MoGe: Unlocking Accurate Monocular Geometry Estimation for Open-Domain Images with Optimal Training Supervision

CVPR 2025 (Oral). [Paper] [Page] [Github]
Ruicheng Wang, Sicheng Xu, Cassie Dai, Jianfeng Xiang, Yu Deng, Xin Tong, Jiaolong Yang
USTC | Microsoft Research | Harvard | Tsinghua University
24 Oct 2024

Introduction

본 논문에서는 단일 이미지에서 3D geometry를 바로 추정하는 새로운 방법을 소개한다. 모델 아키텍처는 간단하고 직관적이다. 이미지에서 point map을 직접 예측하여 필요한 경우 depth map과 FOV를 도출할 수 있다. Scale-invariant point map을 사용하는 DUSt3R와 달리, 본 논문에서는 affine-invariant point map을 예측한다. 여기서 3D 포인트는 알려지지 않은 글로벌 scale과 3D shift의 영향을 받는다. 이러한 변화는 네트워크 학습에 해로운 초점 거리 모호성을 제거하기 때문에 중요하다.

하나의 이미지로부터 robust하고 정확한 point map 예측을 위해서는 학습 supervision 디자인이 필수적이다. 기존의 monocular depth estimation (MDE) 접근법과 마찬가지로, 학습 중 예측값을 실제 값과 일치시키기 위해 글로벌 scaling factor와 translation이 필요하다. 그러나 이러한 global alignment 계산을 위한 기존 방법들은 outlier에 민감하거나, 대략적인 근사치를 사용하여 계산되어 최적이 아닌 supervision을 초래한다. 본 논문에서는 affine-invariant point map loss에 대한 scale과 shift를 해결하기 위해 robust하고, 최적이며, 효율적인 (ROE) global alignment solver를 제안하며, 이는 학습 효과와 최종 정확도를 크게 향상시킨다.

또한, 로컬하고 영역별 geometry의 효과적인 학습은 이전에는 크게 간과되어 왔다. Monocular geometry 추정에서 서로 다른 물체 간의 상대적인 거리는 모호할 수 있으며, 이는 global alignment만 적용할 경우 정확한 로컬 geometry 학습을 방해한다. 이러한 점을 고려하여, 본 논문에서는 독립적인 affine 정렬 하에서 3D 포인트 클라우드의 로컬 불일치를 완화하는 multi-scale local geometry loss를 제안하였다. 이 디자인은 로컬 geometry 예측의 정확도를 크게 높였다.

Method

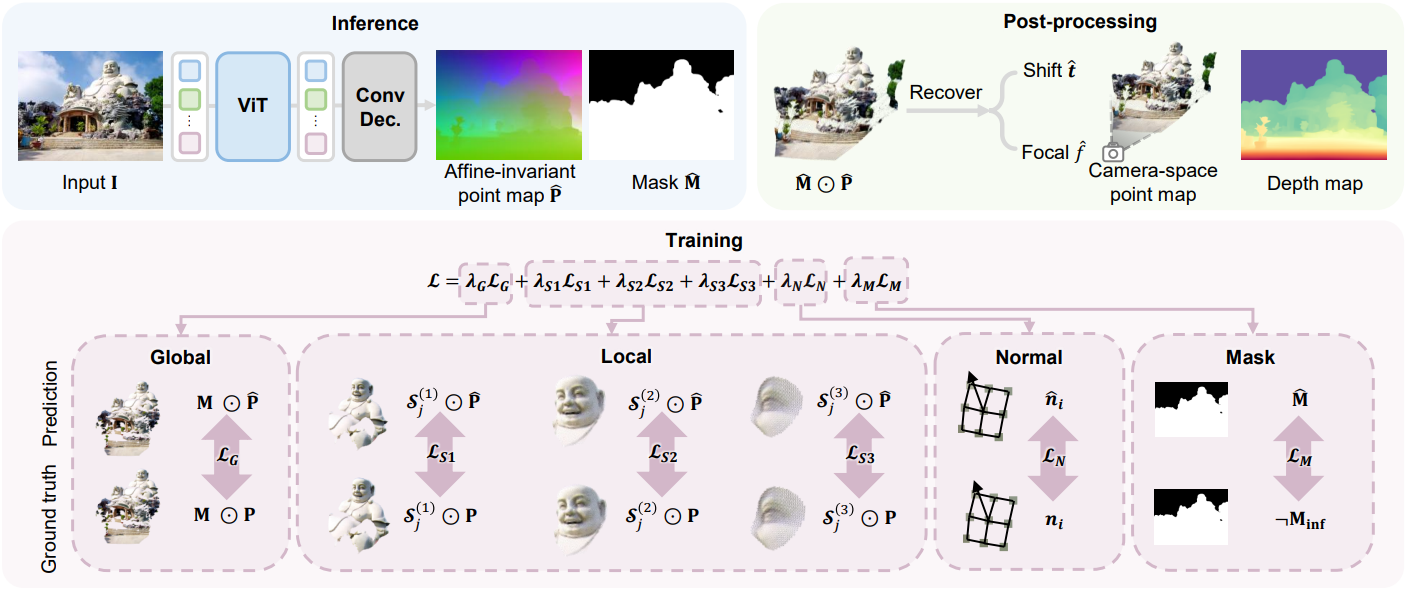
1. Affine-invariant point map

이미지 $\textbf{I} \in \mathbb{R}^{H \times W \times 3}$에 대해, 모델 $F_\theta$는 point map $\textbf{P} \in \mathbb{R}^{H \times W \times 3}$으로 표현되는 이미지 픽셀의 3D 좌표를 추론한다.

\[\begin{equation} F_\theta : \textbf{I} \rightarrow \textbf{P} \end{equation}\]

$\textbf{P}$의 좌표 프레임의 $X$축과 $Y$축은 각각 이미지 공간의 $u$축과 $v$축에 맞춰진다.

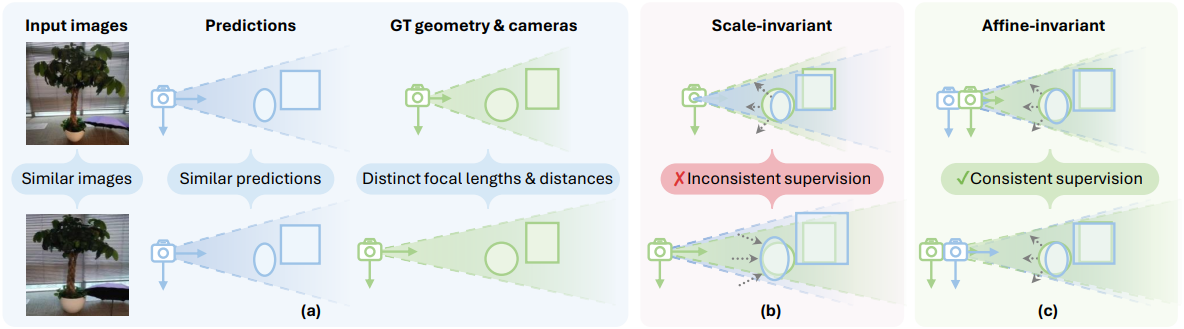
Monocular geometry 추정은 초점 거리 모호성으로 인해 종종 어려움을 겪는다. 이 문제를 해결하기 위해, 본 논문에서는 affine-invariant point map $\textbf{P}$를 예측하는 방법을 제안하였다. 즉, $\textbf{P}$는 글로벌 scale $s \in \mathbb{R}$와 offset $\textbf{t} \in \mathbb{R}^3$에 무관하므로, 임의의 $s$와 $\textbf{t}$에 대해 $\textbf{P} \simeq s \textbf{P} + \textbf{t}$이다. Scale-invariant 방식과 비교했을 때, 예측값과 실제값 간의 초점거리 및 카메라 위치 차이는 translation을 통해 보정된다. 이를 통해 초점 거리가 모호할 때 일관된 geometry supervision이 보장되어 더욱 효과적인 geometry 학습이 가능하다.

일반적으로 통용되는 관례에 따라, 카메라의 principal point가 이미지 중심에 있고 이미지가 정사각형이라고 가정한다. 이 경우, $\textbf{t}$는 $Z$축 shift $t_z$로 단순화할 수 있다 (즉, $t_x = t_y = 0$).

Recovering camera focal and shift

Affine-invariant point map 표현은 카메라 shift와 초점 거리를 모두 복원하는 데 사용할 수 있다. 예측된 3D 포인트 $(x_i, y_i, z_i)$와 그에 해당하는 2D 픽셀 $(u_i, v_i)$가 주어지면, projection error를 최소화하여 초점 거리 예측 $f$와 $Z$축 shift $t_z^\prime = t_z / s$를 구한다.

\[\begin{equation} \min_{f, t_z^\prime} \sum_{i=1}^N \left( \frac{f x_i}{z_i + t_z^\prime} - u_i \right)^2 + \left( \frac{f y_i}{z_i + t_z^\prime} - v_i \right)^2 \end{equation}\]

위 식은 빠른 반복 최적화 알고리즘을 사용하여 효율적으로 풀 수 있으며, 일반적으로 10 iteration 이내에 수렴하며, 약 3ms가 소요된다. $t_z^\prime$이 복구되면, 카메라 공간에서의 scale-invariant depth map과 point map은 $z$ 좌표에 $t_z^\prime$을 더하여 얻을 수 있다.

2. Training Objectives

Global point map supervision

$i$번째 픽셀에 대하여, \(\hat{\textbf{p}}_i\)를 예측된 3D 포인트라고 하고, \(\textbf{p}_i\)를 해당 GT라고 하자. Global point map loss는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L}_G = \sum_{i \in \mathcal{M}} \frac{1}{z_i} \| s \hat{\textbf{p}}_i + \textbf{t} - \textbf{p}_i \|_1 \end{equation}\]

($s$와 $\textbf{t}$는 예측된 affine-invariant point map을 GT 카메라 공간으로 변환하는 정렬 파라미터, $\mathcal{M}$은 레이블이 있는 영역의 마스크, $z_i$는 \(\textbf{p}_i\)의 $z$ 좌표)

가중치 항 $1/z_i$는 극단적인 깊이 변화에 걸쳐 학습 신호의 균형을 맞추기 위해 적용된다.

학습에 \(\mathcal{L}_G\)를 적용하려면 먼저 $s$와 $\textbf{t}$를 결정해야 한다. 기존의 affine-invariant 깊이 추정 방법은 두 집합의 중간 깊이를 앵커로 사용하여 shift를 계산한 후 scaling하거나 깊이 범위를 정규화하는 등 대략적인 정렬 근사법을 사용하는 경우가 많았다. 이러한 간단한 전략은 최적이 아닌 정렬을 초래하고 만족스럽지 못한 supervision으로 이어질 수 있다.

본 논문에서는 최적 정렬 파라미터를 도출하는 ROE solver를 제안하였다. 구체적으로, $s^\ast$와 \(\textbf{t}^\ast\)를 다음과 같이 결정한다.

\[\begin{equation} (s^\ast, \textbf{t}^\ast) = \underset{s, \textbf{t}}{\arg \min} \sum_{i \in \mathcal{M}} \frac{1}{z_i} \| s \hat{\textbf{p}}_i + \textbf{t} - \textbf{p}_i \|_1 \\ \textrm{where} \quad t_x = t_y = 0 \end{equation}\]

이 방정식을 푸는 한 가지 방식은 이를 absolute residuals 최적화 문제로 구성하고 linear programming 방법을 사용하는 것이다. 그러나 이러한 방법은 계산 복잡도가 높아 종종 $O(N^3)$을 초과하는 것으로 알려져 있어 계산에 몇 초가 걸릴 수 있는 수천 개의 포인트가 있는 네트워크 학습에는 비효율적이다.

대신 저자들은 효율적인 병렬 검색 알고리즘을 개발하였다. 최적값은 일부 인덱스 $k$에 대해 \(s \hat{z}_k + t_z\)일 때 발생해야 한다는 사실을 고려하여 $t_z$를 s로 대체하고 문제를 일련의 병렬 1차원 하위 ​​문제로 나눈다. 이렇게 하면 복잡도가 $O(N^2 \log N)$으로 줄어들고 효율적인 GPU 기반 학습이 가능해진다.

실제로, $L_1$ error norm을 적용하더라도 위 식은 outlier에 종종 민감하게 반응한다. 모델이 가까운 전경 픽셀을 먼 배경 점으로 잘못 예측하는 경우, loss는 이러한 잘못된 예측에 지배될 것이다. Robustness를 더욱 향상시키기 위해 absolute residual에 $\min(\cdot, \tau)$를 적용한다. 이러한 truncation은 non-convexity를 발하지만, 약간의 조정만으로도 solver를 적용할 수 있다.

Multi-scale local geometry loss

Monocular geometry 추정에서 서로 다른 물체 간의 상대적 거리는 모호하고 예측하기 어려울 수 있다. 이는 모든 물체에 대해 계산된 global alignment를 적용할 때 정확한 로컬 geometry 학습을 방해한다. 저자들은 로컬 geometry 학습에 대한 supervision을 강화하기 위해, 독립적인 정렬을 갖는 로컬 구면 영역의 정확도를 측정하는 loss function을 제안하였다.

구체적으로, GT 3D 포인트 \(\textbf{p}_j\)가 앵커로 주어지면, 먼저 다음과 같이 정의된 구 영역 내의 포인트 집합을 선택한다.

\[\begin{equation} \mathcal{S}_j = \{i \; \vert \; \| \textbf{p}_i - \textbf{p}_j \| \le r_j, i \in \mathcal{M} \} \\ \textrm{where} \quad r_j = \alpha \cdot z_j \cdot \frac{\sqrt{W^2 + H^2}}{2f} \end{equation}\]

($z_j$는 \(\textbf{p}_j\)의 $z$ 좌표, $f$는 GT 초점 거리, $W$와 $H$는 이미지의 너비와 높이)

이렇게 하면 hyperparameter $\alpha \in (0, 1)$은 projection된 구의 지름과 이미지 대각 길이의 비율을 근사화한다.

그런 다음, 앞서 언급한 ROE solver를 적용하여 point map을 최적의 \((s_j^\ast, \textbf{t}_j^\ast)\)로 정렬하고 오차를 계산한다. 각 구 크기 파라미터 $\alpha$에 대해 앵커 포인트 집합 \(\mathcal{H}_\alpha\)를 샘플링하고 loss를 다음과 같이 계산한다.

\[\begin{equation} \mathcal{L}_{S(\alpha)} = \sum_{j \in \mathcal{H}_\alpha} \ell_{\mathcal{S}_j} = \sum_{j \in \mathcal{H}_\alpha} \sum_{i \in \mathcal{S}_j} \frac{1}{z_i} \| s_j^\ast \hat{\textbf{p}}_i + \textbf{t}_j^\ast - \textbf{p}_i \|_1 \end{equation}\]

실제로는 1/4, 1/16, 1/64의 세 가지 $\alpha$를 사용하여 각각 loss function \(\mathcal{L}_{S_1}\), \(\mathcal{L}_{S_2}\), \(\mathcal{L}_{S_3}\)를 계산한다.

Normal loss

더 나은 표면 품질을 위해 예측된 point map에서 계산된 normal을 GT와 함께 추가로 학습시킨다.

\[\begin{equation} \mathcal{L}_N = \sum_{i \in \mathcal{M}} \angle (\hat{\textbf{n}}_i, \textbf{n}_i) \end{equation}\]

(\(\textbf{n}_i\)는 GT normal, \(\hat{\textbf{n}}_i\)는 이미지 그리드에서 인접한 모서리의 외적으로 계산)

Mask loss

실외 장면의 무한대 영역(ex. 하늘)과 물체만 있는 이미지의 밋밋한 배경은 정의되지 않은 geometry를 갖는다. 유효 포인트의 마스크 \(\hat{\textbf{M}} \in \mathbb{R}^{H \times W}\)를 예측하기 위해 1채널 출력 head를 사용한다.

\[\begin{equation} \mathcal{L}_M = \| \hat{\textbf{M}} - (1 - \textbf{M}_\textrm{inf}) \|_2^2 \end{equation}\]

합성 데이터의 경우, 실제 마스크는 쉽게 구할 수 있지만, 실제 실외 장면의 경우 SegFormer를 사용하여 하늘 마스크를 얻는다. Inference 시에 예측 마스크는 threshold 0.5로 binarize된다.

Experiments

• 구현 디테일
  • 인코더: DINOv2의 사전 학습된 ViT 인코더
  • 디코더: CNN 기반 업샘플러
  • learning rate: 인코더는 $5 \times 10^{-6}$, 디코더는 $5 \times 10^{-5}$, 10만 iteration마다 1/5
  • batch size: 256
  • 종횡비: 1:2과 2:1사이에서 샘플링
  • augmentation: color jittering, Gaussian blurring, JPEG compression-decompression, random cropping

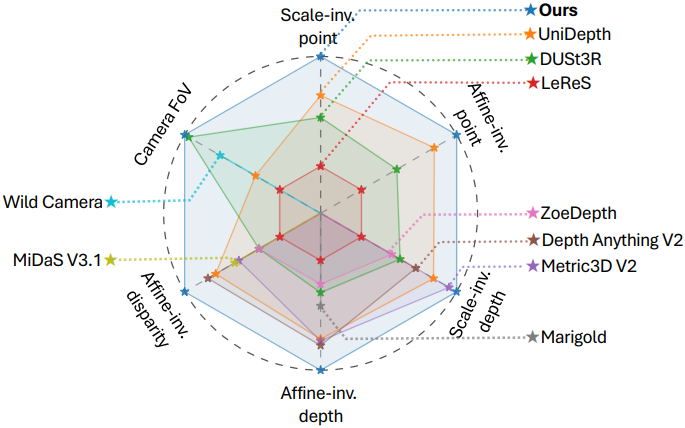
1. Quantitative Evaluations

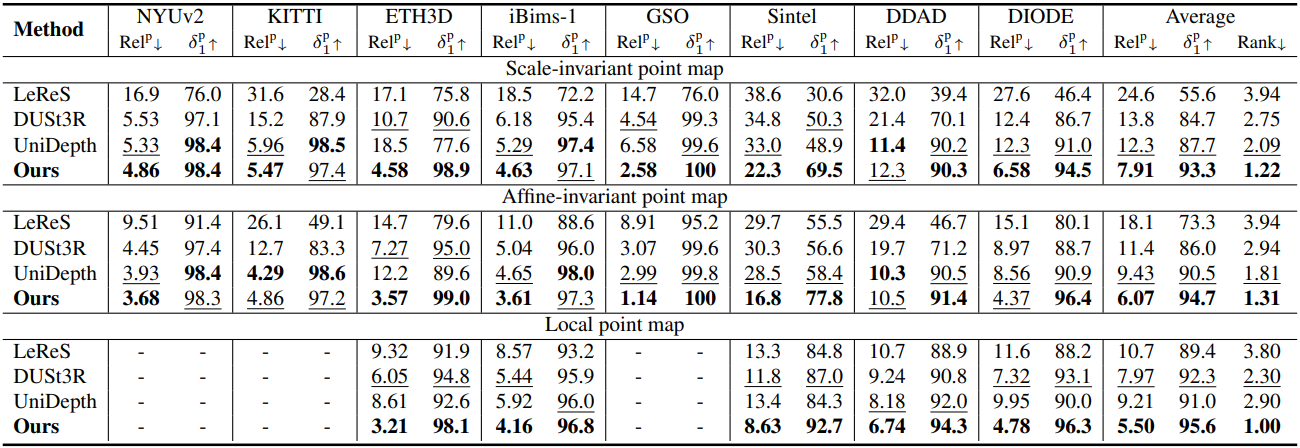
다음은 point map 추정 성능을 비교한 결과이다.

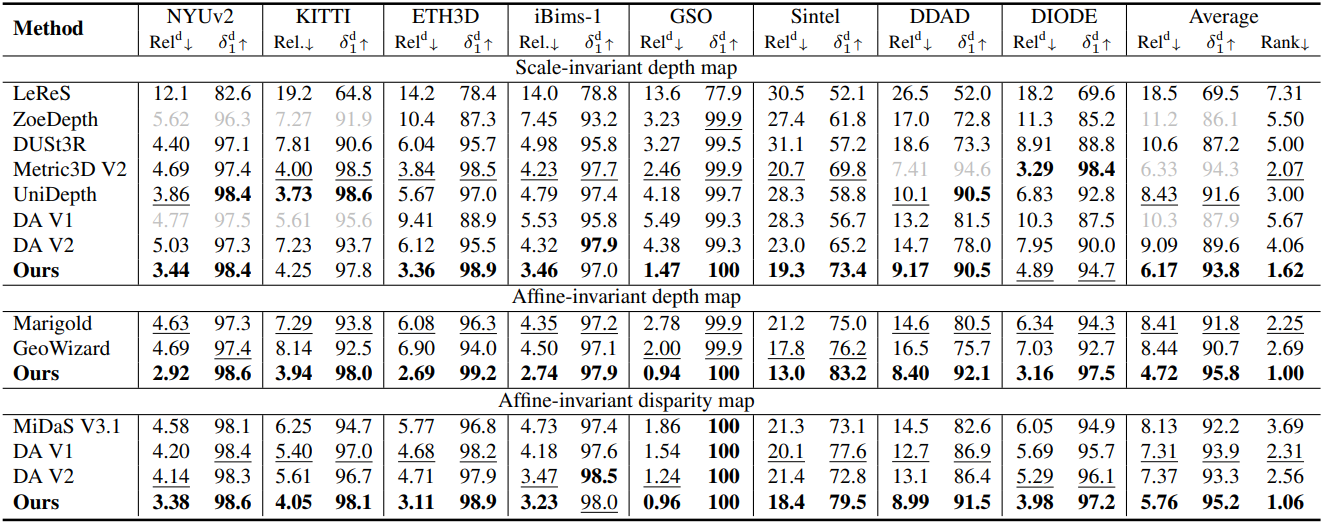
다음은 depth map 추정 성능을 비교한 결과이다.

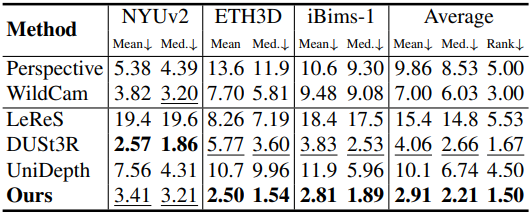
다음은 FOV 추정 성능을 비교한 결과이다.

2. Qualitative comparison

다음은 다른 모델들과 point map 및 disparity map을 비교한 결과이다.

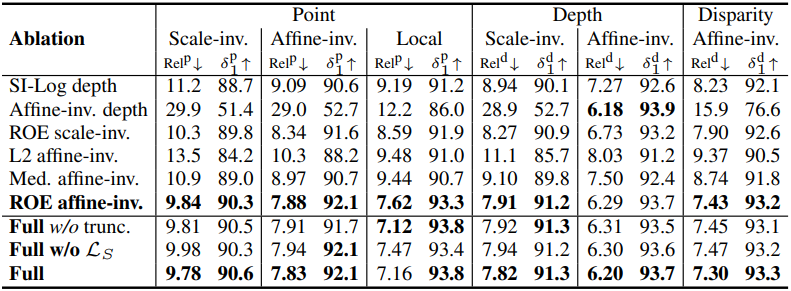
3. Ablation Study

다음은 ablation study 결과이다.