[논문리뷰] Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields

CVPR 2022 (Oral). [Paper] [Page] [Github]
Jonathan T. Barron, Ben Mildenhall, Dor Verbin, Pratul P. Srinivasan, Peter Hedman
Google | Harvard University
23 Nov 2021

Introduction

NeRF는 좌표 기반 MLP의 가중치 내에서 장면의 볼륨 밀도와 색상을 인코딩하여 장면의 매우 사실적인 렌더링을 합성한다. 이 접근 방식을 통해 사실적인 뷰 합성에 대한 상당한 진전이 가능해졌다. 그러나 NeRF는 광선을 따라 매우 작은 3D 포인트를 사용하여 MLP에 대한 입력을 모델링하므로 다양한 해상도의 뷰를 렌더링할 때 앨리어싱이 발생한다. mip-NeRF는 NeRF를 확장하여 원뿔을 따라 절두체를 추론함으로써 이 문제를 해결했다. 이로 인해 품질은 향상되지만 NeRF와 mip-NeRF는 카메라가 어떤 방향을 향하고 장면 콘텐츠가 어떤 거리에도 존재할 수 있는 무한한 장면을 처리할 때 어려움을 겪는다. 본 논문에서는 무한한 장면의 사실적인 렌더링을 생성할 수 있는 mip-NeRF 360이라고 하는 mip-NeRF의 확장판을 제시하였다.

제한이 없는 대규모 장면에 NeRF-like 모델을 적용하면 세 가지 중요한 문제가 발생한다.

1. Parameterization: 제한이 없는 360도 장면은 유클리드 공간의 임의의 넓은 영역을 차지할 수 있지만 mip-NeRF에서는 3D 장면 좌표가 제한된 도메인에 있어야 한다.
2. Efficiency: 크고 상세한 장면에는 더 많은 네트워크 용량이 필요하지만 학습 중에 각 광선을 따라 대규모 MLP를 조밀하게 쿼리하는 것은 비용이 많이 든다.
3. Ambiguity: 제한이 없는 장면의 콘텐츠는 거리에 상관없이 존재할 수 있으며 소수의 광선으로만 관찰되므로 2D 이미지에서 3D 콘텐츠를 재구성할 때 내재된 모호성이 더욱 악화된다.

Scene and Ray Parameterization

제한이 없는 장면에 대한 포인트의 parameterization에 대한 연구들이 있지만 이는 Gaussian을 reparameterize해야 하는 mip-NeRF에 대한 솔루션을 제공하지 않았다. 이를 위해 먼저 $f(x)$를 $\mathbb{R}^n \rightarrow \mathbb{R}^n$으로 매핑되는 부드러운 좌표 변환으로 정의하자. 이 함수의 선형 근사는 다음과 같다.

\[\begin{equation} f(\mathbf{x}) \approx f(\boldsymbol{\mu}) + \mathbf{J}_f (\boldsymbol{\mu}) (\mathbf{x} - \boldsymbol{\mu}) \end{equation}\]

여기서 \(\mathbf{J}_f (\boldsymbol{\mu})\)는 $\boldsymbol{\mu}$에서 $f$의 Jacobian이다. 이를 통해 다음과 같이 $f$를 $(\boldsymbol{\mu}, \mathbf{\Sigma})$에 적용할 수 있다.

\[\begin{equation} f(\boldsymbol{\mu}, \mathbf{\Sigma}) = (f(\boldsymbol{\mu}), \mathbf{J}_f (\boldsymbol{\mu}) \mathbf{\Sigma} \mathbf{J}_f (\boldsymbol{\mu})^\top) \end{equation}\]

이는 고전적인 칼만 필터와 동일하다. 여기서 $f$는 state transition model이다. $f$에 대한 선택은 다음과 같은 contraction이다.

\[\begin{equation} \textrm{contract} (\mathbf{x}) = \begin{cases} \mathbf{x} & \; \| \mathbf{x} \| \le 1 \\ \bigg( 2 - \frac{1}{\| \mathbf{x} \|} \bigg) \bigg( \frac{\mathbf{x}}{\| \mathbf{x} \|} \bigg) & \; \| \mathbf{x} \| > 1 \end{cases} \end{equation}\]

이 디자인은 NDC(normalized device coordinates)와 동일한 동기를 공유한다. 즉, 먼 지점은 거리가 아닌 시차(거리의 역수)에 비례하여 분포되어야 한다. 본 논문의 모델에서는 다음 식에 따라 유클리드 공간에서 mip-NeRF의 IPE feature를 사용하는 대신 이 축소된 공간에서 유사한 feature를 사용한다.

\[\begin{equation} \gamma (\textrm{contract} (\boldsymbol{\mu}, \mathbf{\Sigma})) \\ \textrm{where} \; \gamma (\boldsymbol{\mu}, \mathbf{\Sigma}) = \bigg\{ \begin{bmatrix} \sin (2^\ell \boldsymbol{\mu}) \exp (-2^{2 \ell - 1} \textrm{diag} (\mathbf{\Sigma})) \\ \cos (2^\ell \boldsymbol{\mu}) \exp (-2^{2 \ell - 1} \textrm{diag} (\mathbf{\Sigma})) \end{bmatrix} \bigg\}_{\ell = 0}^{L-1} \end{equation}\]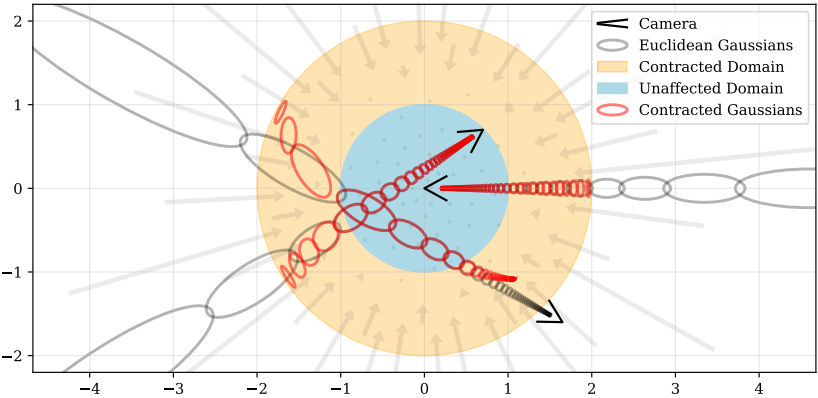

위 그림은 이 parameterization을 시각화한 것이다.

3D 좌표를 어떻게 parameterization해야 하는지에 대한 질문 외에도 광선 거리 $t$를 어떻게 선택해야 하는지에 대한 질문도 있다.

\[\begin{equation} t^c \sim \mathcal{U} [t_n, t_f], \quad \mathbf{t}^c = \textrm{sort} (\{t^c\}) \end{equation}\]

NeRF에서 이는 일반적으로 위 식에 따라 근거리 및 원거리 평면에서 균일하게 샘플링하여 수행된다. 그러나 NDC parameterization이 사용되는 경우 균일한 간격의 샘플들은 실제로 깊이의 역수(시차)에 균일한 간격으로 배치된다. 이 디자인 결정은 카메라가 한 방향만을 향할 때의 제한이 없는 장면에 적합하지만 모든 방향에서의 제한이 없는 장면에는 적용할 수 없다. 따라서 거리 $t$를 시차에 따라 선형적으로 명시적으로 샘플링한다.

시차 측면에서 광선을 parameterize하기 위해 유클리드 광선 거리 $t$와 정규화된 광선 거리 $s$ 사이의 가역 매핑을 정의한다.

\[\begin{equation} s = \frac{g(t) - g(t_n)}{g(t_f) - g(t_n)} \\ t = g^{-1} (s \cdot g(t_f) + (1-s) \cdot g(t_n)) \end{equation}\]

여기서 $g$는 가역 함수이다. 이는 $[t_n, t_f]$에 매핑되는 정규화된 광선 거리 $s \in [0, 1]$를 제공한다. $g(x) = 1/x$로 설정하면 공간에 균일하게 분포된 광선 샘플을 구성함으로써 $t$-거리가 시차적으로 선형으로 분포되는 광선 샘플을 생성한다. 본 논문의 모델에서는 $t$-거리를 사용하여 샘플링을 수행하는 대신 $s$-거리를 사용하여 샘플링을 수행한다. 이는 초기 샘플이 선형적으로 시차를 두고 배치될 뿐만 아니라 가중치 $w$의 개별 간격에서 후속 리샘플링도 유사하게 분포된다. 위 그림의 중앙에 있는 카메라에서 볼 수 있듯이, 광선 샘플의 선형 시차 간격은 균형을 이루는 $\textrm{contract}(\cdot)$을 나타낸다.

이러한 장면 좌표 공간의 설계를 통해 원래 NeRF 논문의 매우 효과적인 설정, 즉 제한된 공간 내에서의 균일한 간격의 광선 간격과 매우 유사한 제한이 없는 장면의 parameterization을 제공한다.

Coarse-to-Fine Online Distillation

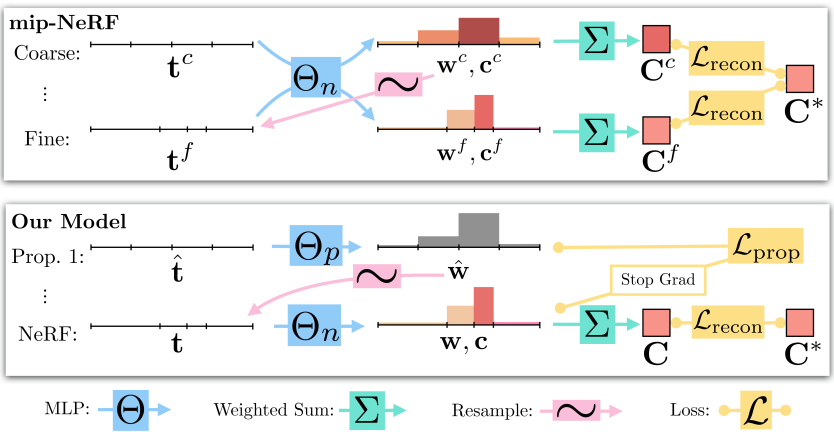
mip-NeRF는 MLP가 coarse ray interval을 사용하여 한 번 평가되고 다시 fine ray interval을 사용하여 평가되며, 두 수준 모두에서 이미지 재구성 loss를 사용하여 supervise되는 coarse-to-fine 리샘플링 전략을 사용한다. 대신에 mip-NeRF 360은 “NeRF MLP” $\Theta_\textrm{NeRF}$ (NeRF와 mip-NeRF에서 사용하는 MLP와 유사하게 동작함)와 “proposal MLP” $\Theta_\textrm{prop}$이라는 두 개의 MLP를 학습시킨다.

\[\begin{equation} w_i = \bigg( 1 - e^{- \tau_i (t_{i+1} - t_i)} \bigg) e^{- \Sigma_{i^\prime < i} \tau_{i^\prime} (t_{i^\prime + 1} - t_{i^\prime})} \end{equation}\]

proposal MLP는 위 식에 따라 proposal 가중치 벡터 \(\hat{\mathbf{w}}\)로 변환된 볼륨 밀도를 예측하지만 색상을 예측하지는 않는다. 이러한 proposal 가중치 \(\hat{\mathbf{w}}\)는 자체 가중치 벡터 $\mathbf{w}$를 예측하는 NeRF MLP에 제공되는 $s$-간격을 샘플링하는 데 사용된다. proposal MLP는 입력 이미지를 재현하도록 학습되지 않고 대신 NeRF MLP에 의해 생성된 가중치 $\mathbf{w}$를 제한하도록 학습된다. 두 MLP 모두 랜덤하게 초기화되고 공동으로 학습되므로 이 supervision은 NeRF MLP 지식을 proposal MLP에 대한 일종의 “online distillation”로 생각할 수 있다.

저자들은 큰 NeRF MLP와 작은 proposal MLP를 사용한다. 또한 많은 샘플을 사용하여 proposal MLP에서 반복적으로 평가하고 리샘플링하지만 NeRF MLP는 더 작은 샘플 집합으로 한 번만 평가한다. 이는 mip-NeRF보다 용량이 훨씬 높지만 학습 비용이 약간 더 비싼 것처럼 동작하는 모델을 제공한다. proposal 분포를 모델링하기 위해 작은 MLP를 사용하는 것은 정확도를 감소시키지 않는다. 이는 NeRF MLP를 distillation하는 것이 뷰 합성보다 더 쉬운 task임을 시사한다.

이 online distillation에는 proposal MLP \((\hat{\mathbf{t}}, \hat{\mathbf{w}})\)와 NeRF MLP $(\mathbf{t}, \mathbf{w})$의 히스토그램이 일관되도록 장려하는 loss function이 필요하다. 두 히스토그램 사이의 차이점을 최소화하는 것이 잘 정립된 task이기 때문에 처음에는 이 문제가 사소해 보일 수 있다. 그러나 히스토그램 $\mathbf{t}$와 $\hat{\mathbf{t}}$의 “bin”은 비슷할 필요가 없다. 실제로 proposal MLP가 성공적으로 집합을 선별하는 경우 장면 콘텐츠가 존재하는 거리의 $\mathbf{t}$와 $\hat{\mathbf{t}}$는 매우 다를 것이다.

여러 연구들에서 동일한 bin을 가진 두 히스토그램 간의 차이를 측정하기 위한 수많은 접근 방식이 제시되어 있지만 본 논문의 경우는 상대적으로 연구가 부족하다. 이 문제는 하나의 히스토그램 bin 내의 콘텐츠 분포에 대해 아무 것도 가정할 수 없기 때문에 어렵다. 가중치가 0이 아닌 구간은 해당 구간 전체에 걸쳐 균일한 가중치 분포, 해당 구간의 어느 위치에 있는 델타 함수 또는 수많은 다른 분포를 나타낼 수 있다. 따라서 저자들은 다음과 같은 가정 하에 loss를 구성하였다.

하나의 질량 분포를 사용하여 두 히스토그램을 설명할 수 있는 경우 loss는 0이어야 한다.

0이 아닌 loss는 두 히스토그램이 동일한 “실제” 질량 분포를 반영하는 것이 불가능한 경우에만 발생할 수 있다.

이를 위해 먼저 간격 $T$와 겹치는 모든 proposal 가중치의 합을 계산하는 함수를 정의한다.

\[\begin{equation} \textrm{bound} (\hat{\mathbf{t}}, \hat{\mathbf{w}}, T) = \sum_{j: T \cap \hat{T}_j \ne \varnothing} \hat{w}_j \end{equation}\]

만일 두 히스토그램이 서로 일치하면 $(\mathbf{t}, \mathbf{w})$의 모든 간격 $(T_i, w_i)$에 대해 \(w_i \le \textrm{bound} (\hat{\mathbf{t}}, \hat{\mathbf{w}}, T_i)\)를 유지해야 한다. Loss는 이 부등식을 위반하고 이 bound를 초과하는 잉여 히스토그램 질량에 불이익을 준다.

\[\begin{equation} \mathcal{L}_\textrm{prop} (\mathbf{t}, \mathbf{w}, \hat{\mathbf{t}}, \hat{\mathbf{w}}) = \sum_i = \frac{1}{w_i} \max (0, w_i - \textrm{bound} (\hat{\mathbf{t}}, \hat{\mathbf{w}}, T_i))^2 \end{equation}\]

이 loss는 NeRF MLP의 분포를 과소평가하기 위해 proposal 가중치에만 페널티를 적용하기를 원하기 때문에 비대칭이다. proposal 가중치가 NeRF 가중치보다 더 coarse하기 때문에 그 위에 upper envelope를 형성하므로 과대평가가 예상된다. $w_i$로 나누면 bound에 대한 이 loss의 기울기가 bound가 0일 때 일정한 값이 되도록 보장하여 올바르게 동작하는 최적화를 유도한다. $\mathbf{t}$와 $\hat{\mathbf{t}}$는 정렬되어 있으므로 summed-area table을 사용하여 위 식을 효율적으로 계산할 수 있다. 이 loss는 거리 $t$의 단조 변환에 불변하므로 ($\mathbf{w}$와 $\hat{\mathbf{w}}$가 이미 $t$-공간에서 계산되었다고 가정) 유클리드 광선 $t$-거리에 적용하든 정규화된 광선 $s$-거리에 적용하든 동일하게 동작한다.

NeRF 히스토그램 $(\mathbf{t}, \mathbf{w})$과 모든 proposal 히스토그램 \((\hat{\mathbf{t}}^k, \hat{\mathbf{w}})^k\) 사이에 이 loss를 부과한다. NeRF MLP는 mip-NeRF에서와 같이 입력 이미지에 대한 재구성 loss \(\mathcal{L}_\textrm{recon}\)을 사용하여 supervise된다. NeRF MLP가 리드하고 proposal MLP가 따르도록 \(\mathcal{L}_\textrm{prop}\)을 계산할 때 NeRF MLP의 출력 $\mathbf{t}$와 $\mathbf{w}$에 stop-gradient를 배치한다. 그렇지 않으면 NeRF가 proposal MLP의 task를 덜 어렵게 만들기 위해 장면을 더 나쁘게 재구성하도록 권장될 수 있다.

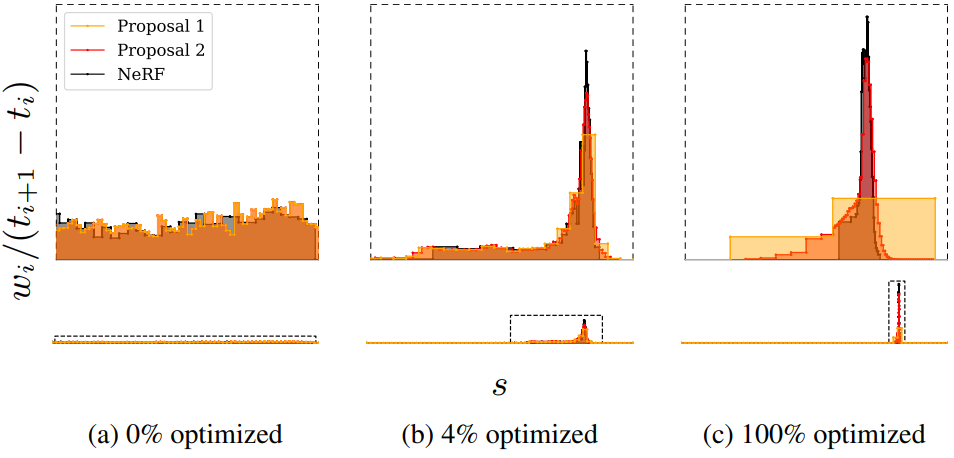
이 proposal supervision의 효과는 위 그림에서 볼 수 있다. 여기서 NeRF MLP는 장면의 표면 주위에 가중치 $\mathbf{w}$를 점차적으로 국한시키는 반면 proposal MLP는 NeRF 가중치를 포괄하는 대략적인 proposal 히스토그램을 따라잡아 예측한다.

Regularization for Interval-Based Models

학습된 NeRF는 종종 위 그림의 (a)에 표시된 “floaters”와 “background collapse”라고 부르는 두 가지 특징적인 아티팩트를 나타낸다.

1. Floater: 입력 뷰의 일부 측면을 설명하지만 다른 각도에서 보면 흐릿한 구름처럼 보이는 볼륨 밀도가 높은 공간의 작은 단절된 영역
2. Background collapse: 멀리 있는 표면이 카메라에 가까운 dense한 콘텐츠의 반투명 구름으로 잘못 모델링되는 현상

저자들은 볼륨 밀도에 noise를 주입하는 데 NeRF의 방법보다 floaters와 background collapse를 더 효과적으로 방지하는 regularizer를 제시하였다.

Regularizer는 각 광선을 parameterize하는 정규화된 광선 거리의 집합 $\mathbf{s}$와 가중치의 집합 $\mathbf{w}$로 정의된 step function으로 간단하게 정의된다.

\[\begin{equation} \mathcal{L}_\textrm{dist} (\mathbf{s}, \mathbf{w}) = \iint_{-\infty}^{\infty} \mathbf{w}_\mathbf{s} (u) \mathbf{w}_\mathbf{s} (v) \vert u - v \vert d_u d_v \end{equation}\]

여기서 \(\mathbf{w}_\mathbf{s} (u)\)는 $u$에서 $(\mathbf{s}, \mathbf{w})$에 의해 정의된 step function에 대한 보간이다.

\[\begin{equation} \mathbf{w}_\mathbf{s} (u) = \sum_i w_i \unicode{x1D7D9}_{[s_i, s_{i+1})]} (u) \end{equation}\]

$\mathbf{t}$를 사용하면 먼 간격의 가중치가 크게 증가하고 가까운 간격이 효과적으로 무시되기 때문에 정규화된 광선 거리 $\mathbf{s}$를 사용한다. 이 loss는 NeRF MLP에 의해 각 점에 할당된 가중치 $w$ 의해 조정된 이 1D step function을 따라 모든 점 쌍 사이의 거리를 적분한 것이다. 이것을 “distortion”이라고 부르는데, 이는 k-means에 의해 최소화된 distortion의 연속적인 버전과 유사하기 때문이다. 이 loss는 $\mathbf{w} = \mathbf{0}$으로 설정하여 최소화된다. 이것이 가능하지 않은 경우 (즉, 광선이 비어 있지 않은 경우) 가중치를 가능한 한 작은 영역으로 통합하여 최소화된다.

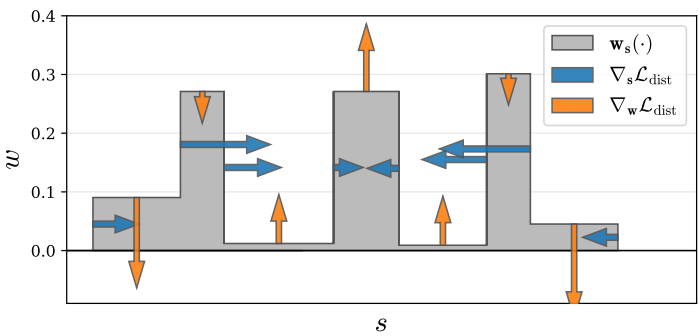
위 그림은 toy 히스토그램에서 이러한 loss의 기울기를 보여준다.

\(\mathcal{L}_\textrm{dist} (\mathbf{s}, \mathbf{w})\)는 정의하기가 간단하지만 계산하기가 쉽지 않다. 그러나 \(\mathbf{w}_\mathbf{s} (\cdot)\)는 각 간격 내에서 상수 값을 갖기 때문에 다음과 같이 다시 쓸 수 있다.

\[\begin{aligned} \mathcal{L}_\textrm{dist} (\mathbf{s}, \mathbf{w}) &= \sum_{i,j} w_i w_j \bigg\vert \frac{s_i + s_{i+1}}{2} - \frac{s_j + s_{j+1}}{2} \bigg\vert \\ &+ \frac{1}{3} \sum_i w_i^2 (s_{i+1} - s_i) \end{aligned}\]

이 식에서는 distortion loss를 계산하기가 간단하다. 이 재정의는 이 loss가 어떻게 동작하는지에 대한 어떤 직관도 제공한다. 첫 번째 항은 모든 간격의 중점 쌍 간의 가중 거리를 최소화하고, 두 번째 항은 각 개별 간격의 가중 크기를 최소화한다.

Optimization

저자들은 4개의 레이어와 256개의 hidden unit이 있는 proposal MLP와 8개의 레이어와 1024개의 hidden unit이 있는 NeRF MLP를 사용하였다. 둘 다 ReLU activation과 밀도 $\tau$에 대한 softplus activation을 사용한다. \((\hat{\mathbf{s}}^0, \hat{\mathbf{w}}^0)\)와 \((\hat{\mathbf{s}}^1, \hat{\mathbf{w}}^1)\)을 생성하기 위해 각각 64개의 샘플을 사용하여 proposal MLP를 평가하고 리샘플링한 다음, \((\mathbf{s}, \mathbf{w})\)를 생성하기 위해 32개의 샘플을 사용하여 NeRF MLP를 평가한다. 다음과 같은 loss를 최소화한다.

\[\begin{equation} \mathcal{L}_\textrm{recon} (\mathbf{C}(\mathbf{t}), \mathbf{C}^\ast) + \lambda \mathcal{L}_\textrm{dist} (\mathbf{s}, \mathbf{w}) + \sum_{k=0}^1 \mathcal{L}_\textrm{prop} (\mathbf{s}, \mathbf{w}, \hat{\mathbf{s}}^k, \hat{\mathbf{w}}^k) \end{equation}\]

각 batch의 모든 광선에 대한 평균을 계산한다. $\lambda$ hyperparameter는 데이터 항 \(\mathcal{L}_\textrm{recon}\)과 regularizer \(\mathcal{L}_\textrm{dist}\)의 균형을 유지한다. 모든 실험에서 $\lambda = 0.01$로 설정되었다. \(\mathcal{L}_\textrm{prop}\)에 사용된 stop-gradient는 $\Theta_\textrm{NeRF}$의 최적화와 독립적으로 $\Theta_\textrm{prop}$의 최적화를 수행하므로 \(\mathcal{L}_\textrm{prop}\)의 효과를 확장하기 위한 hyperparameter가 필요하지 않다. \(\mathcal{L}_\textrm{recon}\)의 경우 Charbonnier loss

\[\begin{equation} \sqrt{(x - x^\ast)^2 + \epsilon^2} \end{equation}\]

를 사용한다 ($\epsilon = 0.001$). 이는 mip-NeRF에서 사용되는 평균 제곱 오차보다 약간 더 안정적인 최적화를 달성한다.

저자들은 mip-NeRF 학습 일정의 약간 수정된 버전을 사용하여 모델을 학습시켰다.

• optimizer: Adam ($\beta_1 = 0.9$, $\beta_2 = 0.999$, $\epsilon = 10^{-6}$)
• batch size: $2^{14}$
• iteration: 25만
• learning rate: $2 \times 10^{-3}$에서 $2 \times 10^{-5}$까지 로그 선형적으로 어닐링
• warmup: 512 iteration
• gradient clipping: $10^{-3}$

Results

Comparative evaluation

다음은 여러 이전 방법들과 정량적으로 비교한 표이다.

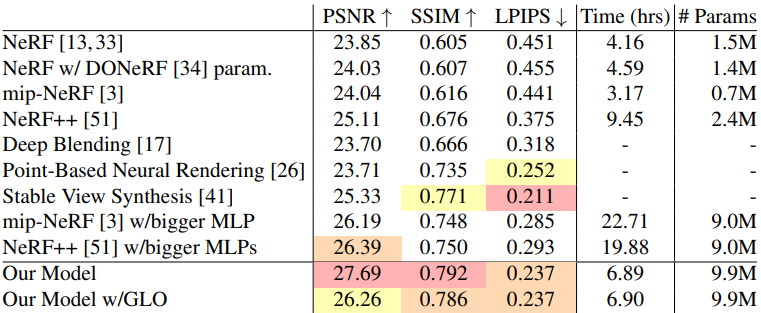
다음은 여러 이전 방법들과 결과를 비교한 것이다.

Ablation study

다음은 ablation study 결과이다.

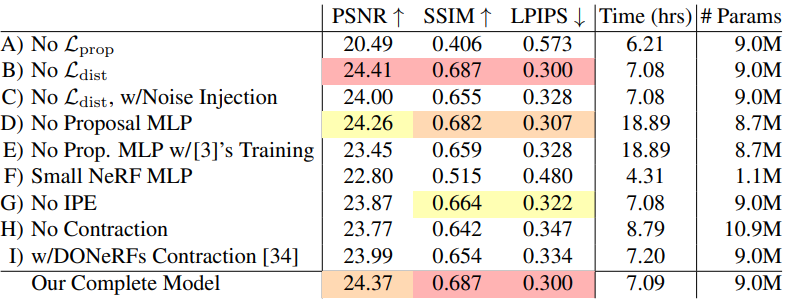
Limitations

1. 일부 얇은 구조와 미세한 디테일이 누락될 수 있다.
2. 카메라가 장면 중앙에서 멀리 이동하면 뷰 합성 품질이 저하될 수 있다.
3. 대부분의 NeRF-like 모델과 마찬가지로 장면을 복구하려면 몇 시간의 학습이 필요하다.