Diffusion은 신이고 GPT는 무적이다

ICCV 2021. [Paper] [Page] [Github]
Jonathan T. Barron, Ben Mildenhall, Matthew Tancik, Peter Hedman, Ricardo Martin-Brualla, Pratul P. Srinivasan
Google | UC Berkeley
24 Mar 2021

Introduction

NeRF와 같은 표현은 사실적인 새로운 뷰를 렌더링할 목적으로 이미지의 3D 객체와 장면을 표현하는 방법을 학습하기 위한 강력한 전략으로 등장했다. NeRF는 다양한 뷰 합성 task에서 인상적인 결과를 보여줬지만 NeRF의 렌더링 모델에는 과도한 흐릿함과 앨리어싱을 유발할 수 있는 결함이 있다. NeRF는 전통적인 이산적으로 샘플링된 형상을 입력 5D 좌표 (3D 위치 + 2D 뷰 방향)에서 장면 속성 (volume density와 뷰에 따라 방출되는 radiance)으로 매핑하는 연속 함수로 대체하며, 이 연속 함수는 MLP로 parameterize된다. 픽셀의 색상을 렌더링하기 위해 NeRF는 해당 픽셀에서 하나의 광선을 캐스팅하고 해당 광선을 따라 샘플에서 장면 속성에 대해 MLP를 쿼리하고 이러한 값을 단일 색상으로 합성한다.

이 접근 방식은 모든 학습 및 테스트 이미지가 거의 일정한 거리에서 장면 내용을 관찰할 때 잘 작동하지만, NeRF 렌더링은 덜 인위적인 시나리오에서 상당한 아티팩트를 나타낸다. 학습 이미지가 여러 해상도에서 장면 콘텐츠를 관찰할 때 복구된 NeRF의 렌더링은 가까운 뷰에서 지나치게 흐릿하게 나타나고 먼 뷰에서는 앨리어싱 아티팩트를 포함한다. 간단한 해결책은 오프라인 raytracing에 사용되는 전략을 채택하는 것이다. 즉, 하나의 픽셀에서 여러 광선에 대하여 ray marching을 하여 각 픽셀을 슈퍼샘플링하는 것이다. 그러나 이는 하나의 광선을 렌더링하는 데 수백 번의 MLP 평가가 필요하고 하나의 장면을 재구성하는 데 몇 시간이 필요한 NeRF와 같은 표현의 경우 엄청나게 비용이 많이 든다.

본 논문에서는 저자들은 컴퓨터 그래픽 렌더링 파이프라인에서 앨리어싱을 방지하는 데 사용되는 mipmapping 접근 방식에서 영감을 얻었다. Mipmap은 서로 다른 이산적인 다운샘플링 스케일 집합에서 신호(일반적으로 이미지 또는 텍스처 맵)를 나타내고, 해당 광선과 교차하는 형상에 대한 픽셀 공간의 projection을 기반으로 광선에 사용할 적절한 스케일을 선택한다. 안티앨리어싱의 계산 부담이 렌더링에서 사전 계산 단계로 이동하기 때문에 이 전략을 pre-filtering이라고 한다. Mipmap은 주어진 텍스처에 대해 해당 텍스처가 렌더링된 횟수에 관계없이 한 번만 생성하면 된다.


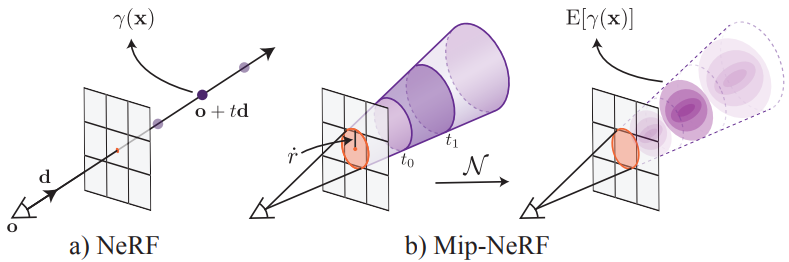
mip-NeRF라고 부르는 본 논문의 솔루션은 NeRF를 확장하여 연속적인 스케일 공간에 대해 pre-filtering된 radiance field를 동시에 나타낸다. Mip-NeRF에 대한 입력은 radiance field가 통합되어야 하는 영역을 나타내는 3D Gaussian이다. 위 그림에서 볼 수 있듯이, 픽셀에 해당하는 원뿔 절두체(conical frustum)를 근사화하는 Gaussian을 사용하며, 원뿔을 따라 간격마다 mip-NeRF를 쿼리하여 pre-filtering된 픽셀을 렌더링할 수 있다. 3D 위치와 주변 Gaussian 영역을 인코딩하기 위해 본 논문은 integrated positional encoding(IPE)이라는 새로운 feature 표현을 제안하였다. 이는 공간의 단일 포인트가 아닌 공간 영역을 컴팩트하게 featurize할 수 있는 NeRF의 positional encoding(PE)을 일반화한 것이다.

mip-NeRF는 NeRF의 정확도를 크게 향상시키며, 이러한 이점은 장면 콘텐츠가 다양한 해상도에서 관찰되는 상황에서 더욱 커진다 (ex. 카메라가 장면에서 더 가까워지고 멀어지는 설정). mip-NeRF는 까다로운 다중 해상도 벤치마크에서 NeRF에 비해 오차율을 평균 60%까지 줄일 수 있다. mip-NeRF의 스케일 인식 구조를 사용하면 계층적 샘플링을 위해 NeRF에서 사용하는 별도의 “coarse” MLP와 “fine” MLP를 하나의 MLP로 병합할 수 있다. 결과적으로 mip-NeRF는 NeRF보다 약간 빠르며(~7%) 파라미터 수가 절반이다.

Method

NeRF의 포인트 샘플링은 샘플링 및 앨리어싱과 관련된 문제에 취약하다. 픽셀의 색상은 절두체(frustum) 내에서 들어오는 모든 빛의 통합이지만 NeRF는 픽셀당 극도로 좁은 단일 광선을 투사하여 앨리어싱을 발생시킨다. mip-NeRF는 각 픽셀에서 원뿔을 캐스팅하여 이 문제를 개선하였다. 각 광선을 따라 포인트 샘플링을 수행하는 대신 캐스팅되는 원뿔을 일련의 원뿔 절두체(conical frustum)로 나눈다. 그리고 공간의 극히 작은 포인트에서 positional encoding (PE) feature들을 구성하는 대신 각 원뿔 절두체가 포함하는 볼륨의 integrated positional encoding (IPE) 표현을 구성한다. 이러한 변경을 통해 MLP는 중심이 아닌 각 원뿔 절두체의 크기와 모양을 추론할 수 있다.


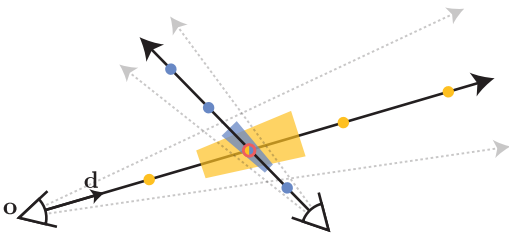
NeRF의 스케일에 대한 둔감함과 이 문제에 대한 mip-NeRF의 솔루션으로 인한 모호성은 위 그림에 시각화되어 있다. NeRF는 각 픽셀의 광선을 따라 포인트 샘플링된 PE feature(그림에서 점으로 표시)를 추출하는 방식으로 작동한다. 이러한 포인트 샘플링 feature는 각 광선이 보는 볼륨의 모양과 크기를 무시하므로 서로 다른 스케일에서 동일한 위치를 이미징하는 두 개의 서로 다른 카메라가 동일한 모호한 포인트 샘플링 feature를 생성하여 NeRF의 성능을 크게 저하시킬 수 있다. 이와 대조적으로 mip-NeRF는 광선 대신 원뿔을 캐스팅하고 샘플링된 각 원뿔 절두체(그림에서 사다리꼴로 표시)의 볼륨을 명시적으로 모델링하여 이러한 모호성을 해결한다.

원뿔 절두체와 IPE feature를 사용하면 NeRF의 “coarse” MLP와 “fine” MLP를 하나의 멀티스케일 MLP로 줄일 수 있으며, 이를 통해 학습 및 평가 속도를 높이고 모델 크기를 50% 줄였다.

1. Cone Tracing and Positional Encoding


NeRF에서와 마찬가지로 mip-NeRF의 이미지는 한 번에 한 픽셀씩 렌더링되므로 렌더링되는 개별 관심 픽셀의 관점에서 절차를 설명할 수 있다. 해당 픽셀에 대해 카메라의 projection의 중심 $\mathbf{o}$에서 픽셀 중심을 통과하는 방향 $\mathbf{d}$를 따라 원뿔을 캐스팅한다. 해당 원뿔의 꼭짓점은 $\mathbf{o}$에 있고 이미지 평면 $\mathbf{o} + \mathbf{d}$에서 원뿔의 반경은 $\dot{r}$로 parameterize된다. 저자들은 $\dot{r}$을 월드 좌표에서의 픽셀 너비의 $2 / \sqrt{12}$로 설정했다. 두 $t$ 값 $[t_0, t_1]$ 사이의 원뿔 절두체 내에 있는 위치의 집합 $\mathbf{x}$는 다음과 같다.

\[\begin{aligned} F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1) = \unicode{x1D7D9} \bigg\{ & \bigg( t_0 < \frac{\mathbf{d}^\top (\mathbf{x} - \mathbf{o})}{\| \mathbf{d} \|_2^2} < t_1 \bigg) \\ & \wedge \bigg( \frac{\mathbf{d}^\top (\mathbf{x}-\mathbf{o})}{\| \mathbf{d} \|_2 \| \mathbf{x}-\mathbf{o} \|_2} > \frac{1}{\sqrt{1 + (\dot{r} / \| \mathbf{d} \|_2)^2}}\bigg) \bigg\} \end{aligned}\]

여기서 \(\unicode{x1D7D9}\{\cdot\}\)은 indicator function으로, $\mathbf{x}$가 $(\mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1)$에 의해 정의된 원뿔 절두체 내에 있는 경우에만 $F(\mathbf{x}, \cdot) = 1$이다.

이제 이 원뿔 절두체 내부에 있는 볼륨의 featurize된 표현을 구성해야 한다. 이상적으로, 이 featurize된 표현은 NeRF에서 사용되는 PE feature와 유사한 형식이어야 하며, 이는 PE feature 표현이 NeRF의 성공에 매우 중요하기 때문이다. 이에 대한 접근 방식은 많이 있지만 저자들이 찾은 가장 간단하고 효과적인 해결책은 원뿔 절두체 내에 있는 모든 좌표의 PE의 기대값을 간단히 계산하는 것이다.

\[\begin{equation} \gamma^\ast (\mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1) = \frac{\int \gamma(\mathbf{x}) F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1) d\mathbf{x}}{\int F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1) d\mathbf{x}} \end{equation}\]

그러나 분자의 적분에는 closed form solution이 없기 때문에 이 feature를 어떻게 효율적으로 계산할 수 있는지는 불분명하다. 따라서 저자들은 원하는 feature에 대한 효율적인 근사를 허용하는 multivariate Gaussian을 사용하여 원뿔 절두체를 근사하였다. 이를 integrated positional encoding (IPE)이라고 부른다.

Multivariate Gaussian을 사용하여 원뿔 절두체를 근사화하려면 $F(\mathbf{x}, \cdot)$의 평균과 공분산을 계산해야 한다. 각 원뿔 절두체는 원형으로 가정되고 원뿔 절두체는 원뿔 축을 중심으로 대칭이기 때문에 Gaussian은 세 가지 값으로 완전히 특성화된다.

  1. $\mu_t$: 광선에 대한 평균 거리
  2. $\sigma_t^2$: 광선에 대한 분산
  3. $\sigma_r^2$: 광선에 수직인 분산

각 값은 다음과 같이 계산된다.

\[\begin{aligned} \mu_t &= t_\mu + \frac{2 t_\mu t_\delta^2}{3 t_\mu^2 + t_\delta^2} \\ \sigma_t^2 &= \frac{t_\delta^2}{3} - \frac{4 t_\delta^4 (12 t_\mu^2 - t_\delta^2)}{15 (3 t_\mu^2 + t_\delta^2)} \\ \sigma_r^2 &= \dot{r}^2 \bigg( \frac{t_\mu^2}{4} + \frac{5 t_\delta^2}{12} - \frac{4 t_\delta^4}{15 (3 t_\mu^2 + t_\delta^2)} \bigg) \end{aligned}\]

이러한 값들은 중간점 $t_\mu = (t_0 + t_1)/2$와 반폭 $t_\delta = (t_1 − t_0)/2$에 대해 parameterize되며 이는 수치 안정성에 매우 중요하다. 이 Gaussian을 원뿔 절두체의 좌표계에서 다음과 같이 월드 좌표계로 변환할 수 있으며, 이를 통해 최종 multivariate Gaussian을 얻을 수 있다.

\[\begin{aligned} \boldsymbol{\mu} &= \mathbf{o} + \mu_t \mathbf{d} \\ \mathbf{\Sigma} &= \sigma_t^2 (\mathbf{d} \mathbf{d}^\top) + \sigma_r^2 \bigg(\mathbf{I} - \frac{\mathbf{d} \mathbf{d}^\top}{\| \mathbf{d} \|_2^2} \bigg) \end{aligned}\]

다음으로, 앞서 언급한 Gaussian에 따라 분포된 위치적으로 인코딩된 좌표에 대한 기대값인 IPE를 도출한다. PE를 Fourier feature로 다시 쓰면 다음과 같다.

\[\begin{equation} \mathbf{P} = \begin{bmatrix} 1 & 0 & 0 & 2 & 0 & 0 & & 2^{L-1} & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 & \cdots & 0 & 2^{L-1} & 0 \\ 0 & 0 & 1 & 0 & 0 & 2 & & 0 & 0 & 2^{L-1} \end{bmatrix}^\top \\ \gamma(\mathbf{x}) = \begin{bmatrix} \sin (\mathbf{Px}) \\ \cos (\mathbf{Px}) \end{bmatrix} \end{equation}\]

이러한 reparameterization을 통해 IPE에 대한 closed-form을 유도할 수 있다. 변수의 선형 변환의 공분산이 변수 공분산의 선형 변환이라는 사실을 사용하여

\[\begin{equation} \textrm{Cov}[\mathbf{Ax}, \mathbf{By}] = \mathbf{A} \textrm{Cov}[\mathbf{x}, \mathbf{y}] \mathbf{B}^\top \end{equation}\]

원뿔 절두체 Gaussian의 평균과 공분산을 식별할 수 있다.

\[\begin{equation} \boldsymbol{\mu}_\gamma = \mathbf{P} \boldsymbol{\mu}, \quad \mathbf{\Sigma}_\gamma = \mathbf{P} \mathbf{\Sigma} \mathbf{P}^\top \end{equation}\]

IPE feature 생성의 마지막 단계는 위치의 사인 및 코사인으로 변조된 이 multivariate Gaussian에 대한 기대값을 계산하는 것이다. 이러한 기대값은 간단한 closed-form 표현이 있다.

\[\begin{aligned} E_{x \sim \mathcal{N}(\mu, \sigma^2)} [\sin(x)] &= \sin(\mu) \exp (-(1/2)\sigma^2) \\ E_{x \sim \mathcal{N}(\mu, \sigma^2)} [\cos(x)] &= \cos(\mu) \exp (-(1/2)\sigma^2) \end{aligned}\]

이 사인 또는 코사인의 기대값은 단순히 분산의 Gaussian function에 의해 감쇠된 평균의 사인 또는 코사인이다. 이를 통해 공분산 행렬의 diagonal과 평균의 사인 및 코사인 기대값으로 최종 IPE feature를 계산할 수 있다.

\[\begin{aligned} \gamma (\boldsymbol{\mu}, \mathbf{\Sigma}) &= \mathbb{E}_{\mathbf{x} \sim \mathcal{N}(\boldsymbol{\mu}_\gamma, \mathbf{\Sigma}_\gamma)} [\gamma (\mathbf{x})] \\ &= \begin{bmatrix} \sin(\boldsymbol{\mu}_r) \circ \exp (-(1/2) \textrm{diag} (\mathbf{\Sigma}_\gamma)) \\ \cos(\boldsymbol{\mu}_r) \circ \exp (-(1/2) \textrm{diag} (\mathbf{\Sigma}_\gamma)) \end{bmatrix} \end{aligned}\]

여기서 $\circ$는 element-wise multiplication이다. PE는 각 차원을 독립적으로 인코딩하기 때문에 이 인코딩 기대값은 $\gamma(x)$의 주변 분포에만 의존하고 공분산 행렬의 diagonal만 필요하다. \(\mathbf{\Sigma}_\gamma\)는 상대적으로 큰 크기로 인해 계산하는 데 엄청나게 비용이 많이 들기 때문에 \(\mathbf{\Sigma}_\gamma\)의 diagonal을 직접 계산한다.

\[\begin{equation} \textrm{diag} (\mathbf{\Sigma}_\gamma) = [\textrm{diag} (\mathbf{\Sigma}), 4 \textrm{diag} (\mathbf{\Sigma}), \cdots, 4^{L-1} \textrm{diag} (\mathbf{\Sigma})]^\top \end{equation}\]

이 벡터는 3D 위치 공분산 $\mathbf{\Sigma}$의 diagonal에 따라 달라지며 다음과 같이 계산할 수 있다.

\[\begin{equation} \textrm{diag} (\mathbf{\Sigma}) = \sigma_t^2 (\mathbf{d} \circ \mathbf{d}) + \sigma_r^2 \bigg( \mathbf{1} - \frac{\mathbf{d} \circ \mathbf{d}}{\| \mathbf{d} \|_2^2} \bigg) \end{equation}\]

이러한 diagonal을 직접 계산하는 경우 IPE feature는 대략 PE feature만큼의 비용이 든다.


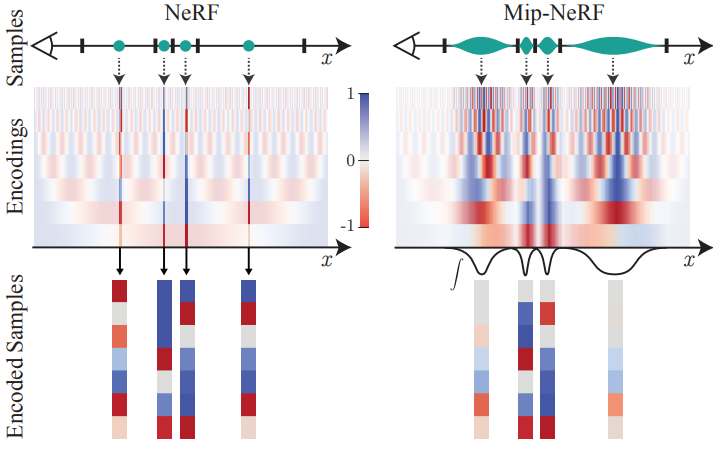
위 그림은 toy 1D 도메인에서 IPE feature와 PE feature 사이의 차이점을 시각화한 것이다. IPE feature는 직관적으로 작동한다. PE의 특정 주파수에 IPE feature를 구성하는 데 사용되는 간격의 너비보다 큰 주기가 있는 경우 해당 주파수의 인코딩은 영향을 받지 않는다. 그러나 주기가 간격보다 작은 경우 (이 경우 해당 간격의 PE가 반복적으로 진동함) 해당 주파수의 인코딩은 0을 향해 축소된다. 간단히 말해서, IPE는 간격에 걸쳐 일정한 주파수를 유지하고 간격에 따라 변하는 주파수를 부드럽게 제거하는 반면, PE는 수동으로 튜닝된 hyperparameter $L$까지 모든 주파수를 보존한다. 이러한 방식으로 각 사인과 코사인을 스케일링함으로써 IPE feature는 효과적으로 공간의 크기와 모양을 원활하게 인코딩하는 안티앨리어싱된 PE feature이다. 또한 IPE는 hyperparameter인 $L$을 효과적으로 제거한다. 즉, 매우 큰 값으로 간단히 설정한 다음 튜닝하지 않을 수 있다.

2. Architecture

Cone-tracing과 IPE feature 외에도 mip-NeRF는 NeRF와 유사하게 작동한다. 렌더링되는 각 픽셀에 대해 NeRF와 같이 광선 대신 원뿔이 캐스팅된다. 광선을 따라 $t_k$에 대해 $n$개의 값을 샘플링하는 대신 $t_k$에 대해 $n + 1$개의 값을 샘플링하고 $t_k$ 값의 각 인접한 쌍에 걸쳐 있는 간격에 대한 IPE feature를 계산한다. 이러한 IPE feature는 밀도 $\tau_k$와 색상 $c_k$를 생성하기 위해 MLP에 입력으로 전달된다. mip-NeRF에서의 렌더링은 아래 방정식을 따른다.

\[\begin{equation} C(r; \Theta, t) = \sum_k T_k (1 - \exp (- \tau_k (t_{k+1} - t_k))) c_k \\ \textrm{where} \; T_k = \exp \bigg( - \sum_{k^\prime < k} \tau_{k^\prime} (t_{k^\prime + 1} - t_{k^\prime}) \bigg) \end{equation}\]

NeRF는 두 개의 서로 다른 MLP (“coarse” MLP와 “fine” MLP)를 사용하는 계층적 샘플링 절차를 사용한다. NeRF의 PE feature는 MLP가 하나의 스케일에 대한 장면 모델만 학습할 수 있다는 것을 의미했기 때문에 이는 NeRF에서 필요했다. 그러나 원뿔 캐스팅과 IPE feature를 사용하면 입력 feature에 스케일을 명시적으로 인코딩할 수 있으므로 MLP가 장면의 멀티스케일 표현을 학습할 수 있다. 따라서 mip-NeRF는 계층적 샘플링 전략에서 반복적으로 쿼리하는 하나의 MLP (파라미터 $\Theta$)를 사용한다. 여기에는 여러 가지 이점이 있다. 모델 크기가 절반으로 줄어들고, 렌더링이 더 정확해지고, 샘플링이 더 효율적이며, 전체 알고리즘이 더 단순해진다. 최적화 문제는 다음과 같다.

\[\begin{equation} \min_\Theta \sum_{\mathbf{r} \in \mathcal{R}} (\lambda \| \mathbf{C}^\ast (\mathbf{r}) - \mathbf{C} (\mathbf{r}; \Theta, \mathbf{t}^c) \|_2^2 + \| \mathbf{C}^\ast (\mathbf{r}) - \mathbf{C} (\mathbf{r}; \Theta, \mathbf{t}^f) \|_2^2 ) \end{equation}\]

하나의 MLP가 있기 때문에 coarse loss는 fine loss와 균형을 이루어야 하며 이는 hyperparameter $\lambda = 0.1$을 사용하여 달성된다. Coarse 샘플 $\mathbf{t}^c$는 계층화된 샘플링으로 생성되고, fine 샘플 $\mathbf{t}^f$는 역변환 샘플링을 사용하여 알파 합성 가중치 $\mathbf{w}$에서 샘플링된다. Fine MLP에 64개의 coarse 샘플과 128개의 fine 샘플의 정렬된 합집합이 제공되는 NeRF와 달리 mip-NeRF에서는 단순히 coarse 모델에 대해 128개의 샘플과 fine 모델에서 128개의 샘플을 샘플링한다. $\mathbf{t}^f$를 샘플링하기 전에 가중치 $\mathbf{w}$를 다음과 같이 약간 수정한다.

\[\begin{equation} w_k^\prime = \frac{1}{2} (\max (w_{k-1}, w_k) + \max (w_k, w_{k+1})) + \alpha \end{equation}\]

2-tap max filter와 2-tap blur filter (blurpool)로 $\mathbf{w}$를 필터링하여 $\mathbf{w}$에 넓고 부드러운 upper envelope를 생성한다. Hyperparameter $\alpha$는 합계가 1로 다시 정규화되기 전에 해당 envelope에 추가된다. 이는 일부 샘플이 빈 공간 영역에서도 그려지도록 보장한다 ($\alpha = 0.01$).

Results

Multiscale Blender Dataset

다음은 NeRF와 멀티스케일 Blender 데이터셋에서 정량적으로 비교한 표이다.


다음은 멀티스케일 Blender 데이터셋에 대한 결과를 시각화한 것이다.

Blender Dataset

다음은 NeRF와 단일 스케일 Blender 데이터셋에서 정량적으로 비교한 표이다.


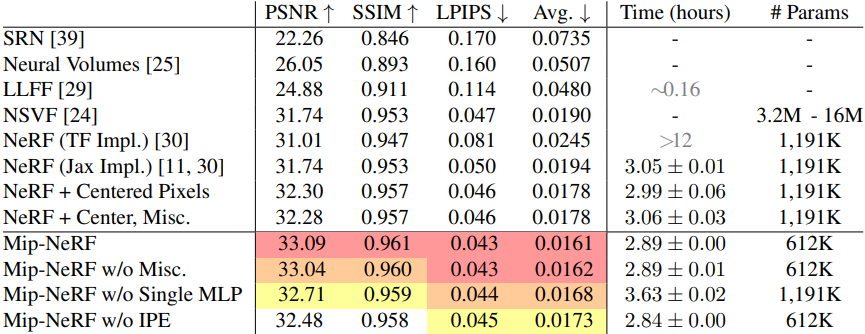
다음은 단일 스케일 Blender 데이터셋에 대한 결과를 시각화한 것이다.

Supersampling

다음은 supersampling(SS)된 mip-NeRF와 개선된 NeRF를 비교한 표이다.

You may also enjoy