Diffusion은 신이고 GPT는 무적이다

arXiv 2024. [Paper]
Jiameng Li, Yue Shi, Jiezhang Cao, Bingbing Ni, Wenjun Zhang, Kai Zhang, Luc Van Gool
University of Stuttgart | ETH Zurich | Shanghai Jiaotong University | Nanjing University | Sofia University
12 Aug 2024

Introduction


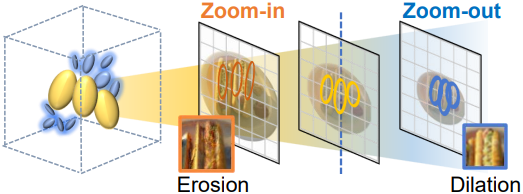
3D Gaussian Splatting (3DGS)는 확대 또는 축소할 때 심각한 앨리어싱 또는 흐릿함이 발생하여 사용자 경험이 저하된다. 일반적으로 단일 스케일 이미지에서 학습된 3DGS는 관찰 거리, 이미지 해상도, 카메라 초점 거리의 변경으로 샘플링 속도가 달라지는 것에 민감하다. Zoom-in하면 dilation이 발생하고 zoom-out하면 erosion이 발생하며, 두 경우 모두 앨리어싱이라 부른다.


학습된 스케일과 다른 스케일에서의 품질 저하는 학습된 Gaussian과 샘플링 속도 간의 불일치로 인해 발생한다. 3D Gaussian은 이미지 평면에 projection되고 rasterization 전에 2D dilation filter를 거쳐 shrinkage bias를 부드럽게 한다. 그러나 변형 불가능한 Gaussian과 0.3으로 고정된 dilation factor는 다양한 설정과 완벽하게 일치하지 않는다.

Zoom-in할 때 화면 공간의 축소된 Gaussian이 적절하게 매끄럽지 않아 화면에 바늘과 같은 스파이크가 생긴다. 더 나쁜 것은 zoom-in 시 픽셀 그리드가 더 세밀해져서 Gaussian이 splatting되지 않은 빈 영역이 생겨 구조가 누락된다. 반대로 zoom-out하면 너무 많은 Gaussian이 하나의 픽셀에 기여하기 때문에 밝기와 두께가 지나치게 커진다.

본 논문에서는 이 문제를 해결하는 3DGS를 위한 새로운 스케일 적응형 최적화 방법을 제안하였다. 구체적으로, self-supervised 방식으로 스케일별 정보를 제공하기 위해 mipmap과 유사한 pseudo-GT를 구성한다. 테스트 시 새로운 뷰에서 한 번 생성되고 미리 계산된 mipmap을 스케일별 pseudo-GT로 변경한다. Mipmap으로 Gaussian을 변형하기 위해 scale-aware guidance loss를 도입한다. 이러한 self-supervised 최적화를 통해 임의의 스케일에 대한 렌더링에 적합해진다.

Motivation

Shrinkage bias와 2D dilation

실제로 3D Gaussian은 shrinkage bias가이 있는 픽셀 색상을 계산하기 위해 잘린다. 극심한 축소는 렌더링에서 바늘과 같은 스파이크가 된다. 또한 1픽셀 미만의 사소한 기여를 하는 작은 Gaussian은 최적화하기 어렵다. 따라서 rasterization 전에 2D dilation 연산을 설계하여 shrinkage bias를 줄인다.

\[\begin{equation} G_k^\textrm{2D} (x) = \exp ( -\frac{1}{2} (x - \mu_k)^\top (\Sigma_k^{2D} + sI)^{-1} (x - \mu_k)) \end{equation}\]

여기서 dilation factor $s$는 0.3으로 설정된다. Dilation 연산은 low-pass filter로 작동하여 shrinkage bias를 부드럽게 하여 충실한 렌더링을 달성한다.

기본 스케일에서 유망한 NVS 결과에도 불구하고 zoom-in 및 zoom-out 렌더링은 일반화에 두 가지 과제를 안겨준다.

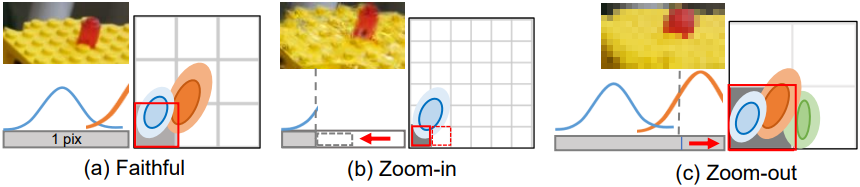
다양한 샘플링 속도

픽셀 셰이딩 중에 픽셀 그리드는 현재 샘플링 속도에 따라 할당된다. 그런 다음 한 픽셀에서 겹치는 Gaussian은 shrinkage bias와 함께 누적된다. 샘플링 속도가 변경되면 다양한 shrinkage bias로 인해 누적 중에 혼란이 발생한다. 위 그림은 여러 샘플링 속도와 1D로 축소된 Gaussian 신호를 보여준다. 학습된 Gaussian은 (a) 기본 스케일에서 두 신호를 샘플링하는 반면, (b) zoom-in 픽셀은 파란색 신호만 캡처하고 (c) zoom-out 픽셀은 과도한 기여로 인해 주황색 신호를 누적한다.

일정한 dilation

셰이딩 중 픽셀 범위는 projection된 Gaussian과 dilation 연산에 의해 공동으로 결정된다. 3DGS의 2D dilation 연산은 한 픽셀 (회색)보다 작은 Gaussian (파란색)을 증폭하도록 설계되었다. 그러나 zoom-in 시 동일한 dilation을 유지하면 감소된 픽셀 범위에 적합하지 않아 얇은 구조와 splat이 없는 빈 영역이 발생한다. 반대로, zoom-out 시 동일한 dilation을 유지하면 범위가 지나치게 넓고 구조가 두꺼워져 렌더링 효율성도 떨어진다. 위 그림의 (c)에서 녹색 Gaussian은 회색 픽셀에 포함되지 않아야 했지만, dilation으로 인해 픽셀 셰이딩에 포함된다.

Method

1. Mipmap-like Pseudo-GT

시간이 많이 걸리는 멀티스케일 학습을 수행하는 대신, mipmap과 유사한 pseudo-GT를 사용하여 스케일 적응형 Gaussian을 최적화한다. 3DGS의 NVS 용량을 고려하여, 먼저 기본 스케일($\times 1$)에서 기본 Gaussian들을 새로운 뷰로 splat시킨다. 이 뷰는 저하가 없다. 그런 다음, mipmap resizing function $r(x)$를 사용하여 새로운 스케일 pseudo-GT를 구성한다.

Zoom-in 적응의 경우, 새로운 뷰에서 렌더링된 이미지는 SwinIR과 같은 super-resolution 방법을 사용하여 $\times N$으로 업샘플링된다. 마찬가지로, zoom-out을 위한 스케일별 mipmap을 생성하기 위해, 렌더링된 이미지는 원래 해상도의 $\times 1/N$으로 다운샘플링된다. 확장된 픽셀에 대한 디테일을 생성해야 하는 zoom-in 프로세스와 비교할 때, 다운샘플링 단계는 텍스처 저하가 적다. 따라서 단순히 $r(x)$로 bilinear interpolation을 채택하여 LR mipmap을 생성한다.

2. Scale-Adaptive 3D Gaussians

3DGS는 Gaussian을 알파-블렌딩된 2D Gaussian들로 이미지 공간에 projection하여 픽셀 색상을 축적한다. 3D shrinkage bias와 2D dilation 복원은 학습 스케일에 맞도록 협력한다. 그러나 서로 다른 공간에서 발생하는 이 두 연산은 독립적으로 작동한다. 이 공간 차이는 멀티스케일 렌더링에서 앞서 말한 두 가지 문제를 발생시킨다. 다양한 샘플링 속도가 일정한 dilation의 제어 범위를 초과하여 앨리어싱 결과를 초래하기 때문이다.

이 차이를 메우기 위해 기본 Gaussian $\mathbf{G}$에서 스케일별 mipmap $r(\hat{x})$를 생성한다. 그런 다음 렌더링된 이미지 $x$와 스케일별 mipmap $r(\hat{x})$ 사이의 photometric loss로 $\mathbf{G}$를 최적화된 Gaussian \(\mathbf{G}^\textrm{opt}\)로 변형한다. ($\beta$ : learning rate)

\[\begin{equation} \mathbf{G}^\textrm{opt} = \mathbf{G} - \beta \nabla L (x, r(\hat{x})) \end{equation}\]

이 방법은 일정한 dilation으로 인한 문제를 완화하기 위해 필터를 도입하는 대신 새로운 샘플링 속도를 직접 알려주기 때문에 본질적으로 앨리어싱을 해결한다. 스케일 적응형 Gaussian은 변형 가능한 속성과 분포를 활용하여 모든 스케일 렌더링에 맞춘다. Test-time 적응 방법이기 때문에 광범위한 커버리지의 inference에 대해 3D Gaussian과 2D 픽셀 커버리지 간의 스케일 일관성을 유지할 수 있다.

3. Optimization


먼저 기본 Gaussian $\mathbf{G}$를 사용하여 새로운 뷰 $\hat{x}$를 생성한다. 그런 다음, $\hat{x}$는 mipmap 함수를 통해 $r(\hat{x})$로 업샘플링되거나 다운샘플링되어 pseudo-GT 역할을 한다. Scale-aware guidance loss는 다음과 같이 정의된다.

\[\begin{equation} L(x, r(\hat{x})) = \| x - r(\hat{x}) \|^2 \end{equation}\]

$\mathbf{G}$에서 \(\mathbf{G}^\textrm{opt}\)로의 변형은 1,000 iteration 이내에 완료된다.

Algorithm 1에서 최적화된 Gaussian \(\mathbf{G}^\textrm{opt}\)의 개수 $K^\textrm{opt}$는 이전 개수 $K$보다 작다. 3DGS의 density control은 최적화 프로세스 중간에 중단되어 많은 낮은 불투명도의 Gaussian이 사소한 기여를 하게 된다. 이와 대조적으로, 보다 컴팩트한 표현을 위해 전체 프로세스 동안 pruning을 활성화한다. 이에 따른 저장 공간 감소는 감소된 공간 해상도로 인해 표현할 Gaussian이 더 적게 필요한 zoom-out 상황에서 더 분명하다. 게다가, 처음부터 학습하는 것과 비교했을 때 단지 3%의 iteration만 필요하며, 원래 파이프라인이나 새로운 hyper-parameter에 대한 간섭이 없으므로 Scaffold-GS와 같은 후속 연구들과도 호환된다.

Experiments

  • 구현 디테일
    • GPU: A100 1개
    • hyper-parameter는 3DGS와 동일

1. Comparisons with State-of-the-Art

다음은 NeRF Synthetic 데이터셋에 대한 결과이다.


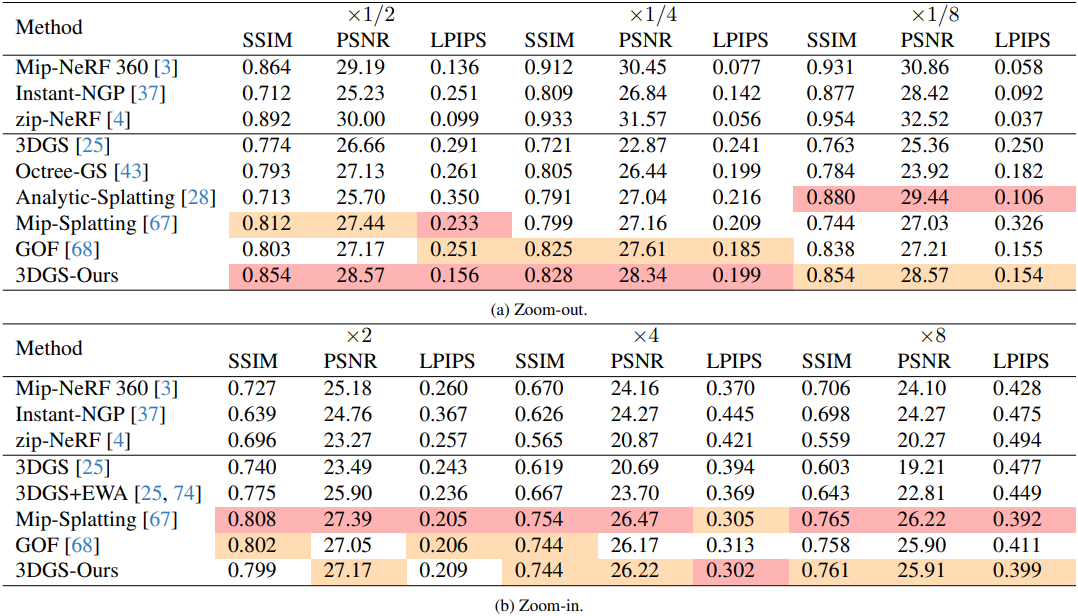
다음은 Mip-NeRF 360 데이터셋에 대한 결과이다.

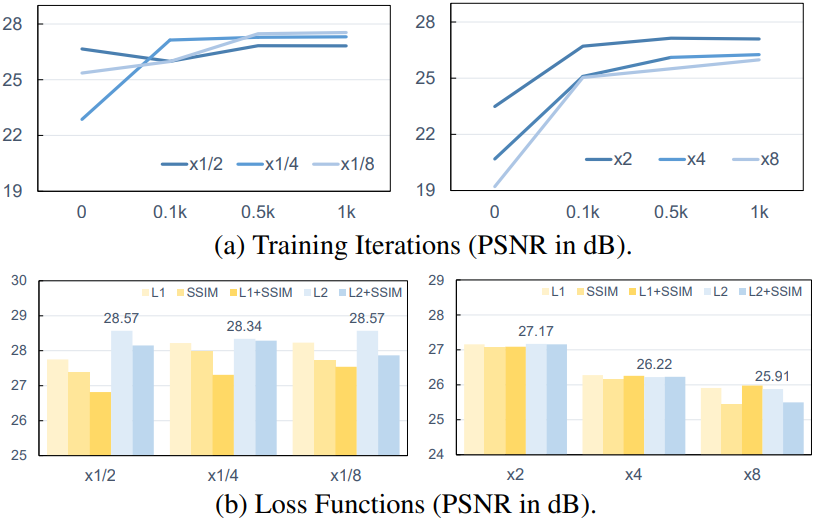
2. Ablation Study

다음은 (a) 학습 iteration 수와 (b) loss function에 대한 ablation 결과이다.


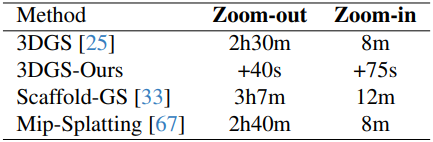
다음은 학습 시간을 비교한 표이다. (Mip-NeRF 360 - bicycle)


다음은 최적화 뷰에 따른 렌더링 품질을 비교한 표이다. (Mip-NeRF 360 - bicycle)

3. Further Study

다음은 $\times 1/8$로 학습된 bicycle 장면에 대한 선택적 렌더링 결과를 비교한 것이다. (*: 불투명도 > 0.01로 선택적 렌더링)


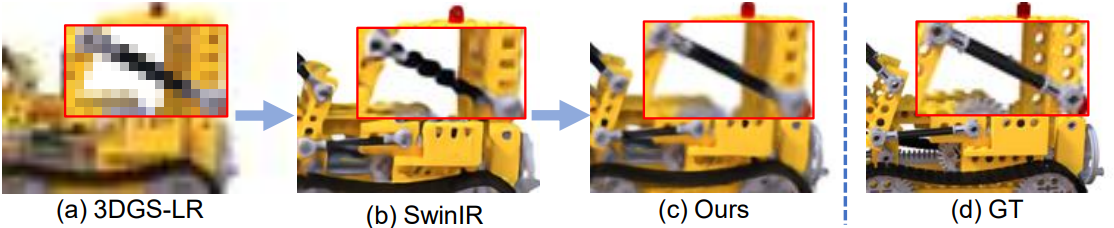
다음은 장면 레벨의 fine-tuning 없이 SwinIR로 각 이미지에 대해 독립적으로 mipmap을 구성하고 학습시킨 결과와 Mipmap-GS를 비교한 것이다.


다음은 동적 장면에 Mipmap-GS를 적용한 예시이다.

You may also enjoy