[논문리뷰] Efficient Diffusion Training via Min-SNR Weighting Strategy
ICCV 2023. [Paper] [Github]
Tiankai Hang, Shuyang Gu, Chen Li, Jianmin Bao, Dong Chen, Han Hu, Xin Geng, Baining Guo
Southeast University | Microsoft Research Asia | Xi’an Jiaotong University
16 Mar 2023
Introduction
최근 몇 년 동안 DDPM은 복잡한 분포를 모델링할 수 있는 놀라운 능력으로 인해 유망한 새로운 유형의 심층 생성 모델로 부상했다. 이전의 GAN과 비교하여 diffusion model은 다양한 modality의 생성 task 범위에서 우수한 성능을 입증했다. 현재 DDPM의 주요 제한 사항은 느린 수렴 속도로, 학습에 상당한 양의 GPU 시간이 필요하다. 이는 이러한 모델을 효과적으로 실험하려는 연구자에게 상당한 도전 과제이다.
본 논문에서는 먼저 이 문제에 대한 철저한 조사를 수행하여 느린 수렴 속도가 학습 중 서로 다른 timestep에 대한 충돌하는 최적화 방향에서 발생할 가능성이 있음을 밝혔다. 특정 noise 레벨에 대한 denoising function을 전용으로 최적화하면 다른 noise 레벨에 대한 재구성 성능에도 해를 끼칠 수 있다. 현재 DDPM이 다양한 noise 레벨에 대해 공유 모델 가중치를 사용한다는 점을 감안할 때 이러한 noise timestep의 균형을 신중하게 고려하지 않으면 충돌하는 가중치 기울기가 전체 수렴 속도를 방해할 것이다.
본 논문은 이 문제를 해결하기 위해 Min-SNR-$\gamma$ loss 가중치 전략을 제안한다. 이 전략은 각 timestep의 denoising process를 개별 task로 취급하므로 diffusion 학습은 multi-task 학습 문제로 간주될 수 있다. 다양한 task의 균형을 맞추기 위해 각 task의 난이도에 따라 loss 가중치를 할당한다. 구체적으로, 기울기 충돌 문제를 완화하기 위해 loss 가중치로 클램핑된 signal-to-noise ratio (SNR)을 채택한다. 이 새로운 가중치 전략을 사용하여 다양한 timestep을 구성함으로써 diffusion 학습 프로세스는 이전 접근 방식보다 훨씬 빠르게 수렴할 수 있다.
일반적인 multi-task 학습 방법은 기울기에 따라 각 task의 loss 가중치를 조정하여 task 간의 충돌을 완화하려고 한다. 하나의 고전적인 접근 방식인 Pareto 최적화는 모든 task를 개선하기 위해 경사 하강 방향을 찾는 것을 목표로 한다. 그러나 이러한 접근 방식은 세 가지 측면에서 Min-SNR-$\gamma$ 가중치 전략과 다르다.
- 희소성: 일반적인 multi-task 학습 분야의 대부분의 이전 연구는 task 수가 수천에 달할 수 있는 diffusion 학습과 달리 적은 수의 task가 있는 시나리오에 중점을 두었다. Diffusion 학습의 Pareto 최적 해는 대부분의 timestep의 loss 가중치를 0으로 설정하는 경향이 있다. 이러한 방식으로 많은 timestep이 학습 없이 남게 되어 전체 denoising process에 해를 끼친다.
- 불안정성: 각 iteration의 각 timestep에 대해 계산된 기울기는 각 timestep에 대한 제한된 수의 샘플로 인해 noisy한 경우가 많다. 이는 Pareto 최적 해의 정확한 계산을 방해한다.
- 비효율성: Pareto 최적 해의 계산은 시간이 많이 걸리므로 전체 학습 속도가 상당히 느려진다.
Min-SNR-$\gamma$ 전략은 원래 Pareto 최적화에서와 같이 각 iteration에 대한 런타임 적응 loss 가중치 대신 미리 정의된 글로벌 step별 loss 가중치 설정이므로 희소성 문제를 피할 수 있다. 또한 글로벌 loss 가중 전략은 noisy한 기울기 계산과 시간 소모적인 Pareto 최적화 프로세스의 필요성을 제거하여 보다 효율적이고 안정적이다. 차선이지만 글로벌 전략도 거의 효과적일 수 있다.
- 각 denoising task의 최적화 역학은 개별 샘플을 너무 많이 고려할 필요 없이 주로 task의 noise 레벨에 의해 형성된다.
- 적당한 수의 iteration 후에 대부분의 후속 학습 프로세스의 기울기가 더 안정적이 되므로 고정 가중치 전략으로 근사화할 수 있다.
Method
1. Diffusion Training as Multi-Task Learning
파라미터의 수를 줄이기 위해 이전 연구는 종종 모든 step에서 denoising model의 파라미터를 공유한다. 그러나 step마다 요구 사항이 크게 다를 수 있다는 점을 염두에 두어야 한다. Diffusion model의 각 step에서 denoising의 강도는 다양하다. 예를 들어 더 쉬운 denoising task ($t \rightarrow 0$인 경우)는 더 낮은 denoising loss를 달성하기 위해 입력의 간단한 재구성이 필요할 수 있다. 불행하게도 이 전략은 noise가 많은 task ($t \rightarrow T$인 경우)에는 적합하지 않다. 따라서 서로 다른 timestep 간의 상관 관계를 분석하는 것이 매우 중요하다.
저자들은 이와 관련하여 간단한 실험을 수행했다. Denoising process를 여러 개의 별도 bin으로 클러스터링하는 것으로 시작한다. 그런 다음 각 bin에서 timestep을 샘플링하여 diffusion model을 fine-tuning한다. 마지막으로 다른 bin의 loss에 어떤 영향을 미쳤는지 살펴봄으로써 효율성을 평가하였다.
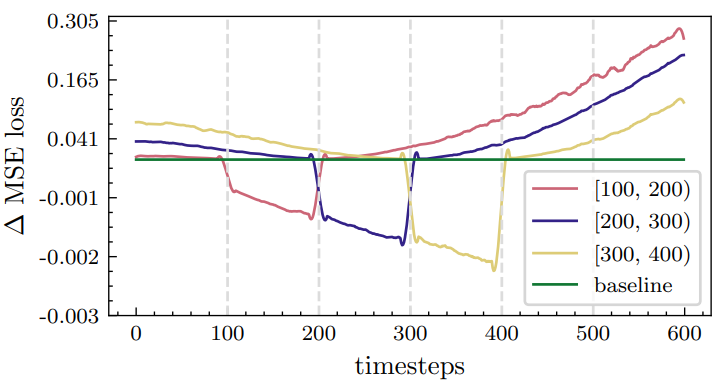
위 그림에서 볼 수 있듯이 특정 step을 fine-tuning하면 주변 step에 도움이 된다는 것을 관찰할 수 있다. 그러나 멀리 떨어져 있는 다른 step에는 종종 불리하다. 이는 모든 timestep에 동시에 혜택을 주는 보다 효율적인 솔루션을 찾을 수 있는지 여부를 고려하도록 영감을 준다.
저자들은 multi-task 학습의 관점에서 목적 함수를 재구성했다. DDPM의 학습 프로세스에는 $T$개의 서로 다른 task가 포함되며 각 task는 개별 timestep을 나타낸다. 모델 파라미터를 $\theta$로 표시하고 해당 학습 loss는 $\mathcal{L}^t (\theta)$로 표시한다. 다음을 만족하는 업데이트 방향 $\delta \ne 0$을 찾는 것이 목표이다.
\[\begin{equation} \mathcal{L}^t (\theta + \delta) \le \mathcal{L}^t (\theta), \quad \forall \in \{1, \cdots, T\} \end{equation}\]1차 테일러 전개는 다음과 같다.
\[\begin{equation} \mathcal{L}^t (\theta + \delta) \approx \mathcal{L}^t (\theta) + \langle \delta, \nabla_\theta \mathcal{L}^t (\theta) \rangle \end{equation}\]따라서 이상적인 업데이트 방향은 다음과 같다.
\[\begin{equation} \langle \delta, \nabla_\theta \mathcal{L}^t (\theta) \rangle \le 0, \quad \forall \in \{1, \cdots, T\} \end{equation}\]2. Pareto optimality of diffusion models
최적화 문제
\[\begin{equation} \min_{w^t} \bigg\{ \| \sum_{t=1}^T w^t \nabla_\theta \mathcal{L}^t (\theta) \|^2 \; \vert \; \sum_{t=1}^T w^t = 1, \; w^t \ge 0 \bigg\} \end{equation}\]의 해인 $w_t$에 대하여 업데이트 방향
\[\begin{equation} \delta^\ast = - \sum_{t=1}^T w_t \nabla_\theta \mathcal{L}^t (\theta) \end{equation}\]를 고려하자. 만일 \(\langle \delta, \nabla_\theta \mathcal{L}^t (\theta) \rangle \le 0\)에 대한 최적 해가 존재하면 $\delta^\ast$가 이를 만족해야 한다. 그렇지 않으면 다른 task의 loss 감소에 대한 대가로 특정 task를 희생해야 함을 의미한다. 즉, Pareto Stationary에 도달했으며 학습이 수렴되었다.
Diffusion model은 이미지를 생성할 때 모든 timestep을 거쳐야 하기 학습 중에 timestep을 무시해서는 안 된다. 따라서 loss 가중치가 지나치게 작아지는 것을 방지하기 위해 정규화 항이 포함되어야 한다. 최적화 목적 함수는 다음과 같다.
\[\begin{equation} \min_{w_t} \bigg\{ \| \sum_{t=1}^T w_t \nabla_\theta \mathcal{L}^t (\theta) \|_2^2 + \lambda \sum_{t=1}^T \| w_t \|_2^2 \bigg\} \end{equation}\]여기서 $\lambda$는 정규화 강도를 조절한다.
위 식을 풀기 위해 Frank-Wolfe 알고리즘을 활용하여 반복적인 최적화를 통해 가중치 \(\{w_t\}\)를 얻는다. 또 다른 접근 방식은 Unconstrained Gradient Descent (UGD)를 채택하는 것이다. 구체적으로 $w_t$를 $\beta_t$로 reparameterize한다.
\[\begin{equation} w_t = \frac{e^{\beta_t}}{Z}, \quad Z = \sum_t e^{\beta_t}, \quad \beta_t \in \mathbb{R} \end{equation}\]Gradient descent을 사용하여 각 항을 독립적으로 최적화하면 다음과 같다.
\[\begin{equation} \min_{\beta_t} \frac{1}{Z^2} \| \sum_{t=1}^T e^{\beta_t} \nabla_\theta \mathcal{L}^t (\theta) \|_2^2 + \frac{\lambda}{Z^2} \sum_{t=1}^T \| e^{\beta_t} \|_2^2 \end{equation}\]그러나 Frank-Wolfe 알고리즘을 활용하든 UGD 알고리즘을 활용하든 두 가지 단점이 있다.
- 비효율성: 이 두 가지 방법 모두 각 학습 iteration마다 추가 최적화가 필요하므로 학습 비용이 크게 증가한다.
- 불안정성: 실제로 기울기 항 \(\nabla_\theta \mathcal{L}^t (\theta)\)를 계산하기 위해 제한된 수의 샘플을 사용하면 최적화 결과가 불안정하다. (아래 그래프 참조)

즉, 각 denoising task에 대한 loss 가중치는 학습 중에 크게 달라지므로 전체 diffusion 학습이 비효율적이다.
3. Min-SNR-$\gamma$ Loss Weight Strategy
각 iteration에서 반복적인 최적화로 인한 비효율성과 불안정성을 피하기 위해 한 가지 가능한 시도는 고정 loss 가중치 전략을 채택하는 것이다.
Noise가 없는 상태 $x_0$를 예측하기 위해 네트워크가 다시 parameterize되었다고 가정한다. 그러나 서로 다른 예측 목적 함수가 서로 변환될 수 있다는 점은 주목할 가치가 있다. 다음과 같은 대체 학습 loss 가중치를 고려한다.
- Constant weighting: $w_t = 1$
- SNR weighting: $w_t = \textrm{SNR} (t) = \alpha_t^2 / \sigma_t^2$. 가장 널리 사용되는 가중치 전략이다. 예측 대상이 noise일 때 constant weighting 전략과 수치적으로 동일하다.
- Max-SNR-$\gamma$ weighting: \(w_t = \max \{\textrm{SNR} (t), \gamma\}\). 이러한 수정은 SNR step이 0인 가중치 0을 피하기 위해 처음으로 제안되었다. 기본 설정으로 $\gamma = 1$을 설정한다. 그러나 가중치는 여전히 작은 noise 레벨에 집중된다.
- Min-SNR-$\gamma$ weighting: \(w_t = \min \{\textrm{SNR} (t), \gamma\}\). 저자들은 모델이 작은 noise 레벨에 너무 집중하는 것을 피하기 위해 이 가중치 전략을 제안하였다.
- UGD optimization weighting: 각 timestep에서 $w_t$는 UGD로 최적화된다. 이전 설정과 비교하여 이 전략은 학습 중에 변경된다.
저자들은 먼저 이러한 가중치 전략을 최적화 목적 함수에 결합하여 Pareto 최적 상태에 접근하는지 여부를 검증하였다.

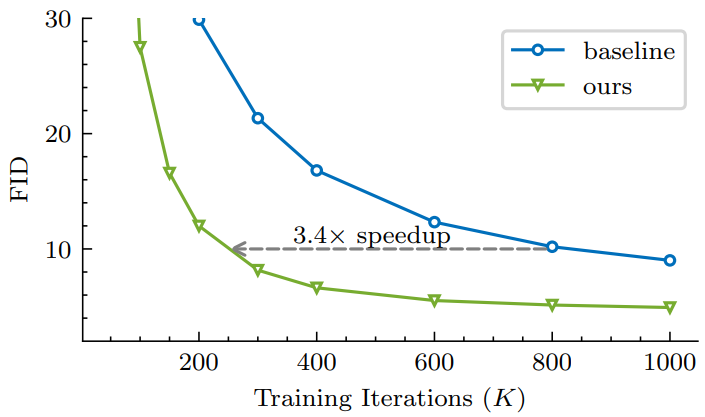
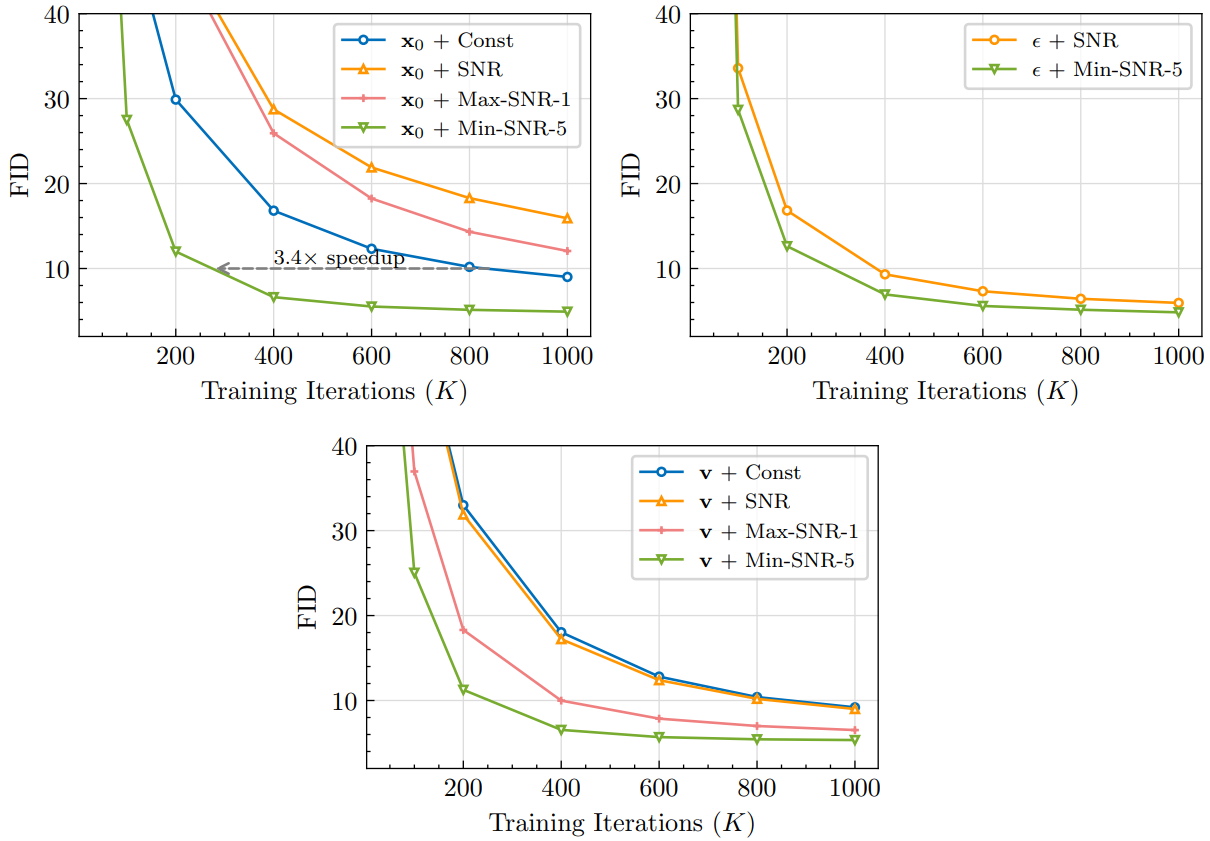
위 그림에서 볼 수 있듯이 UGD 최적화 가중치 전략은 최적화 목적 함수에서 가장 낮은 값을 얻을 수 있다. 또한 Min-SNR-$\gamma$ 가중 전략은 최적에 가장 가깝고 서로 다른 timestep을 동시에 최적화하는 속성이 있음을 보여준다. 본 논문의 접근 방식은 더 빠른 수렴과 강력한 성능을 달성하는 것을 목표로 한다.
Experiments
- 데이터셋
- CelebA: 140$\times$140 centor crop 후 64$\times$64로 resize
- ImageNet: 클래스 조건부 이미지 생성. 64$\times$64, 256$\times$256
- 학습 디테일
- 저해상도 이미지 생성의 경우 ADM을 따라 픽셀 레벨에서 직접 학습
- 고해상도 이미지 생성의 경우 LDM을 따라 latent 분포를 모델링. Stable Diffusion의 VQ-VAE 사용
- backbone으로 ViT와 UNet 모두 사용
- timestep 수: $T = 1000$
- optimizer: AdamW
- CelebA의 경우 50만 iteration, batch size는 128, learning rate는 $10^{-4}$ (5천 iteration 동안 linear warmup)
- ImageNet의 경우 batch size는 1024 ($64^2$) / 256 ($256^2$), learning rate는 $10^{-4}$로 고정
1. Analysis of the Proposed Min-SNR-$\gamma$
다음은 $x_0,$ $\epsilon$, $v$를 예측할 때 다양한 loss 가중 디자인을 비교한 그래프이다.
다음은 다양한 timestep에서 가중되지 않은 loss를 나타낸 그래프이다.
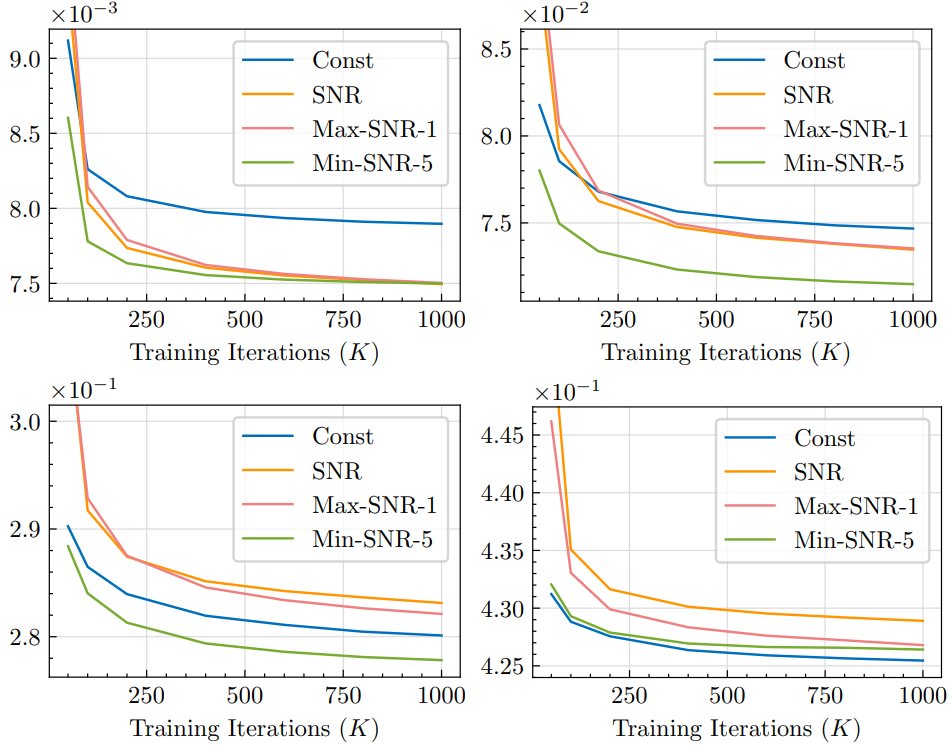
다음은 ImageNet 256$\times$256에서 다양한 가중 전략의 생성 결과를 비교한 것이다.

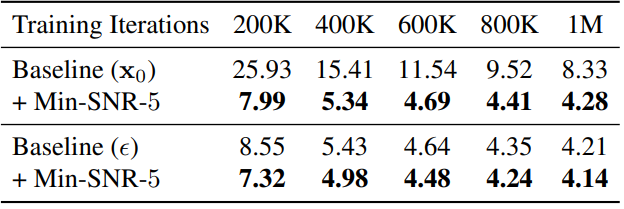
다음은 UNet backbone에 대한 ablation study 결과이다.
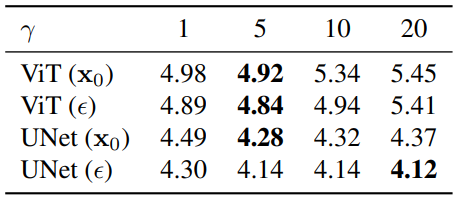
다음은 $\gamma$에 대한 ablation study 결과이다.
2. Comparison with state-of-the-art Methods
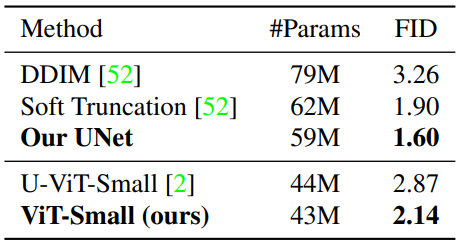
다음은 CelebA 64$\times$64에서의 unconditional한 이미지 생성 결과를 비교한 표이다.
다음은 ImageNet 64$\times$64에서의 클래스 조건부 이미지 생성 결과를 비교한 표이다.

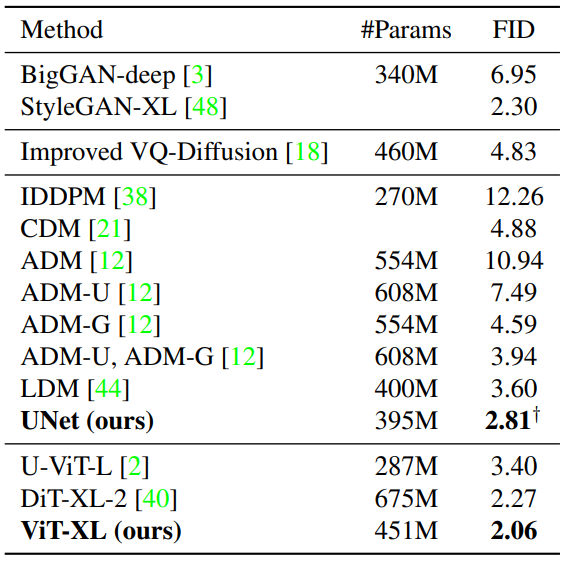
다음은 ImageNet 256$\times$256에서의 클래스 조건부 이미지 생성 결과를 비교한 표이다.