[논문리뷰] MeshSplatting: Differentiable Rendering with Opaque Meshes

arXiv 2025. [Paper] [Page] [Github]
Jan Held, Sanghyun Son, Renaud Vandeghen, Daniel Rebain, Matheus Gadelha, Yi Zhou, Anthony Cioppa, Ming C. Lin, Marc Van Droogenbroeck, Andrea Tagliasacchi
University of Liège | Simon Fraser University | University of Maryland | University of British Columbia | University of Toronto | Adobe Research
7 Dec 2025

Introduction

최근 Triangle Splatting은 볼륨 렌더링을 통해 삼각형을 최적화하여 3DGS의 Gaussian을 삼각형으로 대체하는 방법을 제안했다. 그러나 삼각형을 게임 엔진에서 렌더링할 경우, 게임 엔진이 삼각형을 불투명하게 가정하기 때문에 시각적 품질이 눈에 띄게 저하된다. 또한, 물리 기반 시뮬레이션에 종종 필요한 연결된 다각형 메쉬가 아닌, 삼각형들이 뒤섞인 형태를 이룬다.

본 논문에서는 앞서 언급한 모든 한계를 해결하기 위해 MeshSplatting을 소개한다. MeshSplatting은 현재 SOTA 방법보다 2배 빠른 학습 속도를 유지하면서 시각적 품질을 보존하는 메쉬 기반 장면 표현의 end-to-end 최적화를 제공한다. 제한된 Delaunay triangulation으로 traingle soup에서 연결된 메쉬를 생성한다. 삼각형들은 자연스럽게 서로 연결되며, vertex에 저장된 값들은 각 삼각형에 걸쳐 부드럽게 interpolation된다. 최적화 과정은 삼각형이 불투명해야 한다는 점을 고려하여 게임 엔진에서 고품질 렌더링을 직접 구현할 수 있도록 하였다. 이를 통해 depth buffer나 occlusion culling과 같은 기존 기술을 활용할 수 있다.

MeshSplatting은 기존의 메쉬 기반 novel view synthesis 방식보다 더 높은 시각적 충실도를 달성하고 더 세밀한 기하학적 디테일을 포착한다. 또한, MeshSplatting은 메쉬를 end-to-end로 재구성하여 메쉬 추출 과정 없이 연결되고 불투명하며 색상이 있는 삼각형 메쉬를 직접 생성하는 최초의 방법이다. MeshSplatting의 표현 방식은 게임 엔진에 직접 가져올 수 있어 다양한 응용 분야에 활용될 수 있다.

Method

1. Background

Triangle Splatting에서 각 삼각형 \(\textbf{T}_m\)은 세 개의 vertex \(\textbf{v}_i \in \mathbb{R}^3\), 색상 \(\textbf{c}_m\), smoothness 파라미터 \(\sigma_m\), 불투명도 $o_m$으로 정의된다. Rasterization은 핀홀 카메라 모델을 사용하여 삼각형 \(\textbf{T}_m\)의 각 vertex \(\textbf{v}_i\)를 이미지 평면에 projection하는 것으로 시작된다. 삼각형이 픽셀 $\textbf{p}$에 미치는 영향을 파악하고 splatting 과정을 미분 가능하게 하기 위해 이미지 공간에서 2D 삼각형의 SDF $\phi$는 다음과 같이 정의된다.

\[\begin{equation} \phi (\textbf{p}) = \max_{i \in \{1, 2, 3\}} (\textbf{n}_i \cdot \textbf{p} + d_i) \end{equation}\]

(\(\textbf{n}_i\)는 삼각형 바깥쪽을 향하는 삼각형 edge의 unit normal 벡터, $d_i$는 삼각형이 함수 $\phi$의 zero-level set으로 주어지도록 하는 offset)

따라서 SDF $\phi$는 삼각형 바깥쪽에서 양수 값을, 안쪽에서 음수 값을 가지며 경계에서는 0이다. Window function $I$는 다음과 같이 정의된다.

\[\begin{equation} I(\textbf{p}) = \left( \textrm{ReLU}\left( \frac{\phi (\textbf{p})}{\phi (\textbf{s})} \right) \right)^\sigma \end{equation}\]

($\textbf{s} \in \mathbb{R}^2$는 projection된 삼각형의 내심)

$I$는 삼각형 내심에서 1, 경계에서 0, 삼각형 외부에서 0이 된다. $\sigma$는 삼각형의 내심과 경계 사이의 전환을 제어하는 smoothness 파라미터이다. $\sigma \rightarrow 0$일 때 채워진 삼각형으로 수렴하는 반면, $\sigma$ 값이 클수록 경계에서 0에서 중심으로 갈수록 1로 점진적으로 증가하는 부드러운 window function이 생성된다.

이 삼각형 parameterization에는 두 가지 주요 한계가 있다.

1. 삼각형은 vertex를 공유하지 않고 서로 분리된 상태로 유지된다.
2. $\sigma$와 $o$를 독립적인 파라미터로 취급하기 때문에 학습 후 완전히 불투명해질 수 없다.

2. Vertex-sharing triangle representation

MeshSplatting에서는 메쉬 vertex들을 다음과 같이 정의한다.

\[\begin{equation} \mathcal{V} = \{\textbf{v}_i \in \mathbb{R}^3 \; \vert \; i = 1, \ldots, N\}, \quad \textbf{v}_i = (x_i, y_i, z_i, c_i, o_i) \end{equation}\]

\((x_i, y_i, z_i) \in \mathbb{R}^3\)은 vertex의 3D 위치, $c_i \in \mathbb{R}^3$는 vertex의 색상, $o_i \in [0, 1]$은 vertex의 불투명도를 나타낸다. 삼각형은 세 개의 vertex로 이루어진 \(\textbf{T}_m = \{v_i, v_j, v_k\}\)로 정의되며, 불투명도는 \(o_{\textbf{T}_m} = \min(o_i, o_j, o_k)\)로 설정된다. 삼각형 내부의 한 지점의 색상은 vertex 색상과 barycentric coordinate을 interpolation하여 얻는다. 따라서 미분 과정에서 vertex의 위치, 색상, 불투명도는 연결된 모든 삼각형으로부터 누적된 gradient를 받는다.

3. From soups to meshes

최적화 과정은 구조화되지 않은 표현을 구조화된 표현으로 점진적으로 변환하는 두 단계로 진행된다. 이러한 디자인은 학습 초기 단계에서 구조화되지 않은 표현이 제약 조건이 적어 최적화하기 더 쉽다는 점을 활용한다.

Stage 1. Triangle soup optimization

먼저, SfM을 통해 얻은 포즈를 아는 이미지 세트, 카메라 파라미터, sparse한 포인트 클라우드를 입력으로 사용한다. 각 3D 포인트에 대해, 해당 포인트를 중심으로 하는 정삼각형을 초기화한다. 이 삼각형의 크기는 가장 가까운 세 이웃 포인트까지의 평균 거리에 비례하며, orientation은 무작위로 설정된다. 모든 삼각형은 초기에는 반투명하게 정의된다 ($o_i = 0.28$).

Connectivity나 매니폴드 제약 조건 없이, 즉 구조화되지 않은 삼각형들의 집합체에서 최적화를 시작한다. 각 삼각형은 독립적으로 최적화되며 이미지 공간의 gradient에 따라 자유롭게 움직일 수 있다. 이러한 제약 없는 방식은 보이는 장면을 빠르게 커버하고 로컬 geometry와 외형에 신속하게 적응할 수 있도록 한다.

Stage 2. Mesh creation & refinement

Triangle soup을 연결된 메쉬로 변환하기 위해, 제한된 Delaunay triangulation을 수행한다. 이 연산은 먼저 표준 Delaunay tetrahedralization을 계산한 다음, dual 관계에 있는 Voronoi diagram의 edge들이 triangle soup의 표면과 교차하는 사면체 면들을 식별한다. 제한된 Delaunay triangulation은 표면을 근사화하는 메쉬를 생성하는 동시에, Delaunay 성질들을 해당 영역에 로컬하게 유지한다. 다른 방법들과 달리, 제한된 Delaunay triangulation은 새로운 vertex를 추가하거나 위치를 변경하지 않는다. 대신, 최적화된 vertex를 직접 재사용하여 공간 정확도와 학습된 외형을 모두 보존한다.

제한된 Delaunay triangulation을 통해 얻은 메쉬 connectivity를 바탕으로, vertex의 위치와 모양을 fine-tuning하기 위한 최적화를 진행한다. 인접한 삼각형들이 vertex를 공유하므로, 인접한 면의 gradient가 공유 vertex에 누적되어 각 vertex가 모든 인접 삼각형에 따라 일관되게 업데이트된다. Stage 1에서 이미 모든 공간 영역을 정확하게 포착할 수 있을 만큼 충분히 dense한 삼각형 집합이 이미 생성되었기 때문에 추가적인 면이나 vertex를 도입할 필요가 없다. 이러한 fine-tuning 단계를 거치면 기존 렌더링 엔진에서 높은 품질로 장면을 렌더링할 수 있는 완전히 불투명한 메쉬를 얻게 된다. 마지막 학습 iteration에서는 슈퍼샘플링을 활성화하여 작은 삼각형까지도 gradient를 받아 적절하게 최적화할 수 있도록 한다.

4. Optimizing meshes with opaque triangles

불투명한 삼각형으로만 구성된 메쉬를 최적화하는 것은 기존의 NeRF/3DGS 최적화와 비교하여 새로운 과제를 제시한다. 가려진 부분을 통해 gradient 전파가 가능하도록 하고 표현을 효과적으로 최적화하기 위해서는 학습 초기 단계에서 표현이 반투명 상태를 유지해야 한다. 이를 위해 제어할 수 있는 자유도는 두 가지가 있는데, 하나는 vertex별 불투명도 파라미터 $o$와 smoothness 파라미터 $\sigma$이다.

Opacity parameter scheduling

초기 5,000 iteration 동안에는 불투명도를 자유롭게 최적화한다. 그 후에는 삼각형을 더 불투명하게 만들도록 유도하기 위해 불투명도 값을 다음과 같이 parameterize한다.

\[\begin{equation} o^\prime (o) = O_t + (1 - O_t) \cdot \textrm{sigmoid} (o) \end{equation}\]

참고로, $O_t = 0$이면 sigmoid 함수가 불투명도를 0과 1 사이에서 부드럽게 조절한다. 반대로 $O_t = 1$이면 모든 불투명도가 1로 설정된다. 최적화 과정에서 $O_t$ 값을 0에서 1까지 선형적으로 증가시키면 이러한 동작을 부드럽게 제어할 수 있다.

Window parameter scheduling

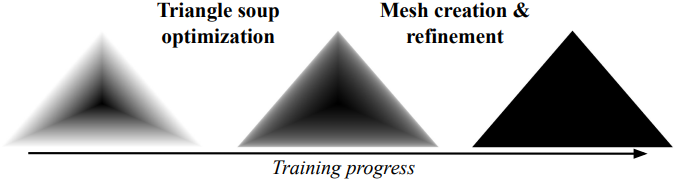
Window 파라미터 $\sigma$는 1.0으로 초기화되는데, 이는 삼각형의 중심에서 경계까지의 선형적인 변화에 해당하며, 모든 삼각형에서 공유되는 하나의 파라미터로 취급한다. Triangle soup에서 메쉬로 전환하는 학습 단계 전반에 걸쳐 $\sigma$는 1.0에서 0.0001까지 선형적으로 어닐링되어 초기 단계에서는 강력한 gradient flow를 보장하고 최적화 과정이 끝날 무렵에는 불투명한 삼각형으로 수렴한다.

5. Optimization details

Densification

초기 삼각형 집합이 충분히 dense하지 않을 수 있으므로, 3DGS-MCMC의 아이디어를 적용하여 추가적인 삼각형을 생성한다. 각 densification 단계에서, 후보 삼각형은 베르누이 샘플링을 사용하여 삼각형의 불투명도 $o$로부터 직접 구성된 확률 분포에서 샘플링하여 선택된다. Triangle Splatting과 마찬가지로 새로운 삼각형은 중점 분할을 통해 생성된다. 선택된 삼각형의 세 변의 중점을 연결하여 네 개의 작은 삼각형으로 분할한다. 새로운 중점들은 vertex 집합 $\mathcal{V}$에 추가되고, 인접한 두 vertex의 평균 색상과 불투명도가 할당된다.

초기 단계에서 connectivity를 활용함으로써 새로 생성되는 vertex의 수를 크게 줄일 수 있다. 연결된 상태에서 분할하면 분할 후 6개의 새로운 vertex만 생성되는 반면, 삼각형 집합이 있는 초기 설정에서는 12개의 새로운 vertex가 생성된다.

Pruning

5000 iteration (Stage 1, 불투명도 스케줄링 시작 직전)에서 불투명도 $o$가 0.2보다 작은 모든 삼각형을 제거하여 약 70%를 제거한다. 1단계의 나머지 과정에서는 모든 뷰에서 최대 볼륨 렌더링 블렌딩 가중치 $w = T \cdot o$를 모니터링하고 $w < O_t$일 때마다 pruning를 수행하여 표현이 더 불투명해짐에 따라 가려진 삼각형을 제거한다. Stage 2에서는 pruning이 비활성화되지만, 학습이 끝날 때 모든 학습 뷰에 대해 최종 pruning을 수행하여 렌더링되지 않은 삼각형을 제거한다.

Training losses

모든 vertex의 3D 위치 \(\textbf{v}_i\) vi, 불투명도 $o_i$, 그리고 spherical harmonics 색상 계수 \(\textbf{c}_i\)를 최적화한다. 학습 loss는 3DGS의 photometric loss \(\mathcal{L}_\textrm{3DGS}\), 3DGS-MCMC의 opacity loss \(\mathcal{L}_o\), 뒤에서 설명할 depth alignment loss \(\mathcal{L}_z\), 2DGS의 normal loss \(\mathcal{L}_n\), Hierarchical 3DGS의 depth loss \(\mathcal{L}_d\)를 결합한다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{3DGS} + \beta_o \mathcal{L}_o + \beta_z \mathcal{L}_z + \beta_n \mathcal{L}_n + \beta_d \mathcal{L}_d \end{equation}\]

Depth alignment loss

매니폴드 생성을 촉진하기 위해 vertex-to-surface depth loss를 사용하여 삼각형을 관찰된 depth map에 정렬한다. 이를 위해 각 3D 좌표가 $(x_i, y_i, z_i)$인 vertex \(\textbf{v}_i\)에 대하여, 렌더링된 depth map에서 $(x_i, y_i)$의 예측 깊이 \(z_i^\ast\)를 샘플링하고 $z_i$와의 깊이 차이에 페널티를 부여한다.

\[\begin{equation} \mathcal{L}_z = \frac{1}{N} \sum_{i=1}^N \vert z_i - z_i^\ast \vert \end{equation}\]

이 공식은 각 vertex에 독립적으로 작용한다.

Rendering equation

각 이미지 픽셀 $\textbf{p}$의 최종 색상은 깊이 순서대로 겹치는 모든 삼각형의 기여도를 누적하여 계산된다.

\[\begin{equation} C(\textbf{p}) = \sum_{n=1}^N \textbf{c}_{T_n} o_{T_n} I (\textbf{p}) \left( \prod_{i=1}^{n-1} (1 - o_{T_i} I (\textbf{p})) \right) \end{equation}\]

학습이 끝나면 이는 \(C(\textbf{p}) = c_{T_n} I(\textbf{p})\)로 단순화되므로 픽셀당 한 번의 평가만 필요하게 되어 렌더링 프로세스가 크게 가속화된다.

Experiments

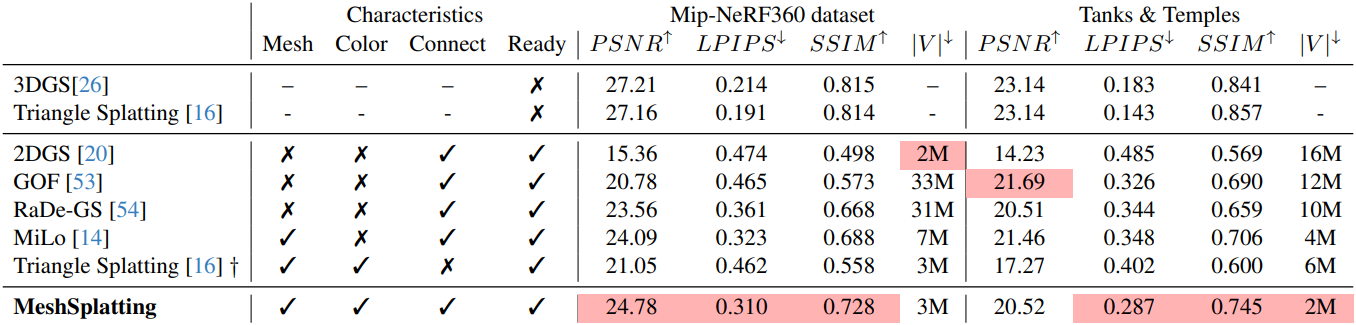
1. Mesh-based NVS

다음은 메쉬 기반 novel view synthesis를 비교한 결과이다.

2. Training speed & memory

다음은 학습 속도 및 메모리 사용량을 MipNeRF-360에서 비교한 결과이다.

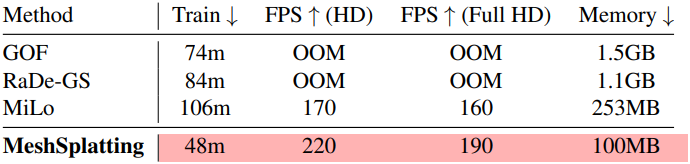
3. Applications

다음은 SAM 2로 얻은 segmentation mask로 object segmentation을 수행한 예시이다.

4. Analysis

다음은 인접한 삼각형과의 connectivity에 따른 삼각형의 분포이다.

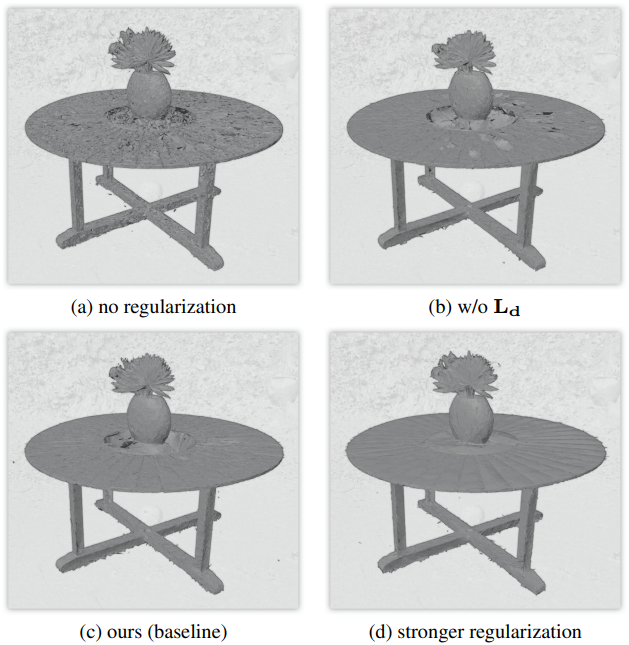
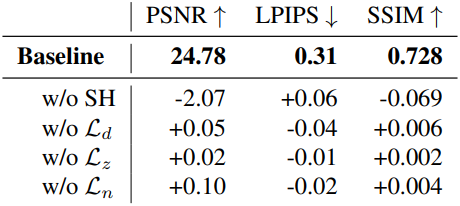
다음은 ablation 결과이다. (Mip-NeRF360)