[논문리뷰] Mesh Silksong: Auto-Regressive Mesh Generation as Weaving Silk

arXiv 2025. [Paper] [Page] [Github]
Gaochao Song, Zibo Zhao, Haohan Weng, Jingbo Zeng, Rongfei Jia, Shenghua Gao
University of Hong Kong | Tencent Hunyuan 3D | Math Magic
3 Jul 2025

Introduction

Autoregressive한 메쉬 생성의 핵심은 autoregressive 모델의 강력한 생성 능력을 최대한 활용하는 효과적인 토큰 표현을 설계하는 것이다. Autoregressive 모델의 본질적인 불안정성을 고려할 때, 핵심 과제는 manifold topology, watertightness, 표면 normal 일관성과 같은 위상 구조를 유지하면서 메쉬의 정보를 효과적으로 압축하는 것이다.

현재 효율적인 mesh-to-token 변환 알고리즘은 크게 트리 순회 기반(ex. EdgeRunner, TreeMeshGPT)과 로컬 패치 기반(ex. BPT, Nautilus, DeepMesh)의 두 가지 카테고리로 나눌 수 있다. 트리 순회 방식은 half-edge 데이터 구조를 활용하여 manifold topology를 보존하지만, 삼각형 순회 중 오차가 누적되어 메쉬 생성이 불안정해지는 문제가 있다. 반면, 로컬 패치 방식은 로컬 삼각형 패치를 독립적으로 처리하여 더 안정적인 메쉬를 생성하지만, 이러한 메쉬는 종종 non-manifold이기 때문에 UV unwrapping, 3D 프린팅, 물리 시뮬레이션 등에 응용하는 데에는 적합하지 않다.

또한, 두 카테고리의 접근 방식은 모두 다음과 같은 한계에 직면한다.

1. 중복되는 vertex 압축
2. 글로벌한 구조 인식 부족

이러한 문제를 해결하기 위해, 본 논문에서는 새로운 메쉬 tokenization 알고리즘을 제안하였다. 주어진 시작 vertex까지의 그래프 거리를 기준으로 vertex를 여러 layer로 분류하고, layer별로 정렬한 후, layering되고 정렬된 vertex들을 기반으로 인접 행렬을 계산하여 topology를 인코딩한다. 그런 다음, 인접 행렬에서 압축된 vertex 토큰과 topology 토큰을 메쉬 표현을 위한 통합된 형식으로 정리한다. 기존 방식과 비교하여, 이 방법은 각 vertex를 한 번만 압축하여 중복 vertex 정보를 약 50% 줄인다.

본 논문에서 제안하는 방법을 BPT에서 제안하는 block-wise indexing (vertex당 토큰 3개에서 2개로 줄임)과 결합하면 최종 압축률이 0.26에서 0.22로 향상되어 메쉬 압축 효율을 높이고 동일한 토큰 길이 내에서 더욱 미세한 기하학적 디테일 묘사를 가능해진다. 또한, 메쉬의 연결 요소(connected component)에 대해 개별적으로 연산하고 특수 토큰을 사용하여 표시하기 때문에 메쉬의 연결 요소에 민감하다. 이를 통해 생성 모델은 전반적인 기하학적 위상에 집중하고, 간과되기 쉬운 작은 연결 요소들을 효과적으로 포착할 수 있다. Manifold 기반 메쉬 표현 방식인 본 논문의 접근법은 watertightness를 강력하게 지원하고 표면 normal 일관성에 대한 강력한 제약 조건을 적용하여 뛰어난 기하학적 특성을 보여준다.

Method

1. Non-manifold Edges Processing

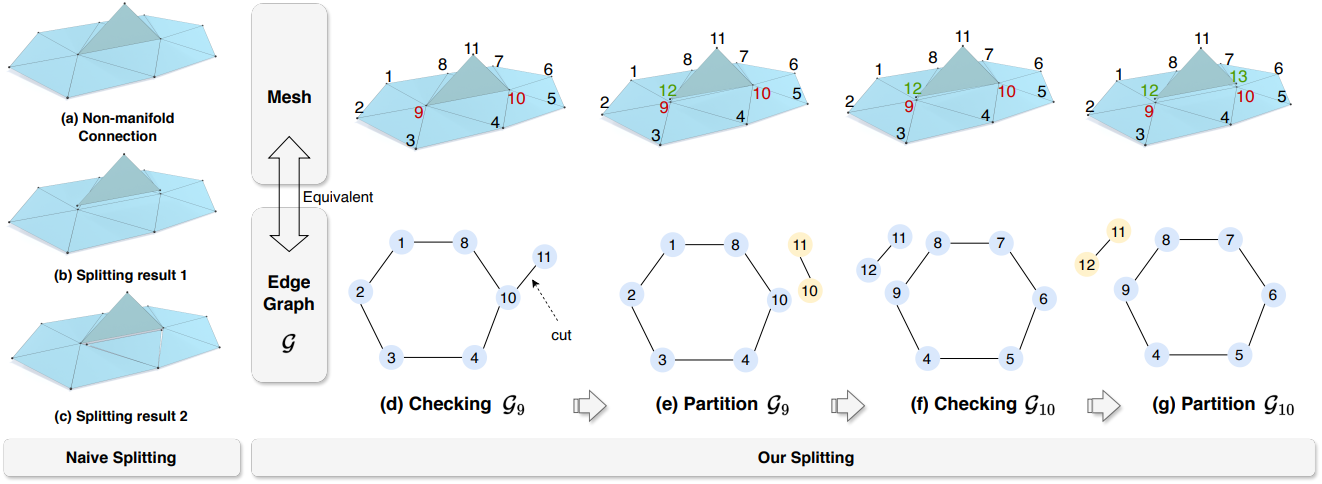
메쉬의 non-manifold edge 3개 이상의 면이 공유하는 edge를 말한다 (위 그림에서 edge 9-10). EdgeRunner에서 한 것처럼 이를 제거하는 단순한 방법은 모든 삼각형 edge를 다시 탐색하고 세 번째로 발생하는 edge를 bounding edge로 표시하는 것이다. 그러나 이렇게 하면 삼각형이 나타나는 순서에 따라 여러 가지 결과가 발생할 수 있다. 예를 들어, (b)와 (c)에 나와 있듯이 두 결과 모두 non-manifold edge가 제거되었지만 (c)는 메쉬 표면의 완전성을 파괴하여 다음 단계들에 적합하지 않다.

이를 해결하기 위해 이 문제를 동등한 edge graph 분할 문제로 변환한다. Vertex $i$의 edge graph \(\mathcal{G}_i\)는 vertex를 포함한 모든 면으로 형성된 무향 그래프(undirected graph)를 나타낸다. (d)에 나와 있듯이, edge graph \(\mathcal{G}_9\)의 “node”는 메쉬에서 기준 vertex 9에 연결된 edge를 나타내고, edge graph의 “edge”는 “node”와 기준 vertex 9에 의해 형성된 메쉬의 면을 나타낸다. 메쉬의 manifold 구조를 보장하기 위해 각 메쉬 vertex의 edge graph는 분기가 없는 사이클 또는 체인 형태여야 하며, 연결 요소가 하나만 있어야 한다.

전체 알고리즘은 위 그림의 (d)-(g)에 설명되어 있다. \(\mathcal{G}_9\)를 확인한 후, 분기된 “edge” 10-11(메쉬의 면 9-10-11)을 쉽게 감지하여 사이클에서 분리한다. 그런 다음 (e)에서 분리된 연결 요소 10-11을 edge graph에서 제외한다. 이는 메쉬의 vertex 9에서 면 9-10-11을 분리하고 메쉬 edge 10-11에 새로운 vertex 12를 등록하는 것과 같다. (e) 이후에는 \(\mathcal{G}_{10}\)의 edge graph도 업데이트된다. 그런 다음 (f)와 같이 \(\mathcal{G}_{10}\)을 확인하는 작업을 시작한다. 알고리즘은 BFS 순회를 통해 모든 non-manifold point를 따라 진행하며, 각 vertex의 edge graph를 동적으로 업데이트한다.

2. Vertexes Layering and Sorting

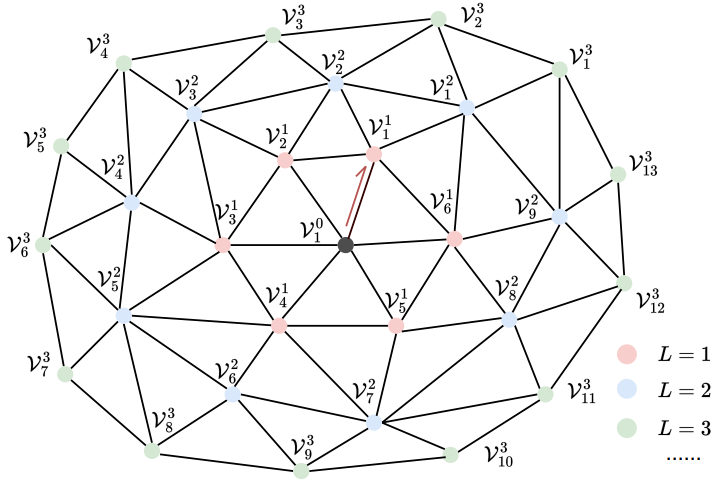
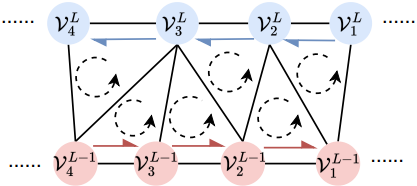
Manifold 메쉬 $\mathcal{M}$과 시작 half-edge가 주어지면 모든 vertex $\mathcal{V}$에 고유한 좌표 $(L, i)$를 할당할 수 있으며, vertex를 \(\mathcal{V}_i^L\)로 표시한다. 시작 half-edge의 두 vertex는 \(\mathcal{V}_1^0\)과 \(\mathcal{V}_1^1\)로 표시한다. Layer 번호 $L$은 $\mathcal{M}$의 edge만으로 초기 vertex \(\mathcal{V}_1^0\)에 대한 최단 경로를 나타내며 BFS 탐색으로 쉽게 얻을 수 있다. Layer order $i$는 같은 layer $L$에 있는 vertex의 순서를 나타내며 layer $L − 1$에 있는 vertex의 로컬한 순서를 기반으로 얻을 수 있다.

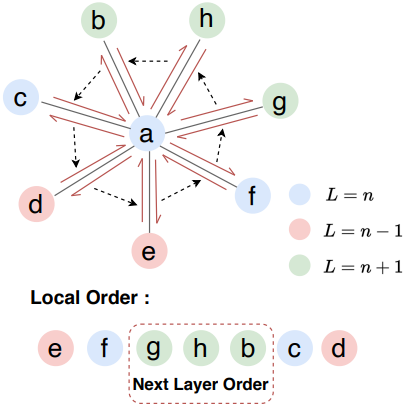
위 그림을 예로 들면, layer $L$의 vertex a에 대해 이웃 vertex는 먼저 half-edge 데이터 구조에 따라 시계 반대 방향으로 배열할 수 있으므로 layer $L + 1$에 대한 3개 vertex의 순서 (g, h, b)가 결정된다. 또한, layer $L$의 모든 정렬된 vertex가 주어지면, $L + 1$ 층의 모든 vertex의 순서는 다음과 같은 방식으로 결정될 수 있다. 메쉬의 시작 half-edge \(\mathcal{V}_1^0\)과 \(\mathcal{V}_1^1\)이 주어지면, 각 layer의 정렬된 vertex의 순서는 차례대로 결정될 수 있다. 실제로는 주어진 메쉬의 모든 half-edge를 y-z-x 순서로 정렬하고 가장 작은 half-edge를 시작 half-edge로 선택한다.

3. Layer Adjacency Matrices Compression

Vertex layering 및 정렬 후, 메쉬 vertex의 연결은 self-layer 연결 또는 between-layer 연결의 두 가지 상황으로 분류된다. Self-layer 연결은 연결된 두 vertex가 같은 layer $L$에 속하는 것을 의미하고, between-layer 연결은 연결된 두 vertex가 서로 다른 layer $L$과 $(L−1)$에 속하는 것을 의미한다. 따라서, layer $L$의 vertex가 주어졌을 때, Self-Layer Matrix \(\mathcal{S}_L\)과 Between-Layer Matrix \(\mathcal{B}_L\)이라는 두 인접 행렬을 통해 관련 위상 연결을 설명한다.

Self-Layer Matrix 압축

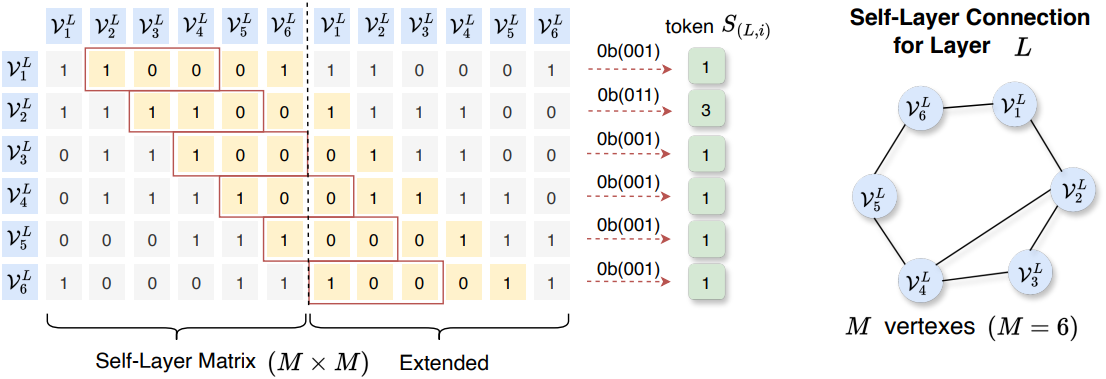
Self-Layer Matrix \(\mathcal{S}_L\)은 $M \times M$의 0-1 대칭 행렬이며, 여기서 $M$은 layer $L$의 vertex 번호를 나타낸다. 목표는 행렬의 $M$개 행을 $M$개의 토큰으로 압축하는 것이다. 여기서 행 $i$의 토큰 인덱스는 $S_{(L,i)}$로 나타낸다. \(\mathcal{S}_L\)을 압축하는 쉬운 방법은 모든 행에 binary coding을 직접 적용하는 것이다. 그러나 토큰의 word table은 $2m$개가 되며, 여기서 $m$은 모든 layer의 최대 vertex 수이다. 이렇게 큰 word table은 허용되지 않지만, 행렬의 sparsity는 효율적인 압축을 위한 단서를 제공한다.

1. 대칭 행렬을 $M \times 2M$으로 확장한다. 이때 행렬의 $(i, i)$는 쓸모가 없으며, 각 행의 유효한 값 번호는 위 그림의 노란색으로 표시된 $M − 1$개씩이다.
2. 크기가 $W$인 window를 행 $(i, i + 1)$에서 $(i, i + 1 + W)$까지 배치하여 binary coding을 계산한다 (그림에서 $W=3$인 빨간색 상자). 이는 self-layer 연결이 인접한 vertex에서 발생하는 경향이 있기 때문이다.

실제로 $W$는 8로 설정되고, window는 일반적으로 window 외부에 “1”이 나타나지 않으므로 슬라이드되지 않는다. 위 그림에서 (1, 6)과 같은 위치의 window 외부에 있는 “1”은 실제로 (6, 7)의 “1”로 반복되며, 실제로는 제거된다. Self-Layer Matrix의 초기 word table 크기는 $2^W$이다. “1”이 window 외부에 나타나는 특수한 상황에서는 word table 크기를 $2^W + m$으로 확장하여 처리한다.

Between-Layer Matrix 압축

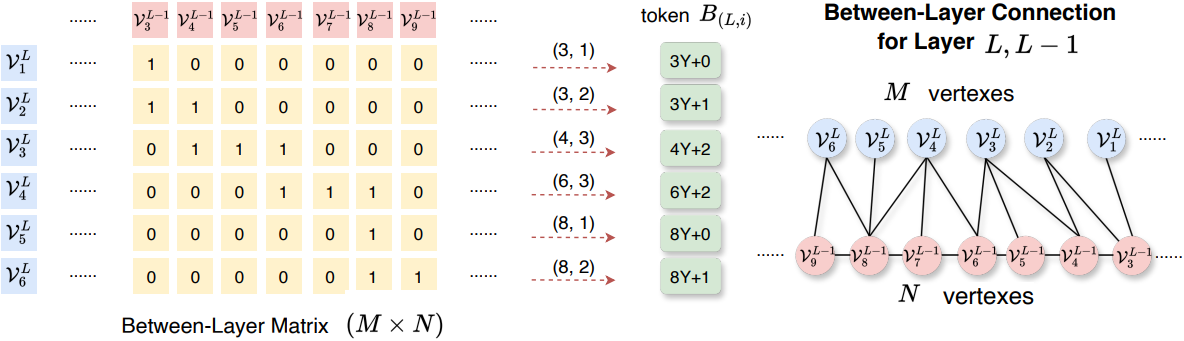
Between-Layer Matrix \(\mathcal{B}_L\)은 크기가 $M \times N$인 0-1 행렬이다. 여기서 $M$은 layer $L$의 vertex 개수이고, $N$은 layer $L-1$의 vertex 개수이다. 연결 규칙이 Self-Layer Matrix와 다르다는 점을 고려하여 다른 압축 방식을 적용한다. “1”은 각 행에 연속적으로 나타나는 경향이 있다. 예를 들어, 행 3의 경우 (3, 4), (3, 5), (3, 6)에 연속된 세 개의 “1”이 있으므로 먼저 행 3을 $(x, y) = (4, 3)$으로 표시한다. 여기서 $x \in [1, m]$은 “1”의 시작 열 인덱스를 나타내고, $y \in [1, Y]$는 연속된 “1”의 개수를 나타내며, $Y$는 미리 정의된 최대로 연속되는 “1”의 개수이다. 그러면 $B_{(L,i)}$의 토큰 인덱스는 $x \cdot Y + y − 1$이어야 한다. 위 그림에 표시된 단순화된 상황에서 Between-Layer Matrix의 word table 크기는 $m \cdot Y$이다.

실제로 “1”은 두 번 이상 연속해서 나타나므로, $Y$는 다음과 같다.

\[\begin{equation} Y = 2 \cdot W^\prime + 2 \cdot \binom{W^\prime - 1}{2} + \binom{W^\prime - 1}{3} \end{equation}\]

($W^\prime$은 Between-Layer Matrix에 대하여 미리 정의된 window 크기)

4. Token Packing and Model

Token Packing

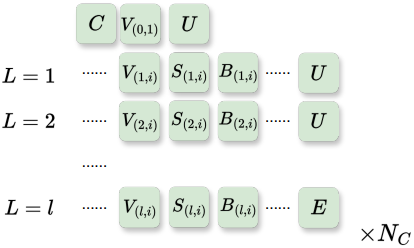
Layer $L$의 $M$개 vertex에 대해 세 가지 유형의 토큰, 즉 vertex 토큰 $V_{(L,i)}$와 topology 토큰 $S_{(L,i)}$, $B_{(L,i)}$가 있다. Vertex 토큰 $V_{(L,i)}$는 vertex의 위치를 ​​압축하고 일반적으로 quantize된 x-y-z 좌표를 나타내는 3개의 sub-token을 포함한다. BPT의 block-wise indexing을 사용하면 sub-token 수를 2개로 줄어든다. 두 개의 topology 토큰 $S_{(L,i)}$와 $B_{(L,i)}$는 일반적으로 서로 하나의 sub-token을 포함한다.

학습을 위한 전체 시퀀스를 얻으려면 메쉬의 연결 요소를 나타내는 토큰 C에서 시작한다. 메쉬에 $N_C$개의 연결 요소가 있는 경우 $N_C$개의 C 토큰이 있고 앞서 설명한 알고리즘들은 각 연결 요소에 대해 총 $N_C$번 수행된다. Vertex \(\mathcal{V}_i^L\)에 대해 $V_{(L,i)}$, $S_{(L,i)}$, $B_{(L,i)}$를 함께 묶고, 각 vertex의 토큰을 layer order에 따라 배열한다. \(\mathcal{V}_1^0\)에 대한 vertex 토큰은 맨 처음에 배치되며, topology 토큰은 없다. 각 layer의 토큰은 “up-layer” 제어 토큰 U로 구분되고, 마지막 토큰은 연결 요소의 끝을 나타내는 다른 제어 토큰 E로 대체된다.

모델 아키텍처

학습에 사용하는 핵심 모델은 decoder-only transformer이며, 각 layer는 cross-attention layer, self-attention layer, feed-forward network로 구성된다. 포인트 클라우드를 조건으로 한 메쉬 생성을 위해, 포인트 클라우드 feature는 Michelangelo 모델에서 추출되어 cross-attention을 통해 autoregressive 모델에 주입된다. Michelangelo 모델과 decoder-only transformer는 공동으로 학습된다.

학습 전략

학습 데이터의 long-tailed 분포를 처리하고 긴 시퀀스 토큰의 학습을 촉진하기 위해 progressively-balanced sampling을 사용한다. 이 전략은 학습 과정에서 인스턴스 균형 샘플링과 클래스 균형 샘플링을 interpolation한다. 100개의 면들을 기준으로 분류하는 클래스 $j$에 대해, epoch $t$에서 샘플링 확률 \(p_j^\textrm{PB} (t)\)는 다음과 같다.

\[\begin{equation} p_j^\textrm{PB} (t) = (1 - t/T) p_j^\textrm{IB} + (t/T) p_j^\textrm{CB} \end{equation}\]

($p_j^\textrm{IB}$와 $p_j^\textrm{CB}$는 인스턴스 균형 샘플링과 클래스 균형 샘플링의 확률, $t$는 현재 epoch이며, $T$는 총 epoch 수)

초기 epoch은 인스턴스 균형 샘플링에 중점을 두는 반면, 나중 epoch은 클래스 균형 샘플링을 우선시하여 긴 토큰 시퀀스를 가진 long-tailed 클래스를 효과적으로 학습할 수 있다.

Loss Function

Autoregressive 모델을 학습하기 위해, 예측된 토큰 logit과 실제 토큰 시퀀스 간의 차이를 최소화하는 표준 cross-entropy loss를 사용한다.

\[\begin{equation} \mathcal{L}_\textrm{ce} = - \sum_{t=1}^{T-1} S_{t+1} \log \hat{S}_t \end{equation}\]

(\(\hat{S}_t\)는 예측된 토큰 logit, $S_{t+1}$은 one-hot GT 토큰)

Experiments

• 데이터셋: gObjaverse, ShapeNetV2, 3D-FUTURE, Toys4K
• 구현 디테일
  • transformer
    • 레이어 수: 24
    • hidden size: 1,024
    • 파라미터 수: 500M
  • GPU: H800 16개로 15일 학습
  • optimizer: AdamW (\(\beta_1 = 0.9\), \(\beta_2 = 0.99\))
  • learning rate: $1 \times 10^{-4}$에서 $5 \times 10^{-5}$로 코사인으로 감소

1. Comparation Results

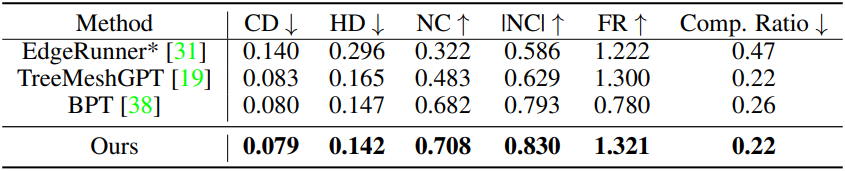
다음은 다른 메쉬 생성 방법들과 비교한 결과이다.

2. Ablation Study

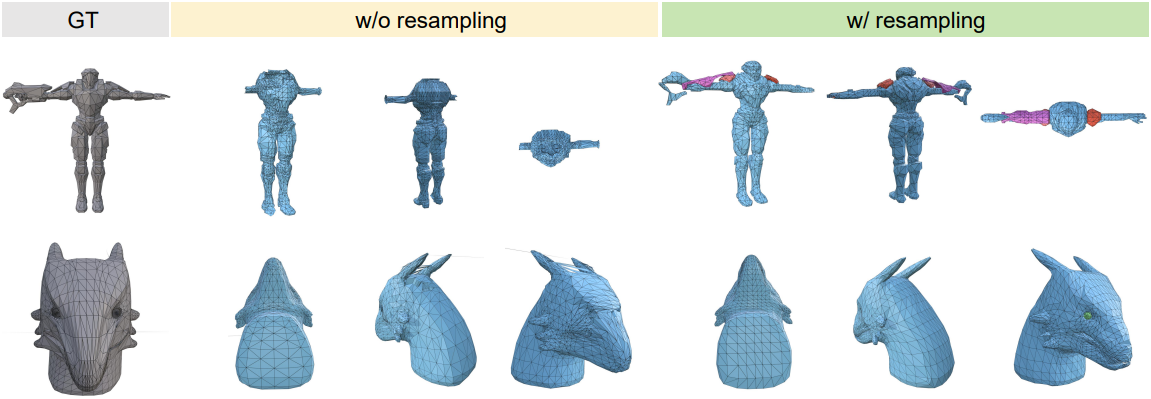
다음은 ablation study 결과이다.

3. Geometric Properties

본 논문의 메쉬 표현 방식은 normal 일관성을 강하게 만족한다. 아래 예시와 같이 디코딩된 삼각형들은 모두 같은 방향의 normal을 가진다.

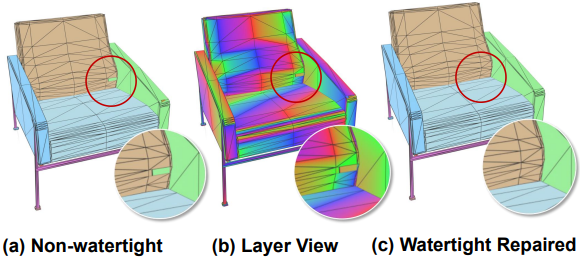
Topology 토큰 예측 오차가 가끔 발생하여 빈틈이 없을 것으로 예상되는 메쉬 표면에 구멍이 생길 수 있다. 본 논문의 메쉬 표현 방식은 본질적으로 watertight 감지 및 복구를 어느 정도 지원한다. 아래 예시는 각 layer의 vertex를 등고선으로 시각화한 것이다. 표면 구멍은 Self-Layer Matrix 또는 Between-Layer Matrix의 특정 entryrk 1이 아닌 0으로 잘못 예측되어 발생하며, 쉽게 감지 및 복구할 수 있다.

Limitation

1. Vertex 토큰 외에도, topology 토큰이 존재하여 최종 vocabulary 크기가 최대 10,267로 제한된다.
2. Layer당 최대 vertex 수에 해당하는 $m$을 미리 정의해야 한다.