Diffusion은 신이고 GPT는 무적이다

CVPR 2024 (Highlight). [Paper] [Page] [Github]
Yawar Siddiqui, Antonio Alliegro, Alexey Artemov, Tatiana Tommasi, Daniele Sirigatti, Vladislav Rosov, Angela Dai, Matthias Nießner
Technical University of Munich | Politecnico di Torino | AUDI AG
27 Nov 2023

Introduction

최근 3D 비전 연구에서는 복셀, 포인트 클라우드, 신경망과 같은 표현을 사용하는 생성적 3D 모델에 큰 관심을 보이고 있다. 그러나 이러한 표현은 후속 애플리케이션에서 사용하기 위해 후처리 과정을 거쳐 메쉬로 변환해야 한다. 하지만 이 과정에서는 등위면(iso-surface) 처리 과정에서 과도하게 매끄럽고 울퉁불퉁한 아티팩트가 나타나는 과도하게 테셀레이션된 메쉬가 생성된다. 반면, 실제 사람이 모델링한 3D 메쉬는 훨씬 적은 삼각형으로 선명한 디테일을 유지하면서도 컴팩트한 표현을 제공한다.


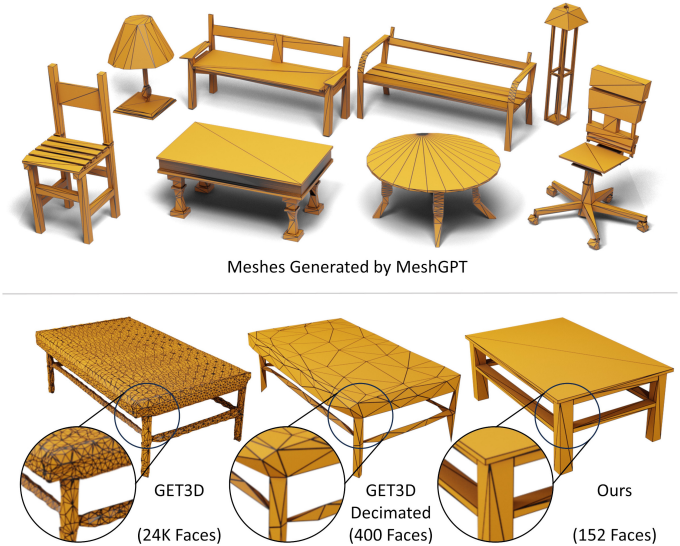
따라서 본 논문에서는 메쉬 표현을 삼각형 집합으로 직접 생성하는 MeshGPT를 제안하였다. LLM의 발전에서 영감을 받아, 직접적인 시퀀스 생성 방식을 채택하여 삼각형 메쉬를 삼각형 시퀀스로 합성한다. 텍스트 생성 패러다임에 따라 먼저 삼각형의 vocabulary를 학습시킨다. 삼각형은 인코더를 통해 quantize된 latent 임베딩으로 인코딩된다. 학습된 삼각형 임베딩이 로컬한 기하학적 및 위상적 feature를 유지하도록 하기 위해 graph convolutional encoder를 사용한다. 이러한 삼각형 임베딩은 ResNet 디코더에 의해 디코딩되는데, ResNet 디코더는 삼각형을 나타내는 토큰 시퀀스를 처리하여 꼭짓점 좌표를 생성한다. 이렇게 학습된 vocabulary를 기반으로 GPT 기반 아키텍처를 학습시켜 메쉬를 나타내는 삼각형 시퀀스를 autoregressive하게 생성할 수 있다.

Method

1. Learning Quantized Triangle Embeddings

Transformer는 이전에 생성된 토큰을 기반으로 새로운 토큰 시퀀스를 합성한다. Transformer를 사용하여 메쉬를 생성하려면 토큰과 함께 생성 순서 규칙을 정의해야 한다.

시퀀스 순서의 경우, 면들을 가장 낮은 vertex 인덱스를 기준으로 정렬하고, 그 다음으로 낮은 vertex 인덱스를 기준으로 정렬하는 방식을 사용한다. Vertex들은 z-y-x 순서(z는 세로축)로 정렬되며, 가장 낮은 vertex부터 가장 높은 vertex까지 순차적으로 정렬된다. 각 면 내에서 인덱스는 순환적으로 순열되어 가장 낮은 인덱스가 맨 앞에 오도록 한다.

생성할 토큰을 정의하기 위해 메쉬 $\mathcal{M}$을 삼각형 시퀀스로 표현한다.

\[\begin{equation} \mathcal{M} := (f_1, f_2, \ldots, f_N), \quad f_i \in \mathbb{R}^{n_\textrm{in}} \end{equation}\]

($N$은 삼각형 면의 수)

각 삼각형을 표현하는 간단한 방법은 세 개의 꼭짓점을 사용하여 총 9개의 좌표를 구성하는 것이다. Discretization을 통해 이러한 좌표는 토큰으로 취급될 수 있다. 이 경우 시퀀스 길이는 $9N$이 된다. 그러나 좌표를 토큰으로 직접 사용할 때 두 가지 주요 문제가 발생한다.

  1. 각 면이 9개의 값으로 표현되기 때문에 시퀀스 길이가 지나치게 길어진다. 이 길이는 제한된 context window를 갖는 transformer 아키텍처에서는 잘 확장되지 않는다.
  2. 삼각형의 discrete한 위치를 토큰으로 표현하는 것은 기하학적 패턴을 효과적으로 포착하지 못한다. 이는 이러한 표현 방식이 이웃 삼각형에 대한 정보가 부족하고 메쉬 분포의 prior를 포함하지 않기 때문이다.


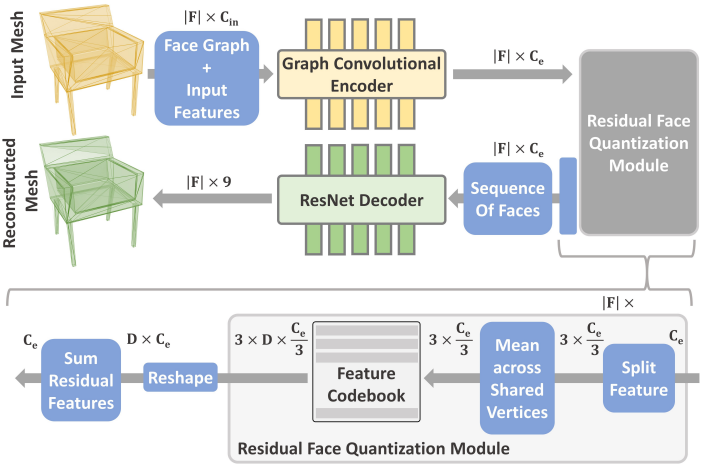
이를 해결하기 위해, bottleneck에 residual vector quantization (RQ)을 적용한 인코더-디코더 아키텍처를 활용하여 삼각형 메쉬 집합에서 기하학적 임베딩을 학습시킨다.

인코더 $E$는 메쉬 면에 graph convolution들을 적용하는데, 각 면은 node를 형성하고 이웃 면은 undirected edge로 연결된다. 입력 면에 대한 node feature은 vertex의 9개 위치 인코딩된 좌표, 면의 normal, edge 사이의 각도, 그리고 면적으로 구성된다. 이러한 feature들은 SAGEConv layer들의 스택을 통해 처리되어 각 면에 대한 feature 벡터가 추출된다. 이 접근 방식은 각 면에 대해 기하학적으로 풍부한 feature \(z_i \in \mathbb{R}^{n_z}\)를 추출하고, 학습된 임베딩에 이웃 정보를 융합한다.

\[\begin{equation} \textbf{Z} = (z_1, z_2, \ldots, z_N) = E (\mathcal{M}) \end{equation}\]

Quantization의 경우 residual vector quantization (RQ)을 사용한다. 면당 하나의 코드를 사용하는 것은 정확한 재구성에 충분하지 않다. 대신 면당 $D$개의 코드를 스택으로 사용한다. 또한 면당 $D$개의 코드를 직접 사용하는 대신, 먼저 feature 채널을 vertex 간에 나누고 공유 vertex 인덱스로 feature를 집계한 다음, 이러한 vertex 기반 feature를 quantize하여 vertex당 $\frac{D}{2}$개의 코드를 사용한다. 따라서 사실상 면당 $D$개의 코드가 된다. 이렇게 하면 transformer에서 더 쉽게 학습할 수 있는 시퀀스가 ​​생성된다.

구체적으로, codebook $\mathcal{C}$가 주어졌을 때, 깊이가 $D$인 RQ는 feature $\textbf{Z}$를 다음과 같이 나타낸다.

\[\begin{aligned} \textbf{T} &= (t_1, t_2, \ldots, t_N) = \textrm{RQ} (\textbf{Z}; \mathcal{C}, D) \\ t_i &= (t_i^1, t_i^2, \ldots, t_i^D) \end{aligned}\]

($t_i$는 토큰 스택이고, 각 토큰 $t_i^d$는 codebook $\mathcal{C}$의 임베딩 $\textbf{e} (t_i^d)$에 대한 인덱스)

그런 다음, 디코더는 quantize된 면 임베딩을 삼각형으로 디코딩한다. 먼저, $D$개의 feature 스택은 임베딩 간 합산과 vertex 간 concat을 통해 면당 하나의 feature가 된다.

\[\begin{aligned} \hat{\textbf{Z}} &= (\hat{z}_1, \ldots, \hat{z}_N) \\ \hat{z}_i &= \oplus_{v=0}^2 \sum_{d=1}^{D/3} \textbf{e} (t_i^{3d+v-2}) \end{aligned}\]

면 임베딩은 앞서 설명한 순서대로 배열되며, 1D ResNet34 디코딩 head $G$는 결과 시퀀스를 처리하여 각 면을 나타내는 9개의 좌표를 갖는 재구성된 메쉬 $\hat{\mathcal{M}} = G (\hat{\textbf{Z}})$를 출력한다. 이러한 좌표를 discrete한 값의 집합에 대한 확률 분포로 예측하는 것이 실수 값으로 직접 예측하는 것보다 더 정확한 재구성을 제공한다. Discrete한 메쉬 좌표에 대한 cross-entropy loss와 임베딩에 대한 commitment loss가 재구성 프로세스를 가이드한다.


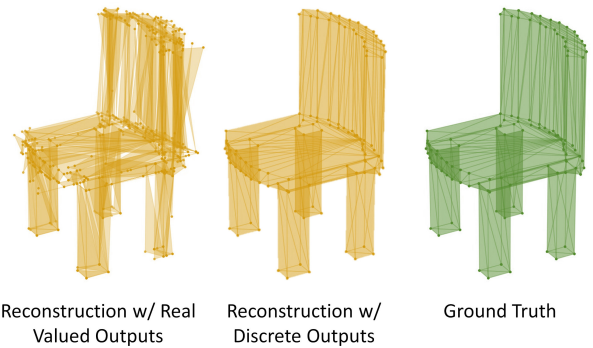
학습 후, 인코더 $E$와 codebook $\mathcal{C}$는 transformer 학습에 통합된다. $\vert \textbf{T} \vert = DN$이므로, 이 시퀀스는 $D < 9$일 때의 $9N$ 길이의 tokenization보다 더 간결하다.

2. Mesh Generation with Transformers


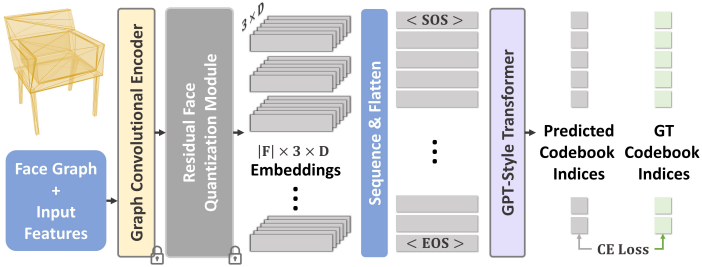
GPT 모델 계열의 decoder-only transformer 아키텍처를 사용하여 학습된 codebook의 인덱스 시퀀스로 메쉬를 예측한다. 이 transformer의 입력은 GraphConv 인코더 $E$를 사용하여 메쉬 $\mathcal{M}$에서 추출하고 RQ를 사용하여 quantize된 임베딩들로 구성된다. 임베딩에는 학습된 시작 및 종료 임베딩이 앞뒤로 추가된다. 또한, 시퀀스에서 각 면의 위치와 면 내 각 임베딩의 인덱스를 나타내는 학습된 discrete한 위치 인코딩이 추가된다. 그런 다음, feature들은 multi-head self-attention layer들의 스택을 통과하며, 여기서 transformer는 시퀀스에서 다음 임베딩의 codebook 인덱스를 예측하도록 학습된다.

\[\begin{equation} \prod_{i=1}^N \prod_{d=1}^D p (t_i^d \vert \textbf{e}(t_{< i}^d), \textbf{e}(t_i^{< d}); \theta) \end{equation}\]

Transformer가 학습되면 beam sampling을 사용하여 시작 토큰부터 종료 토큰에 도달할 때까지 토큰 시퀀스를 autoregressive하게 생성할 수 있다. 이 토큰 시퀀스로 인덱싱된 codebook 임베딩은 디코더 $G$에 의해 디코딩되어 메쉬를 생성한다. 이 출력은 처음에는 이웃 면에 대한 중복된 정점으로 구성된 ‘triangle soup’를 형성하므로, MeshLab을 사용하여 가까운 vertex를 병합하는 간단한 후처리 연산을 적용하여 최종 메쉬를 생성한다.

Experiments

  • 데이터셋: ShapeNetV2
  • 구현 디테일
    • RQ
      • 깊이: 2 (면당 $D = 6$개의 임베딩)
      • 임베딩 차원: 192
      • EMA로 동적으로 codebook 업데이트
      • 디코더는 128개의 클래스에 대하여 예측 (즉, 공간을 $128^3$로 discretization)
      • GPU: A100 2개로 약 2일 소요
    • Transformer
      • 모델: GPT2-medium
      • context window: 4,096
      • GPU: A100 4개로 약 5일 소요
    • optimizer: Adam
    • effective batch size: 64
    • learning rate: $1 \times 10^{-4}$

1. Results

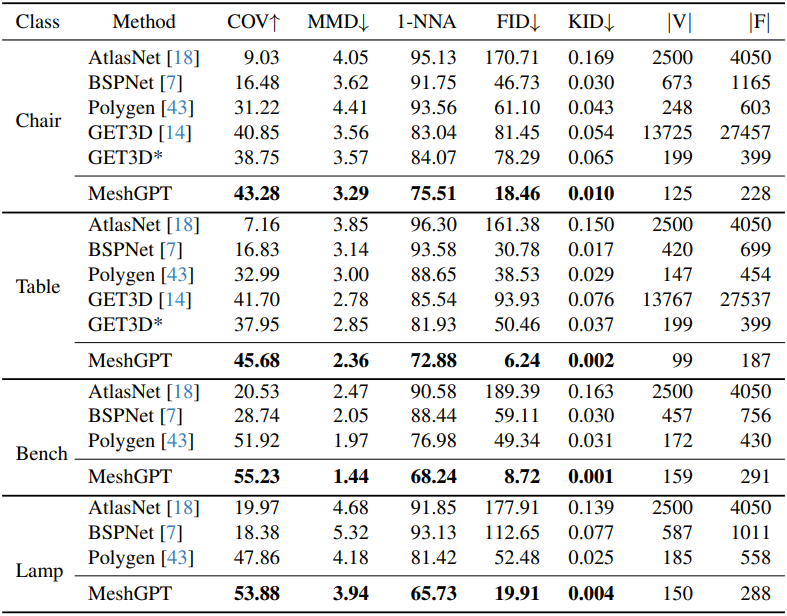
다음은 ShapeNet 데이터셋에 대한 메쉬 생성을 비교한 결과이다.


다음은 user study 결과이다.


다음은 ShapeNet 의자 카테고리에 대하여 생성된 샘플들과 가장 비슷한 학습 데이터를 비교한 결과이다.


다음은 부분적인 메쉬가 주어졌을 때 나머지를 완성한 예시들이다.

2. Ablations

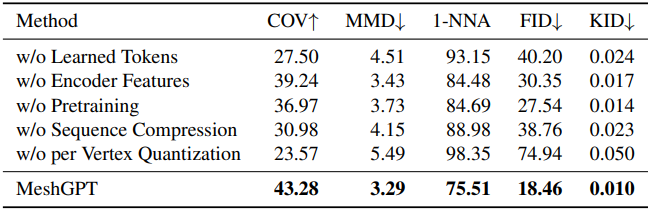
다음은 ablation 결과이다.

Limitations

  1. Autoregressive한 특성으로 인해 샘플링이 느리다. (30~90초)
  2. 단일 물체 생성에만 초점이 맞춰 있다.

You may also enjoy