[논문리뷰] Mesh-based Gaussian Splatting for Real-time Large-scale Deformation

arXiv 2024. [Paper]
Lin Gao, Jie Yang, Bo-Tao Zhang, Jia-Mu Sun, Yu-Jie Yuan, Hongbo Fu, Yu-Kun Lai
Beijing Key Laboratory of Mobile Computing and Pervasive Device | University of Chinese Academy of Sciences | Chinese Academy of Sciences | City University of Hong Kong | Cardiff University
7 Feb 2024

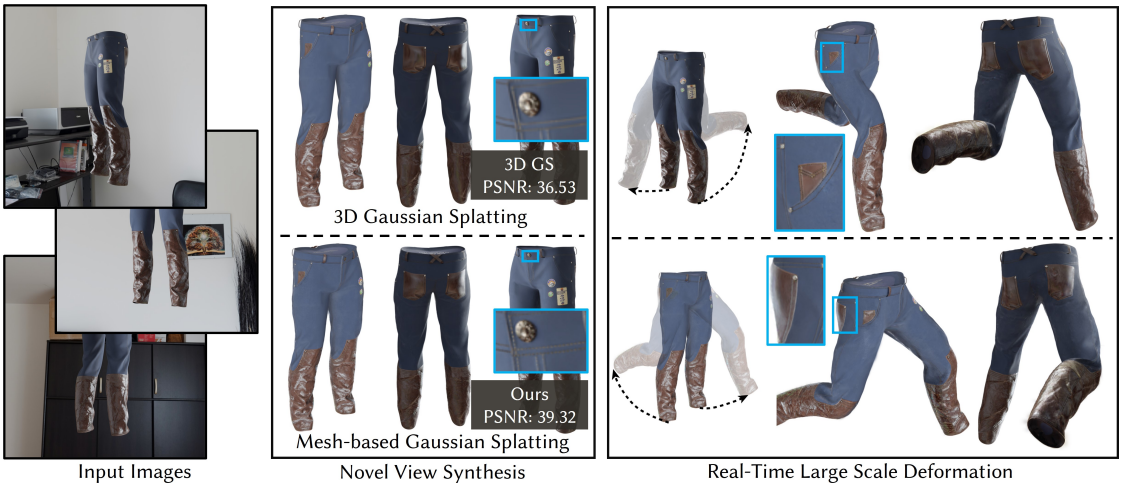
Introduction

최근 몇 년 동안 NeRF, SDF와 같은 implicit한 표현은 몇 개의 멀티뷰 이미지만으로 매우 사실적인 외형과 복잡한 형상을 재구성할 수 있기 때문에 많은 주목을 받았다. 그러나 implicit한 표현에는 느린 렌더링 속도와 같은 본질적인 단점이 있어 실제 응용에 대한 적용 가능성이 제한된다. 장점을 유지하면서 이러한 단점을 극복하기 위해 3DGS(3D Gaussian Splatting)가 제안되었다. 3DGS는 Structure from Motion (SFM) 포인트를 사용하여 초기화한 다음 Gaussian의 공간 분포를 학습한다. 이는 NeRF에서 사용하는 연속적인 표현과 달리 명시적인 개별 3D 장면 표현을 자연스럽게 제공한다. 3DGS는 학습 비용이 적고 미분 가능한 rasterization을 기반으로 고품질의 실시간 렌더링을 달성할 수 있다.

3DGS는 개별 Gaussian을 기반으로 구축되었으므로 해당 Gaussian에 직접 deformation(변형)을 수행하는 것이 자연스러워 보일 수 있다. 그러나 단순한 deformation 방법으로는 최적이 아닌 결과가 나올 수 있다. 예를 들어, SC-GS는 sparse control point들을 학습하여 3D 장면의 역학을 모델링하므로 sparse한 점을 조작하여 모션 변형을 가능하게 한다. 그럼에도 불구하고 sparse control point들을 기반으로 하는 방법은 토폴로지 prior의 부족으로 인해 복잡한 형상이나 deformation에 어려움을 겪는다. 반면에 SuGaR은 약간 더 정교한 파이프라인을 사용한다. Gaussian을 정규화하여 표면에 분산시켜 3DGS 표현에서 명시적인 메쉬를 추출하고 메쉬를 조작하여 3DGS를 편집할 수 있다. 그러나 deformation을 수행할 때 SuGaR은 기존 Gaussian을 더 이상 병합하거나 분할하지 않고 스케일과 회전만 조정하며, 법선과 같은 메쉬 속성도 고려하지 않는다. 이로 인해 특히 대규모 deformation을 수행할 때 아티팩트가 발생하여 메쉬의 모양이 크게 변경될 수 있다. 토폴로지 정보 없이 단순히 Gaussian을 변형하면 대규모 deformation을 수행할 때 강한 오정렬 아티팩트가 생성된다.

본 논문의 방법은 3D Gaussian Splatting에서 고품질 실시간 대규모 deformation을 가능하게 한다. 핵심 아이디어는 Gaussian 학습 및 조작에 통합된 혁신적인 메쉬 기반 Gaussian splatting 표현을 설계하는 것이다. 특히 기존 방법으로 추출된 장면의 메쉬가 주어지면 메쉬와 3DGS 표현을 서로 바인딩한다. 이 바인딩을 활용하여 새로운 방식으로 3DGS 학습과 deformation에 대한 guidance를 제공한다. 3DGS 학습 과정에서 Gaussian 분할은 두 가지 옵션으로 제한된다. 첫 번째는 면을 따라 분할하는 것이며, 두 개의 Gaussian이 표면에 남아 있다. 다른 하나는 법선을 따라 분할하는 것이며, 두 개의 Gaussian이 표면 법선을 따라 정렬된다. 이 접근 방식은 아티팩트로 이어질 수 있는 비합리적인 Gaussian (ex. 잘못 정렬된 Gaussian, 길고 좁은 모양의 Gaussian)을 제거하여 조작을 형성하는 데 도움이 되고 렌더링을 향상시킨다.

저자들은 제안된 메쉬 기반 GS를 기반으로 편집 가능한 GS를 달성하기 위해 메쉬 deformation에 따라 3D Gaussian의 파라미터를 변경하는 대규모 Gaussian deformation 기술을 도입하였다. 특히, 메쉬에 기존 메쉬 deformation 기술을 사용하고 이웃 Gaussian의 파라미터에 deformation gradient를 적용한다. 이 프로세스는 실시간으로 splatting 절차를 통해 직접 렌더링될 수 있다. 이는 mesh-GS 바인딩 덕분에 이전에 메쉬 기반 방법에서만 사용할 수 있었던 직관적인 데이터 기반 deformation을 deformation에 적용할 수 있다. 또한 Gaussian 모양의 공간 연속성과 로컬 합리성을 강화하고 Gaussian deformation에 대한 3D Gaussian의 이방성으로 인한 흐릿한 시각적 아티팩트를 방지하기 위해 정규화 loss가 도입되었다. 마지막으로 저자들은 3D Gaussian의 인터랙티브한 deformation을 가능하게 하기 위해 사용자 친화적인 제약 조건을 준수하면서 실시간 Gaussian 조작과 고품질 splatting을 가능하게 하는 인터랙티브한 도구를 설계하였다.

저자들은 공개 데이터셋과 자체 캡처한 장면에 대한 광범위한 실험을 통해 메쉬 기반 GS가 유망한 렌더링 속도(단일 NVIDIA RTX 4090 GPU에서 평균 65FPS)를 유지하면서 기존 기술에 비해 더 나은 novel view synthesis(NVS)를 달성한다는 것을 입증했다. 본 논문의 방법은 Gaussian splatting의 대규모 deformation이 가능하여 기존 방법보다 성능이 뛰어나다.

Methodology

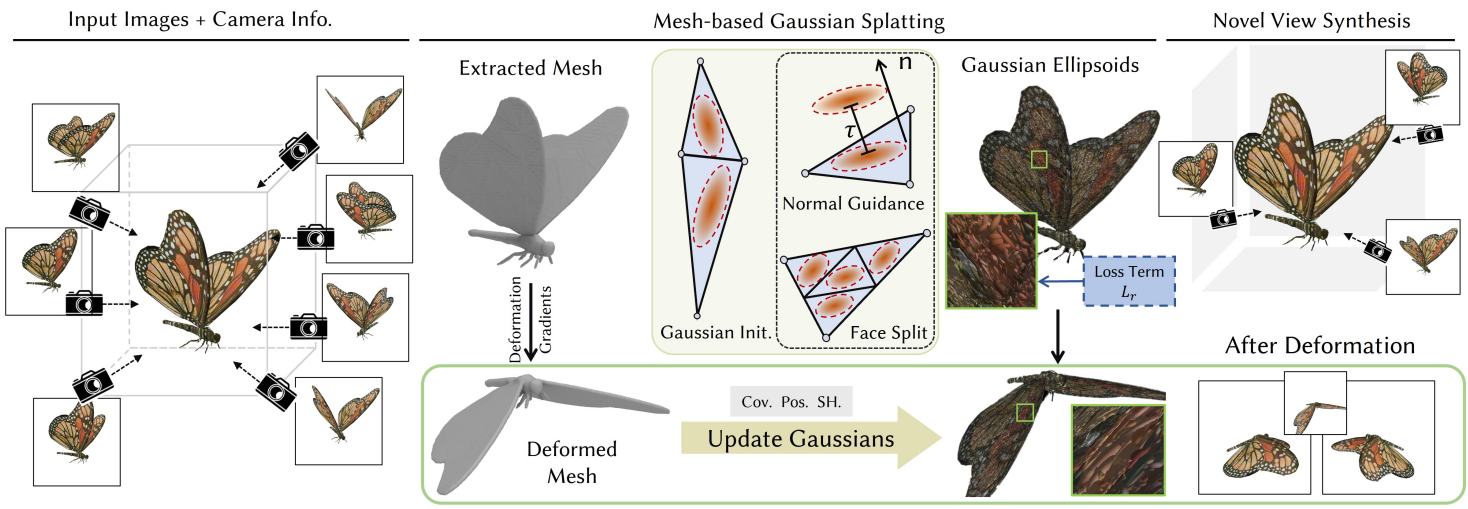
멀티뷰 이미지 모음이 주어지면 장면의 형상과 모양을 기존 접근 방식(ex. NeuS2)으로 추출된 explicit한 메쉬와 결합된 Gaussian으로 표현한다. 본 논문의 목표는 3DGS의 실시간 deformation을 가능하게 하는 것이다. 사실적이고 상호작용적인 deformation을 위해 explicit한 메쉬를 토폴로지 guidance로 도입하고 메쉬 기반 Gaussian 학습을 사용하여 파라미터와 Gaussian 함수의 성장 프로세스를 제한함으로써 3D Gaussian과 기하학적 형태 간의 상관관계를 보장하는 것이다. Gaussian 학습 후 GS와 메쉬의 바인딩 덕분에 사용자가 제어하는 변형된 메쉬의 deformation gradient가 Gaussian 파라미터에 적용된다. 또한 deformation 과정에서 Gaussian의 극심한 이방성을 제거하기 위해 Gaussian 모양의 정규화를 설계했다. 저자들은 이를 실시간 deformation을 위한 인터랙티브한 도구에 통합하여 사용자 제어에 따라 효율적으로 사실적인 새로운 뷰 렌더링을 가능하게 하였다. 파이프라인의 개요는 위 그림에 나와 있다.

1. Preliminaries

Mesh Deformation

삼각형 메쉬 $\mathcal{M}$이 주어지면 기존 메쉬 deformation 방법을 사용하여 사용자의 제어를 만족하는 메쉬를 변형할 수 있다. 이 방법들은 deformation gradient를 최적화하여 대규모 메쉬 deformation을 처리할 수 있다. Deformation은 에너지 함수를 최소화하며 메쉬의 강성을 보장하고 로컬한 왜곡을 방지한다.

\[\begin{equation} \mathcal{E} (\mathcal{M}^\prime) = \sum_{i=1}^N \sum_{j \in \mathcal{N}(i)} w_{ij} \| (\mathbf{v}_i^\prime - \mathbf{v}_j^\prime) - \mathbf{T}_i (\mathbf{v}_i - \mathbf{v}_j) \|^2 \end{equation}\]

여기서 $\mathcal{N}N(i)$는 꼭지점 $i$의 이웃하는 1-ring 꼭지점의 집합, $v_i$는 메쉬 $\mathcal{M}$의 $i$번째 꼭지점의 공간 좌표, \(v_i^\prime\)은 변형된 메쉬 \(\mathcal{M}^\prime\)의 꼭지점의 공간 좌표, $w_{ij}$는 코탄젠트 가중치이다. Transformation matrix $T_i$는 polar decomposition을 통해 rotation matrix \(\bar{\mathbf{R}}_i\)와 shear matrix \(\bar{\mathbf{S}}_i\)로 분해될 수 있다. Deformation 중에 두 행렬 모두 해당 Gaussian에 적용된다. 이 deformation 공식은 이전의 일부 변형된 메쉬를 사용할 수 있는 경우 데이터 기반 deformation도 지원한다. $T_i$는 예시 메쉬의 기존 deformation gradient를 혼합하여 최적화할 수 있다.

2. Mesh-based Gaussian Splatting

3DGS는 사실적인 렌더링 이미지를 실시간으로 생성할 수 있지만 3D 장면의 디테일과 토폴로지 구조를 정확하게 표현하는 데 어려움을 겪는다. 이러한 제한은 특히 deformation과 관련하여 discrete한 Gaussian에 의존하기 때문에 발생한다. 이러한 문제를 해결하기 위해 저자들은 Mesh-based Gaussian Splatting을 도입하였다. 본 논문의 방법은 3D Gaussian을 지정된 메쉬 표면과 통합하여 Gaussian deformation 프로세스를 향상시키는 데 중점을 둔다.

기존의 방법을 사용하여 얻은 재구성된 메쉬 $\mathcal{M}$은 explicit prior로 사용된다. 이는 위 그림에 설명된 것처럼 Gaussian 파라미터와 Gaussian의 성장을 조절하는 두 가지 전략과 결합된다. 이는 3D Gaussian와 explicit prior 간의 상관관계를 보장한다. 이 두 가지 전략의 목적은 3D Gaussian을 정규화하는 동시에 기하학적 특징과 텍스처 특징을 정확하게 표현하는 능력을 유지하는 것이다. 먼저, 메쉬 표면의 모든 삼각형 면의 중심에 정확하게 고정하여 Gaussian을 초기화한다. 원래 3DGS와 다른 메쉬 기반 3DGS를 학습하는 동안 다음 두 공식을 활용하여 Gaussian을 분할한다.

1. Face Split: 하나의 삼각형은 각 변의 중점에 새 꼭지점을 삽입하여 표면 위의 4개의 작은 삼각형으로 세분화된다. Gaussian도 같은 방식으로 분할된다.
2. Normal Guidance: 각 Gaussian은 normal guidance에 따라 표면에 수직으로 움직인다. 이 움직임의 거리 $\tau$는 학습 가능하다.

3D Gaussian은 위의 두 가지 전략에 의해 결정되며, 여기에는 explicit한 mesh prior가 포함된다. Face Split은 메쉬 표면의 guidance에 따라 3D 장면의 시각적 모양을 정확하게 표현하기 위해 충분한 수의 Gaussian을 보장하는 것이다. Normal Guidance는 NVS를 위한 3D 장면의 세밀한 텍스처 디테일을 표현하는 것을 목표로 한다. 둘 다 사전에 explicit한 표면 근처의 Gaussian을 필요로 한다. Reduction 연산은 원래 3DGS를 따른다.

따라서 무게중심 좌표 $w = (w_a, w_b, w_c)$와 오프셋 거리 $\tau$는 3DGS 학습을 위한 추가 속성으로 parameterize된다. 무게 중심 좌표 $(w_a, w_b, w_c)$는 인접한 삼각형의 세 개의 꼭지점 \((\mathbf{v}_a, \mathbf{v}_b, \mathbf{v}_c)\)에 할당된 가중치를 나타내며, $\tau \in [-0.5, 0.5]$는 표면 법선 $\mathbf{n}$을 따른 변위(displacement)이다. 요약하면, Gaussian의 공간적 위치 $\mu$는 다음과 같다.

\[\begin{equation} \mu = (w_a \mathbf{v}_a + w_b \mathbf{v}_b + w_c \mathbf{v}_c) + \tau R \mathbf{n} \end{equation}\]

여기서 $R$은 인접한 삼각형의 외접원의 반지름이다. Explicit한 메쉬의 prior를 활용하여 explicit한 표면에 따라 Gaussian 밀도를 정규화하고 새로운 Gaussian을 생성한 다음 최적화에 사용할 수 있다.

Regularization

변형된 3DGS의 더 나은 시각적 품질을 위해 정규화를 도입하여 Gaussian의 공간적 일관성과 로컬 일관성을 보장한다. 임의의 deformation을 지원하기 때문에 대규모 deformation으로 인해 로컬 메쉬가 급격한 변화를 겪을 수 있는 것은 불가피하다. 학습된 Gaussian 모양이 충분히 크고 표면의 여러 삼각형을 덮는 경우 3D Gaussian의 이방성으로 인해 시각적 아티팩트가 발생한다. 그럴듯한 deformation 결과를 보장하기 위해 학습 중에 인접한 삼각형의 크기를 기반으로 Gaussian 모양을 조정하는 정규화 $L_r$을 사용한다. 이를 통해 deformation 중에 적절한 Gaussian가 학습되고 로컬 연속성이 유지된다. 정규화 $L_r$은 다음과 같다.

\[\begin{equation} L_r = \sum_{g \in G} \max (\max (s_i) - \gamma R_i, 0) \end{equation}\]

여기서 $s_i$는 각 Gaussian의 3D scaling 벡터이고, $R_i$는 Gaussian이 위치한 삼각형의 외접원의 반지름이며, $\gamma$는 인접한 삼각형이 Gaussian 크기에 미치는 영향을 제어하기 위한 hyperparameter이다.

3. Editable Gaussian with Mesh Deformation

기존 메쉬 deformation 방법을 활용하고 GS의 효율적인 미분 가능한 rasterization을 활용하면 GS 표현을 기반으로 Gaussian의 실시간 deformation을 달성하는 것이 가능하다. 이 아이디어를 설명하기 위해 앞서 설명한 메쉬 deformation 기술과 공식을 사용한다. 사용자는 non-rigid deformation, translation, rotation 등과 같은 다양한 컨트롤을 사용하여 3D Gaussian을 조작할 수 있다. 변형된 메쉬 $\mathcal{M}$의 각 꼭지점 $v_i$는 해당 꼭지점 주위의 로컬 변화를 나타내는 transformation matrix $T_i$에 연결되어 있다. $T_i$는 변형된 메쉬 $\mathcal{M}^\prime$과 원래 메쉬 $\mathcal{M}$ 사이의 행렬이며 polar decomposition을 사용하여 rotation matrix \(\bar{\mathbf{R}}_i\)와 shear matrix \(\bar{\mathbf{S}}_i\)로 분해될 수 있다. Affine transformation 후에도 Gaussian이 변경되지 않기 때문에 변형된 메쉬의 \(\bar{\mathbf{R}}_i\)와 \(\bar{\mathbf{S}}_i\)를 관련된 Gaussian뿐만 아니라 변형된 메쉬 면의 변위에도 쉽게 적용할 수 있다.

변형된 각 Gaussian $g^\prime$은 3개의 변형된 꼭지점을 갖는 삼각형 \(f^\prime = (\mathbf{v}_a^\prime, \mathbf{v}_b^\prime, \mathbf{v}_c^\prime)\)로 묶여 있다. 변형된 면에 대한 상대적 변위 $\Delta P$와 deformation gradient $T_i$는 무게중심 좌표 $(w_a, w_b, w_c)$를 사용하여 표현될 수 있다.

\[\begin{aligned} \Delta P &= w_a (\mathbf{v}_a^\prime - \mathbf{v}_a) + w_b (\mathbf{v}_b^\prime - \mathbf{v}_b) + w_c (\mathbf{v}_c^\prime + \mathbf{v}_c) \\ \bar{\mathbf{R}}_i &= w_a \log (\bar{\mathbf{R}}_{\mathbf{v}_a^\prime}) + w_b \log (\bar{\mathbf{R}}_{\mathbf{v}_b^\prime}) + w_c \log (\bar{\mathbf{R}}_{\mathbf{v}_c^\prime}) \\ \bar{\mathbf{S}}_i &= w_a \bar{\mathbf{S}}_{\mathbf{v}_a^\prime} + w_b \bar{\mathbf{S}}_{\mathbf{v}_b^\prime} + w_c \bar{\mathbf{S}}_{\mathbf{v}_c^\prime} \\ T_i &= \exp (\bar{\mathbf{R}}_i) \bar{\mathbf{S}}_i \end{aligned}\]

위 방정식에 따라 위치 $\mu^\prime = \mu + \Delta P$와 공분산 행렬 $\Sigma^\prime = T_i \Sigma T_i^\top$를 갖는 변환된 Gaussian을 얻을 수 있다. 변형된 Gaussian은 다음과 같다.

\[\begin{equation} g^\prime (x) = \exp (-\frac{1}{2} (x - (\mu + \Delta P))^\top (T_i \Sigma T_i^\top)^{-1} (x - (\mu + \Delta P))) \end{equation}\]

또한 3DGS는 spherical harmonics(SH)를 사용하여 색상을 표현하는데, 주어진 Gaussian은 각도에 따라 다양한 색상을 나타내므로 뷰에 따른 모델링이 가능하다. 따라서 변형된 Gaussian $g^\prime$의 경우 변형된 메쉬의 rotation matrix \(\exp (\bar{\mathbf{R}}_i)\)의 역행렬을 뷰 방향 $d$에 적용하여 SH의 방향을 조정해야 한다.

\[\begin{equation} \textrm{SH} (\exp (\bar{\mathbf{R}}_i)^\top d, c_i) \end{equation}\]

결론적으로, 메쉬 기반 GS 표현을 사용하면 메쉬 deformation을 통해 Gaussian을 유연하게 조작할 수 있으며 충실도가 높은 렌더링으로 새로운 뷰를 얻을 수 있다.

Experiments

• 데이터셋: NeRF-Synthetic, SketchFab의 합성 데이터, 자체적으로 캡처한 현실 장면

1. Comparisons & Evaluations

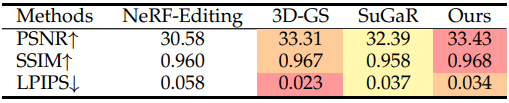
다음은 NeRF-Synthetic 데이터셋에서의 NVS 성능을 비교한 표이다.

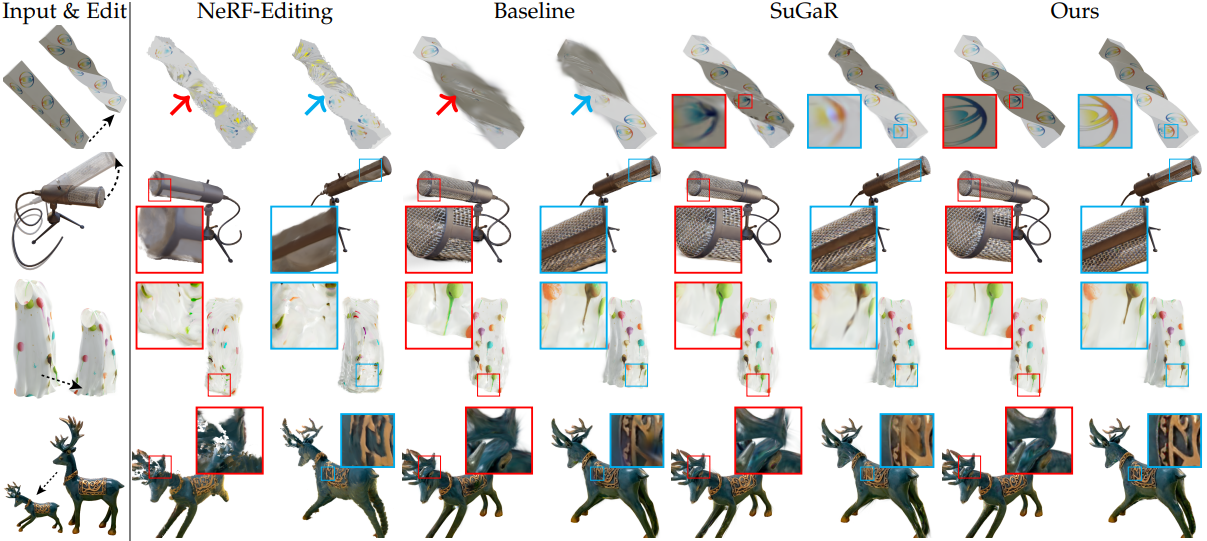
다음은 기존 방법들과 deformation 결과를 비교한 것이다.

2. More Deformation Results

다음은 deformation 결과들이다.

3. Ablations

다음은 Face Split과 정규화 $L_r$에 대한 ablation 결과이다.

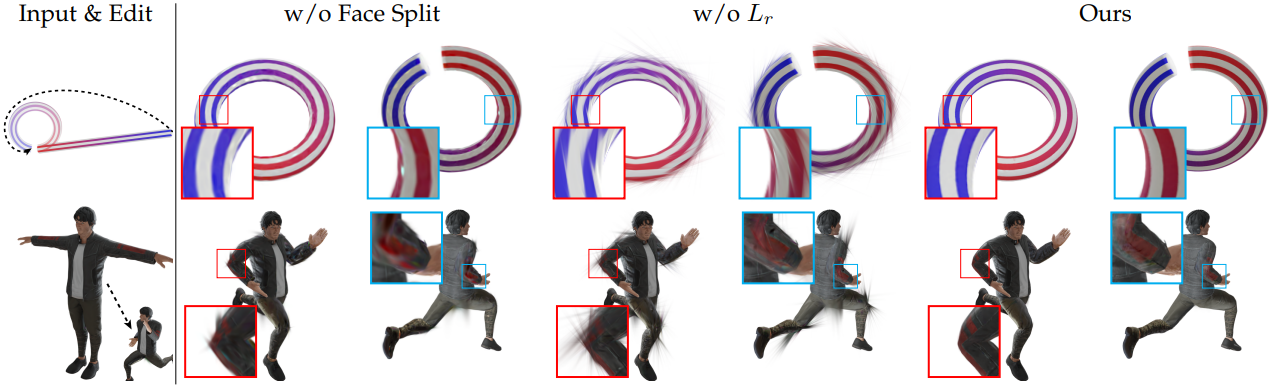
다음은 Normal Guidance에 대한 ablation 결과이다.

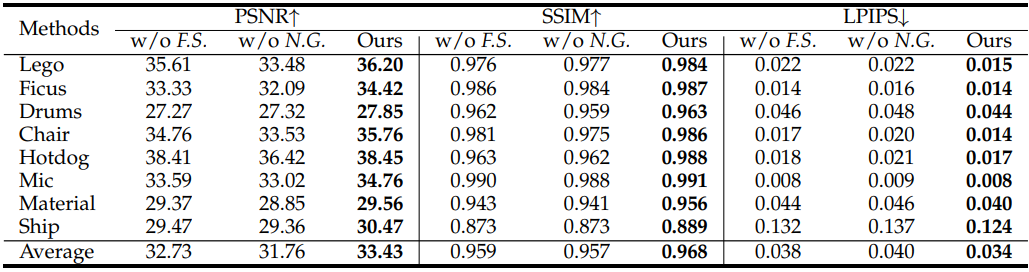
다음은 메쉬 해상도에 대한 ablation 결과이다.

Limitations

1. 시각적 외형과 그림자는 편집할 수 없다.
2. 이 방법은 추출된 메쉬에 의존하므로 복잡한 투명 물체와 같이 메쉬를 추출할 수 없는 경우 실패한다.