[논문리뷰] Memento: Fine-tuning LLM Agents without Fine-tuning LLMs
arXiv 2025. [Paper] [Github]
Huichi Zhou, Yihang Chen, Siyuan Guo, Xue Yan, Kin Hei Lee, Zihan Wang, Ka Yiu Lee, Guchun Zhang, Kun Shao, Linyi Yang, Jun Wang
UCL | Huawei Noah’s Ark Lab | Jilin University | CAS
22 Aug 2025
Introduction
현재 LLM 에이전트는 일반적으로 두 가지 패러다임을 따르며, 각각 근본적인 한계를 보인다. 첫 번째 패러다임은 고정된 워크플로와 하드코딩된 추론을 기반으로 특수 프레임워크를 구축하는데, 이는 제한된 task에는 효과적이지만 유연성이 부족하다. 이러한 에이전트는 배포 후 온라인 정보를 통합하거나 새로운 상황에 적응하지 못한다. 두 번째 패러다임은 supervised fine-tuning (SFT) 또는 강화 학습(RL)을 통해 LLM 자체를 업데이트하는 데 중점을 둔다. 이는 더욱 유연한 동작을 가능하게 하지만 높은 계산 비용을 초래한다. 이러한 접근법은 지속적인 적응과 온라인 학습에 비효율적이며, 개방형 시나리오에 배포된 에이전트에는 비실용적이다.
본 논문은 기본 LLM을 수정하지 않고도 지속적인 적응을 가능하게 하는 메모리 기반 학습 프레임워크를 제안함으로써 이러한 과제를 해결하였다. LLM 에이전트는 기본 모델을 fine-tuning하는 대신 외부 메모리를 활용하여 성공 및 실패 레이블을 포함한 과거 궤적을 저장하고 유사한 과거 경험을 바탕으로 의사 결정을 가이드한다.
이러한 접근 방식은 case-based reasoning (CBR)의 원칙과 일치한다. 예를 들어, 심층 연구 시나리오에서 이전에 웹 기반 task에 성공한 에이전트는 자신의 경험을 활용하여 이전에는 경험해보지 못했던 구조적으로 유사한 task를 해결할 수 있다. 본 방법은 심층 연구 에이전트에게 효율적이고 일반화 가능하며 인간의 학습 방식에서 영감을 받은 새로운 지속적 학습 경로를 제공한다.
이를 위해, CBR을 위한 non-parametric하고 즉석에서 학습하는 프레임워크인 Memento를 소개한다. 이 프레임워크는 메모리 기반 MDP (M-MDP)에 기반한 planner-executor 아키텍처로 구현되며, planner, 도구 기반 executor, 과거 궤적을 에피소드 메모리로 저장하는 확장형 case bank로 구성된다. Memento의 온라인 CBR은 학습 후 고정되는 LLM의 parametric한 메모리에만 의존하는 대신, 풍부한 에피소드 추적을 저장하여 구현된다.
Methodology: Memory-Based MDP with Case-based Reasoning Policy
본 논문에서는 LLM 에이전트를 Case-Based Reasoning (CBR)과 통합하였다. CBR은 기존에 경험했던 유사 문제의 해결책을 학습하여 새로운 문제를 해결하는 고전적인 문제 해결 패러다임이다. 따라서 LLM 에이전트는 메모리에 저장된 경험을 통해 학습함으로써 파라미터 fine-tuning 없이도 지속적인 개선을 달성할 수 있다.
먼저, CBR 에이전트의 순차적 의사 결정 과정을 Memory-Based Markov Decision Process (M-MDP)으로 모델링한다.
Memory-Based Markov Decision Process (M-MDP)
M-MDP는 튜플 $\langle \mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma, \mathcal{M} \rangle$이며, $\mathcal{S}$는 state space, $\mathcal{A}$는 action space, $\mathcal{P} : \mathcal{S} \times \mathcal{A} \rightarrow \Delta (\mathcal{S})$는 transition dynamics, $\mathcal{R} : \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}$은 reward function, $\gamma \in [0, 1)$은 discount factor, $\mathcal{M} = (\mathcal{S} \times \mathcal{A} \times \mathbb{R})$은 memory space이다.
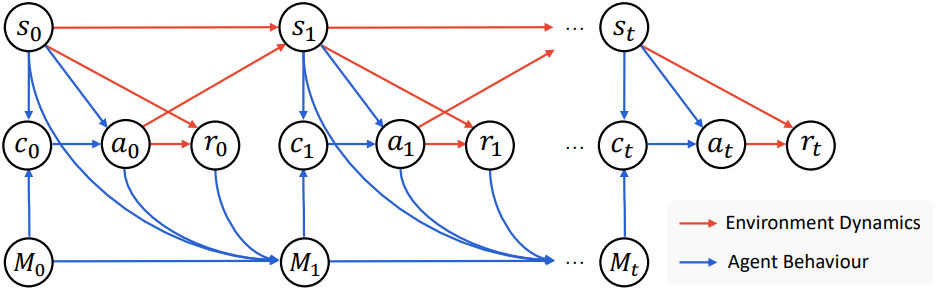
표준 MDP와의 주요 차이점은 memory space를 과거 경험의 집합으로 정의한다는 것이다. CBR 에이전트의 경우, state space와 action space는 모두 미리 정의된 vocabulary $\mathcal{V}에 대한 모든 유한 길이 시퀀스의 집합으로 정의된다.
M-MDP를 사용하면 CBR 에이전트의 동작을 설명할 수 있다. Timestep $t$에서 case bank \(M_t = \{c_i = (s_i, a_i, r_i)\}_{i=1}^{N_t}\)를 유지한다. 현재 state $s_t$가 주어지면 CBR 에이전트는 먼저 케이스 $c_t$를 검색한 다음 LLM을 통해 재사용하고 조정한다.
\[\begin{equation} c_t \sim \mu(\cdot \vert s_t, M_t) \\ a_t \sim p_\textrm{LLM} (\cdot \vert s_t, c_t) \end{equation}\]($\mu$는 케이스 검색 policy)
Action $a_t$를 수행하면 CBR 에이전트는 reward $r_t = \mathcal{R}(s_t, a_t)$를 받고 다음 state $s_{t+1} \sim \mathcal{P}(\cdot \vert s_t, a_t)$를 관찰한다. CBR 에이전트는 새로운 케이스를 case bank에 유지한다.
\[\begin{equation} M_{t+1} = M_t \cup \{(s_t , a_t ,r_t)\} \end{equation}\]Case-Based Reasoning (CBR) Agent
CBR 에이전트는 현재 state와 과거 경험에 대한 유한한 메모리를 기반으로 결정을 내리는 에이전트이다. CBR 에이전트의 전체 policy $\pi$는 다음과 같이 정의된다.
\[\begin{equation} \pi(a \vert s, M) = \sum_{c \in M} \mu (c \vert s, M) p_\textrm{LLM} (a \vert s, c) \end{equation}\]전반적으로 CBR 에이전트의 궤적 $\tau$는 다음과 같이 나타낼 수 있다.
\[\begin{equation} τ = \{M_0, s_0, c_0, a_0, r_0, M_1, s_1, c_1, a_1, r_1, \cdots\} \end{equation}\]궤적 $\tau$를 샘플링할 확률은 다음과 같이 모델링할 수 있다.
\[\begin{equation} p(\tau) = \prod_{t=0}^{T-1} \underbrace{\mu (c_t \vert s_t, M_t)}_{\textrm{Retrieve}} \underbrace{p_\textrm{LLM} (a_t \vert s_t, c_t)}_{\textrm{Reuse & Revise}} \underbrace{\mathbb{I}(r_t = \mathcal{R}(s_t, a_t))}_{\textrm{Evaluation}} \underbrace{\mathbb{I}(M_{t+1} = M_t \cup (s_t, a_t, r_t))}_{\textrm{Retain}} \underbrace{\mathcal{P} (s_{t+1} \vert s_t, a_t)}_{\textrm{Transition}} \end{equation}\]($\mathbb{I}(\cdot)$는 indicator function, $T$는 최대 궤적 길이)
Retrieve, Reuse & Revise, Retain은 에이전트 행동을 설명하며, Evaluation과 Transition은 environment dynamics를 모델링한다.
Soft Q-Learning for CBR Agent
CBR policy $\pi$를 최적화하기 위해, LLM을 고정하고 케이스 검색 policy $\mu$를 학습하는 것을 목표로 한다. $\mu$의 action은 case bank $M$에서 케이스 $c = (s, a, r)$을 선택하는 것이다. 검색된 케이스의 다양성을 높이는 동시에 최적화하기 위해, maximum entropy 프레임워크를 적용하고 다음과 같은 최적화 objective를 도출한다.
\[\begin{equation} J(\pi) = \mathbb{E}_{\tau \sim p} \left[ \sum_{t=0}^{T-1} [\mathcal{R}(s_t, a_t) + \alpha \mathcal{H} (\mu (\cdot \vert s_t, M_t))] \right] \end{equation}\]($H$는 엔트로피)
이 프레임워크에서 value function은 다음과 같이 정의할 수 있다.
\[\begin{equation} V^\pi (s_t, M_t) = \sum_{c \in M_t} \mu (c \vert s_t, M_t) [Q^\pi (s_t, M_t, c) - \alpha \log \mu (c \vert s_t, M_t)] \end{equation}\]또한, state가 주어졌을 때 action, 즉 케이스 선택을 취하기 위한 Q value function은 다음과 같이 정의할 수 있다.
\[\begin{equation} Q^\pi (s_t, M_t, c_t) = \mathbb{E}_{a \sim p_\textrm{LLM}(\cdot \vert s_t, c_t), s_{t+1} \sim \mathcal{P}(\cdot s_t, a_t)} [\mathcal{R}(s_t, a_t) + \gamma V^\pi (s_{t+1}, M_{t+1})] \end{equation}\]$d^\pi (s, M) = \sum_{t=0}^\infty \gamma^{t-1} \mathbb{P} (s_t = s, M_t = M)$을 $\pi$ 하에서 $(s, M)$의 discount된 방문 빈도라 하면, objective는 다음과 같이 정의된다.
\[\begin{aligned} J(\pi) &= \mathbb{E}_{(s, M) \sim d^\pi} [V^\pi (s, M)] \\ &= \mathbb{E}_{(s, M) \sim d^\pi} \left[ \sum_{c \in M} \mu (c \vert s, M) [Q^\pi (s, M, c) - \alpha \log \mu (c \vert s, M)] \right] \end{aligned}\]그러면 최적 Q value에 대한 softmax로 최적 검색 policy의 closed-form solution을 도출할 수 있다.
\[\begin{equation} \mu^\ast (c \vert s, M) = \frac{\exp (Q^\ast (s, M, c) / \alpha)}{\sum_{c^\prime \in M} \exp (Q^\ast (s, M, c^\prime) / \alpha)} \end{equation}\]이런 방식으로, Q-function $Q$를 학습하여 최적의 검색 policy를 도출할 수 있으며, 이는 soft Q-learning에서 temporal difference (TD) learning을 통해 다음과 같이 달성할 수 있다.
\[\begin{equation} Q(s_t, M_t, c_t) \leftarrow Q(s_t, M_t, c_t) + \eta \left[ r_t + \gamma \alpha \log \sum_{c^\prime \in M_{t+1}} \exp (Q(s_{t+1}, M_{t+1}, c_{t+1})) - Q(s_t, M_t, c_t) \right] \end{equation}\]($\eta$는 learning rate)
Enhance Q-Learning Based on State Similarity
TD learning을 통해 Q-function을 처음부터 학습할 수 있다. 그러나 Q-function을 직접 학습하는 것은 state와 케이스 설명이 자연어 형태로 표현되기 때문에 어렵다. 이를 위해 episodic control (EC) 알고리즘에 따라 커널 기반 추정을 통해 Q value를 근사한다. 구체적으로, state, 검색된 케이스, 그리고 각 상호작용의 Q value를 포함하는 에피소드 메모리 \(\mathcal{D} = \{(s, c, Q)\}\)를 유지한다. 그런 다음, $\theta$로 parametrize된 커널 네트워크 $k_\theta$를 통해 Q-function을 근사한다.
\[\begin{equation} Q_\textrm{EC} (s, M, c; \theta) = \sum_{(s^\prime, c^\prime, Q^\prime) \in \mathcal{D}_c} \frac{k_\theta (s, s^\prime) Q^\prime}{\sum_{(\hat{s}, \hat{c}, \hat{Q}) \in \mathcal{D}_c} k_\theta (s, \hat{s})} \\ \textrm{where} \quad \mathcal{D}_c = \{(s_i, c_i, Q_i) \in \mathcal{D} : c_i = c\} \end{equation}\](\(\mathcal{D}_c\)는 동일한 검색된 케이스 $c$와 에피소드 메모리 $\mathcal{D}$에 저장된 과거 상호 작용)
위 식을 TD learning 식에 TD learning을 통해 커널 파라미터 $\theta$를 최적화하여 Q-function을 학습시킬 수 있다.
\[\begin{equation} \mathcal{L}(\theta) = \mathbb{E}_{(s, c, r, s^\prime, M, M^\prime)} \left[ \left( Q_\textrm{EC} (s, M, c; \theta) - [r + \gamma \alpha \log \sum_{c^\prime \in M^\prime} \exp (Q_\textrm{EC} (s^\prime, M^\prime, c^\prime; \bar{\theta}))] \right)^2 \right] \end{equation}\](\(\bar{\theta}\)는 타겟 커널 네트워크, $s^\prime$은 다음 state, \(M^\prime = M \cup \{c\}\)은 업데이트된 case bank)

Implementation: Deep Research Agent
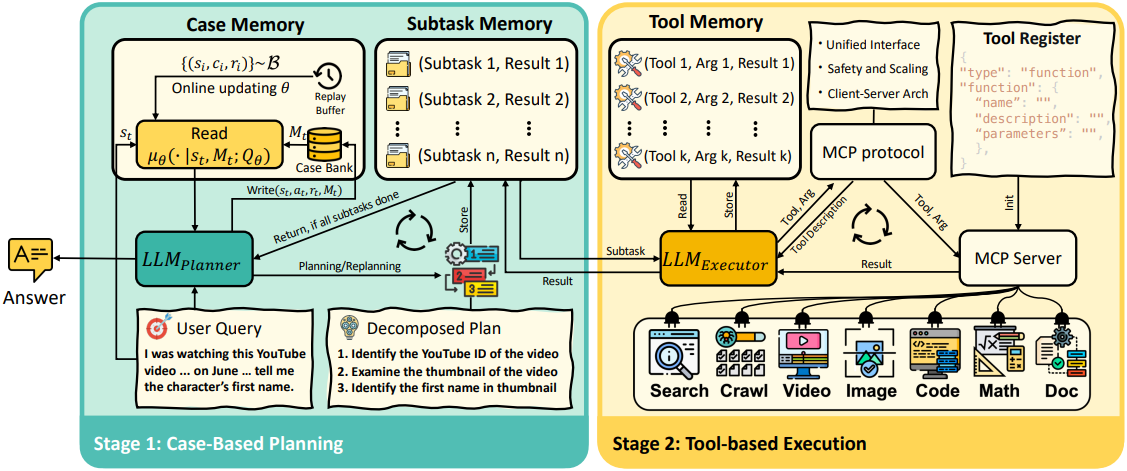
저자들은 심층 연구 시나리오에서 M-MDP 방법론을 통해 state 기반 프롬프트 엔지니어링을 구현하였다. 이 시나리오에서 에이전트는 environment와 반복적으로 상호작용하고, 외부 도구를 호출하고, 외부 소스에서 정보를 검색하고, 동적 추론을 위해 다양한 데이터를 처리하여 복잡하고 장기적인 task를 해결해야 한다. 위 그림에서 볼 수 있듯이, Memento는 Case-Based Planning과 Tool-Based Execution이라는 두 가지 핵심 단계를 번갈아 수행한다.
1. Framework
장기적 추론의 어려움을 해결하기 위해 Memento는 plan-and-act 패러다임을 따른다. 이 패러다임에서는 Planner와 Executor가 교대로 순환하며 task를 반복적으로 진행한다. 효과적인 조정을 위해 Memento는 세 가지 메모리 모듈을 통합하였다.
- Case Memory: 고수준 planning을 위한 이전 케이스의 벡터화된 데이터
- Subtask Memory: subtask와 그 결과를 텍스트 기반으로 저장
- Tool Memory: 각 subtask에 대한 도구 상호작용의 텍스트 기반 로그
Planning 단계에서 LLM 기반 CBR 에이전트인 Planner는 task instruction를 받고 case memory를 쿼리하여 관련 케이스 트리플렛 \((s_i, a_i, r_i)_{i=1}^K\)을 반환한다 ($s_i$는 task, $a_i$는 계획, $r_i$는 성공 여부, $K$는 검색 횟수). 이 프로세스는 유사성 기반 검색기 또는 온라인으로 업데이트되는 Q-function을 통해 case bank에서 관련 경험을 검색하는 Case Memory 모듈의 지원을 받아 Planner가 활용할 수 있도록 한다. 검색된 케이스는 현재 task instruction과 concat되어 프롬프트를 형성하고 LLM이 각 subtask에 대한 계획을 생성하도록 가이드한다.
초기 task가 분해되면 subtask memory 모듈이 Planner와 Executor 간의 상호 작용을 조정하여 생성된 subtask와 실행 결과를 기록한다. 각 iteration 후에 Planner는 누적된 실행 기록을 사용하여 task 완료를 평가한다. Task가 완료되지 않은 경우 Planner는 업데이트된 컨텍스트에 따라 다시 계획을 세운다. 그렇지 않은 경우 최종 결과가 반환되고, task 완료 시에만 case memory가 새로운 경험으로 업데이트된다.
Execution 단계는 범용 LLM으로 구동되는 Executor에 의해 관리되며, MCP 프로토콜을 사용하여 각 subtask를 자율적인 에피소드로 실행한다. 기존 에이전트들과 달리 Memento의 Executor는 풍부한 추론과 유연한 도구 조합을 지원한다. 각 subtask에 대해 Executor는 tool memory를 참조하여 적절한 도구 호출을 결정하고 결과를 업데이트한다. 이는 MCP 클라이언트로 작동한다. Executor는 subtask memory에서 보류 중인 subtask를 읽고, tool memory에서 관련 기록에 액세스하고, 외부 도구를 호출할지 또는 결과를 반환할지 결정한다. MCP는 표준화되고 모델에 독립적인 인터페이스 역할을 하여 다양한 외부 도구 및 데이터 소스와 유연하게 조정할 수 있다. Memento는 하나의 프로토콜 레이어에서 액세스를 통합함으로써 여러 도메인에서 동적 추론 및 여러 도구 사용을 원활하게 통합할 수 있다.
2. Case Memory Management
Case memory는 Write 연산과 Read 연산으로 운영되는 case bank $M_t$이며, non-parametric 버전과 parametric 버전이 존재한다. Non-parametric 버전에서 Write는 단순히 $(s_t, a_t, r_t)$를 추가하고, Read는 계산 효율성을 위해 유사도를 기준으로 케이스를 검색한다. Parametric 버전의 경우 Write는 검색 분포를 형성하기 위해 Q-function을 온라인에서 추가로 업데이트하는 반면, Read는 학습된 Q-function을 기반으로 작동하여 적응적으로 케이스를 선택한다.
Memory Storage
Write 연산은 각 timestep $t$ 후에 각 과거 케이스 $(s_t, a_t, r_t)$를 case bank $M_t$에 추가한다.
\[\begin{equation} \textrm{Write}(s_t, a_t, r_t, M_t) = M_{t+1} = M_t \cup \{(s_t, a_t, r_t)\} \end{equation}\]이 과정에서 state $s_t$는 고정 텍스트 인코더를 사용하여 인코딩되는 반면, action $a_t$와 reward $r_t$는 원래 형태로 보존된다. 이는 state 표현만 후속 검색 연산을 위해 벡터화가 필요하기 때문이다. 이 Write 연산은 에이전트 실행 과정 전반에 걸쳐 지속적으로 수행되므로, case bank는 점진적으로 포괄적인 경험 저장소로 성장할 수 있다. 성공과 실패를 모두 축적함으로써, 메모리는 과거 실수를 정보에 기반하여 회피하기 위한 회고적 분석을 가능하게 할 뿐만 아니라, 미래 계획을 위한 성공적인 경로를 제공한다.
Non-Parametric Memory Retrieval
Memento의 핵심은 진화하는 case bank로, 지속적인 학습 능력을 뒷받침한다. 각 planning 단계에서 이 non-parametric 메모리 모듈은 task instruction을 받은 후 성공 케이스와 실패 케이스가 혼합된 관련 케이스들을 검색한다. 구체적으로, 현재 state와 과거 state 간의 의미적 유사도를 계산하여 case bank에서 가장 가까운 $K$개의 과거 케이스를 검색한다. 이 디자인은 유사한 문제는 유사한 해결책을 가져야 한다는 CBR 패러다임을 따르며, 이를 통해 에이전트는 현재 task와 가장 잘 부합하는 과거 컨텍스트를 가진 케이스에 우선순위를 부여할 수 있다. Non-parametric 메모리의 Read 연산자는 다음과 같이 정의된다.
\[\begin{equation} \textrm{Read}_\textrm{NP} (s_t, M_t) = \underset{(s_i, a_i, r_i) \in M_t}{\textrm{TopK}} \textrm{sim} (\textrm{enc}(s_t), \textrm{enc}(s_i)) \end{equation}\]($s_t$와 $M_t$는 각각 timestep $t$에서의 query bank와 case bank, $\textrm{enc}(\cdot)$는 사전 학습된 텍스트 인코더, $\textrm{sim}(\cdot)$은 코사인 유사도 함수)
Parametric Memory Retrieval
에이전트가 과거 경험으로부터 유용성이 높은 케이스를 선택적으로 활용할 수 있도록 하기 위해, 저자들은 Memento에서 parametric Q-function을 통한 미분 가능한 메모리 메커니즘을 설계하였다. Case bank에 새로운 케이스를 쓸 때, 단순히 튜플을 추가하는 non-parametric 메모리와 달리 parametric한 방법은 Q-function을 온라인으로 동시에 업데이트한다.
한편, Memento에서 planning에만 CBR을 적용하면 CBR Planner를 multi-step M-MDP 대신 single-step으로 단순화할 수 있다. 이 single-step 설정은 TD target을 reward $r$로 축소하여 학습 loss를 단순화한다. 업데이트는 고정되지 않은 target을 피하는 supervised learning 패러다임으로 축소된다. 따라서 커널 기반 추정을 없애고 parametric Q-function $Q(s, c; \theta)$를 end-to-end로 학습할 수 있다. 따라서 single-step Q-learning loss는 다음과 같다.
\[\begin{equation} \mathcal{L}(\theta) = \mathbb{E}_{(s,c,r)} [(Q(s, c; \theta) - r)^2] \end{equation}\]튜플 \(\{(s, c, r)\}\)은 replay buffer $\mathcal{B}$에 저장되고 $Q$는 신경망으로 구현된다. 심층 연구 task의 reward 신호가 0 또는 1임을 고려하여, MSE loss를 cross-entropy (CE) loss로 대체한다. MSE loss는 0/1 근처에서 기울기가 사라지는 문제가 있는 반면, CE loss는 수치적으로 더 안정적인 신호를 제공하기 때문이다.
\[\begin{equation} \mathcal{L}(\theta) = \mathbb{E}_{(s,c,r)} [-r \log Q(s, c; \theta) - (1-r) \log (1 - Q(s, c; \theta))] \end{equation}\]여기서 $Q$는 확률 $p(r = 1 \vert s, c; \theta)$를 나타내는 정규화된 값으로 볼 수 있다. 즉, 주어진 case bank $M$에 대하여 검색된 케이스 $c$가 현재 state $s$에 대한 좋은 레퍼런스일 likelihood이다. 새로운 케이스만 보존하는 non-parametric 메모리와 달리, parametric 메모리는 Write 중에 Q-function을 개선하여 각 업데이트에서 새로운 케이스를 기록하고 전체 Q value 환경을 업데이트할 수 있다.
검색 과정에서 학습된 Q-function은 softmax를 통해 검색 policy 분포를 계산하는 데 사용되며, 이 분포를 기반으로 케이스를 샘플링할 수 있다. 케이스 선택의 무작위성을 줄이고 에이전트의 의사결정 과정에 대한 해석 가능성을 높이기 위해, parametric 메모리의 Read 연산은 TopK 연산자를 적용하여 가장 높은 Q-value를 가진 $K$개의 케이스를 선택하고, 이를 계획의 레퍼런스로 사용한다.
\[\begin{equation} \textrm{Read}_\textrm{P} (s_t, M_t) = \underset{c_i \in M_t}{\textrm{TopK}} \; Q (s_t, c_i; \theta) \end{equation}\]Q-function을 새로운 샘플로 지속적으로 업데이트함으로써 parametric 메모리 모듈은 state와 케이스 간의 latent 패턴을 포착하는 방법을 학습하여 케이스 검색 policy $\mu^\ast$의 분포에 더 가까운 근사값을 생성한다.
3. Tool Usage
심층 연구 task는 긴 실행 시퀀스와 멀티턴 상호작용이 요구되는 것 외에도, 에이전트가 외부 정보를 수집하고 이를 처리, 통합, 분석할 수 있어야 하기 때문에 원자적(atomic) action에 대해서도 엄격한 요구를 제기한다. 따라서 저자들은 MCP 프로토콜을 통해 접근 가능한 Memento 도구 모음을 설계하였다. 여기에는 검색 엔진과 웹 크롤러와 같은 정보 검색 모듈과 다양한 형식의 파일을 처리하고 분석하는 구성 요소들도 포함된다.
외부 정보 수집
최신 외부 지식에 대한 접근이 필요한 개방형 task를 지원하기 위해, 저자들은 검색 및 콘텐츠 수집 기능을 모두 통합하는 검색 툴킷을 설계했다. 구체적으로, Google, Bing, Duckduckgo, Brave 등 여러 소스의 결과를 집계하는 메타서치 엔진인 searxng를 사용하였다. 검색된 후보는 쿼리 컨텍스트와의 의미적 유사성을 기반으로 순위가 재지정되어 관련성과 정확성을 보장한다. 이를 보완하기 위해 Executor가 심층적인 이해가 필요할 경우, Crawl4AI를 통합하여 선택된 결과의 전체 웹 콘텐츠를 가져오고 파싱한다.
다양한 형태의 멀티모달 정보 처리
다양한 형태의 데이터 소스에 대한 다운스트림 추론을 지원하기 위해, 저자들은 다양한 파일 유형과 모달리티에서 정보를 자동으로 추출하는 문서 처리 툴킷을 구현했다.
- 이미지: VLM을 사용하여 캡션을 추가
- 동영상: VLM을 사용하여 텍스트로 요약
- 오디오: 자동 음성 인식을 통해 텍스트화
- PowerPoint 파일: 이미지 설명이 포함된 슬라이드별로 파싱
- 스프레드시트: 읽기 쉬운 행 단위 레이아웃으로 변환
- Word 문서: 마크다운으로 변환
- 압축 파일: 압축 해제
- 일반 텍스트 및 코드 파일: 직접 읽음
- JSON, XML: 구조화된 객체로 파싱
- PDF 또는 지원되지 않는 형식: Chunkr AI를 통한 추출 또는 일반 텍스트 파싱을 사용
추론
추론 및 분석 툴킷은 코드 실행과 수학적 계산을 통합하여 Memento 프레임워크 내에서 강력하고 자동화된 분석을 지원한다. 코드 도구는 통합된 workspace 내에서 코드를 작성, 실행, 관리할 수 있는 샌드박스 환경을 제공한다. 사용자는 task 디렉터리 내에서 파일을 생성하고, 셸 또는 Python 명령을 실행하고, 출력을 검사할 수 있다. Workspace는 state를 유지하여 반복적인 개발을 가능하게 한다. 에이전트는 데이터 분석, 자동화 또는 동적 코드 생성에 필수적이다. 이를 보완하는 수학 도구는 기본적인 산술 연산을 처리한다.
Experiments
- 모델 구성
- Planner: GPT-4.1
- Executor: o3 / o4-mini
- 이미지 처리: GPT-4o
- 동영상 에이전트: Gemini 2.5 Pro
- 오디오 에이전트: Assembly AI
- 구현 디테일
- CBR에서는 SimCSE로 문장 인코딩
- parametric CBR의 Q-function: 2-layer MLP
- 각 궤적의 마지막 step의 state, action, reward만 메모리에 기록
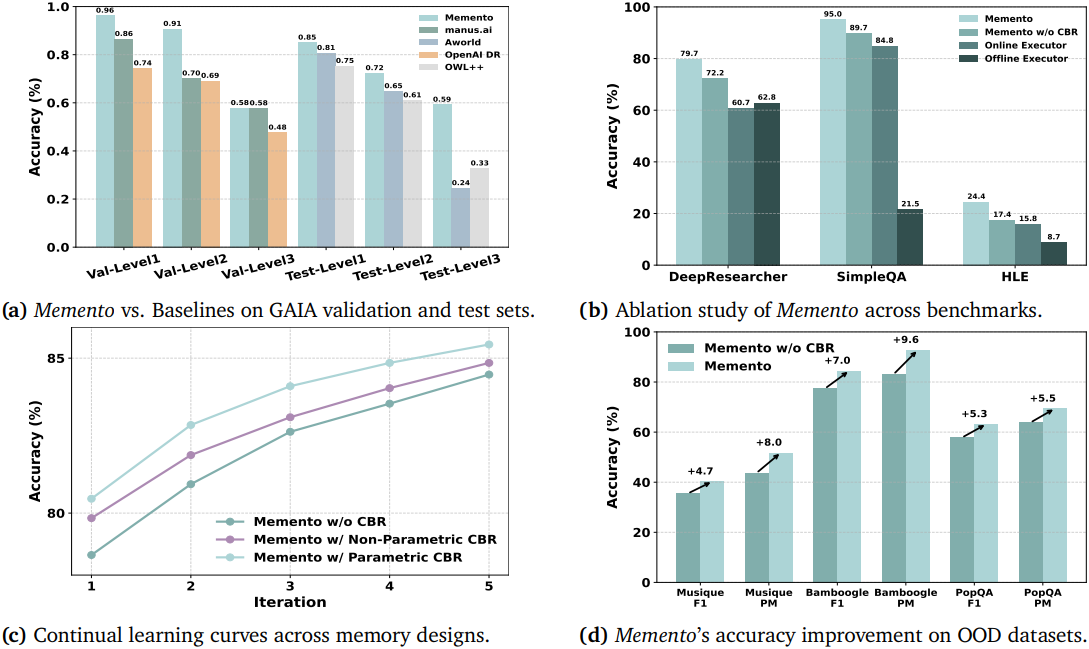
1. Experimental Results
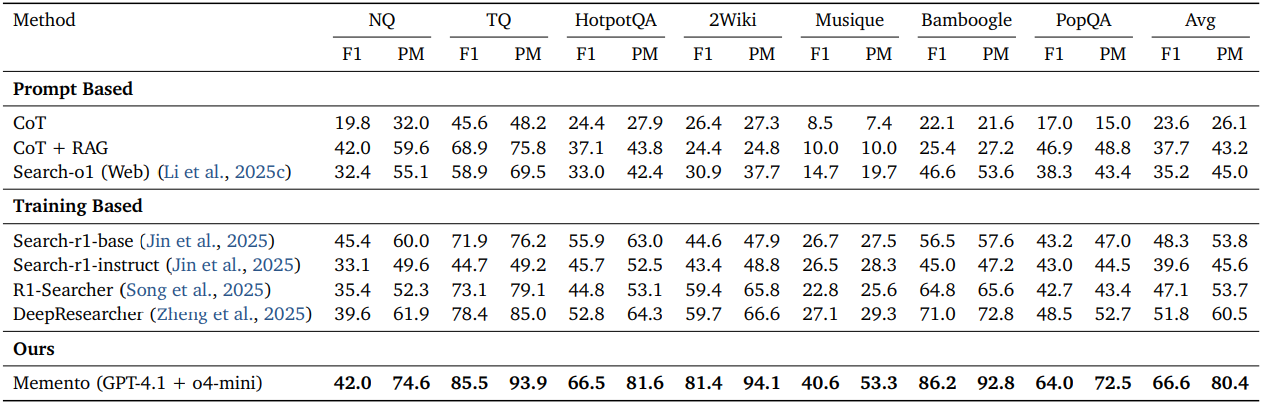
다음은 다양한 open-domain QA 데이터셋에 대한 비교 결과이다.
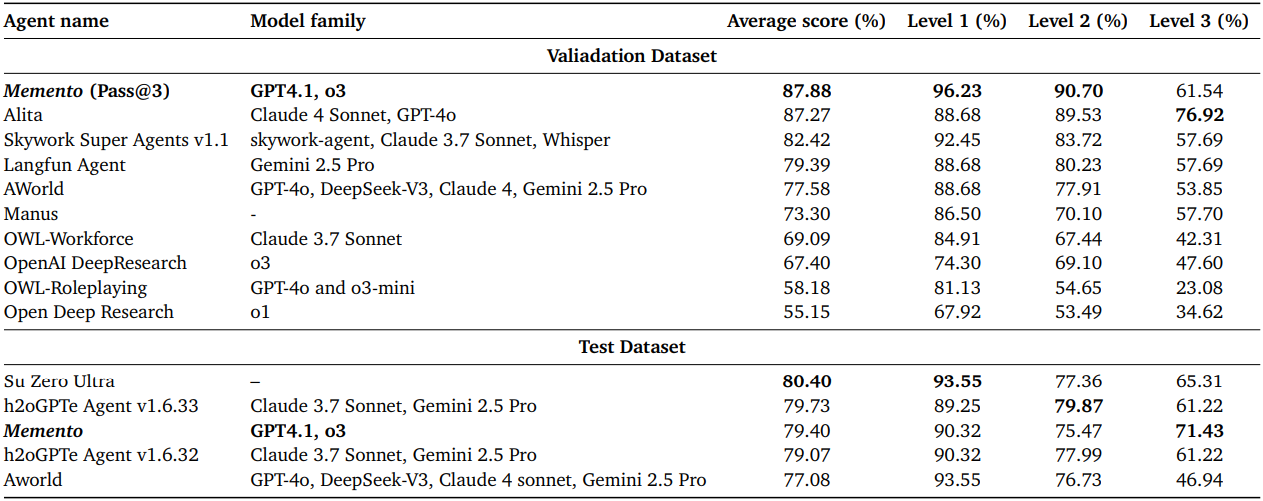
다음은 2025년 6월 26일 기준 GAIA 리더보드의 결과이다.
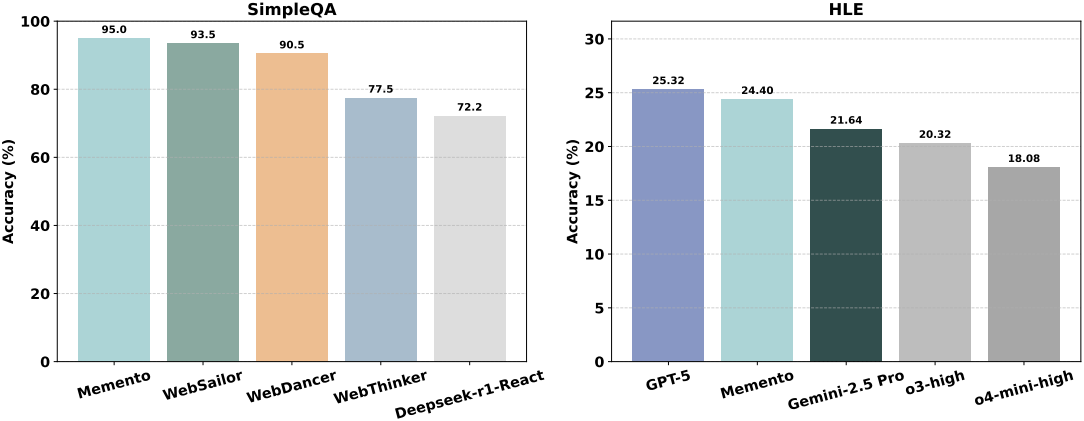
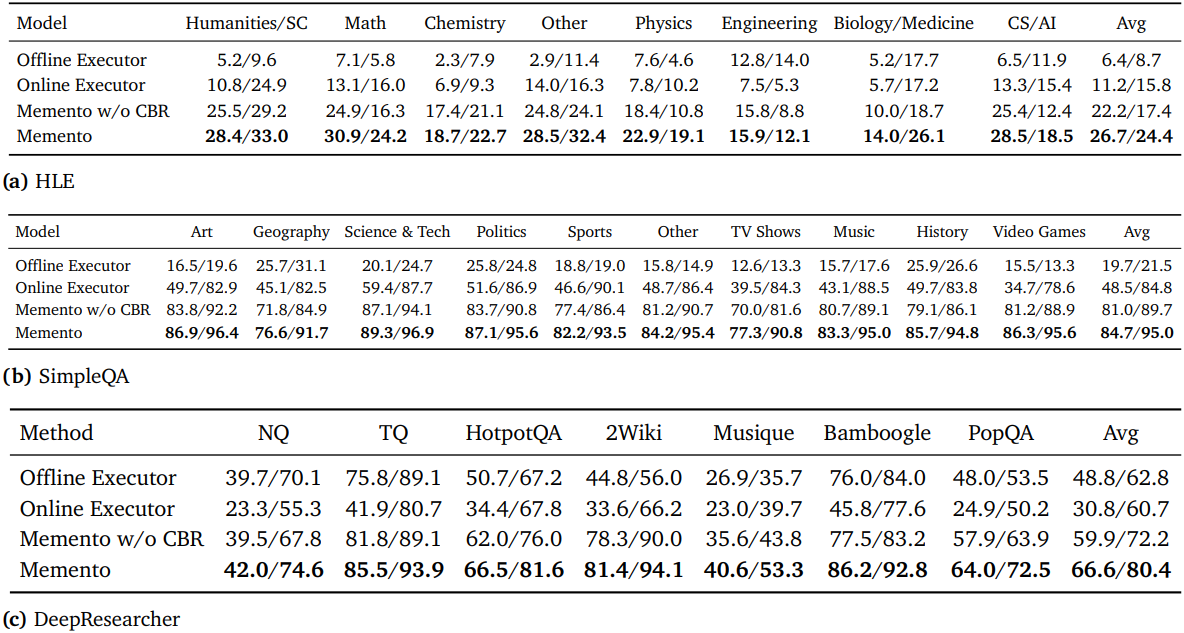
다음은 SimpleQA와 HLE에서의 성능을 비교한 결과이다.
2. Ablation Studies
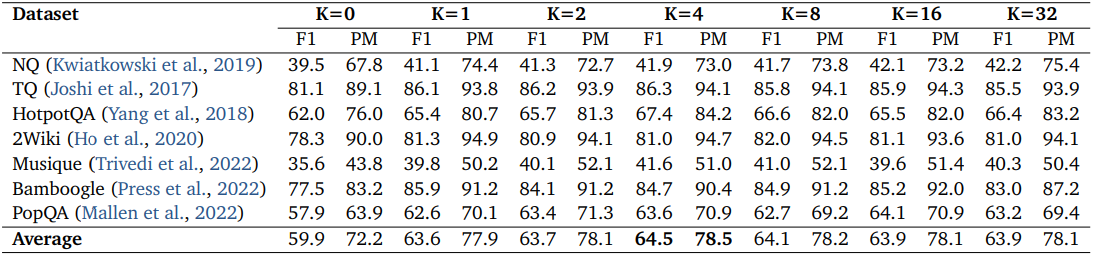
다음은 검색 횟수 $K$에 따른 성능을 비교한 결과이다. (DeepResearcher)
다음은 구성 요소에 대한 ablation study 결과이다.
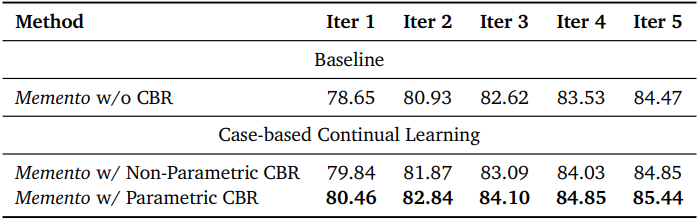
다음은 CBR에 대한 continual learning 성능을 비교한 결과이다.
3. Analysis
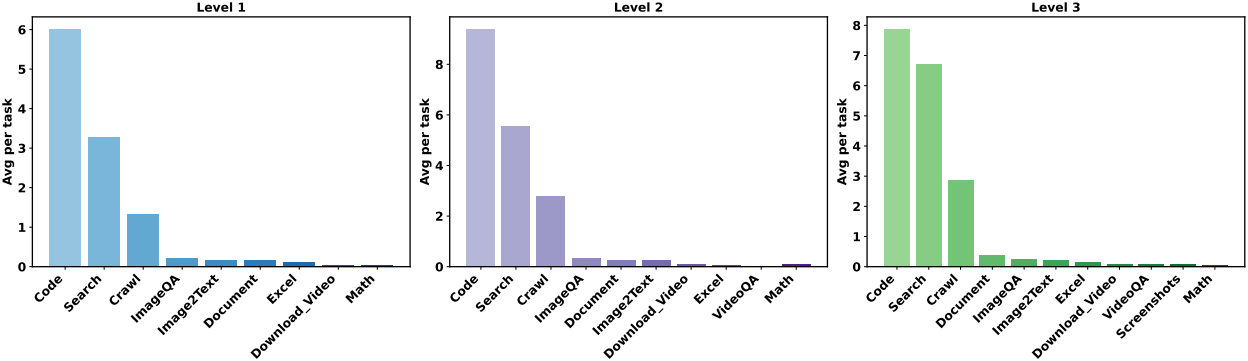
다음은 task 난이도에 따른 각 도구의 평균 사용 횟수를 비교한 그래프이다.
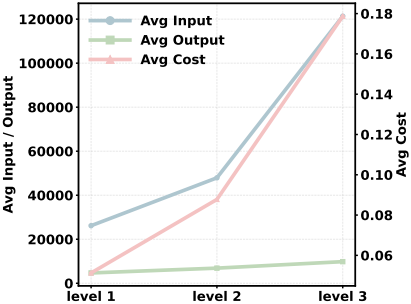
다음은 task 난이도에 따른 토큰 비용을 비교한 그래프이다.
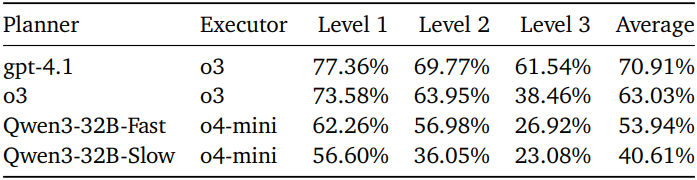
다음은 fast-thinking 모드와 slow-thinking 모드에 대한 영향을 비교한 결과이다.