[논문리뷰] Multi-Architecture Multi-Expert Diffusion Models (MEME)

AAAI 2024. [Paper]
Yunsung Lee, Jin-Young Kim, Hyojun Go, Myeongho Jeong, Shinhyeok Oh, Seungtaek Choi
Riiid AI Research
8 Jun 2023

Introduction

Diffusion model은 생성 모델링을 위한 유망한 접근 방식이며 다양한 도메인에서 점점 더 중요한 역할을 할 가능성이 높다. 그러나 인상적인 성능에도 불구하고 diffusion model은 두 가지 직교 요소에서 비롯된 높은 계산 비용으로 어려움을 겪는다.

1. 길고 반복적인 denoising process
2. 무거운 denoiser network

이러한 한계를 극복하기 위한 여러 노력이 있었지만 이러한 노력의 대부분은 첫 번째 요인을 해결하는 데만 집중되어 있어 무거운 denoiser가 여전히 실제 시나리오에 대한 적용 가능성을 제한한다. 이전 연구들은 몇 가지 노력으로 denoiser의 크기를 줄이지만 일반적으로 정확도를 타협하여 이러한 효율성을 달성한다.

따라서 본 논문에서는 소형이지만 대형 모델과 성능이 비슷한 diffusion model을 구축하는 것을 목표로 한다. 전통적인 diffusion model이 방대한 파라미터를 필요로 하는 이유는 주파수 관점에서 모델이 다양한 timestep에서 너무 많은 다른 feature를 학습해야 하기 때문이다. 여기서 diffusion model은 초기에 저주파 성분 (ex. 전체 이미지 윤곽선)을 형성한 다음 고주파 주파수 성분 (ex. 세부 텍스처)을 채우는 경향이 있다. 그러나 denoiser network를 선형 필터로 가정하여 실용적이지 않으므로 저자들은 이 주장을 뒷받침할 경험적 증거를 조사하는 것을 목표로 한다. 구체적으로, 저자들은 각 timestep $t$에서 입력 $x_t$에 대한 레이어별 푸리에 스펙트럼을 분석하여 $t$가 진행됨에 따라 푸리에 변환된 feature map의 상대적 로그 진폭에 중요하고 일관된 변화가 있음을 발견했다. 이 발견은 대형 모델의 비용이 많이 드는 학습 프로세스가 실제로 각 timestep $t$에서 서로 다른 주파수 특성에 적응하는 학습을 포함한다는 것을 나타낸다.

이 결과를 활용하는 한 가지 방법은 모델이 할당된 timestep 간격에 특화되도록 여러 diffusion model에 고유한 timestep 간격을 할당하는 것이며, multi-expert 전략이라 부른다. 그러나 조건부 생성을 위한 multi-expert 전략을 guidance와 함께 활용하고 고성능에 중점을 두었기 때문에 주파수 관점에서 다른 timestep에서 다른 연산이 더 적합할 수 있다는 사실을 무시하고 효율성을 고려하지 않았다.

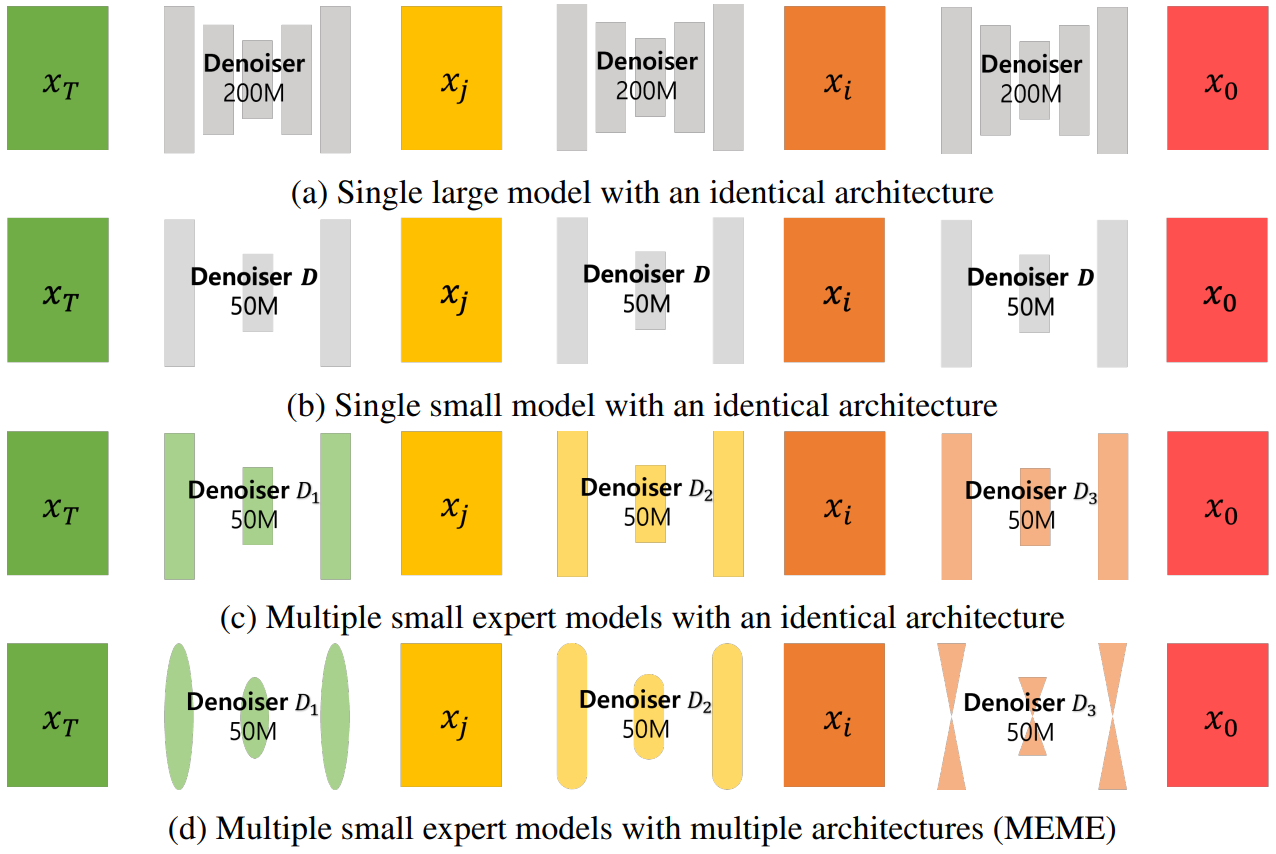
이를 위해 본 논문은 각각의 주파수 범위에 따라 기본 동작이 달라지는 서로 다른 timestep 간격에 대해 서로 다른 아키텍처를 가진 서로 다른 모델을 할당할 것을 제안한다. 이를 Multi-architecturE Multi-Expert diffusion model (MEME)이라고 한다. 구체적으로, 고주파 성분 ($t$ ~ $0$)을 처리하는 데 convolution이 유리하고 저주파 성분 ($t$ ~ $T$)을 처리하는 데 multi-head self-attention (MHSA)이 뛰어나다는 통찰력을 활용한다. 그러나 feature가 본질적으로 고주파 성분과 저주파 성분의 조합이기 때문에 서로 다른 timestep 간격에 두 개의 다른 아키텍처를 단순히 배치하는 것은 최선이 아니다.

본 논문은 이러한 주파수별 성분의 복잡한 분포에 더 잘 적응하기 위해 convolution 연산과 MHSA 연산 사이의 채널별 균형 비율을 조정할 수 있는 iFormer 블록을 통합하는 iU-Net이라는 보다 유연한 denoiser 아키텍처를 제안한다. Denoising process에서 저주파 성분을 먼저 복구하고 점진적으로 고주파 feature를 추가하는 diffusion model의 특성을 활용한다. 결과적으로 각 아키텍처가 다른 비율의 MHSA를 갖도록 구성하여 diffusion process의 다른 timestep 간격에서 고유한 요구 사항에 맞게 각 아키텍처를 효과적으로 조정한다.

저자들은 유연한 iU-Net에 특정 timestep 간격에 효과적으로 집중하는 방법을 추가로 탐색하였다. 구체적으로, 하드한 분할보다 소프트한 분할을 선호하는 multi-expert 모델들에 대한 소프트한 간격 할당 전략을 식별한다. 이 전략은 $T$에 더 가까운 간격에 할당된 expert가 전체 timestep에서 학습할 수 있는 더 많은 기회를 가질 수 있도록 하여 timestep $t$ ~ $T$에서 무의미한 noise에 과도하게 노출되는 것을 방지한다.

Background

1. Diffusion Models and Spectrum Evolution over Time

Diffusion model은 latent 변수를 사용하여 step별 noising process를 reverse하여 작동한다. 실제 분포의 데이터 포인트 $x_0$는 평균이 0인 Gaussian noise와 $T$ step에 걸친 $\beta_t$ 분산에 의해 교란되어 결국 Gaussian white noise에 도달한다. Noise 변경 분포 $q(x_t)$에서 효율적으로 샘플링하는 것은 임의의 timestep $x_t$를 생성하는 closed form 표현식을 통해 가능하다.

\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, \\ \textrm{where} \quad \epsilon \sim \mathcal{N}(0, I), \; \alpha_t = 1 - \beta_t, \; \bar{\alpha}_t = \prod_{s=1}^t \alpha_s \end{equation}\]

시간으로 컨디셔닝된 denoising 신경망인 denoiser $s_\theta (x, t)$는 다음과 같이 noise에 적응하여 ELBO를 최소화하여 diffusion process를 반전시키도록 학습된다.

\[\begin{equation} \mathbb{E}_{t, x_0, \epsilon} [\| \nabla_{x_t} \log p (x_t \vert x_0) - s_\theta (x_t, t) \|_2^2] \end{equation}\]

본질적으로 denoiser는 데이터 log-likelihood를 최적화하는 기울기를 복구하는 방법을 학습한다. 학습된 denoiser를 활용하여 Markov chain을 반전시켜 이전 step 데이터 $x_{t-1}$을 생성한다.

\[\begin{equation} x_{t-1} \leftarrow \frac{1}{\sqrt{1 - \beta_t}} (x_t + \beta_t s_\theta (x_t, t)) + \sqrt{\beta_t} \epsilon_t \end{equation}\]

이 reverse process에서 diffusion model은 coarse model에서 fine model로 진화한다. 네트워크를 선형 필터로 간주하면 주파수 관점에서 수치적 설명이 가능하다. 이 경우 Wiener filter로 알려진 최적의 필터는 모든 timestep에서 스펙트럼 응답으로 표현될 수 있다. $x_0$의 파워 스펙트럼

\[\begin{equation} \mathbb{E} [\|X_0 (f) \|^2] = \frac{A_s (\theta)}{f^{\alpha_S (\theta)}} \end{equation}\]

가 power law를 따른다는 가정 하에서 신호 재구성 필터의 주파수 응답은 진폭 scaling factor $A_s (\theta)$와 주파수 지수 $\alpha_S (\theta)$로 결정된다. Reverse process가 $t = T$에서 $t = 0$으로 진행되고 $\alpha$가 0에서 1로 증가함에 따라 diffusion model은 시간이 지남에 따라 스펙트럼 변화 동작을 나타낸다. 초기에 narrow-banded filter는 대략적인 구조를 담당하는 저주파 성분만 복원한다. $t$가 감소하고 $\bar{\alpha}$가 증가함에 따라 사람의 머리카락, 주름, 모공과 같은 더 많은 고주파 성분이 이미지에서 점차 복원된다.

2. Inception Transformer

컴퓨터 비전에서 trasnformer의 한계는 글로벌 정보를 전달하는 저주파 feature를 캡처하는 경향이 있지만 로컬 정보에 해당하는 고주파 feature를 캡처하는 데 능숙하지 않다는 것이다. 이러한 단점을 보완하기 위해 Inception 모듈을 활용하여 convolution layer와 transformer를 결합한 Inception Transformer가 도입되었다.

입력 feature $Z \in \mathbb{R}^{N \times d}$는 먼저 채널 차원을 따라 $Z_h \in \mathbb{R}^{n \times d_h}$와 $Z_l \in \mathbb{R}^{n \times d_l}$로 분리된다. 여기서 $d = d_h + d_l$이다. 그런 다음 iFormer 블록은 $Z_h$에 고주파 믹서를 적용하고 $Z_l$에 저주파 믹서를 적용한다. 구체적으로 $Z_h$는 다음과 같이 채널 차원을 따라 $Z_{h1}$과 $Z_{h2}$로 더 분할된다.

\[\begin{equation} Y_{h1} = \textrm{FC} (\textrm{MP} (Z_{h1})) \\ Y_{h2} = \textrm{D-Conv} (\textrm{FC} (Z_{h2})) \end{equation}\]

여기서 $Y$는 고주파 믹서의 출력, $\textrm{FC}$는 fully-connected layer, $\textrm{MP}$는 max pooling layer, $\textrm{D-Conv}$는 depth-wise convolutional layer를 나타낸다.

저주파 믹서에서 MHSA는 포괄적이고 응집력 있는 표현을 얻기 위해 활용된다. 이 글로벌 표현은 고주파수 믹서의 출력과 결합된다. 그러나 업샘플링 연산의 잠재적인 오버스무딩 효과로 인해 이 문제를 해결하고 최종 출력을 생성하기 위해 퓨전 모듈이 도입되었다.

\[\begin{equation} Y_l = \textrm{Up} (\textrm{MHSA} (\textrm{AP} (Z_{h2}))) \\ Y_c = \textrm{Concat} (Y_{h1}, Y_{h2}, Y_l) \\ Y = \textrm{FC} (Y_c + \textrm{D-Conv} (Y_c)) \end{equation}\]

여기서 $\textrm{Up}$은 업샘플링, $\textrm{AP}$는 average pooling, $\textrm{Concat}$은 concatenation을 나타낸다.

Frequency Analysis for Diffusion Models

블록의 깊이에 따라 적절한 주파수를 캡처하는 별개의 블록으로 아키텍처를 설계하는 것이 유용하다. 따라서 저자들은 시간에 따른 모델별 latent와 추출 feature의 주파수 기반 특성을 분석하였다.

1. Frequency Component from Latents

가우시안 필터가 고주파에서 필터링을 우선시한다는 사실로부터 diffusion model에 공급된 학습 데이터가 $t$가 증가함에 따라 점차적으로 고주파 스펙트럼을 잃는다는 것이 분명하다.

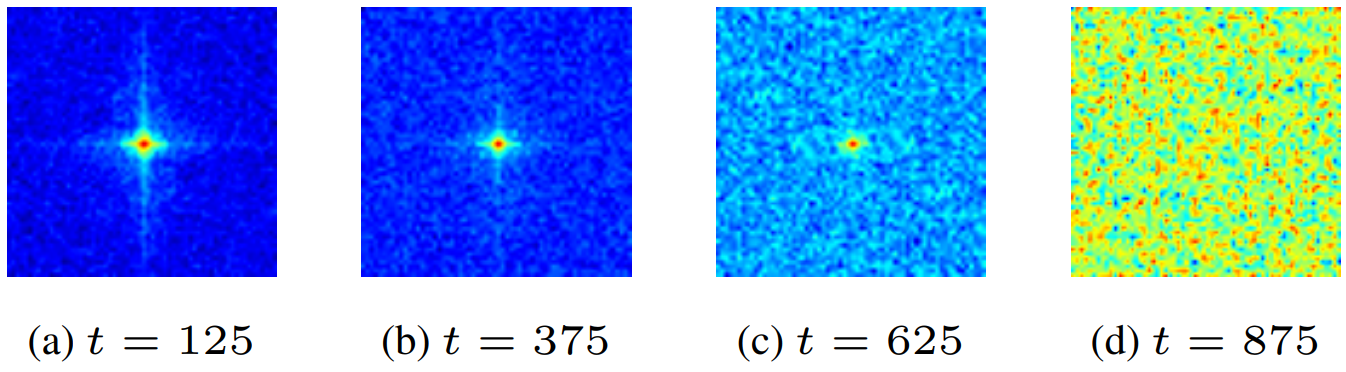
위 그림은 해당 주파수에 대한 주기 함수의 푸리에 계수를 보여줌으로써 학습 데이터가 $t$가 증가함에 따라 점차적으로 고주파 스펙트럼을 잃는다는 것을 보여준다. 따라서 해당 feature를 처리하기 위한 timestep에 따라 서로 다른 주파수 성분을 필터링하는 diffusion model을 설계해야 함이 분명하다.

2. Frequency Component Focused by Model

다음은 사전 학습된 latent diffusion model (LDM)에서 얻은 푸리에 변환된 feature map의 상대적인 로그 진폭을 비교한 그래프이다.

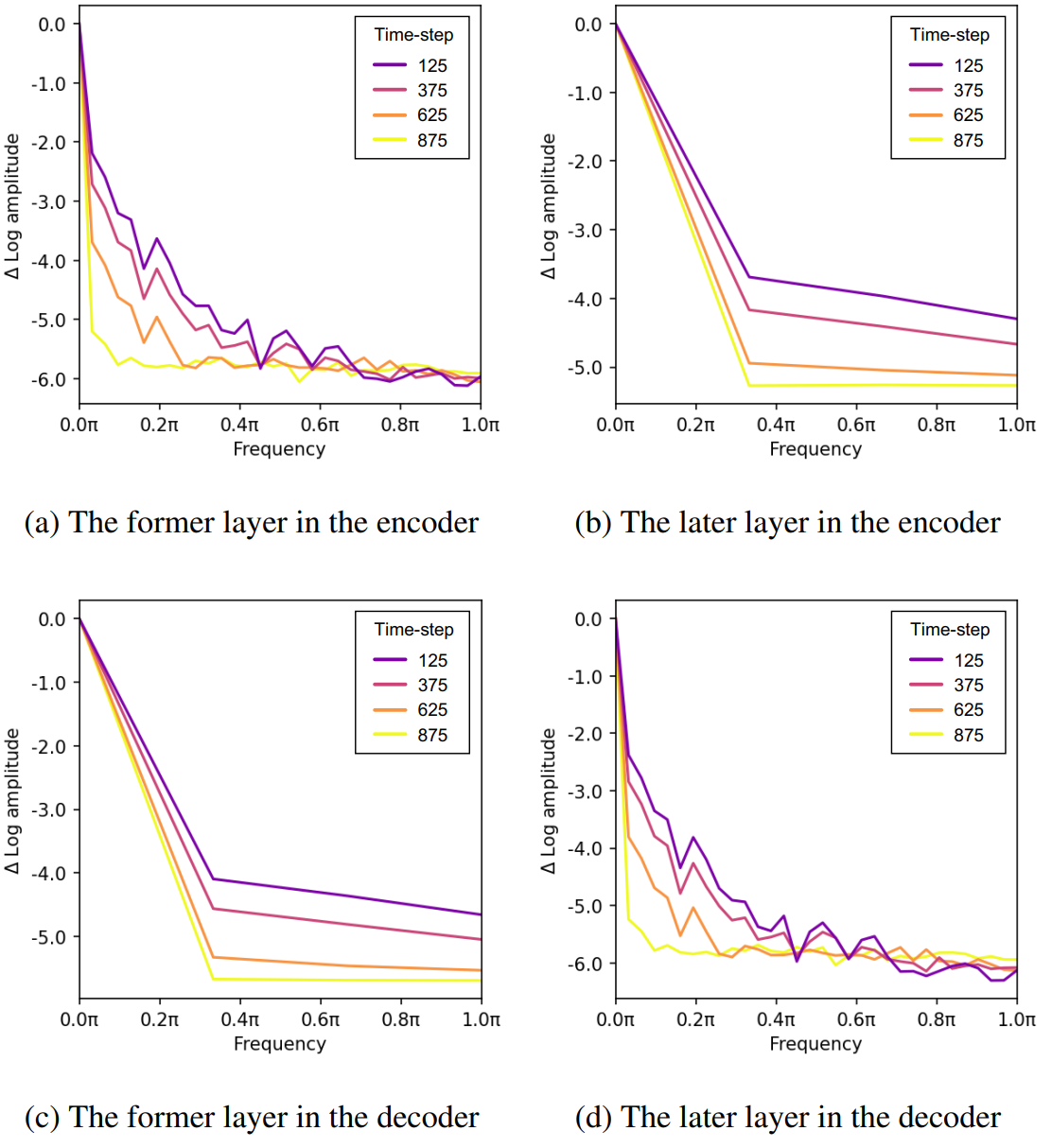
위 그림에서 볼 수 있듯이 이미지 인식 신경망은 주로 이전 레이어에서 high-pass filtering을 수행하고 이후 레이어에서 low-pass filtering을 수행함을 보여준다. 또한 diffusion model은 $t$가 증가함에 따라 저주파 신호를 더 현저하게 감쇠시키는 경향이 있다. 이러한 발견은 주로 고주파 성분을 억제하는 경향으로 알려진 가우시안 필터의 잘 확립된 특성과 일치한다.

Multi-Architecture Multi-Expert Diffusion Models

위의 관찰을 바탕으로 저자들은 다음과 같은 중요한 가설을 제안하였다.

각 timestep에 따라 달라지는 연산으로 denoising model을 구성함으로써 잠재적으로 diffusion model의 학습 프로세스의 효율성을 향상시킬 수 있다.

이 가설을 검증하려면 두 가지 핵심 요소가 필요하다.

1. 높은 주파수 또는 낮은 주파수에 대한 전문화 정도를 조정할 수 있는 denoiser 아키텍처
2. Diffusion process 전반에 걸쳐 이 맞춤형 아키텍처의 적용을 다양화하기 위한 전략

1. iU-Net Architecture

본 논문은 고주파와 저주파에 유리한 동작 비율을 조정할 수 있는 U-Net의 변형인 iU-Net 아키텍처를 제안하였다. High-pass filtering에 적합한 convolution 연산과 low-pass filtering에 적합한 Multi-Head Self-Attention (MHSA) 연산을 inception mixer와 엮는 inception transformer (iFormer)라는 블록을 활용한다.

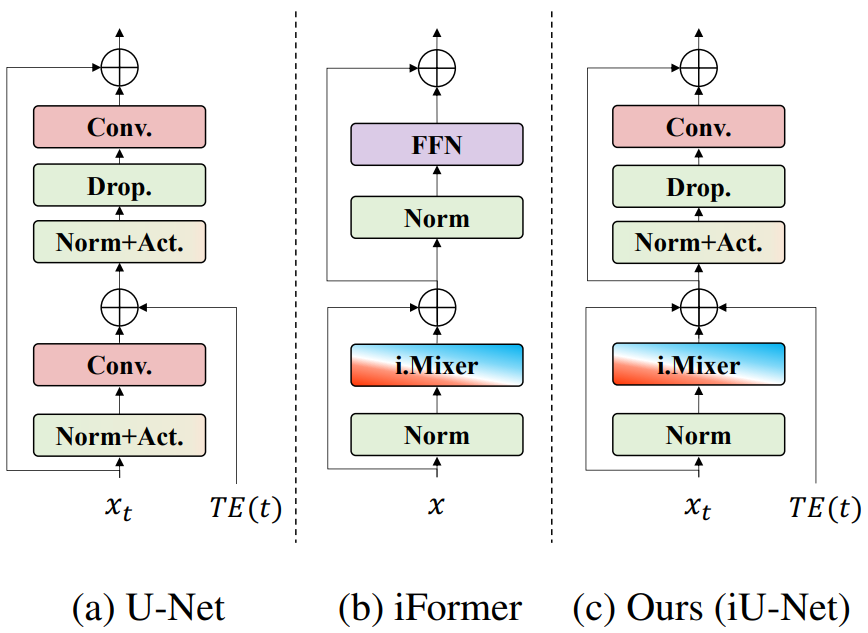
위 그림은 denoiser diffusion 아키텍처에 맞게 iFormer 블록을 조정한 방식을 보여준다. 이 설정을 통해 iFormer 블록은 아키텍처 구성에서 convolution-heavy 고주파 믹서와 MHSA-heavy 저주파 믹서 사이의 비율을 조절할 수 있다. Convolution과 MHSA를 결합하려고 시도한 후, 이후 레이어에서 더 많은 MHSA 연산을 수행하도록 iU-Net 인코더를 설정한다. 또한 U-Net 블록에서 iFormer 블록으로 블록 아키텍처를 완전히 대체하는 것보다 두 가지를 비대칭적으로 병합하는 것이 iFormer를 활용한 diffusion model을 위한 아키텍처를 구성하는 데 효과적이다.

2. Multi-Architecture Multi-Expert Strategy

Architecture Design for Experts

다양한 아키텍처를 수용할 수 있는 구조의 구축을 용이하게 하기 위해 multi-expert 전략을 사용하지만 주파수 성분에 따라 각 expert에게 서로 다른 아키텍처를 할당한다. 각 아키텍처에서 높은 채널과 낮은 채널의 차원 크기 비율은 레이어 깊이와 timestep이라는 두 가지 요소로 정의된다.

전자는 더 깊은 레이어로 더 낮은 주파수에 집중하여 주파수 동적 feature 추출을 가능하게 하는 것으로 잘 알려져 있다. $d^k$를 $k$번째 레이어의 채널 크기, $d_h^k$를 high mixer의 차원 크기, $d_l^k$로 low mixer의 차원 크기라고 하고 $d^k = d_h^k + d_l^k$을 만족한다. 각 iFormer 블록의 비율은 깊이에 따라 적절한 주파수 성분을 처리하기 위해 정의된다. $d_h^k / d_l^k$는 블록이 깊어질수록 감소한다.

반면에 timestep은 주파수 성분과 연관될 수 있다. Timestep $t$가 증가함에 따라 더 낮은 주파수 성분이 집중된다. 따라서 더 큰 $t$에서 denoiser가 전문가를 담당하는 경우 $d_h^k / d_l^k$의 비율이 더 빨리 감소하도록 iU-Net 아키텍처를 구성한다.

Soft Expert Strategy

$N$개의 expert 중 하나인 $\Theta_n$는 $n = 1, \cdots, N$에 대해 균일하고 분리된 간격

\[\begin{equation} \mathbb{I}_n = \bigg\{ t \vert t \in \bigg( \frac{n-1}{N} T, \frac{n}{N} T \bigg] \bigg\} \end{equation}\]

에 대해 학습을 받는다. 그러나 큰 $n$의 경우 $\Theta_n$은 Gaussian noise

\[\begin{equation} \epsilon_n \sim \mathcal{N} (\sqrt{\vphantom{1} \bar{\alpha}_n} x_0, (1 - \bar{\alpha}_n) I ) \end{equation}\]

에 가까운 noisy한 입력 이미지를 취하므로 $\Theta_n$으로 의미 있는 학습이 이루어지기 어렵다. 이 문제를 해결하기 위해 각 $\Theta_n$이 전문화 확률로 표시되는 $p_n$의 확률로 간격 \(\mathbb{I}_n\)에서 학습하는 soft expert strategy을 제안한다. 그렇지 않으면 나머지 $(1 - p_n)$의 확률로 전체 간격 \(\bigcup_{n=1}^N \mathbb{I}_n\)에서 학습한다.

큰 $n$에 대한 $\Theta_n$이 더 많은 noise가 있는 이미지를 취한다는 것이 명백하기 때문에 $n$이 $N$으로 갈수록 더 큰 $p_n$을 가지는 것이 multi-expert 학습을 위한 보다 유연한 전략이다.

Experiments

1. Image Generation Results

다음은 FFHQ와 CelebA-HQ에서의 unconditional한 생성 결과이다.

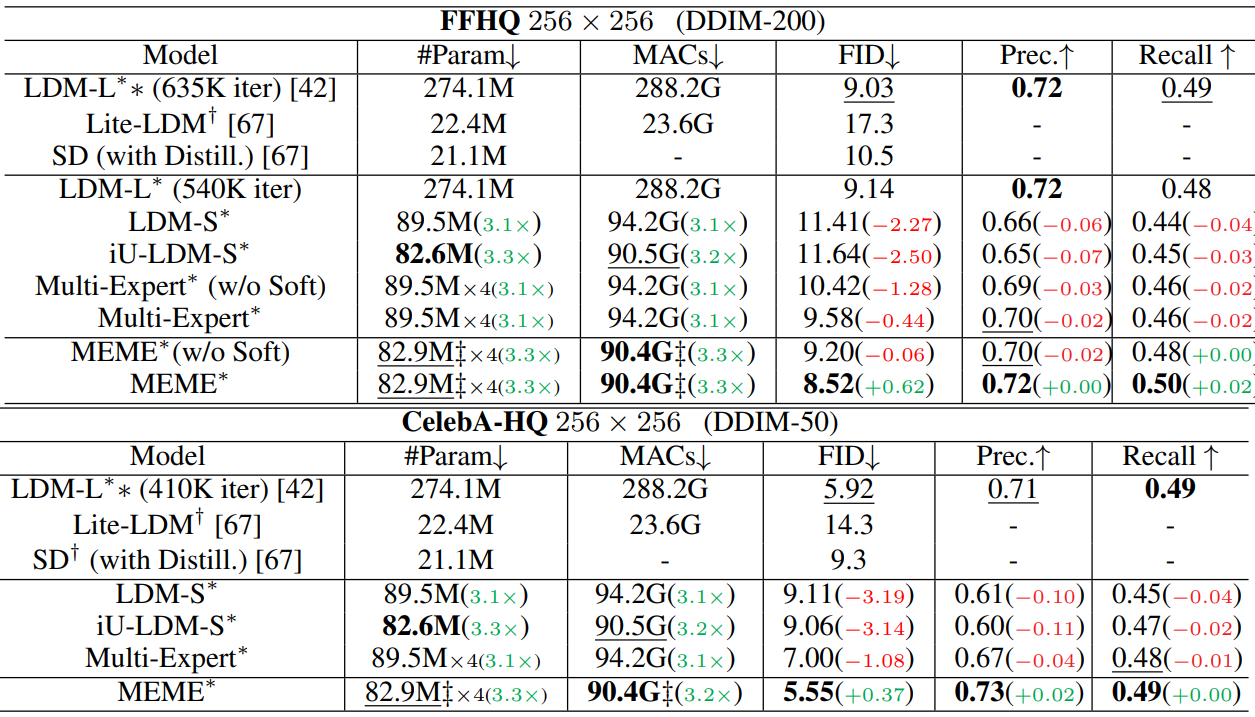
다음은 FFHQ에서 학습된 LDM-L과 MEME의 샘플들을 비교한 것이다.

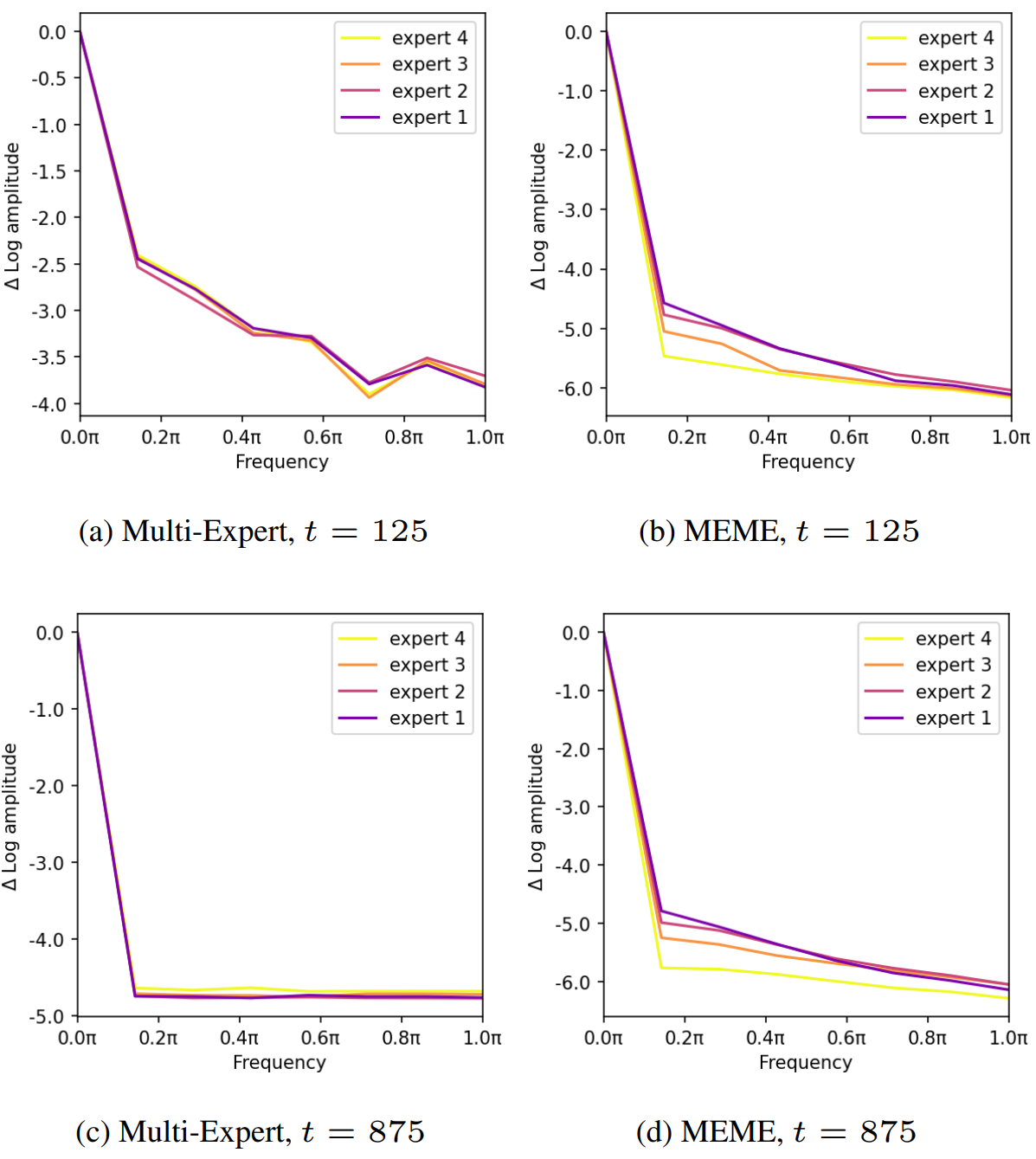
2. Fourier Analysis of MEME

다음은 multi-expert와 MEME의 푸리에 분석 결과를 비교한 그래프이다.

3. MEME on Top of the Other Diffusion Baseline

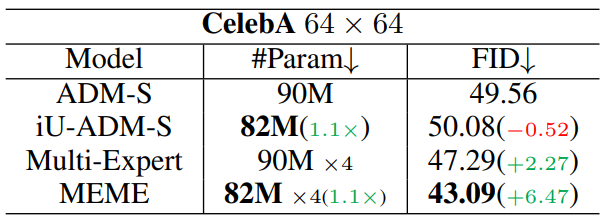
다음은 ADM baseline에 적용한 결과이다.