[논문리뷰] Multi-view Self-supervised Disentanglement for General Image Denoising (MeD)

ICCV 2023. [Paper] [Page] [Github]
Hao Chen, Chenyuan Qu, Yu Zhang, Chen Chen, Jianbo Jiao
University of Birmingham | Shanghai Jiao Tong University | University of Central Florida
10 Sep 2023

Introduction

이미지 복원은 컴퓨터 비전의 중요한 분야로, 손상된 관찰로부터 이미지 신호를 재구성하는 방법을 탐구한다. 이러한 잘못된 저수준 이미지 복원 문제의 예로는 image denoising, super-resolution, JPEG 아티팩트 제거 등이 있다. 일반적으로 문제를 해결하기 위해 손상된 이미지와 깨끗한 이미지 사이에서 학습 데이터 분포를 위한 매핑 함수를 학습시킨다. 많은 이미지 복원 시스템은 지금까지 본 것과 동일한 손상 분포를 통해 평가할 때 좋은 성능을 발휘하지만 환경을 알 수 없거나 학습 분포에서 벗어난 설정에 배포해야 하는 경우가 많다. 또한 현실의 많은 image denoising task에서는 ground-truth 이미지를 사용할 수 없으므로 추가적인 문제가 발생한다.

기존 방법들의 한계점: 현재 낮은 수준의 손상 제거 task는 “주어진 손상된 관찰에 대한 깨끗한 이미지는 무엇인가?”라는 질문을 해결하는 것을 목표로 한다. 그러나 이 문제 구성의 잘못된 성격은 고유한 해결 방법을 얻는 데 상당한 어려움을 초래한다. 이러한 제한을 완화하기 위해 종종 명시적 또는 암시적으로 추가 정보를 도입한다. 예를 들어 noise에 대한 사전 지식을 보완 입력으로 명시적으로 사용하거나 feature space에서 해석 가능성을 암시적으로 적용한다. 그러나 이러한 추가 형태의 정보는 실제 시나리오에서 항상 실용적이지는 않거나 만족스러운 성능을 제공하지 못할 수 있다.

주요 아이디어 및 문제 구성: 이를 해결하려는 본 논문의 동기는 실제 장면에 대한 고유한 평가를 제공하기 위해 여러 뷰를 활용하는 3D 재구성 솔루션에서 비롯된다. 본 논문은 이러한 동기를 바탕으로 여러 손상된 뷰를 기반으로 명시적으로 구축되고 Multi-view self-supervised Disentanglement (MeD)를 수행하는 학습 계획을 제안한다.

이 새로운 멀티뷰 설정에서 문제를 “이러한 뷰에서 공유되는 latent 정보는 무엇인가까?”로 재구성한다. 이를 통해 MeD는 멀티뷰 데이터의 장면 일관성을 효과적으로 활용하고 깨끗한 이미지에 액세스하지 않고도 기본 공통 부분을 캡처할 수 있다. 이를 통해 실제 시나리오에서 더욱 실용적이고 확장 가능해진다.

구체적으로, 깨끗한 이미지 집합 $\mathcal{X}$에서 균일하게 샘플링된 임의의 장면 이미지 $x^k \sim \mathcal{X}, k \in \mathbb{N}$이 주어지면 MeD는 두 가지 오염된 뷰를 생성한다.

\[\begin{equation} y_1^k = \mathcal{T}_1 (x^k), \quad y_2^k = \mathcal{T}_2 (x^k) \end{equation}\]

이를 통해 두 개의 독립적인 손상된 이미지 집합 \(\{\mathcal{Y}_1\}\), \(\{\mathcal{Y}_2\}\)를 형성한다. 여기서 \(y_1^k \in \mathcal{Y}_1\), \(y_2^k \in \mathcal{Y}_2\)이다. \(\mathcal{T}_1\)과 \(\mathcal{T}_2\)는 두 개의 랜덤한 독립적인 이미지 degradation task를 나타낸다. 장면 feature 인코더 $G_\theta^\mathcal{X}$와 디코더 $D_\psi^\mathcal{X}$를 $\theta$와 $\psi$로 parameterize한다. 이미지 쌍 \(\{y_1^k, y_2^k\}_{k \in \mathbb{N}}\)을 고려하면 제시된 방법의 핵심은 다음과 같이 요약될 수 있다.

\[\begin{equation} G_\theta^\mathcal{X} (y_1^k) = z_x^{k,i} = G_\theta^\mathcal{X} (y_2^k) \\ \hat{x}^k = D_\psi^\mathcal{X} (z_x^{k,i}) \end{equation}\]

여기서 $z_x^{k,i}$는 $y_1^k$와 $y_2^k$ 사이에 공유된 장면 latent를 나타내며, $i$는 $y_i$의 입력 이미지 인덱스를 참조한다. $D_\psi^\mathcal{X}$는 $z_x^{k,i}$로부터 전체 역 매핑을 형성하여 깨끗한 이미지 $\hat{x}^k$를 재구성한다.

마찬가지로, noise latent $u_\eta^{k,i}$는 손상 인코더 $E_\rho^N$를 사용하여 손상된 뷰에서 분리된다. 그 후, 손상은 $F_\phi^N$로 표시되는 손상 디코더를 사용하여 $u_\eta^{k,i}$로부터 재구성된다.

그런 다음 파라미터 $\delta$를 사용하는 교차 합성 디코더 $R_\delta^\mathcal{Y}$에 의해 \(\{z_x^{k,i}, u_\eta^{k,j}\}_{i \ne j}\) 사이에서 disentanglement가 수행되며, 이는 다음과 같이 쓸 수 있다.

\[\begin{equation} \hat{y}_1^k = R_\delta^\mathcal{Y} (z_x^{k,2}, u_\eta^{k,1}) \end{equation}\]

위 식은 서로 다른 뷰에서 latent feature $u$와 $z$에 대해 수행된다. $z_x^k$가 뷰 전체에서 일정하게 유지된다고 가정할 때 재구성된 뷰 \(\hat{y}_1^k\)는 $u_\eta^{k,1}$에 의해 결정된다.

Methodology

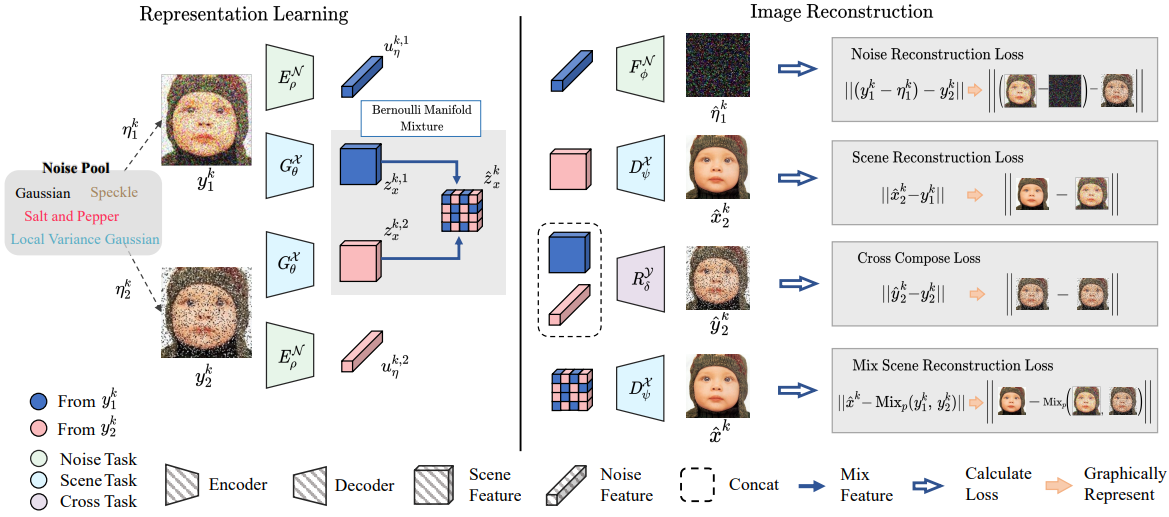
본 논문의 주요 목표는 denoising process에서 다양한 뷰 간의 공통점을 식별하는 것이다. 이를 위해 Multi-view self-supervised Disentanglement (MeD)를 통해 다양한 손상된 뷰 \(\{y_i^k\}_{k \in \mathbb{N}}\)에 대해 degradation에 무관한 공유 장면 $z_x^k$를 발견하는 것을 목표로 한다. MeD의 그래픽 묘사는 위 그림과 같다.

미리 가정된 속성들

장면 latent space와 손상 latent space가 각각 \(\mathcal{Z}_x\)와 \(\mathcal{U}_\eta\)라 가정하자.

1. Independence: 모든 장면 latent \(z_x^k \in \mathcal{Z}_x\)에 대해 모든 손상 latent \(u_\eta^{k,i} \in \mathcal{U}_\eta\)와 무관할 것으로 예상된다.
2. Consistency: 집합 \(\{y_i^k\}\)에 있는 모든 인스턴스의 공유된 꺠끗한 성분을 나타낼 수 있는 하나의 공유 latent code \(z_x^k \in \mathcal{Z}_x\)가 존재한다.
3. Composability: 손상된 뷰 $y_i^k$의 복구는 feature 쌍 $z_x^k$, $u_\eta^{k,i}$를 사용하여 달성할 수 있으며, 복구된 뷰의 인덱스는 해당 특정 뷰 내의 고유 성분을 나타내는 손상 latent의 인덱스에 의해 결정된다.

본 논문의 핵심 단계는 latent space 가정을 구현하는 방법을 결정하여 이러한 전제 조건들을 실현하는 것이다. Latent space 가정을 추론하기 위해 MeD는 두 개의 인코더와 세 개의 디코더로 구성된다.

• 공유 콘텐츠 latent 인코더 $G_\theta^\mathcal{X}$ 및 디코더 $D_\psi^\mathcal{X}$
• 보조 noise latent 인코더 $E_\rho^\mathcal{N}$ 및 디코더 $F_\phi^\mathcal{N}$
• cross disentanglement 디코더 $R_\delta^\mathcal{Y}$

1. Main Forward Process

동일한 이미지 $x^k$의 두 개의 손상된 뷰 \(y_1^k = \mathcal{T}_1 (x^k)\)와 \(y_2^k = \mathcal{T}_2 (x^k)\)가 주어지면 인코더 $G_\theta^\mathcal{X}$는 주로 다음과 같이 장면 feature space 인코딩을 수행한다.

\[\begin{equation} z_x^{k,1} = G_\theta^\mathcal{X} (y_1^k), \quad z_x^{k,2} = G_\theta^\mathcal{X} (y_2^k) \end{equation}\]

여기서 $z_x^{k,1}$과 $z_x^{k,2}$는 각각 입력 $y_1^k$와 $y_2^k$에 대한 장면 feature의 추정치이다.

깨끗한 이미지 재구성 프로세스는 $D_\psi^\mathcal{X}$에 의해 완료된다.

\[\begin{equation} \hat{x}_1^k = D_\psi^\mathcal{X} (z_x^{k,1}), \quad \hat{x}_2^k = D_\psi^\mathcal{X} (z_x^{k,2}) \end{equation}\]

장면 feature를 추정하는 과정과 유사하게 $E_\rho^\mathcal{N}$으로 왜곡 feature를 추정한 후 $F_\phi^\mathcal{N}$으로 noise를 재구성하는 과정은 다음과 같다.

\[\begin{equation} u_\eta^{k,1} = E_\rho^\mathcal{N} (y_1^k), \quad u_\eta^{k,2} = E_\rho^\mathcal{N} (y_2^k) \\ \hat{\eta}_1^k = F_\phi^\mathcal{N} (u_\eta^{k,1}), \quad \hat{\eta}_2^k = F_\phi^\mathcal{N} (u_\eta^{k,2}) \end{equation}\]

Noisy한 이미지를 supervision 신호로 사용하기 위해 N2N에서 도입한 방법론을 사용한다. 앞서 언급한 프로세스의 목적 함수는 다음과 같이 단순화될 수 있다.

\[\begin{aligned} \underset{\theta, \psi}{\arg \min} \mathcal{L}^\mathcal{X} &= \| \hat{x}_1^k - y_2^k \| \\ \underset{\rho, \phi}{\arg \min} \mathcal{L}^\mathcal{N} &= \| (y_1^k - \hat{\eta}_1^k) - y_2^k \| \end{aligned}\]

\(\hat{x}_2^k\)와 $\hat{\eta}_2^k$의 목적 함수는 첨자만 다를 뿐 위 식과 동일하다. 본 논문의 목적 함수는 N2N의 목적 함수와 유사하지만 본 논문의 목표는 단순히 noise를 찾아 제거하는 것이 아니라 여러 뷰에서 공유되는 공통 feature를 캡처하는 것이다.

2. Cross Disentanglement

일반적인 latent code $z_x^k$가 이미지 공간에서 장면 정보를 충분히 표현하기 위해서는 이러한 code가 어느 정도 자유도를 나타내어 noise space와 교차할 수 있다고 가정하는 것이 당연하다. 결과적으로, $z_x^k$와 $u_\eta^k$ 사이의 완전한 분리가 보장되지 않는다. 속성 (1)과 (3)의 요구 사항을 충족하기 위해 추가 디코더 $R_\delta^\mathcal{Y}$를 사용하여 cross-feature 조합에 대해 손상된 뷰를 재구성한다. 예를 들어, $y_1$의 $z_x^{k,1}$와 $x_2$의 $u_\eta^{k,2}$은 다음과 같이 나타낼 수 있다.

\[\begin{equation} \hat{y}_1^k = R_\delta^\mathcal{Y} (z_x^{k,2}, u_\eta^{k,1}), \quad \hat{y}_2^k = R_\delta^\mathcal{Y} (z_x^{k,1}, u_\eta^{k,2}) \end{equation}\]

이를 실현하려면 $z_x^{k,i}$가 공통 부분을 나타내고 $u_\eta^{k,j}$이 손상된 뷰 내의 고유 부분을 나타내야 한다. 그런 다음 다음과 같은 목적 함수를 사용하여 \(\{\theta, \rho, \delta\}\)를 최적화한다.

\[\begin{equation} \underset{\theta, \rho, \delta}{\arg \min} \mathcal{L}^\mathcal{C} = \| \hat{y}_1^k - y_1^k \| + \| \hat{y}_2^k - y_2^k \| \end{equation}\]

일반적으로, $u_\eta^{k,i}$에 대한 자명한 해 $y_i^k$가 있을 수 있다. 그러나 noise를 재구성하기 위해 $u_\eta^{k,1}$이 명시적으로 필요하며, 이는 $y_1^k$를 표현할 때 $u_\eta^{k,1}$이 붕괴되는 것을 방지한다.

3. Bernoulli Manifold Mixture

앞서 언급한 latent 제약은 처음에는 제한적인 것처럼 보일 수 있지만 실제로는 latent space 구현에서 많은 자유도를 포착할 수 있다. 예를 들어, 단일 장면에 해당하는 여러 장면 feature를 가질 수 있다. 그러나 이러한 경우 입력에서 장면 feature로의 매핑이 모호해진다. 이 문제를 해결하기 위해 본 논문은 장면 latent 내에서 공유 구조를 활용하는 수단으로 Bernoulli Manifold Mixture (BMM)의 사용을 제안한다.

속성 (2)의 가정이 주어지면 획득된 장면 feature $z_x^{k,1}$과 $z_x^{k,2}$는 둘 다 동일한 장면 feature를 참조하므로 서로 동일하고 상호 교환이 가능할 것으로 예상된다. BMM은 여러 뷰의 장면 feature 사이에 새로운 명시적 연결을 설정하며 이는 방정식으로 다음과 같이 표현될 수 있다.

\[\begin{equation} \hat{z}_x^k = \textrm{Mix}_p (z_x^{k,1}, z_x^{k,2}) \end{equation}\]

여기서 \(\hat{z}_x^k\)는 실제 장면 feature의 추정치이다. $b_f$를 베르누이 분포에서 확률 $p \in (0, 1)$로 추출된 샘플 인스턴스라 정의하면 위의 \(\textrm{Mix}_p (\cdot)\) 함수는 다음과 같다.

\[\begin{equation} \textrm{Mix}_p (m, n) = b_f \odot m + (1 - b_f) \odot n \end{equation}\]

이 새로운 연결을 설정함으로써 \(\hat{z}_x^k\)에 대한 재구성 성능을 최적화함으로써 $z_x^{k,1}$과 $z_x^{k,2}$ 사이의 상호 교환성을 향상시킬 수 있다.

---

Lemma 1. \(z_x^{k,i} \sim \mathcal{N}_x (\mu, \Sigma)\)라고 가정하자. 여기서 \(\mathcal{N}_x\)는 다변량 가우스 분포를 나타내고 $\mu$와 $\Sigma$는 평균 및 공분산 행렬이다. 주어진 함수 $G_\theta^\mathcal{X} (\cdot)$에 대해 $\forall k, i, m, n \in \mathbb{N}$을 가정하면 다음 속성이 유지된다.

\[\begin{equation} \mathbb{E} [G_\theta^\mathcal{X} (z_x^{k,i})] = \mathbb{E} [G_\theta^\mathcal{X} (\textrm{Mix}_p (z_x^{k,m}, z_x^{k,n}))] \end{equation}\]

Proof. \(z_x^{k,i}, z_x^{k,n} \in \mathbb{R}^\textrm{dim}\)이 독립항등분포(i.i.d.)라 하자.

\[\begin{equation} \hat{z}_x^k = \mathrm{Mix}_p (z_x^{k,m}, z_x^{k,n}) \end{equation}\]

이라 하면 $b_f^2 = b_f$이기 떄문에

\[\begin{aligned} \hat{z}_x &\sim \mathcal{N}_x ((b_f + 1 - b_f) \mu, (b_f^2 + (1 - b_f)^2) \Sigma) \\ &\sim \mathcal{N}_x ((b_f + 1 - b_f) \mu, (b_f + 1 - b_f) \Sigma) \\ &\sim \mathcal{N}_x (\mu, \Sigma) \\ \end{aligned}\]

이다. 즉, \(\hat{z}_x\)는 $z_x^{k,i}$와 동일한 표현 분포에 존재한다.

---

MeD에서는 \(\hat{z}_x = G_\theta^\mathcal{X} (\hat{z}_x^k)\)이므로 목적 함수는 다음과 같다.

\[\begin{equation} \underset{\theta, \rho, \psi}{\arg \min} \mathcal{L}^\mathcal{M} = \lambda \| \hat{z}_x - \textrm{Mix}_p (y_1^k, y_2^k) \| \end{equation}\]

여기서 $\lambda$는 가중치 파라미터이며, 타겟은 $y_1^k$와 $y_2^k$가 혼합된 버전을 사용한다.

Experiments

저자들은 DnCNN의 global residual connection이 feature 분리에 적합하지 않기 때문에 DnCNN 대신에 Swin-Transformer (Swin-T)를 통합하였다. 그럼에도 불구하고 Swin-T가 이미지 복원을 위해 디자인되지 않았기 때문에 이미지 전반에 걸쳐 로컬 의존성을 적용하기 위해 몇 가지를 수정하였다. 특히 Swin-T의 패치 임베딩 전과 패치 임베딩 해제 후에 각각 하나의 convolution layer를 추가한다. 이렇게 수정된 네트워크 backbone을 Swin-Tx라 부른다.

1. AWGN Noise Removal

다음은 CBSD68에서 합성 Gaussian noise에 대하여 여러 방법들과 정량적으로 비교한 표이다.

2. Generalisation on Unseen Noise Removal

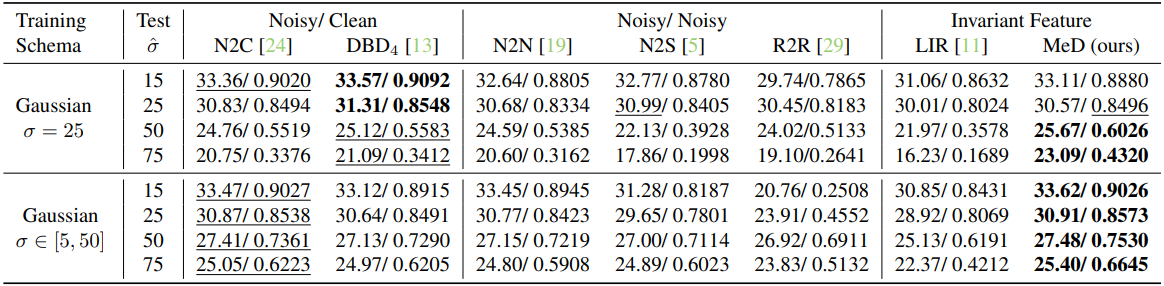
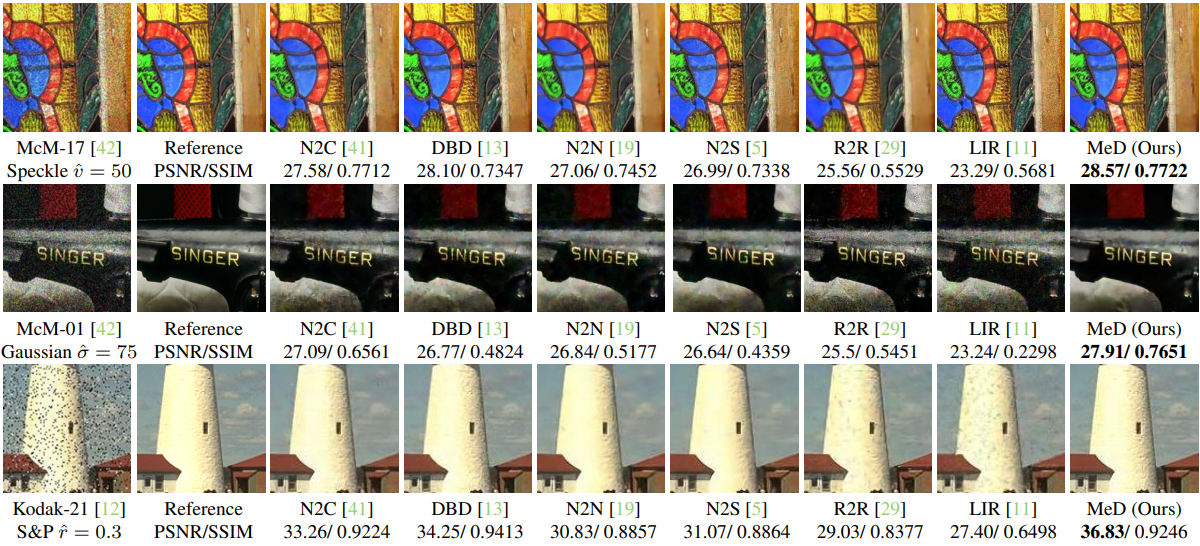
다음은 처음 보는 noise 유형에 대한 denoising 결과이다.

다음은 CBSD68에서의 일반화 성능이다.

3. Experiments on General Noise Pool

다음은 CBSD68에서의 Noise Pool을 분석한 표이다.

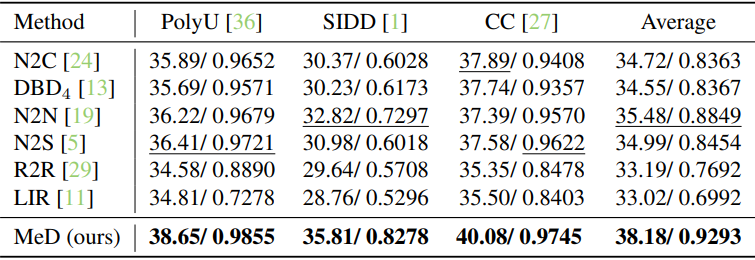
4. Real Noise Removal

다음은 SIDD에서의 실제 noise 제거 예시이다.

다음은 실제 noise 제거에 대하여 정량적으로 비교한 결과이다.

5. Expand to More Views

다음은 뷰의 개수에 따른 성능을 비교한 표이다.

6. More Application Exploration

다음은 Set5에서의 super-resolution 결과이다. (평균 PSNR/SSIM)

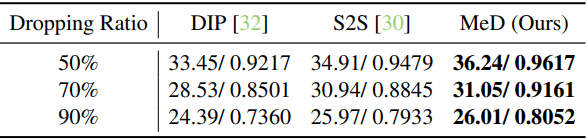
다음은 Set11에서의 인페인팅 결과이다. (평균 PSNR/SSIM)