[논문리뷰] Monte Carlo Tree Diffusion for System 2 Planning

ICML 2025 (Spotlight). [Paper]
Jaesik Yoon, Hyeonseo Cho, Doojin Baek, Yoshua Bengio, Sungjin Ahn
KAIST | SAP | Mila | New York University
11 Feb 2025

Introduction

Diffusion model은 최근 대규모 오프라인 데이터를 사용하여 궤적 분포를 모델링하여 복잡한 궤적을 생성할 수 있는 강력한 planning 방법으로 부상했다. 기존의 autoregressive planning 방법과 달리, Diffuser와 같은 diffusion 기반 planner는 일련의 denoising step을 거쳐 전체 궤적을 한 번에 생성하므로 forward dynamics model이 필요하지 않다. 이 접근법은 long-term dependency 모델링의 취약성 및 오차 누적과 같은 forward dynamics model의 주요 한계를 효과적으로 해결하여, 특히 horizon이 길거나 reward가 sparse한 planning task에 적합하다.

이러한 장점에도 불구하고, diffusion 기반 planner가 inference-time scalability를 통해 어떻게 planning 정확도를 효과적으로 향상시킬 수 있는지는 여전히 불확실하다. Denoising step 수를 늘리는 경우 이에 따른 성능 향상은 빠르게 정체되며, 여러 샘플을 사용하는 독립적인 무작위 검색은 다른 샘플의 정보를 활용하지 못하기 때문에 매우 비효율적이다. 또한, 이 프레임워크 내에서 exploration과 exploitation 사이의 trade-off를 효과적으로 관리하는 방법 또한 불확실하다.

이와 대조적으로, 널리 채택된 planning 방법인 Monte Carlo Tree Search (MCTS)는 강력한 inference-time scalability를 보여준다. MCTS는 반복적인 시뮬레이션을 활용하여 탐색적 피드백을 기반으로 결정을 개선하고 적응하며, 더 많은 계산이 할당됨에 따라 planning 정확도를 향상시키는 데 매우 효과적이다. 이러한 기능 덕분에 MCTS는 많은 시스템 2 추론 task에서 초석으로 자리 잡았다. 그러나 diffusion 기반 planner와 달리, MCTS는 트리 rollout을 위해 forward dynamics model에 의존하며, 이에 따른 한계를 그대로 이어받는다. 또한 discrete한 action space로 제한될 뿐만 아니라, 탐색 트리의 깊이와 너비 모두가 지나치게 커질 수 있다. 이는 특히 horizon이 길고 action space가 넓은 시나리오에서 상당한 계산을 필요로 한다.

본 논문은 Diffuser와 MCTS의 강점을 결합하여 그 한계를 극복하고 diffusion 기반 planning의 inference-time scalability를 향상시키는 Monte Carlo Tree Diffusion (MCTD)을 제안하였다. MCTD는 diffusion 기반 궤적 생성과 MCTS의 반복적 탐색 기능을 통합한 프레임워크이다.

MCTD는 세 가지 핵심 혁신을 기반으로 한다.

1. Denoising을 트리 기반 rollout 프로세스로 재구성하여 궤적 일관성을 유지하면서 semi-autoregressive causal planning을 가능하게 한다.
2. Exploration과 exploitation의 균형을 동적으로 맞추기 위해 meta-action으로 guidance level을 도입하여 diffusion 프레임워크 내에서 적응적이고 scalable한 궤적 개선을 보장한다.
3. Fast jumpy denoising을 시뮬레이션 메커니즘으로 사용하여 비용이 많이 드는 forward model rollout 없이 궤적 품질을 효율적으로 추정한다.

이를 통해 diffusion planning 내에서 MCTS의 4단계, 즉 Selection, Expansion, Simulation, Backpropagation을 구현하여 구조적 탐색과 생성 모델링을 효과적으로 연결하였다. MCTD는 long-horizon task에서 기존 방법보다 우수한 성능을 보이며, 탁월한 scalability와 품질을 달성하였다.

Preliminaries

Diffuser는 전체 궤적을 다음과 같은 행렬로 처리하여 long-horizon decision-making을 처리한다.

\[\begin{equation} \textbf{x} = \begin{bmatrix} s_0 & s_1 & \ldots & s_T \\ a_0 & a_1 & \ldots & a_T \end{bmatrix} \end{equation}\]

($s_t$와 $a_t$는 각각 시간 $t$에서의 state와 action)

그런 다음, diffusion process를 학습시켜 $\textbf{x}$의 샘플에서 noise 반복적으로 제거하여 궁극적으로 일관된 궤적을 생성한다. 실제로 이는 궤적 공간에 대해 denoiser \(p_\theta (\textbf{x})\)를 학습시켜 forward process를 역으로 수행하는 것과 같다. \(p_\theta\) 자체는 reward나 기타 task 목표를 인코딩하지 않으므로, Diffuser는 선택적으로 휴리스틱 또는 학습된 guidance function \(J_\phi (\textbf{x})\)를 통합한다. 이 함수는 부분적으로 denoise된 궤적의 return이나 value를 예측하여 샘플링 분포에 편향을 발생시킨다.

\[\begin{equation} \tilde{p}_\theta (\textbf{x}) \propto p_\theta (\textbf{x}) \exp (J_\phi (\textbf{x})) \end{equation}\]

따라서 각 denoising step에서 \(J_\phi\)의 gradient 정보는 모델을 오프라인 데이터에서 학습한 것처럼 실행 가능하고 return과 관련하여 유망해 보이는 궤적으로 밀어붙인다. 이는 이미지 diffuser의 classifier guidance와 유사한 방식이다.

Diffusion Forcing는 $\textbf{x}$의 tokenization을 허용함으로써 Diffuser를 확장하였다. 이 tokenization을 통해 각 토큰의 noise level을 다르게 하여 불확실성이 높은 구간의 부분적인 denoising이 가능하며, 전체 궤적에 걸쳐 noise가 완전히 없도록 전환할 필요가 없다. 이러한 토큰 수준 제어는 특히 long-horizon planning 문제와 같이 인과적 일관성이 요구되는 영역에서 유용하다.

Monte Carlo Tree Diffusion

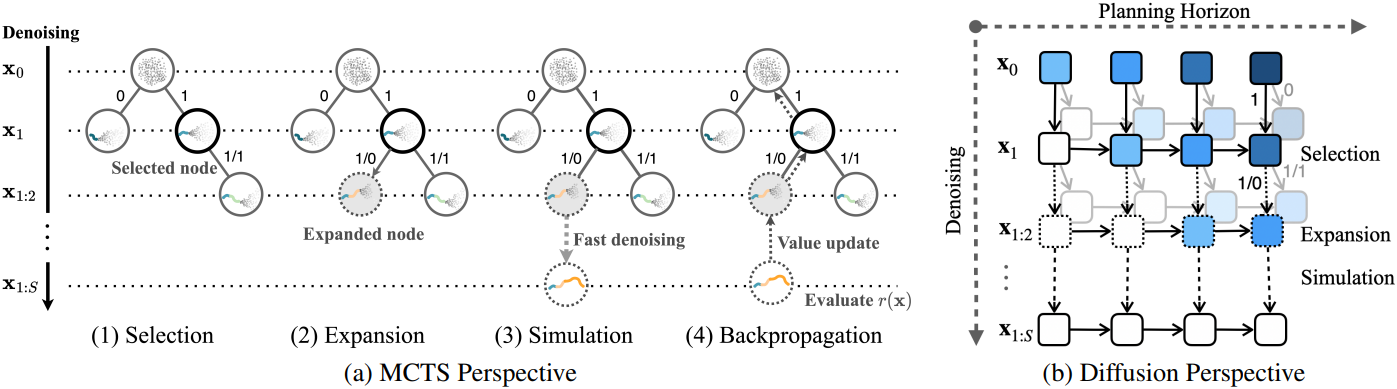
1. Denoising as Tree-Rollout

기존 MCTS는 개별 state를 기반으로 작동하기 때문에 탐색 트리가 깊어지고 scalability 측면에서 상당한 어려움을 겪는다. 트리의 각 노드가 하나의 state를 나타내기 때문에 트리의 깊이는 planning horizon에 따라 선형적으로 증가하여 탐색 공간이 기하급수적으로 증가한다. 또한, diffusion 기반 planner와 같이 전체 궤적을 한 번에 다루지 못한다. 반면, Diffuser는 exploration과 exploitation의 균형을 효과적으로 유지하는 트리 구조를 제공하지 않는다.

이 문제를 해결하기 위해, 먼저 Diffusion Forcing의 semi-autoregressive denoising process를 tree-rollout으로 사용한다. 구체적으로, 전체 궤적 \(\textbf{x} = (x_1, \ldots, x_N)\)을 $S$개의 subplan \(\textbf{x} = (\textbf{x}_1, \ldots, \textbf{x}_S)\)으로 분할한다. 모든 subplan이 동일한 denoising schedule을 공유하는 Diffuser와 달리, 각 subplan에 독립적인 denoising schedule을 할당할 수 있도록 한다. 이전 subplan에는 더 빠른 denoising을 적용하고 이후 subplan에는 더 denoising을 적용함으로써, 프로세스는 사실상 인과적이고 semi-autoregressive가 된다. 이를 통해 denoising process는 이미 결정된 과거를 기반으로 미래를 결정할 수 있다. 결과적으로, Diffuser의 글로벌하게 일관되고 한 번에 생성하는 이점을 유지하면서 denoising process를 다음과 같이 근사한다.

\[\begin{equation} p(\textbf{x}) \approx \prod_{s=1}^S p (\textbf{x}_s \vert \textbf{x}_{1:s-1}) \end{equation}\]

이 식은 autoregressive한 것처럼 보이지만 여전히 subplan 전체에서 noise level을 제어하여 단일 denoising process로 실행된다다.

MCTD에서는 각 subplan \(\textbf{x}_s\)가 개별 state $x_n$ 대신에 탐색 트리의 노드로 처리된다. 이를 통해 트리가 더 높은 수준의 추상화에서 작동하여 효율성과 scalability를 향상시킨다. 전체 계획 $\textbf{x}$의 denoising은 Diffuser의 단일 denoising process를 통해 이러한 노드 시퀀스를 rollout하는 것으로 볼 수 있다. $S \ll N$이므로 트리 깊이는 MCTS보다 훨씬 작아진다 (ex. $S = 5$, $N = 500$).

2. Guidance Levels as Meta-Actions

MCTS의 경우, 넓은 action space에서 트리를 구성하고 탐색하는 것은 계산적으로 비용이 많이 들며, continuous한 action space에서는 근본적으로 실용적이지 않다. 이 문제를 해결하기 위해 MCTD에서는 meta-action의 관점에서 exploration과 exploitation 사이의 trade-off를 재정의하는 새로운 접근법을 도입하였다. 본 논문에서는 denoising process에서 적용되는 guidance level로 meta-action을 구현하였다.

단순하게 GUIDE와 NO_GUIDE라는 두 가지 guidance level을 고려해 보자. Prior distribution $p(\textbf{x})$에서 샘플링하는 것, 즉 표준 diffusion 샘플러를 사용하는 것은 어떤 목표도 달성하려고 시도하지 않고 오프라인 데이터에 포함된 prior를 모방하기 때문에 exploration을 나타낸다. 따라서 이를 NO_GUIDE에 대응시킨다. 반대로, goal-directed distribution \(p_g(\textbf{x})\)에서 샘플링하는 것, 예를 들어 classifier-guided diffusion을 사용하는 것은 exploitation을 나타내므로 GUIDE가 할당된다. 이는 reward function \(r_g(\textbf{x})\)로 정의된 특정 goal을 달성하도록 샘플링 프로세스를 조정한다.

다음으로, meta-action의 개념을 tree-rollout denoising process와 통합한다. 이를 위해, 각 subplan \(\textbf{x}_s\)에 guidance meta-action \(g_s \in \{\textrm{GUIDE}, \textrm{NO_GUIDE}\}\)를 할당하는 guidance schedule $\textbf{g} = (g_1, \ldots, g_S)$를 도입한다. Guidance를 선택하지 않으면 subplan은 \(p(\textbf{x}_s \vert \textbf{x}_{1:s-1})\)에서 샘플링되고, guidance가 있는 subplan은 \(p_g(\textbf{x}_s \vert \textbf{x}_{1:s-1})\)에서 샘플링된다. 이를 통해 각 subplan에 guidance level을 독립적으로 할당할 수 있다.

Guidance schedule $\textbf{g}$를 동적으로 조정함으로써 단일 denoising process 내 subplan 수준에서 exploration과 exploitation의 균형을 이룰 수 있다. 확장된 tree-rollout denoising process는 다음과 같은 효과를 낸다.

\[\begin{equation} p (\textbf{x} \vert \textbf{g}) \approx \prod_{s=1}^S p (\textbf{x}_s \vert \textbf{x}_{1:s-1}, g_s) \end{equation}\]

결과적으로 이 접근 방식은 복잡하거나 continuous한 action space에서도 효율적이고 scalable한 planning을 가능하게 한다.

3. Jumpy Denoising as Fast Simulation

MCTS에서 계획 평가가 가능한 리프 노드에서 멀리 떨어진 노드를 평가하는 것은 매우 중요한 요구 사항이다. MCTD에서는 DDIM 기반의 fast jumpy denoising process를 사용하여 시뮬레이션을 구현한다. 구체적으로, tree-rollout denoising process가 $s$번째 subplan까지 진행되면, 나머지 step은 $C$ step씩 건너뛰어 빠르게 noise를 제거한다.

\[\begin{equation} \tilde{\textbf{x}}_{s+1:S} \sim p (\textbf{x}_{s+1:S} \vert \textbf{x}_{1:s}, \textbf{g}) \end{equation}\]

이렇게 하면 전체 궤적 \(\tilde{\textbf{x}} = (\textbf{x}_{1:s}, \tilde{\textbf{x}}_{s+1:S})\)가 생성되고, 이는 reward function \(r(\tilde{\textbf{x}})\)를 사용하여 평가된다. 이 빠른 denoising process는 더 큰 근사 오차를 유발할 수 있지만, 계산 효율이 매우 높아 MCTD의 시뮬레이션 단계에 적합하다.

4. The Four Steps of an MCTD Round

위 설명을 바탕으로, MCTS의 네 가지 기존 단계, 즉 Selection, Expansion, Simulation, Backpropagation을 구현할 수 있다.

Selection

Selection 단계는 루트 노드에서 리프 노드 또는 부분적으로 확장된 노드까지 트리를 순회하는 과정이다. 각 단계에서 UCB와 같은 선택 기준에 따라 자식 노드가 선택된다. 이 단계에서는 계산량이 많은 denoising이 필요하지 않고, 기존 트리 구조를 순회한다. MCTS와 달리, MCTD 노드는 시간적으로 확장된 state에 대응하여 더 높은 수준의 추론을 가능하게 하고 트리 깊이를 줄여 scalability를 향상시킨다. Guidance schedule $\textbf{g}$는 이 단계에서 UCB에 의해 동적으로 조정되어 exploration과 exploitation의 균형을 맞춘다.

Expansion

리프 노드 또는 부분적으로 확장된 노드가 선택되면 Expansion 단계에서는 현재 부분적으로 denoise된 궤적을 확장하여 새로운 자식 노드를 생성한다. 각 자식 노드는 diffusion model을 사용하여 생성된 새로운 subplan에 해당한다. Meta-action $g_s$에 따라 subplan은 \(p(\textbf{x}_s \vert \textbf{x}_{1:s-1})\) 또는 \(p_g(\textbf{x}_s \vert \textbf{x}_{1:s-1})\)에서 샘플링된다. 새로 생성된 노드는 현재 궤적의 확장으로 트리에 추가된다.

중요한 점은 guidance level이 바이너리일 필요는 없다는 것이다. 예를 들어, meta-action을 {ZERO, LOW, MEDIUM, HIGH}와 같은 여러 guidance level로 일반화하여 exploration과 exploitation 간의 균형을 더욱 세밀하게 제어할 수 있다.

Simulation

Simulation 단계는 fast jumpy denoising을 통해 구현된다. 노드가 확장되면, 빠른 denoising을 사용하여 나머지 궤적을 빠르게 완료한다. 그 결과로 생성된 계획 $\textbf{x}$는 plan evaluator $r(\tilde{\textbf{x}})$로 평가된다.

Backpropagation

Simulation 단계 후, 전체 계획을 평가하여 얻은 reward는 트리를 통해 backpropagation되어 루트 노드까지의 경로에 있는 모든 부모 노드의 value 추정치를 업데이트한다. 이 과정은 guidance schedule도 업데이트하여 트리가 향후 iteration을 위해 exploration과 exploitation 균형을 동적으로 조정할 수 있도록 한다. 이를 통해 reward로 나타내어지는 유망한 경로의 우선순위를 정하는 동시에, 조기 수렴을 방지하기 위한 충분한 탐색이 유지된다.

Experiments

1. Maze Navigation with Point-Mass and Ant Robots

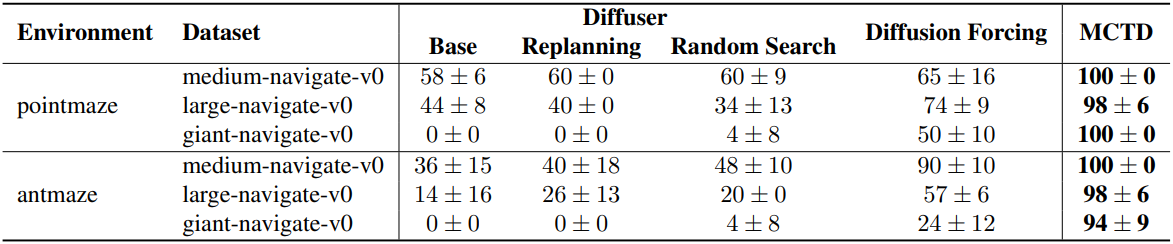
다음은 OGBench의 미로에 대한 결과이다.

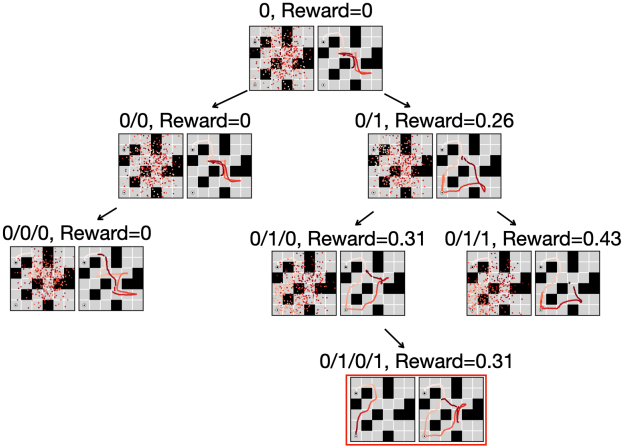
다음은 바이너리 meta-action에 대한 MCTD의 트리 탐색 과정을 시각화한 것이다.

다음은 생성된 계획과 실제 rollout을 비교한 결과이다.

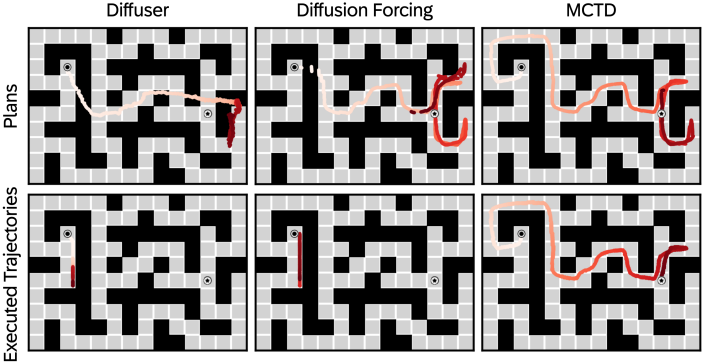
2. Robot Arm Cube Manipulation

OGBench의 multi-cube manipulation task의 경우 로봇 팔은 1~4개의 큐브를 특정 테이블 위치로 이동해야 한다. 큐브 수를 늘리면 planning horizon과 복잡성이 모두 커진다. 다음은 1~4개의 큐브에 대한 성공률을 비교한 결과이다.

MCTD는 적당한 성능 향상을 보이지만, 여러 물체가 관련될 경우 전체적인 계획 얽힘 현상이 발생한다. 이를 해결하기 위해 MCTD-Replanning은 주기적으로 다시 planning하여 각 큐브의 이동을 효과적으로 분리한다.

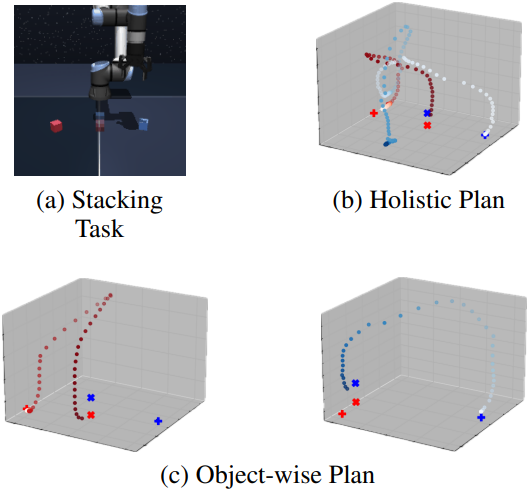
3. Visual Pointmaze

다음은 이미지 기반 planning을 평가하기 위한 visual pointmaze에서의 평가 결과이다.

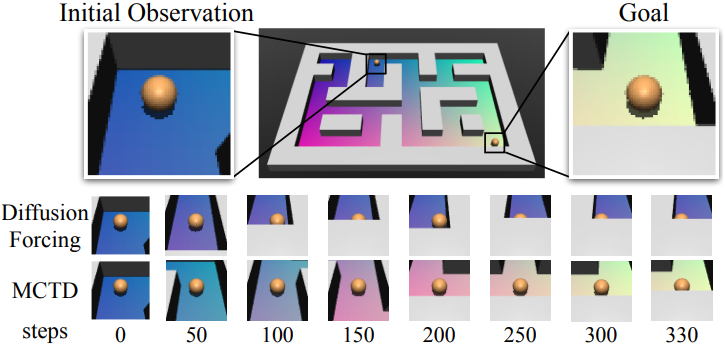
4. Inference-Time Scalability & Time Complexity

다음은 성공률과 실행 시간을 denoising step 수에 따라 비교한 결과이다.

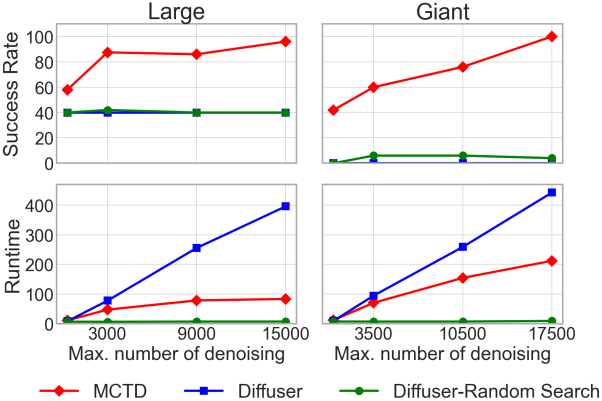
5. Ablation Studies

다음은 통계적 tree search가 exploration과 exploitation의 균형을 이루는 데 얼마나 효과적인지 평가하기 위해 greedy tree search를 평가한 결과이다. (PointMaze)

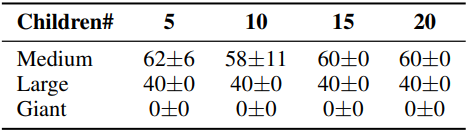
다음은 다양한 meta-action 세트에 대한 PointMaze 성공률을 비교한 결과이다.

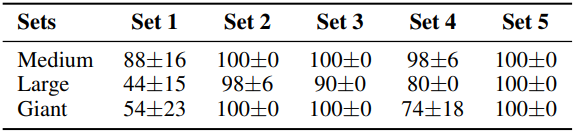
• Set 1: [0, 0.02, 0.05, 0.07, 0.1]
• Set 2: [0, 0.1, 0.5, 1, 2]
• Set 3: [0.5, 1, 2, 3, 4]
• Set 4: [4, 5, 6, 7, 8]
• Set 5: [0.1, 0.1, 1, 10, 100]

다음은 subplan 개수 $S$에 따른 PointMaze-Large 성공률을 비교한 결과이다.

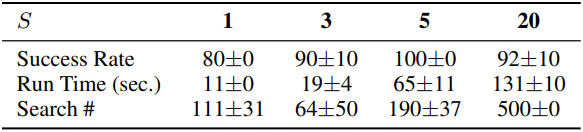
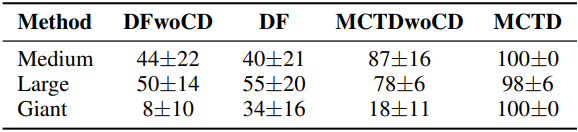
다음은 causal denoising (CD)과 트리 탐색에 대한 ablation 결과이다.