[논문리뷰] MaxFusion: Plug&Play Multi-Modal Generation in Text-to-Image Diffusion Models
ECCV 2024. [Paper] [Page] [Github]
Nithin Gopalakrishnan Nair, Jeya Maria Jose Valanarasu, Vishal M Patel
Johns Hopkins University | Stanford University
15 Apr 2024

Introduction
최근 test-to-image (T2I) diffusion model은 명령이나 스타일 기반 컨디셔닝과 같은 추가 제어 신호를 통합하여 더욱 확장되었다. 이를 통해 멀티태스킹 능력으로 보다 섬세한 제어를 가능하게 하여 사용자 선호도와 더욱 긴밀하게 일치하는 이미지를 생성할 수 있으며, 여러 조건을 모델에 동시에 제공할 수 있다.
그러나 여러 조건을 수용하도록 생성 모델을 학습하는 것은 주로 쌍을 이룬 멀티모달 데이터가 필요하기 때문에 상당한 과제를 안겨준다. 게다가 멀티모달 학습에서 만족스러운 성능을 얻으려면 종종 긴 학습이 필요하다. Transfer learning을 통해 대규모 T2I 모델을 더 작은 데이터셋으로 fine-tuning할 수 있다. 하지만, 이 과정에서 고정된 초기 조건과 데이터 선택에 의존하게 되며, 모델이 기존에 습득한 지식을 잃는 catastrophic forgetting 문제가 발생할 수 있다.
ControlNet과 T2I-Adapter는 diffusion model에 대한 추가 공간적 컨디셔닝을 포함하기 위해 task별 학습 가능한 파라미터를 도입하여 이 문제를 해결했다. 두 방법 모두 구조적 컨디셔닝을 잘 만족하는 인상적인 이미지 합성 품질을 보여주었다. 그러나 두 방법 모두 여러 task에 적용하려면 처음부터 학습하거나 여러 어댑터의 중간 출력에서 수동으로 파라미터를 조정해야 하며, 이는 컴퓨팅 시간과 메모리가 크게 증가한다. 따라서 여러 조건을 충족하는 이미지 및 동영상을 합성하는 것은 여전히 어려운 일이다.
다중 컨디셔닝을 위한 최근 연구인 UniControl은 다양한 모달리티에서 대규모 큐레이팅된 데이터로 생성 모델을 학습시켰다. 멀티태스킹 기반 학습 패러다임을 통해 UniControl은 ControlNet보다 더 나은 성능을 달성했다. 그러나 새로운 컨디셔닝 task를 추가하기 위해 모델을 재학습하여 새로운 task의 데이터뿐만 아니라 이전 모든 task의 데이터도 통합해야 한다는 한계점이 있다. 이를 scaling issue라고 하며, 사전 학습된 모델에 추가 task를 통합할 때 학습 복잡도가 증가하는 것을 의미한다. 본 논문은 다음과 같은 질문을 다룬다.
하나의 diffusion model이 재학습 없이 여러 다양한 task에 걸쳐 효율적으로 확장될 수 있도록 할 수 있는가?

본 논문에서는 별개의 단일 task 모델을 활용하는 새로운 feature 융합 방식을 활용한 학습이 필요 없는 솔루션 제안하였다. 저자들은 diffusion model의 여러 레이어에 걸친 feature variance map에서 파생된 feature 융합 기준을 설정하였으며, T2I 모델을 동시에 여러 task로 확장할 수 있는 간단하고 효율적인 feature 융합 알고리즘인 MaxFusion을 제안하였다. 따라서 T2I 모델에 zero-shot 멀티모달 생성 능력을 제공하였다.
Method
1. Unlocking Incremental Task Addition
ControlNet은 다양한 유형의 입력을 처리하도록 설계된 전용 레이어를 사용하여 구조적 컨디셔닝을 수행하여 다양한 입력 조건을 처리할 수 있다. 이러한 레이어에서 입력을 처리하면 diffusion UNet 모델의 첫 번째 레이어의 feature와 융합된다. 따라서 ControlNet의 학습 프로세스 중에 다양한 제어 모듈 입력 레이어 중 첫 번째 레이어의 가중치가 이미지의 latent space에 모달리티를 정렬한다는 결론을 내릴 수 있다. 그러므로 블록에 대한 입력은 diffusion UNet의 입력과 유사한 도메인으로 변환된다. 다양한 모달리티에 대한 ControlNet은 서로 다른 입력 모달리티를 처리하기 때문에 이러한 입력 처리 블록은 별도로 유지되어야 한다.
먼저 두 가지 중요한 질문을 살펴본다.
- 두 가지 서로 다른 입력과 동일한 backbone 아키텍처를 활용하는 경우, 모델에서 feature 위치를 어떻게 정렬하여 융합할 수 있는가?
- 두 가지 서로 다른 정렬된 feature가 있는 경우, 해당 feature 위치에서 조건을 적용하는 데 필요한 가장 관련성 있는 feature 벡터는 무엇인가?
2. Which Features are Aligned in Conditioned Diffusion Models?
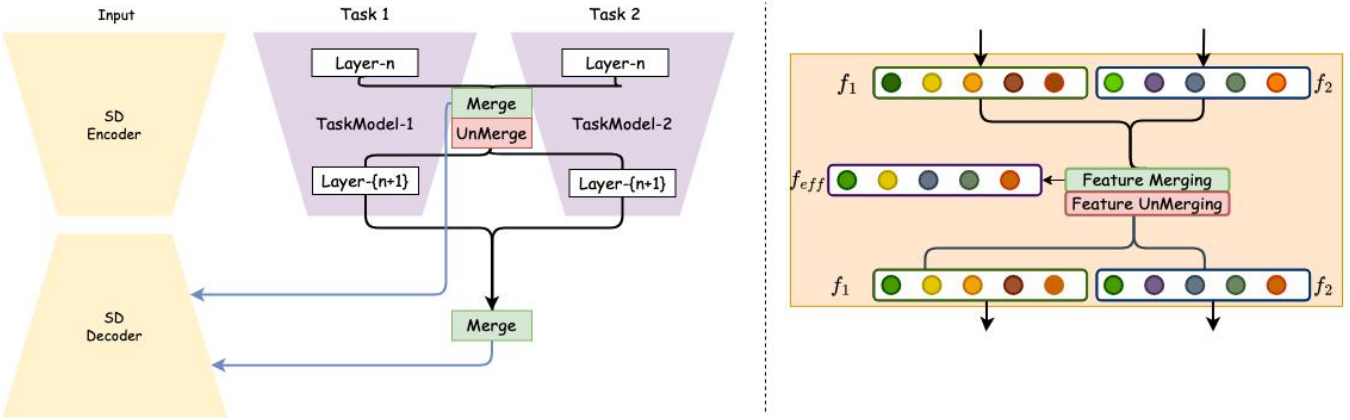
멀티모달 생성을 위한 feature 융합의 문제를 해결하기 위한 단순한 해결책은 모든 diffusion layer의 feature 평균을 계산하는 것이다. 그러나 feature가 정렬되지 않은 경우 이러한 융합은 비효율적인 컨디셔닝으로 이어진다. 이를 극복하기 위해 제어된 diffusion model의 모델 구조를 활용한다. 위 그림에서 볼 수 있듯이 중간 레이어 출력은 T2I 모델의 특정 레이어에 추가된다.
관찰 1. Stable Diffusion에서 동일한 공간적 위치에 추가된 다양한 모듈의 feature는 정렬된다.
3. Expressiveness of Control Modules
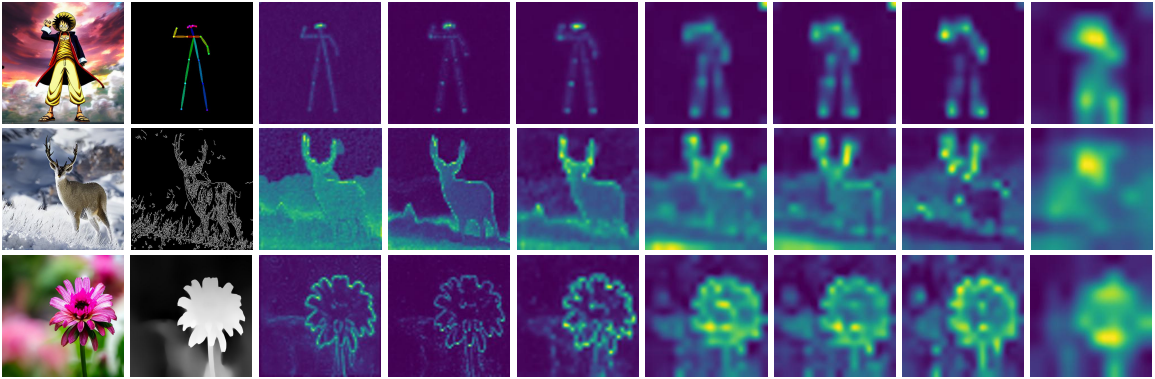
동일한 공간적 위치에서 두 가지 중에서 가장 적합한 feature를 선택하여 융합하는 것은 상당한 어려움을 안겨준다. 여러 모델의 중간 feature를 효과적으로 병합하려면 해당 특정 위치에서 조건의 강도나 표현력을 정량화하는 지표를 사용하는 것이 필수적이다. 네트워크는 해당 특정 위치에 가장 중요한 정보를 제공하는 조건을 식별하고 우선시해야 한다. 저자들은 간단하면서도 효과적인 관찰 결과를 얻었다.
관찰 2. Diffusion model에 제공된 조건의 표현력은 모델의 중간 레이어의 variance map을 사용하여 정량화될 수 있다.
저자들은 이를 입증하기 위해 위 그림에 나와 있는 것과 같이 동일한 이미지, noise, 텍스트 프롬프트에서 비롯된 다양한 제어 신호의 variance map을 조사하였다. Variance map은 특정 조건과 관련된 영역에서 더 높은 활성화를 보여주며, variance map이 각 영역에 필요한 컨디셔닝 강도의 척도로 사용될 수 있음을 시사한다. 따라서 모든 공간적 위치에서 각 조건의 중요도는 해당 위치에서 variance map의 활성화 수준으로 근사할 수 있다. 이 접근 방식은 각 조건의 상대적 중요도를 측정하는 신뢰할 수 있는 수단을 제공하여 보다 정보에 입각한 feature 선택을 가능하게 한다.
4. MaxFusion
먼저 두 개의 독립적인 모달리티를 융합하는 시나리오를 살펴보자. ControlNet 블록이 서로 다른 모달리티 $M_1$, $M_2$를 처리하도록 하자. 이러한 모달리티를 결합하는 기본적인 접근 방식은 단순히 평균을 계산하는 것이다.
\[\begin{equation} f_\textrm{avg} = \frac{f_1 + f_2}{2} \end{equation}\]그러나 이러한 단순한 융합 방법은 문제점이 존재한다. 예를 들어, 왼쪽 절반에는 깊이 정보만 있고 오른쪽 절반에는 모서리가 있는 이미지를 생각해보자. 위의 방식은 각 feature를 동등하게 평균화하여 각 feature의 중요도를 희석한다.
이상적인 방식은 공간적으로 조정되어 주어진 위치 $(j, k)$에서 모달리티 입력 값에 더 많은 가중치를 부여하는 것이다. 이를 위해 각 공간적 위치에서 feature의 상관 관계를 평가한다. 상관 관계가 높은 feature의 경우 다음과 같은 가중 합산 방식을 채택한다.
\[\begin{equation} f_\textrm{eff}^{(j,k)} = \frac{f_1^{(j,k)} + f_2^{(j,k)}}{2}, \quad \textrm{if} \; \rho^{(j,k)} > \delta \end{equation}\]여기서 $\delta$는 미리 정의된 threshold이고 \(\rho^{(j,k)}\)는 각 공간 위치에서 \(f_1^{(j,k)}\)과 \(f_2^{(j,k)}\) 사이의 상관관계 값을 나타내며 다음과 같이 정의된다.
\[\begin{equation} \rho^{(j,k)} = \frac{f_1^{(j,k)} \cdot f_2^{(j,k)}}{\vert f_1^{(j,k)} \vert \cdot \vert f_2^{(j,k)} \vert} \end{equation}\]상관관계가 threshold 아래로 떨어지면 가장 공간적 정보가 많은 모달리티를 우선시한다. 이 우선순위는 해당 위치의 feature의 분산에 의해 결정된다. 분산 값이 다른 모달리티 간의 공정성을 보장하기 위해 공간적 위치에 걸쳐 표준 편차 값을 정규화하여 상대적인 표준 편차를 측정한다.
\[\begin{equation} \bar{\sigma}_i^{(j,k)} = \frac{\sigma_i^{(j,k)}}{\sum_{(j,k)} \sigma_i^{(j,k)}} \end{equation}\]따라서 상관관계가 threshold 아래에 있는 경우 집계된 feature를 채널 표준 편차가 가장 높은 feature로 정의한다.
\[\begin{equation} f_\textrm{eff}^{(j,k)} = f_i^{(j,k)}, \; i = \max_i \hat{\sigma}_i^{(j,k)}, \quad \textrm{if} \; \rho^{(j,k)} < \delta \end{equation}\]이를 통해 더 관련성 있는 조건을 자동으로 선택하여 효과적인 컨디셔닝을 제공한다.
5. InterModel Unmerging
InterModel 병합 단계에서는 상관관계 값이 사전 정의된 threshold를 초과하는지 평가한다. 이 기준을 충족하지 않는 각 공간적 위치에 대해 해당 위치에서 전달되는 feature가 속했던 동일한 인덱스에 해당하고 최대 분산을 갖는지 확인한다. 최대 분산을 가지고 있는 경우 이를 그대로 전달하고, 그렇지 않은 경우 병합하기 전에 feature 벡터를 다시 조정하여 동일한 표준 편차를 갖도록 한다.
\[\begin{aligned} f_i^{(j,k)} &= \begin{cases} f_i^{(j,k)} & \quad i = \max_i \hat{\sigma}_i^{(j,k)} \\ (\sigma_i^{(j,k)} / \sigma_\textrm{max}^{(j,k)}) f_\textrm{max}^{(j,k)} & \quad \textrm{otherwise} \end{cases} \\ f_\textrm{max}^{(j,k)} &= f_i^{(j,k)}, \; i = \max_i \sigma_i^{(j,k)} \end{aligned}\]위와 같은 분산 재정규화는 \(f_\textrm{eff}\) 추정 중에 감소된 영역을 재활성화한다. 이러한 feature 강도의 소멸 효과는 무효화되고 재조정되어 성능이 향상된다. 전체 알고리즘은 Algorithm 1과 같다.

Experiments
- 데이터셋: COCO
- 컨디셔닝: depth map, segmentation mask, HED, canny edge
- 구현 디테일
- T2I 모델: Stable Diffusion
- task 모델: ControlNet, T2I-Adapter
- diffusion step: 50
- threshold: 0.7
- GPU: NVIDIA A5000 GPU 1개
1. Contradictory Conditions
다음은 모순되는 조건들에 대한 생성 결과들을 비교한 것이다.

2. Complementary Conditions
다음은 상호 보완적인 조건들에 대한 생성 결과들을 비교한 것이다.

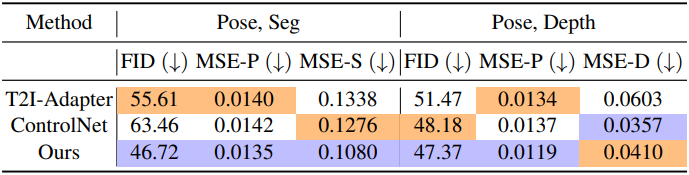
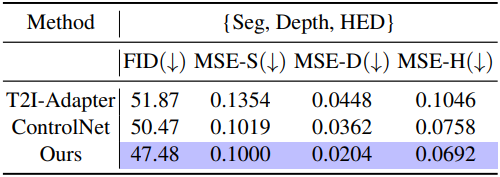
다음은 상호 보완적인 조건들에 대한 생성 결과들을 정량적으로 비교한 표이다. (각각 Seg + Depth, Hed + Depth, Hed + Seg)

3. Discussions
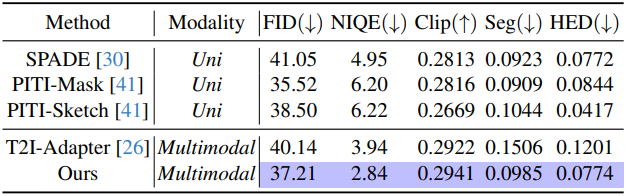
다음은 스타일을 모달리티로 사용하였을 때의 생성 결과이다.

다음은 3개의 모달리티로 확장한 결과이다.

4. Ablation Studies
다음은 threshold에 대한 ablation 결과이다.
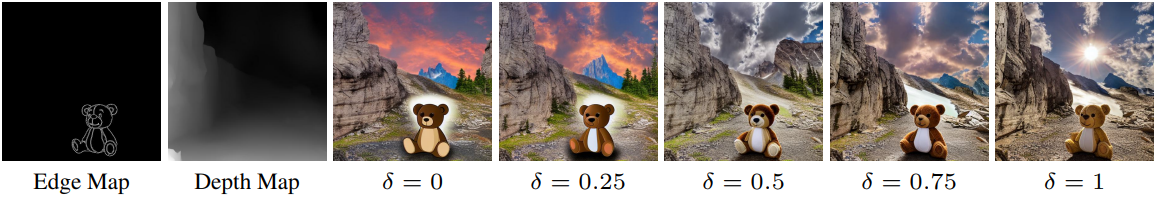
다음은 멀티모달 컨디셔닝에 대한 ablation 결과이다.
